Quantum Leaps in Optimization: A New Hybrid Approach

Author: Denis Avetisyan

Researchers have combined the strengths of quantum computing and classical algorithms to tackle complex integer linear programs, potentially unlocking faster and more efficient solutions.

The study demonstrates that incorporating a branch and bound approach-limiting iterations to 50 per node-into a variational quantum eigensolver consistently guides the optimization process closer to the optimum than relying solely on quantum approximate optimization, as evidenced by the reduced distance from the optimal cost with increasing queries to the quantum simulator.

This review details a novel hybrid branch and bound algorithm leveraging variational quantum optimization for improved performance in challenging optimization problems.

Despite the promise of quantum computing, practical applications to complex optimization problems remain challenging due to limitations in current quantum hardware. This paper introduces ‘A Quantum-Classical Hybrid Branch & Bound Algorithm’-a novel approach that integrates a variational quantum optimizer within a classical branch-and-bound framework for solving binary linear programs. By leveraging noisy quantum samples for problem reduction and classical approximations for bound calculation, the algorithm aims to enhance solution quality and reduce computational complexity. Will this hybrid strategy pave the way for more effective quantum-assisted solutions to real-world integer programming challenges?

The Illusion of Optimization: Why Everything Gets Complicated

The effective management of modern systems frequently hinges on the ability to solve complex optimization tasks. From determining the most efficient distribution of limited resources – be it financial capital, medical supplies, or energy – to orchestrating the intricate logistics of global supply chains and transportation networks, these challenges demand finding the best possible solution from a vast landscape of possibilities. These problems aren’t merely academic exercises; their solutions directly impact efficiency, cost, and even lives. Consider, for example, optimizing delivery routes to minimize fuel consumption or allocating bandwidth in a communication network to maximize data throughput – each scenario presents a unique, multifaceted optimization problem requiring sophisticated approaches to navigate the trade-offs between competing objectives and constraints.

The fundamental challenge in optimization lies in the rapid growth of computational demands as problem complexity increases. Classical approaches, notably exhaustive search, systematically evaluate every possible solution to identify the optimal one. While guaranteed to find the best answer, this method suffers from a combinatorial explosion; the number of possibilities grows factorially with the number of variables. For instance, a problem with just 20 variables could require evaluating over a million combinations. This quickly renders exhaustive search computationally intractable, even with powerful hardware. Consequently, scalability becomes a major limitation, and the quality of solutions diminishes as algorithms are forced to consider only a small fraction of the solution space, hindering their effectiveness in addressing real-world challenges involving numerous interacting factors.

While classical optimization methods struggle with complex problems, approximation algorithms present a trade-off between computational efficiency and solution quality. These algorithms prioritize speed, often achieving results in a reasonable timeframe even for large-scale challenges, but this comes at the cost of guaranteed optimality. Instead of finding the absolute best solution, they aim for a result that is “good enough” – within a predictable margin of error from the ideal outcome. This compromise can be problematic in critical applications, such as emergency response logistics or financial modeling, where even a small degree of suboptimality can translate into significant real-world consequences. The degree of acceptable error, therefore, must be carefully considered and balanced against the benefits of reduced computational time, necessitating a thorough understanding of the algorithm’s performance guarantees and potential limitations.

The branching algorithm systematically reduces a problem by solving a master problem, assigning variable values, propagating constraints, and pruning infeasible or non-promising subproblems based on calculated bounds.

Quantum Dreams and Classical Realities

Quantum optimization algorithms achieve potential speedups by utilizing the principles of superposition and entanglement. Superposition allows a quantum bit, or qubit, to represent 0, 1, or a combination of both simultaneously, enabling the algorithm to explore multiple potential solutions concurrently. Entanglement links the states of two or more qubits, meaning the state of one qubit instantly influences the others, facilitating correlations in the search process. This differs from classical optimization, where solutions are evaluated sequentially. By encoding a problem’s variables into qubits and leveraging these quantum phenomena, the algorithm effectively explores a vastly larger solution space than would be feasible for classical methods, potentially identifying optimal or near-optimal solutions more efficiently. The computational complexity scales with the number of qubits, but the potential for parallel exploration offers advantages for certain problem types.

Quantum Approximate Optimization Algorithm (QAOA) and variational Quantum Iterative Eigensolver Technology (varQITE) represent promising approaches to achieving computational speedups for optimization problems compared to classical algorithms. While theoretical analyses suggest potential advantages, particularly for certain problem structures, realizing these speedups in practice is currently hindered by several factors. These include the limited availability of large-scale, fault-tolerant quantum computers, the impact of noise on quantum computations, and the overhead associated with state preparation and measurement. Furthermore, the performance of these algorithms is highly problem-dependent, and determining the optimal parameters for QAOA and varQITE often requires significant computational resources – sometimes approaching the complexity of the classical problem itself. Current research focuses on mitigating these challenges through error correction techniques, improved quantum hardware, and the development of more efficient optimization strategies for parameter tuning.

Many quantum optimization algorithms, including Quantum Approximate Optimization Algorithm (QAOA) and Variational Quantum Eigensolver (VQE), necessitate the reformulation of target problems into specific mathematical structures for processing on quantum hardware. Commonly, these algorithms require problems to be expressed as Quadratic Unconstrained Binary Optimization (QUBO) or Ising Hamiltonian problems. A QUBO formulation represents the objective function as a quadratic polynomial of binary variables, while the Ising model describes interacting spins. This requirement for problem mapping can significantly limit the direct applicability of these algorithms; problems not easily convertible to QUBO or Ising formats may require substantial pre-processing or approximation, potentially introducing inaccuracies or negating any performance gains. The complexity of this mapping step, and the potential for increased problem size during conversion, must be considered when evaluating the feasibility of using quantum optimization for a given task.

Employing branch and bound with a 50-iteration limit per node (blue) significantly accelerates convergence to optimal cost (0) compared to using plain QAOA (red) alone.

QCBB: A Pragmatic Bridge Between Theory and Practice

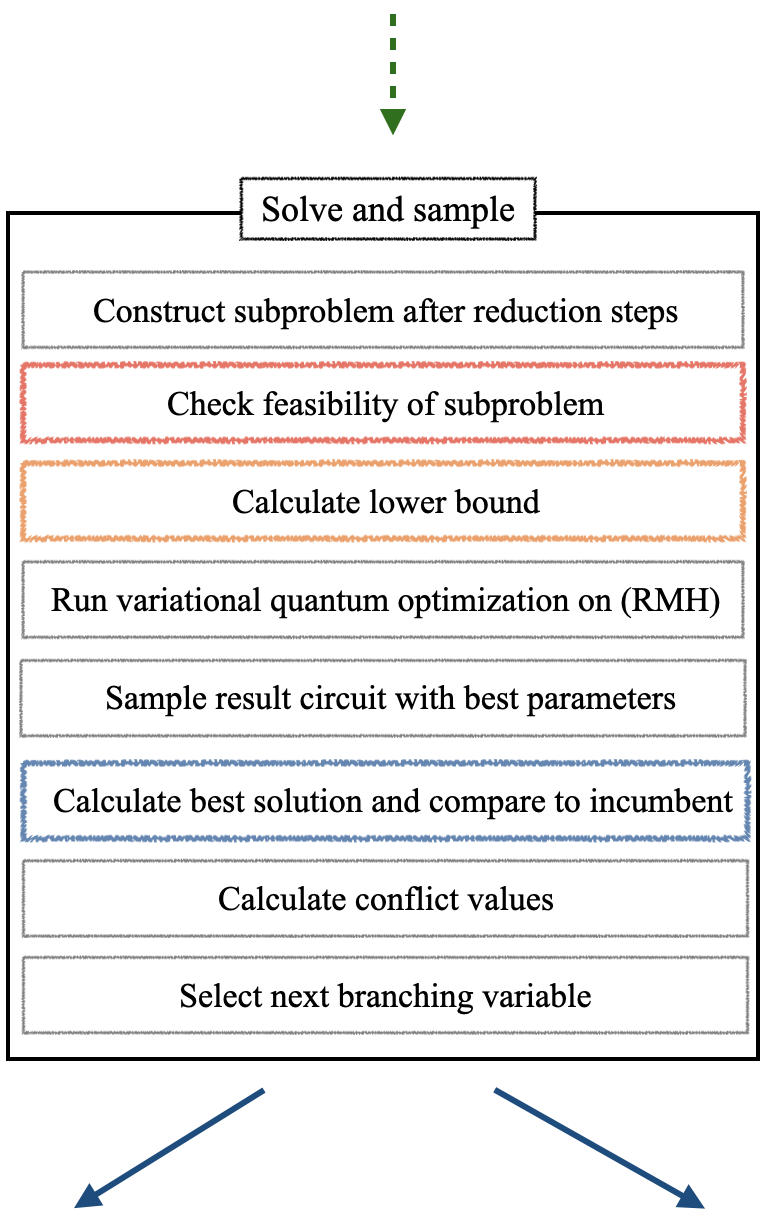
Quantum Conflict-Driven Branch and Bound (QCBB) represents a hybrid algorithmic approach that integrates the established framework of classical Branch and Bound with techniques from quantum optimization. Branch and Bound systematically explores a solution space by recursively dividing a problem into smaller subproblems, while quantum optimization, in this context, is leveraged to efficiently solve specific subproblems or evaluate the quality of potential solutions. QCBB aims to overcome limitations of both purely classical and purely quantum algorithms by strategically combining their strengths; the classical component manages the overall search process and decomposition, while the quantum component accelerates computationally intensive tasks within that framework. This synergy enables QCBB to potentially address complex optimization problems more effectively than either approach in isolation.

Quantum Conflict-Driven Branch and Bound (QCBB) employs Benders Decomposition to divide a complex optimization problem into a master problem and one or more subproblems, iteratively refining the solution. This decomposition allows for a more manageable problem size for the quantum solver. Simultaneously, Conflict-Driven Constraint Generation identifies and adds constraints based on infeasible solutions discovered during the Branch and Bound process. These generated constraints effectively prune the search space, directing the quantum optimization towards feasible and promising regions. The combined approach ensures that the quantum resources are focused on solving increasingly constrained and relevant subproblems, improving the overall efficiency of the algorithm and accelerating convergence to an optimal solution.

The QCBB algorithm incorporates a ConflictValue metric to dynamically prioritize quantum resource allocation. This metric quantifies the degree of constraint violation within a given subproblem, effectively identifying regions of the solution space that are both infeasible and contribute significantly to the overall problem difficulty. By assigning higher computational effort to subproblems with larger ConflictValue scores, QCBB directs the quantum optimization process toward areas most likely to yield improvements in the solution’s feasibility and objective function value. This targeted approach minimizes wasted quantum computations on unpromising regions, resulting in enhanced efficiency and faster convergence compared to uniform sampling or exploration of the solution space.

Experimental validation of the Quantum Conflict-Driven Branch and Bound (QCBB) algorithm indicates a key advantage in problem scaling: the number of many-body terms does not increase with each subproblem created during the decomposition process. This stability is coupled with observed convergence behavior; the difference between established upper and lower bounds diminishes as each node is evaluated within the Branch and Bound framework. Consequently, QCBB demonstrates a lower expected solution cost when benchmarked against plain Quantum Approximate Optimization Algorithm (QAOA) implementations for comparable problem instances. These results suggest QCBB effectively manages problem complexity and improves solution accuracy through iterative refinement of bounds.

Convergence analysis across sixteen problem instances demonstrates that both upper (blue) and lower (red) bounds progressively tighten with increasing node evaluations, ultimately approaching the known optimum (solid black line) while accounting for the cost of the worst feasible solution (dashed black lines) using a hybrid linear-logarithmic scale.

Beyond the Algorithm: Expanding QCBB’s Reach

The Quantum Combinatorial Black Box (QCBB) exhibits a unique structural flexibility, allowing for the seamless integration of advanced search algorithms like QuantumTreeSearch. This capability is particularly valuable when addressing optimization problems characterized by complex, tree-like solution spaces – scenarios where exhaustive search becomes computationally intractable. QuantumTreeSearch, layered onto the QCBB architecture, leverages quantum principles to navigate these intricate landscapes more efficiently, effectively pruning unpromising branches and accelerating the identification of optimal or near-optimal solutions. By systematically exploring possibilities within this tree structure, QCBB, enhanced by QuantumTreeSearch, demonstrates a significant potential for solving problems across fields like logistics, scheduling, and machine learning, where branching decision processes are prevalent.

The Quantum Combinatorial Binary Builder (QCBB) isn’t limited to a single approach; its core architecture is intentionally designed to integrate sophisticated decomposition methods, substantially enhancing its ability to handle increasingly complex problems. These techniques break down large optimization challenges into smaller, more manageable subproblems that can be tackled individually or concurrently. By strategically partitioning the original problem, QCBB minimizes the computational resources required for each step, leading to significant improvements in both scalability and overall performance. This modularity allows researchers to explore and incorporate state-of-the-art decomposition algorithms – such as those used in graph partitioning or constraint satisfaction – seamlessly into the QCBB framework, unlocking further potential for solving previously intractable optimization tasks.

Quantum Combinatorial Black Box (QCBB) doesn’t operate in a vacuum; its design intentionally builds upon the solid foundation of classical optimization algorithms. A prime example lies in its adaptation of the Goemans-Williamson algorithm for the MaxCut problem. This established technique, known for its use of semidefinite programming to find near-optimal cuts in a graph, provides QCBB with a robust starting point. However, QCBB then introduces quantum enhancements – leveraging quantum phenomena to potentially accelerate the search for solutions and improve the quality of the cut found. This hybrid approach allows QCBB to capitalize on decades of refinement in classical algorithms while simultaneously exploring the benefits quantum computing offers, potentially exceeding the performance limits of purely classical methods for certain problem instances and opening new avenues for tackling complex optimization challenges.

The Quantum Combinatorial Branch and Bound (QCBB) framework transcends the limitations of specialized algorithms by offering a broadly applicable approach to optimization. Its capacity to adapt to diverse problem structures-from logistics and finance to machine learning and materials science-stems from its foundational ability to explore complex solution spaces with both classical and quantum strategies. This versatility allows QCBB to address challenges where traditional methods falter, particularly those characterized by a vast number of possible combinations or intricate constraints. By seamlessly integrating with existing classical algorithms and benefiting from potential quantum speedups, QCBB isn’t merely a solution for specific problems; it represents a flexible platform poised to redefine optimization across numerous scientific and industrial disciplines, offering a pathway toward more efficient and innovative solutions.

Tree evaluation proceeds by pruning infeasible or bounded nodes (highlighted in red and orange) and potentially updating the best known solution (blue).

Towards Practical Quantum Advantage: The Road Ahead

The pursuit of quantum optimization hinges significantly on the continued refinement of Quantum Classical Batching and Batching (QCBB) alongside related hybrid algorithms. These approaches, which strategically interweave quantum computations with classical processing, offer a promising pathway to overcome the limitations of current quantum hardware. Further development focuses on maximizing the efficiency of this interplay-reducing the number of quantum resources required and minimizing the communication overhead between quantum and classical components. Researchers are actively exploring novel batching strategies and optimization techniques to enhance scalability and broaden the range of problems amenable to QCBB. Ultimately, these advancements are not merely about improving existing algorithms, but about building a robust framework capable of delivering a demonstrable quantum advantage for complex, real-world optimization challenges.

The successful implementation of quantum algorithms, particularly those leveraging hybrid quantum-classical approaches, hinges on a delicate balance between computational resources. Maximizing performance requires careful orchestration of tasks assigned to both quantum and classical processors; offloading computationally intensive, yet classically efficient, steps to conventional hardware minimizes the demands on limited and error-prone quantum resources. Conversely, leveraging the unique capabilities of quantum computation – such as superposition and entanglement – for tasks intractable for classical computers is paramount. Research focuses on intelligently partitioning problems, optimizing data transfer between systems, and developing error mitigation strategies tailored to the specific strengths and weaknesses of each component. This synergistic approach aims to reduce overall computational cost, enhance solution accuracy, and ultimately unlock the potential for quantum advantage by minimizing the overhead associated with both quantum execution and classical processing.

The practical scope of Quantum Combinatorial Black Box (QCBB) hinges on its adaptability to diverse problem structures, necessitating innovative approaches to problem formulation and decomposition. Researchers are actively investigating methods to recast complex challenges into forms more amenable to QCBB’s strengths, often involving the identification of substructures that can be efficiently tackled on quantum hardware. Crucially, strategies for decomposing large-scale problems into smaller, interconnected subproblems are being refined; this allows for a hybrid quantum-classical workflow where quantum processors focus on computationally intensive segments while classical algorithms manage overall coordination and integration. These decomposition techniques not only mitigate the limitations of current quantum hardware but also unlock the potential for QCBB to address previously intractable problems in fields like logistics, finance, and materials science, paving the way for tangible quantum advantage.

The promise of quantum computing extends beyond theoretical capabilities, and Quantum Combinatorial Black Box (QCBB) stands poised to deliver practical advantages across diverse sectors as both quantum hardware and algorithmic techniques mature. Anticipated improvements in qubit stability, coherence times, and connectivity will allow QCBB to tackle increasingly complex optimization problems currently intractable for classical computers. Simultaneously, refinements in algorithm design – including enhanced decomposition strategies and hybrid quantum-classical approaches – will minimize computational overhead and maximize the benefits gleaned from limited quantum resources. This convergence of hardware and software advancements suggests QCBB could revolutionize fields such as logistics, finance, materials science, and drug discovery, offering substantial gains in efficiency, accuracy, and innovation. The ability to efficiently explore vast solution spaces positions QCBB not merely as a futuristic technology, but as a potential catalyst for significant progress in a multitude of industries.

The pursuit of elegant solutions, as demonstrated by this hybrid quantum-classical approach to integer linear programming, invariably encounters the blunt reality of production environments. This work attempts to tame complexity through a blend of variational quantum optimization and branch and bound-a neat trick, if it survives first contact with actual data. As Paul Dirac once observed, “I have not the slightest idea of what I am doing.” The sentiment rings true; each layer of abstraction, each attempt to optimize, merely shifts the potential points of failure. The algorithm’s promise of reduced complexity feels less like a triumph of theory and more like a temporary reprieve before the inevitable emergence of new, unforeseen constraints. Tests, after all, are a form of faith, not certainty.

What’s Next?

The presented hybrid approach, while conceptually neat, merely shifts the burden of intractability. Solving an integer linear program rarely becomes ‘easy’ simply by introducing a variational quantum optimizer; it usually becomes a more expensive way to complicate everything. The immediate future will inevitably involve extensive empirical study – and not the kind presented in optimistic pre-prints. Production systems will expose the algorithm’s scaling limitations with a ruthlessness academic benchmarks often lack. Expect to see diminishing returns as problem size increases, and a proliferation of ad-hoc heuristics to manage the quantum optimizer’s quirks.

A crucial, and likely painful, area for future work lies in error mitigation. The algorithm’s sensitivity to noise-a characteristic shared by nearly all near-term quantum algorithms-will require robust techniques. Furthermore, the interplay between the quantum and classical components demands deeper investigation. How does the conflict-driven constraint generation truly ‘guide’ the quantum search, or is it simply an expensive bookkeeping exercise? If code looks perfect, no one has deployed it yet.

Ultimately, the success of such hybrid methods hinges not on theoretical elegance, but on pragmatic engineering. The field will likely see a move toward specialized hardware tailored to this specific algorithm, acknowledging that general-purpose quantum computers remain a distant prospect. This work is, at best, a step toward a potentially useful, but certainly complex, tool. And like all tools, its value will be determined by what breaks first.

Original article: https://arxiv.org/pdf/2511.19501.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/