Squeezing Light for Quantum Advantage

by

Author: Denis Avetisyan

Researchers have developed a versatile technique for generating complex quantum states of light, paving the way for more powerful quantum information processing.

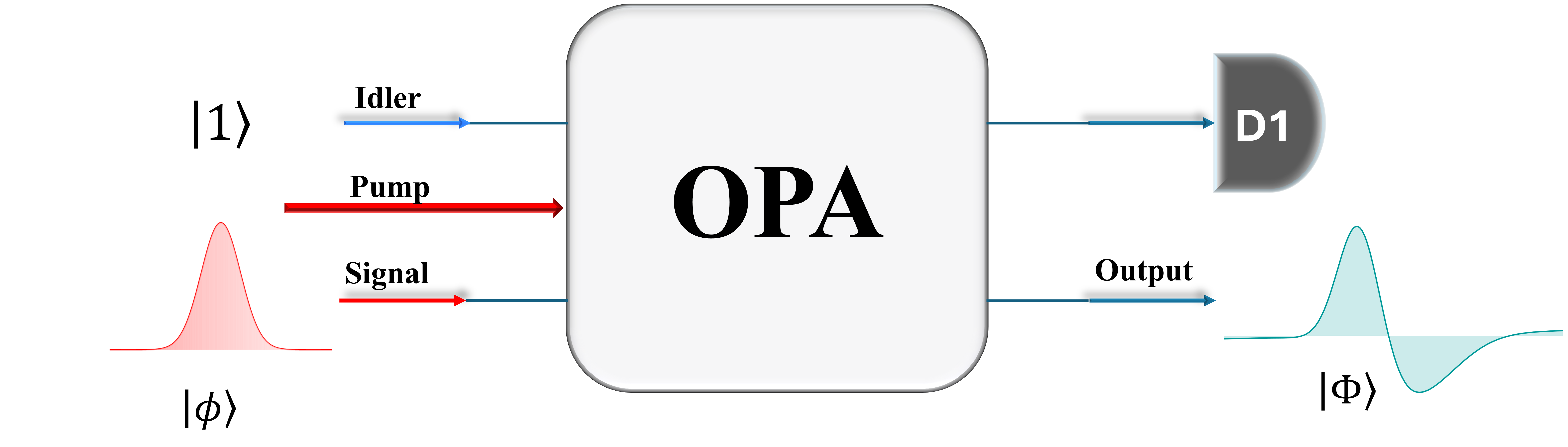
Non-Gaussian quantum states, including squeezed vacuum and small-amplitude Schrödinger cat states, are generated through optical parametric amplification; injecting these states into the signal mode alongside a single photon in the idler mode allows heralded generation of a non-Gaussian state at the signal output, with the amplifier gain serving as a key control parameter for state characteristics.
Non-Gaussian quantum states, including squeezed vacuum and small-amplitude Schrödinger cat states, are generated through optical parametric amplification; injecting these states into the signal mode alongside a single photon in the idler mode allows heralded generation of a non-Gaussian state at the signal output, with the amplifier gain serving as a key control parameter for state characteristics.

A generalized heralded Optical Parametric Amplifier protocol enables high-fidelity generation of non-Gaussian states, including squeezed and photon number states, from squeezed vacuum and small-amplitude squeezed state inputs.

Generating complex non-Gaussian quantum states-essential for advanced quantum technologies-has traditionally relied on specialized and often cumbersome experimental setups. This limitation is addressed in ‘Generalized Heralded Generation of Non-Gaussian States Using an Optical Parametric Amplifier’, which introduces a versatile heralded protocol capable of deterministically creating high-fidelity non-Gaussian states from diverse inputs. By leveraging an optical parametric amplifier, the researchers demonstrate the generation of large-amplitude squeezed states and the amplification of initial non-Gaussianity, effectively distilling key quantum resources. Could this integrated approach pave the way for more practical and scalable quantum information processing platforms?

The Imperative of Non-Classical States in Quantum Advancement

The burgeoning field of quantum technology – encompassing advancements in computation, communication, and sensing – demands an unprecedented degree of control over the states of quantum systems. However, classical physics, which accurately describes much of the macroscopic world, proves fundamentally inadequate when attempting to model these delicate quantum phenomena. While classical descriptions can approximate certain behaviors, they fail to capture the essential features of quantum states like superposition and entanglement – properties critical for achieving exponential speedups in computation or secure communication protocols. The limitations stem from the fact that classical physics treats properties as definite values, whereas quantum mechanics describes them using probabilities and wave functions, necessitating a fundamentally different mathematical framework to accurately predict and manipulate quantum systems. Consequently, researchers are continually developing new theoretical tools and experimental techniques to move beyond classical intuition and harness the full potential of quantum mechanics.

Quantum information processing often relies on states of light to encode and manipulate data, and Gaussian states – those fully described by classical probability distributions – have historically served as a convenient starting point. However, these states possess limitations when applied to more sophisticated tasks. While adept at representing certain quantum phenomena, Gaussian states are fundamentally incapable of exhibiting the quantum properties – such as entanglement beyond specific bounds or the presence of non-classical correlations like Einstein-Podolsky-Rosen steering – necessary for achieving significant advantages in computation or communication. Advanced protocols, including fault-tolerant quantum computing and secure quantum key distribution, demand the ability to create and control more complex, non-Gaussian states that can surpass the capabilities offered by their classical counterparts. The inability of Gaussian states to fully capture these features represents a key obstacle in realizing the full potential of quantum technologies, necessitating research into novel methods for generating and manipulating light in non-classical ways.

The pursuit of robust and scalable quantum technologies hinges on the ability to create and reliably measure states of light that defy classical intuition. While Gaussian states – those describable by normal probability distributions – have served as a foundational tool, they represent only a limited subset of possible quantum states and restrict the performance of many quantum algorithms. Truly unlocking the power of quantum computation, sensing, and communication requires venturing beyond these Gaussian limitations to engineer and thoroughly characterize non-classical, or non-Gaussian, states – those exhibiting squeezed light, entanglement, and discrete superposition. These states enable protocols impossible with classical light, offering enhanced security in quantum key distribution, increased precision in quantum metrology, and the potential for exponential speedups in quantum computing, but their generation and complete characterization present significant experimental and theoretical challenges that researchers are actively addressing.

Wigner functions reveal how dissipation strength alters the quantum states of squeezed vacuum (SV), even-parity, and odd-parity squeezed states over rescaled times of 0.1, 0.5, and 1.0.
Wigner functions reveal how dissipation strength alters the quantum states of squeezed vacuum (SV), even-parity, and odd-parity squeezed states over rescaled times of 0.1, 0.5, and 1.0.

Heralded Optical Amplification: A Deterministic Path to Non-Gaussianity

The Heralded Optical Parametric Amplifier (OPA) protocol enables the deterministic creation of non-Gaussian quantum states through a process of nonlinear optical interaction. Utilizing a nonlinear crystal within the OPA, a strong pump photon interacts with a vacuum state, generating signal and idler photon pairs. The protocol’s robustness stems from its ability to project the desired state by detecting one of these down-converted photons – the ‘herald’ – which collapses the overall state into a non-Gaussian form. This heralded measurement effectively filters the output, ensuring that only the desired non-Gaussian state is observed, offering a scalable pathway to complex quantum states beyond those attainable with Gaussian methods.

The Heralded OPA technique relies on inputting a squeezed vacuum state – a non-classical state with reduced noise in one quadrature – into an Optical Parametric Amplifier. The OPA, utilizing a nonlinear crystal, then generates correlated photon pairs via spontaneous parametric down-conversion. This process intrinsically creates entanglement between the signal and idler photons. The degree of entanglement and the specific properties of the resulting state are directly influenced by the pump characteristics and the properties of the input squeezed state. By manipulating these parameters, a variety of entangled states can be produced, forming the basis for heralded non-Gaussian state generation.

Detection of the ‘herald’ photon in the Heralded OPA protocol is the key to state preparation. This detection event signifies that a photon pair has been created in the nonlinear crystal, and collapses the output state into a superposition determined by the characteristics of the initial squeezed state and the OPA process. Specifically, this projection enables the generation of non-Gaussian states, including squeezed cat states, which exhibit quantum interference between coherent states. Current implementations using this technique have demonstrated high-fidelity states characterized by a coherent amplitude of approximately $α≈1.4$, indicating a substantial degree of non-classicality in the generated state.

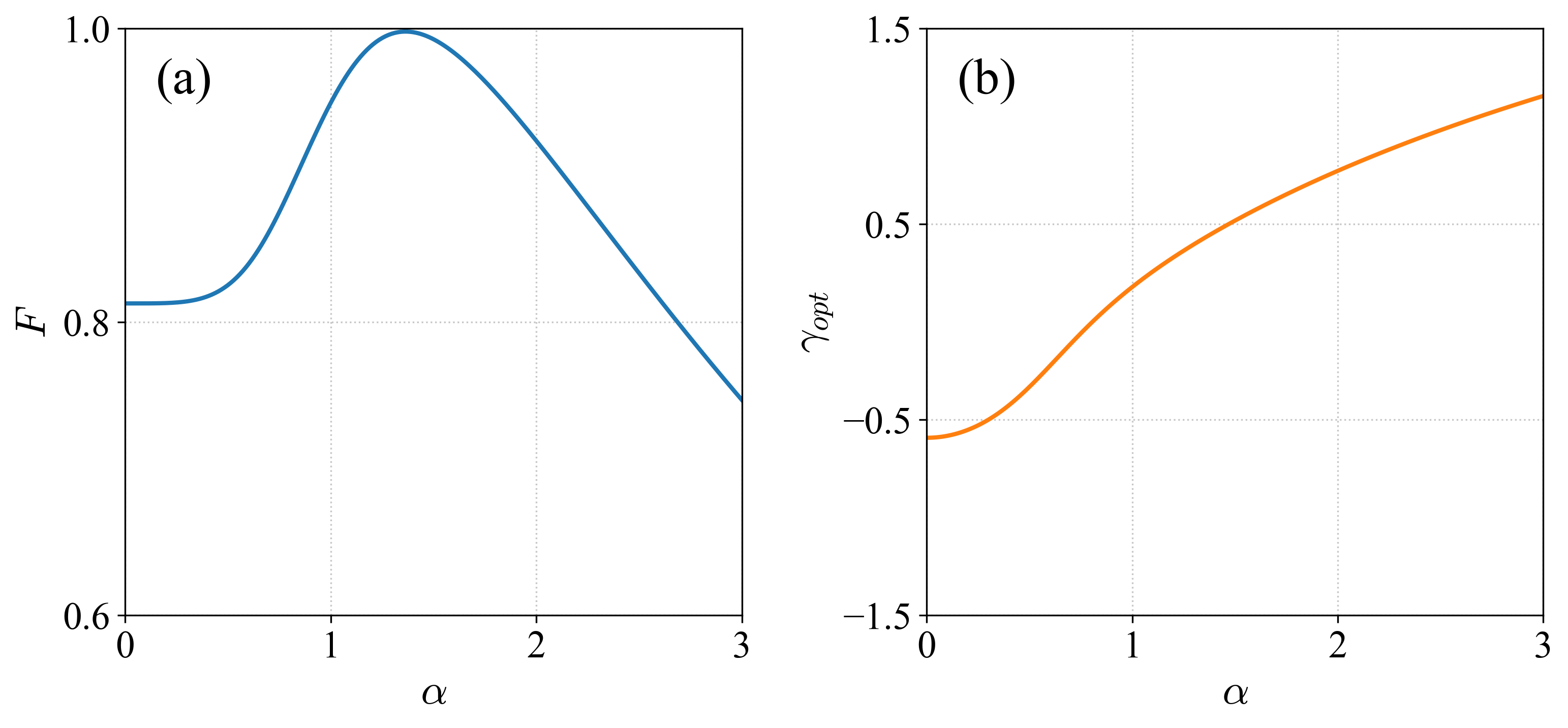
Optimal fidelity between the output state and a target squeezed state is achieved by tuning the squeezing parameter, as demonstrated by the corresponding parameter values that maximize fidelity.
Optimal fidelity between the output state and a target squeezed state is achieved by tuning the squeezing parameter, as demonstrated by the corresponding parameter values that maximize fidelity.

Characterizing Quantumness: The Significance of the Wigner Function

The Wigner function is a quasi-probability distribution used in quantum mechanics to represent a quantum state in phase space. Unlike classical probability distributions, the Wigner function can take on negative values, a key indicator of non-classical behavior. It provides a means to visualize quantum states, including those that are non-Gaussian – states which do not follow a Gaussian distribution and exhibit inherently quantum properties. By analyzing the Wigner function’s shape and identifying regions of negativity, researchers can characterize the quantumness of a state and differentiate it from any possible classical counterpart. The function is defined as the Fourier transform of the density operator’s diagonal elements in a particular basis, and is particularly useful for analyzing continuous variable systems, such as those involving harmonic oscillators and electromagnetic fields, allowing for a clear depiction of superposition and entanglement.

The Wigner function, a quasi-probability distribution in phase space, provides a means to identify non-classical states by evaluating its values; specifically, the presence of negative values within the Wigner function is a definitive indicator of non-classicality. Classical probability distributions are always non-negative, and therefore, any state exhibiting a negative Wigner function value demonstrably violates the constraints of classical mechanics. This negativity arises from the inherent quantum mechanical properties, such as superposition and entanglement, and serves as experimental verification that the generated quantum state cannot be described by any classical probability distribution, confirming the successful creation of a genuinely non-classical state, such as a squeezed state or a superposition of Fock states like $ |0\rangle – 1.4|2\rangle$.

Experimental results demonstrate the successful generation of high-fidelity photon number superpositions, specifically achieving fidelities greater than 0.99 for states including $|0\rangle – 1.4|2\rangle$. Furthermore, squeezed three-photon states were also generated with comparable fidelity. These results were obtained through precise control and manipulation of quantum states, validating the experimental setup’s capacity to produce non-classical light with minimal error. The observed fidelities represent a significant advancement in the creation of complex quantum states suitable for applications in quantum information processing and fundamental tests of quantum mechanics.

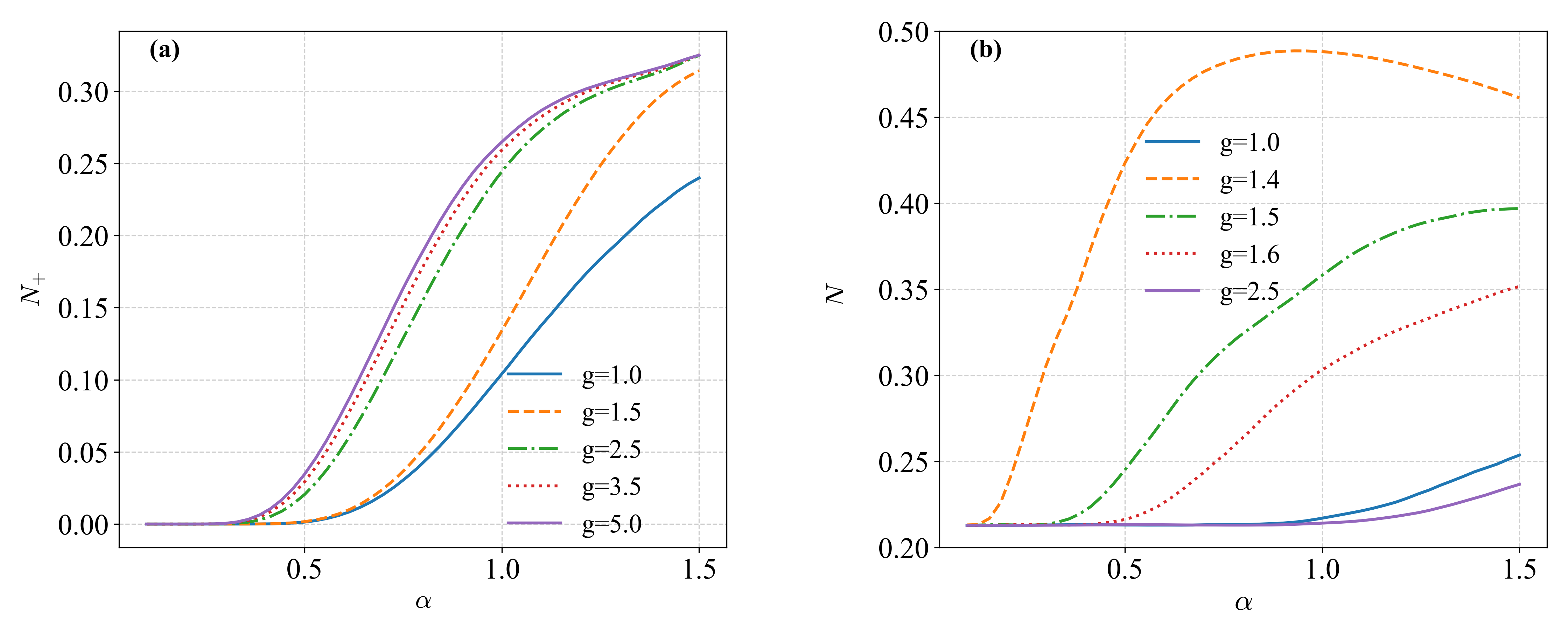
The volume of negative Wigner function decreases with increasing coherent state amplitude and is further modulated by the gain parameter.
The volume of negative Wigner function decreases with increasing coherent state amplitude and is further modulated by the gain parameter.

Towards Scalability: Mitigating Decoherence and Expanding Quantum Frontiers

Quantum states, the very foundation of quantum computation and communication, are remarkably fragile. A primary threat to their stability is photon loss, a ubiquitous decoherence mechanism that steadily erodes the non-classical properties essential for quantum information processing. As photons – the carriers of quantum information – are lost from a system, the superposition and entanglement that define quantum states begin to degrade, effectively introducing errors and limiting the duration over which quantum computations can be reliably performed. This loss isn’t merely a reduction in signal strength; it fundamentally alters the quantum state itself, driving it towards a classical mixture and diminishing the potential for exponential speedups promised by quantum technologies. Mitigating photon loss, therefore, is paramount to realizing practical and scalable quantum systems, demanding innovative approaches to both hardware design and error correction protocols.

A central challenge in quantum information science is maintaining the delicate quantum states necessary for computation and communication, a process threatened by decoherence. The Lindblad master equation offers a powerful and mathematically rigorous framework for understanding and predicting how these states evolve when interacting with their environment. This equation doesn’t simply describe the ideal, isolated quantum system, but explicitly accounts for the effects of dissipation and decoherence – such as photon loss – through the introduction of ‘jump operators’. These operators model the probabilistic transitions between quantum states caused by environmental interactions, effectively describing how a quantum system loses its coherence over time. By accurately modeling these decoherence mechanisms, the Lindblad master equation allows researchers to develop strategies for mitigating their effects and designing more robust quantum systems, paving the way for practical quantum technologies.

Recent advancements demonstrate the generation of quantum states at rates ranging from $10^5$ to $10^7$ states per second, achieved through the utilization of high-repetition-rate laser sources and exhibiting success probabilities between $10^{-4}$ and $10^{-2}$. These rates are competitive with established heralding schemes, signifying a considerable step forward in quantum information processing. Crucially, the integration of photonic circuits with highly sensitive superconducting detectors, coupled with the implementation of sophisticated protocols such as heralded optical parametric amplification (OPA), provides a promising architecture for constructing quantum systems that are not only robust against environmental noise but also inherently scalable, potentially enabling the realization of complex quantum computations and networks.

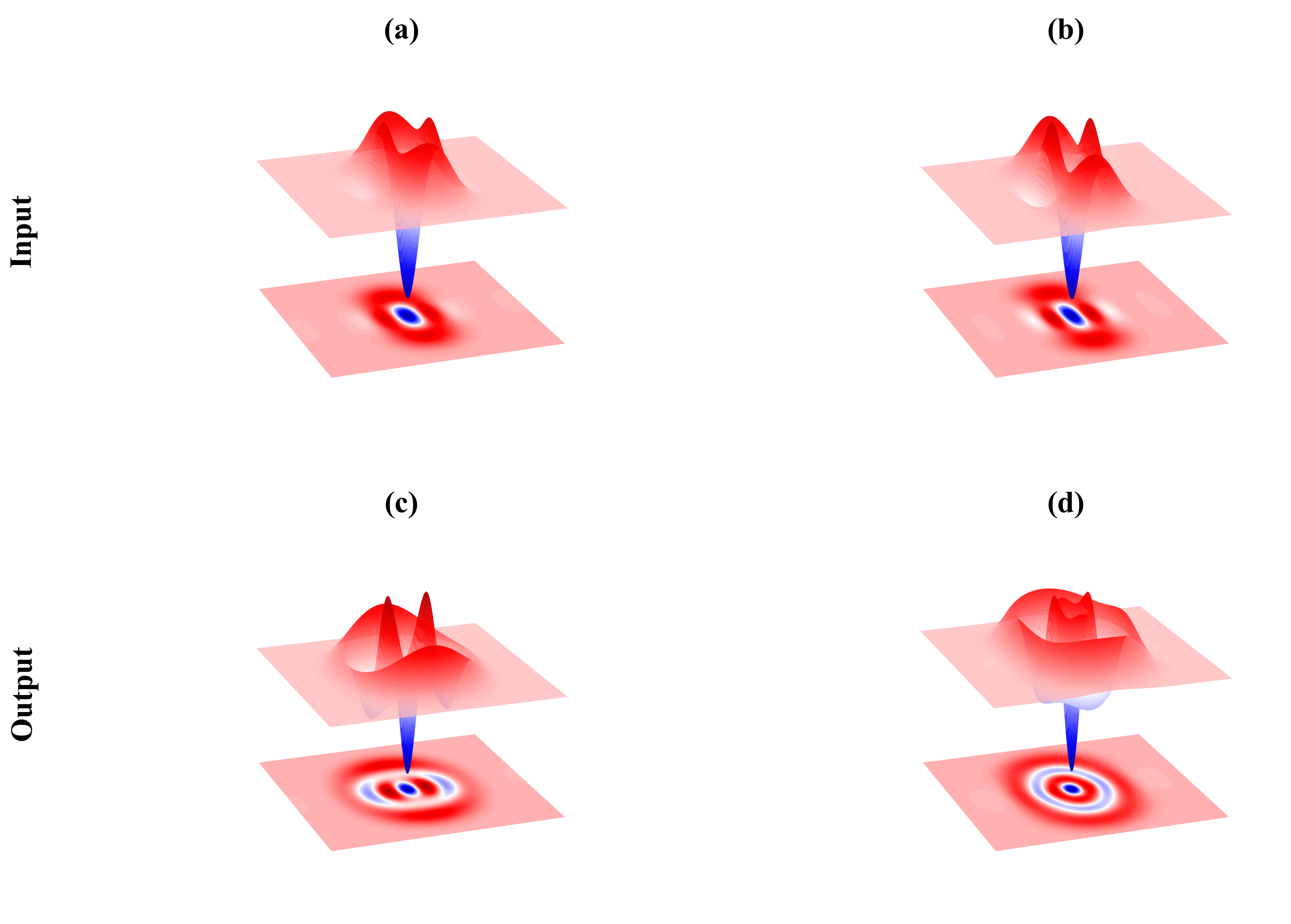
Wigner function analysis reveals that input odd SC states with varying coherent amplitudes (α=1.2 and α=1.5) are successfully amplified to corresponding signal states with gains of g=1.5 and g=g₀.
Wigner function analysis reveals that input odd SC states with varying coherent amplitudes (α=1.2 and α=1.5) are successfully amplified to corresponding signal states with gains of g=1.5 and g=g₀.

The pursuit of generating high-fidelity non-Gaussian states, as detailed in this work, demands a rigorous approach to quantum control. It is not sufficient for an algorithm to merely function; it must be demonstrably correct, mirroring mathematical elegance. This resonates with Paul Dirac’s assertion: “I have not the slightest idea what I am doing.” Though seemingly paradoxical, Dirac’s statement encapsulates the profound humility required when pushing the boundaries of theoretical physics and experimental quantum optics. The generalized heralded Optical Parametric Amplifier (OPA) protocol presented here embodies this spirit; each step, from squeezed state preparation to heralded measurement, must adhere to the immutable laws of quantum mechanics, leaving no room for approximation or empirical ‘fudge factors’.

Beyond the Horizon

The demonstrated generalized heralded Optical Parametric Amplifier (OPA) protocol, while a step toward deterministic generation of non-Gaussian states, does not, of course, resolve the fundamental issue of imperfection. Any real-world implementation will inevitably contend with photon loss-a nuisance that, rather than being merely mitigated, demands a mathematically rigorous characterization of the resulting state. A proof of robustness against such loss, detailing the acceptable bounds for maintaining fidelity, remains conspicuously absent. To claim ‘high fidelity’ without such a bound is, frankly, an exercise in optimistic empiricism.

Further investigation must address the scalability of this approach. The current protocol relies on heralded measurement, a process which, while elegant in principle, suffers from inherent probabilistic limitations. A deterministic, scalable architecture-one founded not on probability, but on provable state control-is the true objective. Simply increasing the complexity of the heralded system will not suffice; a fundamentally different approach is required. The Wigner function, as a diagnostic tool, has its limits; a more complete characterization of the generated states, potentially leveraging higher-order correlation functions, is necessary.

Ultimately, the value of this work lies not in the states generated today, but in the framework it provides for future inquiry. A successful theory of non-Gaussian state generation must be predicated on mathematical certainty, not experimental convenience. The pursuit of quantum information processing demands nothing less than a solution verifiable by proof, not merely by observation.

Original article: https://arxiv.org/pdf/2511.20946.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/

See also:

2025-11-28 09:10