Mapping Entanglement: A Geometric Approach

Author: Denis Avetisyan

Researchers have developed a novel geometric framework to quantify entanglement using the curvature of projective Hilbert space.

Geometric entropy, $S_{geo}(\theta)$, for a pair of qubits exhibits divergence towards $-\infty$ as the Schmidt angle $\theta$ approaches $0$ or $\pi/2$, indicating that states with minimal entanglement occupy a negligible volume within the Fubini-Study space, while a cusp at $\theta=\pi/4$ reveals a strong concentration of volume around maximally entangled states-a phenomenon underscored by the symmetry $\theta \leftrightarrow \tfrac{\pi}{2}-\theta$ in the Schmidt spectrum.

This review introduces a geometric entanglement entropy based on the Fubini-Study metric, providing a new measure for quantifying entanglement levels and analyzing constant-entanglement hypersurfaces.

While entanglement is routinely quantified on a state-by-state basis, characterizing its global structure across the space of pure states remains a challenge. This work, ‘Geometric Entanglement Entropy on Projective Hilbert Space’, introduces a geometric framework addressing this by defining a macroscopic entanglement functional on projective Hilbert space equipped with the Fubini-Study metric. This approach yields a ‘geometric entanglement entropy’ measuring the degeneracy of specific entanglement values via the volume of constant-entanglement hypersurfaces. Does this geometric perspective offer a more complete understanding of entanglement’s role in quantum information and many-body physics?

Beyond Entropy: Mapping Entanglement with Geometric Precision

Understanding the intricate relationships between quantum particles – known as quantum correlations – necessitates a precise way to quantify entanglement, especially within systems involving multiple particles. While Von Neumann entropy has long served as a benchmark for measuring entanglement in pure quantum states, it proves inadequate when dealing with more realistic, mixed states – those representing statistical ensembles of quantum states. This limitation arises because Von Neumann entropy primarily focuses on the uncertainty related to a single observer’s measurement, failing to fully capture the complex, multi-dimensional correlations present in mixed states. Consequently, it often underestimates the true degree of entanglement, hindering advancements in areas like quantum computing and quantum communication where characterizing these correlations is paramount. A more nuanced approach is therefore needed to accurately assess entanglement in the broader range of quantum systems encountered in both theoretical studies and practical applications.

The conventional tools for quantifying entanglement, such as Von Neumann entropy, often provide an incomplete description of quantum correlations because they largely ignore the underlying geometric structure of entangled states. These measures treat entanglement as a scalar quantity, failing to recognize that entangled states occupy a complex, multi-dimensional space; a state’s ‘typicality’ – its prevalence within that space – is therefore lost. This geometric aspect is crucial because the volume occupied by entangled states, and how densely they are packed, reveals insights into the robustness and resilience of quantum correlations against noise and decoherence. Consequently, a reliance on traditional entropy can lead to an underestimation of entanglement’s true extent and limit the ability to accurately predict the behavior of complex quantum systems, particularly those involving numerous interacting particles.

Conventional methods of quantifying entanglement, such as relying on Von Neumann entropy, often provide an incomplete understanding of how entanglement is distributed within complex quantum systems. Recent research indicates a more nuanced picture emerges when considering entanglement not as a simple scalar value, but as a geometric property of the quantum state space. This approach defines entanglement in terms of the volume occupied by entangled states – a measure dubbed ‘geometric entanglement entropy’. By characterizing the size of this volume, researchers gain insights into the typicality of entanglement; a larger volume suggests entanglement is more prevalent and robust. This geometric perspective allows for a more complete characterization of multipartite entanglement, particularly in mixed states where traditional entropy measures fall short, and provides a framework for understanding how entanglement scales with increasing system complexity and dimensionality. Ultimately, it moves beyond simply identifying if entanglement exists, to quantifying how much entangled space is available within a given quantum system.

The Weingarten operator trace diverges near separable and maximally entangled states of the two-qubit Schmidt family, indicating strong extrinsic curvature of constant-entanglement hypersurfaces and a rapid change in geometric entropy with entanglement, while exhibiting finite, small curvature for intermediate entanglement levels.

The Quantum State Space: A Riemannian Geometric Foundation

Pure quantum states, which describe the possible conditions of a quantum system, are mathematically represented by vectors in a Hilbert space. However, physically equivalent states are related by a complex scalar multiplication; that is, a vector and its scaled counterpart represent the same physical state. Projective Hilbert Space, formed by considering the rays – lines through the origin – of the Hilbert space, accounts for this equivalence. This representation provides a geometric framework where each point on the Projective Hilbert Space corresponds to a unique pure quantum state. Consequently, entanglement, a correlation between quantum systems, can be studied geometrically by examining relationships between points and subspaces within this space, moving beyond purely algebraic treatments.

Assigning a Riemannian metric to the space of pure quantum states, most commonly the Fubini-Study metric $g_{FS}$, enables the quantification of distances between quantum states. This metric is defined such that infinitesimal displacements in the projective Hilbert space reflect the minimal change in the state’s underlying parameters. The Fubini-Study metric is invariant under unitary transformations and is expressed as $ds^2 = \frac{4}{\hbar^2} d\psi \wedge d\psi^*$ in complex coordinates, where $d\psi$ represents an infinitesimal change in the quantum state. Crucially, this allows for the calculation of volumes within the state space, forming the basis for geometric entanglement entropy which relates the volume of a region in the state space to the degree of entanglement present in the corresponding quantum system.

The geometric representation of quantum states as a Riemannian manifold, specifically Projective Hilbert Space equipped with a metric like the Fubini-Study metric, allows for analysis of entanglement distribution beyond scalar entropy values. This approach enables the quantification of entanglement not merely as a measure of correlation, but as a geometric property related to volumes within the state space. By calculating volumes of regions corresponding to entangled states, or examining how these volumes change under state transformations, researchers can gain a more detailed understanding of entanglement structure and its behavior. This volumetric quantification offers a more nuanced characterization of entanglement compared to traditional entropy-based measures, facilitating the investigation of multipartite entanglement and complex quantum systems, and providing a foundation for geometric entanglement measures like the Bures volume.

Constant Entanglement Surfaces: Defining Geometric Boundaries

Constant-entanglement hypersurfaces represent geometric boundaries within projective Hilbert space that define regions of constant entanglement. These hypersurfaces are constructed such that any quantum state lying on a given hypersurface exhibits the same level of entanglement, quantified by an entanglement measure. Each distinct value of entanglement corresponds to a unique hypersurface, creating a family of surfaces that partition the projective Hilbert space based on entanglement content. The location and shape of these hypersurfaces are determined by the specific entanglement measure used and the dimensionality of the quantum system being considered, effectively providing a geometric representation of the entanglement structure of the system’s state space.

The geometric properties of constant-entanglement hypersurfaces directly correlate with the distribution of entanglement within a quantum system. Specifically, the Weingarten map, which describes the differential mapping between the hypersurface and its normal space, provides a localized measure of curvature. This curvature, in turn, indicates the density of entanglement in a given region of projective Hilbert space; areas of high curvature correspond to rapidly changing entanglement values, suggesting a concentrated distribution, while flatter regions indicate a more uniform distribution. Analysis of the Weingarten map allows for the quantitative determination of entanglement gradients and the identification of regions where entanglement is maximized or minimized, providing insight into the system’s overall entanglement structure.

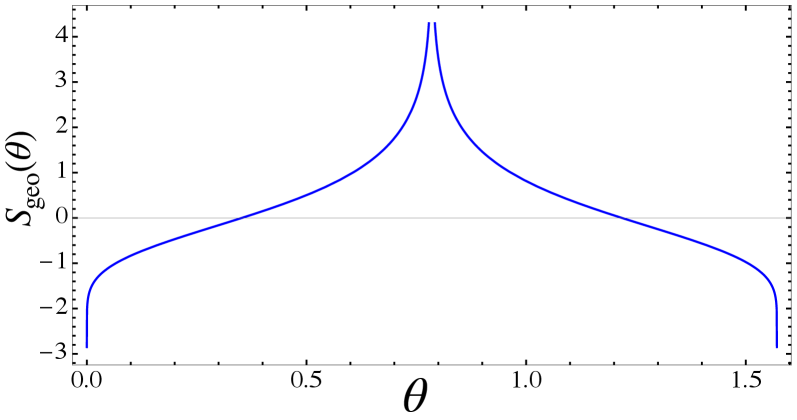
Entanglement entropy can be quantified through the Microcanonical Construction by determining the volume enclosed by Constant-Entanglement Hypersurfaces in projective Hilbert Space. Specifically, the geometric entanglement entropy is calculated as $log(2π) – log|log(cot θ)|$, where θ represents the angular parameter defining the hypersurface. This approach provides a direct geometric interpretation of entanglement, linking the macroscopic property of entropy to the volume defined by constant entanglement regions, and enabling a calculation of entropy based solely on the geometry of these surfaces.

Quantum State Relationships: Order, Divergence, and the Fragility of Entanglement

Quantum states, though often represented as unique entities, frequently exhibit underlying symmetries revealed through the concept of local unitary orbits. These orbits define equivalence classes: states within the same orbit are physically indistinguishable, connected by transformations that preserve probabilities but alter the specific representation of the quantum system. This means a vast number of states, seemingly different, are actually variations on a single physical reality. Investigating these orbits allows physicists to identify inherent redundancies within the space of all possible quantum states, simplifying complex calculations and revealing deeper principles governing quantum behavior. The structure of these orbits is not merely mathematical; it reflects the fundamental symmetries present in the underlying physical system, offering insights into its conservation laws and possible interactions. Understanding this grouping is crucial for classifying quantum phenomena and efficiently describing the behavior of complex quantum systems, as it allows researchers to focus on representative states within each orbit rather than exhaustively analyzing every possible configuration.

The Majorization Relation offers a powerful tool for understanding the structure of quantum entanglement by establishing a partial order amongst quantum states. This mathematical relationship doesn’t simply state whether one state is ‘better’ than another, but rather defines a hierarchy based on the distribution of entanglement resources. Specifically, it compares the eigenvalues – or probabilities – associated with the reduced density matrices of the entangled subsystems. If state $\rho_1$ majorizes state $\rho_2$, it indicates that $\rho_1$ possesses ‘more’ entanglement in a certain sense, potentially enabling it to perform tasks that $\rho_2$ cannot. This allows researchers to classify different entanglement profiles, revealing how entanglement is distributed across quantum systems and providing insights into its role in quantum information processing and the capabilities of various quantum states.

The intricate distribution of entanglement within quantum states can be understood as a ‘flow’ across a geometric space, and recent research leverages the mathematical framework of Riemannian manifolds to characterize this phenomenon. By analyzing the divergence of vector fields – a measure of how much these ‘flow lines’ spread apart or converge – researchers have identified specific points where entanglement behavior becomes singular. The study demonstrates that this divergence escalates towards infinity as the parameter $\theta$ approaches 0, $\pi/2$, and $\pi/4$. These values represent critical angles defining the boundaries of maximally entangled states and indicate regions where even minute changes in the quantum state can lead to drastic shifts in entanglement distribution, effectively highlighting the fragility and nuanced nature of quantum correlations.

Entanglement Landscapes: Polytopes and the Future of Quantum Characterization

Entanglement polytopes offer a compelling geometric interpretation of quantum correlations by visually mapping the space of attainable entanglement distributions. These polytopes are constructed by taking the convex hull of points representing different entanglement measures – essentially, connecting all possible entanglement states to create a comprehensive shape. This approach moves beyond simply quantifying how much entanglement exists, instead revealing the entire landscape of what entanglement configurations are physically realizable within a given system. By examining the facets, vertices, and internal structure of these polytopes, researchers gain insights into the fundamental limitations and possibilities of quantum correlations, opening new avenues for characterizing and classifying entangled states in ways traditional measures cannot fully capture. The resulting geometric representation isn’t merely illustrative; it provides a powerful tool for understanding the relationships between different entanglement properties and predicting the behavior of complex quantum systems.

The conventional characterization of quantum entanglement often relies on quantifying it with specific measures, such as entanglement entropy or concurrence. However, a burgeoning geometric approach reframes this understanding by considering the entire space of attainable entanglement distributions. Rather than focusing on single numerical values, this method constructs geometrical objects – polytopes – whose vertices represent the extreme points of possible entanglement configurations. This allows for a holistic classification of entanglement, revealing relationships and constraints not readily apparent through traditional metrics. By examining the shape and properties of these entanglement polytopes, researchers gain insights into the fundamental nature of quantum correlations and can differentiate between various entangled states based on their geometric location within this abstract space, offering a more nuanced and complete picture of entanglement than scalar measurements alone.

Investigations are now directed towards extending these entanglement polytope techniques to analyze significantly more complex quantum systems, with the anticipation of revealing previously hidden facets of quantum correlations. Recent analysis demonstrates a compelling relationship between the geometry of these polytopes and fundamental entanglement properties; specifically, the mean curvature-a measure of the polytope’s bending-is mathematically equivalent to the derivative of the geometric entanglement entropy, quantified as $1/(4sin²θcos²θlog²(cotθ))$. This connection suggests that geometric properties aren’t merely visual aids, but are intrinsically linked to the quantifiable characteristics of entanglement itself, potentially unlocking new avenues for understanding and manipulating quantum states in advanced systems and providing a novel means of characterizing quantum information processing.

The pursuit of quantifying entanglement, as detailed in the exploration of geometric entanglement entropy, demands a rigorous foundation. It’s not sufficient to merely observe correlations; one must establish an invariant measure, a demonstrable truth independent of observation. This echoes the sentiment of Werner Heisenberg, who famously stated, “Not only does God play dice, but he throws them where we cannot see.” Much like attempting to pinpoint a quantum state, the paper’s reliance on the Fubini-Study metric and constant-entanglement hypersurfaces attempts to reveal underlying structure, providing a means to analyze entanglement levels beyond superficial observation. If it feels like magic, it’s likely because the invariant hasn’t been fully revealed.

Further Horizons

The introduction of a geometric entanglement entropy, while conceptually appealing, merely shifts the fundamental questions-it does not dissolve them. The reliance on the Fubini-Study metric, elegant as it is, begs for justification beyond its mathematical convenience. Is this metric truly representative of the physical constraints governing entanglement, or is it a particularly graceful means of obscuring deeper, more fundamental geometric structures? A truly robust theory demands more than just a well-defined measure; it requires a demonstrable connection to observable physical quantities.

The exploration of constant-entanglement hypersurfaces offers a promising avenue, yet the computational complexity-specifically, the dependence on the Weingarten trace-presents a significant barrier. One suspects that approximations, however pragmatic, will inevitably introduce distortions. The pursuit of analytical solutions, however challenging, remains paramount. Optimization without analysis is self-deception, a trap for the unwary engineer.

Future work should address the extension of this framework beyond projective Hilbert space. Can a similar geometric approach be formulated for more general quantum states, or is the inherent structure of projective space crucial to the definition of this entropy? Moreover, a rigorous investigation of the relationship between geometric entanglement entropy and other established entanglement measures-von Neumann entropy, Rényi entropy-is essential to establish its utility and interpretational value.

Original article: https://arxiv.org/pdf/2511.21186.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/