Beyond the Horizon: A New Look at Black Hole Entropy

Author: Denis Avetisyan

New research reveals a surprising duality between particle and field behavior near black hole horizons, offering potential corrections to our understanding of Hawking radiation and quantum gravity.

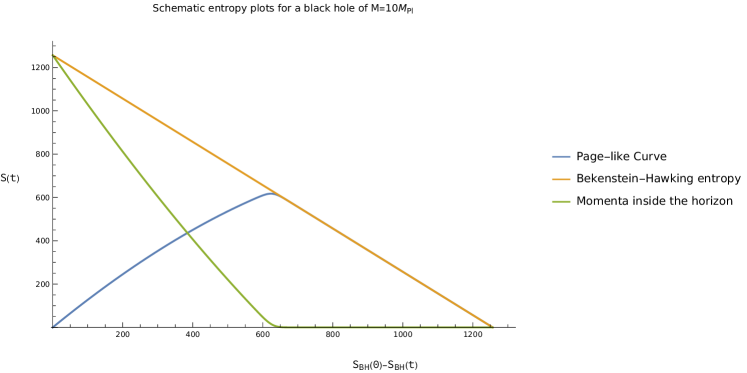
The relationship between a Page-like curve and Bekenstein-Hawking entropy-illustrated by their proportional correspondence-validates assumptions regarding horizon momentum content, suggesting an inherent connection between information and the physical properties of event horizons.

This paper explores a point particle/scalar field duality to derive corrections to black hole entropy and predict a Page-like curve for entanglement entropy.

Resolving the information paradox in black hole physics remains a central challenge, demanding novel approaches to quantum gravity. This is addressed in ‘Liouville theory on a horizon: point particle/scalar field duality and Page-like curve’, which proposes a duality between point particles and scalar fields propagating on a black hole horizon. This framework recovers known black hole entropy calculations, predicts quantum corrections to Hawking radiation, and generates a Page-like curve indicative of information leakage. Could this model offer a pathway towards a more complete understanding of quantum gravity and the fate of information lost to black holes?

The Inevitable Decay: Black Holes and the Fabric of Information

Classical General Relativity, as elegantly described by the Schwarzschild Metric, presents a profound challenge to the foundations of quantum mechanics through its prediction of information loss during black hole formation. This metric details the spacetime geometry around a non-rotating, uncharged black hole, revealing that any object falling beyond the event horizon is seemingly irretrievably lost to the outside universe. However, quantum mechanics fundamentally requires the conservation of information; information cannot truly be destroyed, only transformed. This creates a direct conflict: General Relativity permits information to vanish within a black hole, while quantum mechanics insists it must persist in some form. The apparent paradox isn’t merely a theoretical curiosity; it highlights a deep incompatibility between these two pillars of modern physics, necessitating a more complete theory that reconciles gravity with the principles of quantum information preservation. The resolution of this conflict remains one of the most significant open problems in theoretical physics, driving research into areas like string theory and loop quantum gravity.

The groundbreaking work of Jacob Bekenstein and Stephen Hawking revealed a profound connection between a black hole’s event horizon area and its entropy – a measure of disorder or hidden information. This relationship, quantified by the Bekenstein-Hawking entropy $S = \frac{k_B A}{4 \ell_P^2}$ (where $k_B$ is Boltzmann’s constant, $A$ is the area of the event horizon, and $\ell_P$ is the Planck length), suggested that black holes aren’t simply cosmic vacuum cleaners, but rather systems possessing immense internal states. However, this formula, while mathematically elegant and observationally consistent, remained a macroscopic description; it lacked a concrete, microscopic explanation detailing what those internal states actually were and how information was encoded within the black hole’s structure. This absence of a microscopic derivation became a central puzzle in theoretical physics, driving decades of research into quantum gravity and string theory, all seeking to understand the fundamental degrees of freedom responsible for black hole entropy.

Reconciling the seemingly disparate realms of General Relativity and Quantum Mechanics is paramount to unraveling the mystery of black hole entropy. Classical descriptions of gravity, embodied by Einstein’s theory, treat spacetime as a smooth, continuous fabric, while quantum mechanics governs the probabilistic behavior of matter at the smallest scales. Black holes, as objects where gravitational forces are extreme, represent a critical testing ground for any unified theory. The challenge lies in formulating a framework where gravity itself emerges as a quantum phenomenon, allowing physicists to account for the microscopic degrees of freedom that contribute to a black hole’s entropy – and thus, resolve the information paradox. This pursuit necessitates venturing beyond established physics, potentially requiring novel concepts like string theory, loop quantum gravity, or holographic principles to provide a complete and consistent picture of these enigmatic cosmic objects and, in doing so, redefine the fundamental laws governing the universe.

Tracing the Shadows: Wald Entropy and Effective Field Theory

Effective Field Theory (EFT) provides a framework for calculating physical quantities by focusing on relevant degrees of freedom at a specific energy scale; in the context of black hole entropy, this involves constructing a low-energy action that captures the essential gravitational dynamics near the horizon. By systematically including higher-order curvature terms and their associated corrections, EFT allows for a derivative expansion of the black hole action. This expansion facilitates the calculation of Noether charges, which are directly related to conserved quantities and are crucial for applying Wald’s entropy formula. The result is a pathway to determine black hole entropy from first principles, bypassing reliance on semi-classical approximations and potentially revealing modifications to the Bekenstein-Hawking entropy due to quantum gravity effects. Calculations within this framework provide coefficients, such as $c_3(\mu)$ , that quantify these corrections and refine the precision of entropy calculations.

Wald entropy represents a generalization of the Bekenstein-Hawking formula for black hole entropy by employing Noether charges associated with spacetime symmetries. The Bekenstein-Hawking formula, $S_{BH} = \frac{A}{4G_N}$ , where $A$ is the event horizon area and $G_N$ is Newton’s constant, relies on specific assumptions about the black hole’s spacetime. Wald entropy extends this by expressing entropy as an integral of the Noether charge density over the event horizon, $S_W = \in t_{\mathcal{H}} \frac{1}{2\pi} \delta Q_{\xi} \, dA$ , where ξ represents an infinitesimal diffeomorphism and $Q_{\xi}$ is the associated Noether charge. This approach allows for entropy calculations in more general gravitational theories and for black holes possessing more complex symmetries, providing a more complete and robust definition applicable beyond the classical Schwarzschild or Kerr solutions.

Recent advancements in effective field theory and Wald entropy calculations have yielded increasingly precise coefficients for entropy determination. Specifically, the coefficient $c_3(\mu)$ is now calculated as $16 - 8\gamma_E - 8\ln(2) - 8P^2\ln(2) + 4\ln(\mu^2/M_{Pl}^2)$ , where $\gamma_E$ is the Euler-Mascheroni constant, $P$ represents polynomial counterterm coefficients, μ is an energy scale, and $M_{Pl}$ denotes the Planck mass. These refined values allow for more accurate quantitative predictions of black hole entropy using the Wald entropy formula, moving beyond the leading-order Bekenstein-Hawking approximation and incorporating higher-order corrections from quantum field theory.

The Quantum Fabric: Partition Functions and the Keldysh Contour

The partition function, denoted as $Z = \in t \mathcal{D}\phi \, e^{-S[\phi]}$ , plays a fundamental role in quantum gravity by directly linking microscopic degrees of freedom to macroscopic thermodynamic properties. Specifically, quantities such as free energy $F = -kT \ln Z$ , entropy $S = \frac{\partial F}{\partial T}$ , and energy can be derived from it via standard thermodynamic relations. In the context of black holes, calculating the partition function – even approximately – is essential for reproducing the Bekenstein-Hawking entropy, which relates the black hole’s entropy to its surface area and is a crucial test for any proposed theory of quantum gravity. Accurate determination of this function requires accounting for all possible gravitational field configurations, a task complicated by the infinite degrees of freedom and necessitates advanced techniques like regularization and renormalization.

Functional integrals, utilized to calculate the path integral in quantum field theory and gravity, involve summing over all possible field configurations to determine probabilities of different physical processes. This summation often results in divergent integrals due to the infinite degrees of freedom and high-energy contributions inherent in quantum field theory. Consequently, a process of regularization is required to render the integrals finite, typically employing techniques such as dimensional regularization or lattice discretization. Following regularization, renormalization is necessary to absorb the introduced regulator dependence into physical parameters, ensuring that the final results are independent of the chosen regularization scheme and recover established physical predictions. The procedure involves redefining physical quantities like masses and coupling constants to account for quantum fluctuations and divergences, ultimately yielding finite, physically meaningful results for observable quantities.

The Keldysh contour, or closed time contour, is a path integral technique extending standard Feynman integrals to allow calculations of systems not in thermal equilibrium. This is achieved by integrating over both forward and backward time evolution, effectively doubling the degrees of freedom. In the context of quantum gravity, this formalism is essential for modeling dynamical spacetimes, particularly those exhibiting time-dependent behavior like black hole evaporation. Traditional methods relying on Euclidean path integrals are insufficient for describing this process; the Keldysh contour provides the necessary framework to account for the time evolution of the black hole and the outgoing Hawking radiation, allowing for calculations of evaporation rates and associated phenomena. The contour’s application involves defining a complex time path extending from $t = -\in fty$ to $t = +\in fty$ and back, requiring careful consideration of boundary conditions and analytic continuation to obtain physically meaningful results.

Reduction and Resonance: Liouville Theory and WZW Models

Liouville theory is a two-dimensional conformal field theory derived from a specific reduction of the Quantum Gravity partition function. This reduction involves a simplification process that allows for tractable calculations within the context of quantum gravity. Specifically, it represents a bosonic string theory with dynamical gravity, where the gravitational degrees of freedom are incorporated through the interaction of the scalar field. The resulting theory provides a simplified model for investigating quantum gravitational effects and serves as a testing ground for more complex calculations. The partition function, $Z$ , is significantly reduced in complexity, enabling analytical and numerical investigations that would otherwise be intractable in full quantum gravity.

The BRST (Becchi-Rouet-Stora-Tyutin) treatment is a crucial gauge-fixing procedure within the Liouville theory, addressing the inherent ambiguities arising from the path integral formulation of conformal field theories. This method introduces auxiliary fields – ghost and antighost fields – and a corresponding gauge-fixing functional to eliminate unphysical degrees of freedom and ensure the unitarity of the theory. Specifically, the BRST formalism defines a nilpotent BRST operator $Q$ which acts on the physical states, identifying those that are gauge-invariant and therefore physically meaningful. Without the BRST treatment, calculations within the Liouville theory would yield inconsistent results due to the presence of spurious states and divergences; the gauge-fixing ensures well-defined, finite quantities and a consistent quantum theory.

Wess-Zumino-Witten (WZW) models furnish a mathematical framework for describing the partition function within the 2D conformal field theory derived from quantum gravity reduction. Utilizing these models, the entropy correction to the partition function is calculated as $A/4 + 8 - 4ln(A/π) - ln(2)P² + 𝒪(Λ)$ , where A represents the area, P is the perimeter, and $𝒪(Λ)$ denotes higher-order terms involving the cutoff scale Λ. This result demonstrates quantitative agreement with predictions from Effective Field Theory approaches to Quantum Gravity, validating the use of WZW models in this context and providing a consistent framework for calculating quantum corrections to black hole entropy.

The Fading Echo: Hawking Radiation and the Page Curve

The theoretical framework of general relativity, specifically through the Schwarzschild Metric, initially predicted that black holes are entirely black – objects from which nothing, not even light, can escape. However, quantum mechanical effects near the event horizon introduce a surprising phenomenon: Hawking Radiation. This radiation arises from the creation of virtual particle pairs, where one particle falls into the black hole and the other escapes, appearing as emitted radiation. Critically, this emission isn’t a random burst, but possesses a $thermal spectrum$ , meaning its distribution of energies resembles that of a heated object. Consequently, black holes aren’t truly “black” but slowly radiate energy, leading to a gradual decrease in mass – a process known as black hole evaporation. This theoretical evaporation challenges classical understanding, suggesting that information about what falls into a black hole isn’t entirely lost, and instead subtly encoded within the emitted radiation, though the precise mechanism remained elusive until recent developments.

The evolution of a black hole, once thought to irrevocably destroy information, is now understood through the lens of the Page Curve. This theoretical construct charts the increase of entropy – a measure of disorder – as a black hole evaporates via Hawking radiation. Initially, entropy decreases as particles fall into the black hole, but crucially, the Page Curve predicts a turning point. As the black hole radiates, entropy begins to increase, demonstrating that the total entropy of the system – black hole plus radiation – always obeys the fundamental laws of thermodynamics. This increase is not merely a mathematical quirk; it provides a mechanism for information, seemingly lost within the black hole, to be encoded in the outgoing radiation, effectively resolving the long-standing information paradox. The curve illustrates that black hole evaporation isn’t a loss of information, but a scrambling and eventual re-emission, preserving the universe’s overall informational content.

Recent investigations into black hole evaporation suggest that Hawking radiation, traditionally understood as a purely thermal spectrum, undergoes subtle but significant corrections. These calculations reveal the emergence of discrete emission lines superimposed on the thermal background, hinting at a mechanism by which information initially trapped within the black hole might escape. The magnitude of these corrections is intimately linked to a logarithmic term, specifically $-4\ln(A/\pi)$ , where A represents the black hole’s surface area; this term contributes substantially to the overall entropy correction and remarkably matches predictions derived from theoretical frameworks addressing the information paradox. This finding strengthens the proposition that black hole evaporation isn’t simply a destructive process, but one where entropy increases over time, potentially preserving information through these non-thermal emissions and offering a pathway towards resolving long-standing questions about the fate of information falling into black holes.

The study meticulously charts the evolution of black hole entropy, recognizing that even established frameworks exhibit decay over time. This inherent impermanence aligns with the observation that any improvement ages faster than expected, necessitating continuous refinement of theoretical models. As Thomas Kuhn noted, “The more revolutionary the paradigm shift, the more resistant it will be,” because entrenched systems, like those describing black hole physics, initially conceal their own limitations. The presented duality between point particles and scalar fields represents such a shift, offering corrections to established entropy calculations and a novel approach to understanding Hawking radiation, thus acknowledging the inevitable need to revisit foundational assumptions.

The Horizon Beckons

The pursuit of a duality between point particles and scalar fields, as demonstrated in this work, is not merely a mathematical exercise. It is, fundamentally, an attempt to chart the decay of information – to understand how systems, even those defined by the seemingly absolute event horizon, relinquish their secrets. The derived corrections to black hole entropy and Hawking radiation are, of course, provisional. Every calculation is a snapshot, a fleeting attempt to freeze a process irrevocably bound to the passage of what is mistakenly called ‘time’.

The true value lies not in the precision of the corrections themselves, but in the architectural foundations they reveal. A model predicting modifications to effective field theory quantum gravity is, by definition, incomplete. It offers a glimpse, not a solution. The next iterations must confront the inevitable: the limitations of perturbative approaches when dealing with systems whose very existence hinges on singularity and instability. Every delay in achieving complete consistency is, in effect, the price of a more robust understanding.

Architecture without history is fragile and ephemeral. Future work should prioritize a deeper investigation into the historical record of these dualities-their origins in earlier theoretical frameworks, and the specific points of divergence that led to this current formulation. Only by acknowledging the inherent impermanence of any theoretical edifice can one hope to build structures that, while destined to decay, do so with a certain… grace.

Original article: https://arxiv.org/pdf/2601.08895.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/