Author: Denis Avetisyan
A novel theoretical framework proposes our universe arose from the symmetry breaking within a multiverse, potentially solving long-standing cosmological mysteries.
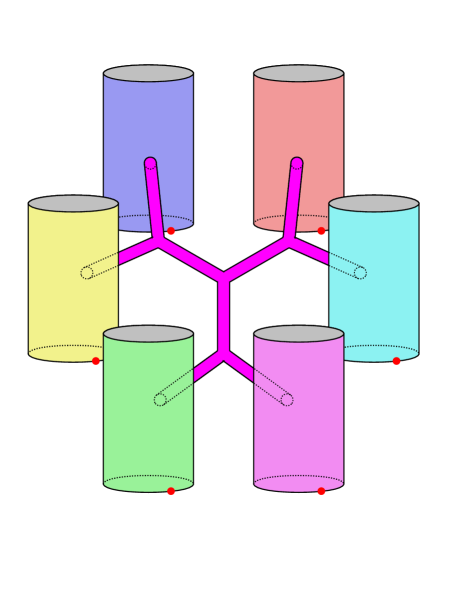
![Distinct one-dimensional universes, differentiated by inherent characteristics, are unified through the exchange of traversable wormholes, resulting in a propagating two-dimensional construct evolving with time-a process facilitated by designated reference points within each original universe, as detailed in prior work [8, 3].](https://arxiv.org/html/2601.10499v1/x1.png)
This review explores a model linking W3 algebras, Jordan algebras, and a ‘knitting’ mechanism involving wormholes to address the cosmological constant problem and the emergence of the Friedmann universe.
Current cosmological models struggle to reconcile observed phenomena like the smallness of the cosmological constant with fundamental physical principles. In the article ‘The emergence of our Universe’, we explore a novel framework wherein our universe arises from the symmetry breaking of a multicomponent $W_3$ algebra, intricately linked to Jordan algebras and a ‘knitting’ mechanism involving potential wormhole connections. This process generates an extended spacetime governed by a modified Friedmann equation, offering a potential resolution to several outstanding cosmological puzzles. Could this multiverse model, rooted in algebraic symmetry, provide a more complete understanding of our universe’s origin and evolution?
The Unfolding of Spacetime: From Algebra to Multiverse
Contemporary cosmological models face a significant challenge in harmonizing the principles of quantum mechanics with the observed accelerating expansion of the universe. Attempts to describe gravity at the quantum level, crucial for understanding the universe’s earliest moments and the nature of black holes, often lead to mathematical inconsistencies and predictions that clash with observational evidence. Specifically, general relativity, the current best description of gravity, breaks down at extremely small scales where quantum effects dominate. This incompatibility necessitates the exploration of new theoretical frameworks, such as string theory or loop quantum gravity, yet these approaches also encounter hurdles in explaining the universe’s large-scale structure and the measured value of dark energy driving its accelerated expansion. The persistent tension between quantum gravity and cosmological observations highlights a fundamental gap in ΛCDM model and motivates investigations into alternative descriptions of spacetime itself.
A new Multiverse Model proposes that spacetime isn’t a pre-existing framework, but rather an emergent property arising from the breaking of symmetry within a W_3W_{\in fty} algebra. This algebraic structure, far more fundamental than the universe as currently understood, dictates the possible configurations of reality. The model posits that the familiar dimensions of space and time aren’t absolute, but are instead a consequence of this symmetry breaking – a process where a highly symmetrical, initial state transitions into the less symmetrical universe observed by cosmological instruments. Essentially, the very fabric of reality, including its geometry and topology, is not a given, but a derived phenomenon – a complex outcome of underlying algebraic rules, suggesting a deeper, more interconnected multiverse beyond our immediate perception.
The conventional understanding of the universe as a foundational entity may be incomplete; this model posits that our reality isn’t the bedrock of existence, but rather an emergent phenomenon. It proposes a deeper, more fundamental level of reality governed not by spacetime itself, but by the abstract rules of a W_{3} algebra – a mathematical structure defining symmetries and relationships. Just as temperature emerges from the collective motion of molecules, spacetime, and all its contents, arises from the symmetry breaking within this algebraic framework. This challenges the notion of a pre-existing universe, suggesting instead that the laws of physics as experienced within our cosmos are effective descriptions, valid only within the specific conditions created by this emergent process. The implications extend beyond cosmology, hinting at a potentially infinite landscape of universes, each governed by unique algebraic configurations and therefore potentially exhibiting drastically different physical laws.
The Multiverse Model posits that the familiar, three-dimensional spacetime experienced by observers isn’t a foundational aspect of reality, but rather a constructed phenomenon arising from the interaction of simpler, one-dimensional universes. This construction occurs through a process termed the ‘Knitting Mechanism’, wherein these fundamental, lower-dimensional entities are linked and interwoven. Imagine these one-dimensional universes as individual threads; the Knitting Mechanism acts as a series of algebraic operations – specifically, symmetry breaking within a W_3 algebra – that bind these threads together. This isn’t a physical gluing, but a mathematical one, where the interactions create higher-dimensional structures. Crucially, the properties of our observed universe – its dimensionality, its constants, and even its laws of physics – are not predetermined, but emerge as consequences of how these one-dimensional universes are knitted together, offering a potential resolution to the challenges in reconciling quantum gravity with cosmological observations.
Algebraic Foundations: The Geometry of Existence
The Multiverse Model’s mathematical framework is fundamentally based on Jordan algebra, a non-associative algebraic structure exhibiting properties crucial for representing the model’s complex interactions. Specifically, the model extends this algebra to encompass the exceptional Jordan algebra H_3(\mathbb{C}) – the Hermitian matrices of size 3 over the complex numbers – and H_3(\mathbb{O}), utilizing octonions instead of complex numbers. This extension is necessary to accommodate the higher-dimensional spaces and non-commutative geometries inherent in the Multiverse Model’s representation of spacetime and inter-universe connections, providing a consistent mathematical basis for calculations involving wormhole topologies and condensate behavior.
Virasoro constraints are implemented within the Multiverse Model to guarantee the mathematical consistency and physical stability of the quantum condensate representing spacetime. These constraints, derived from the infinite-dimensional Virasoro algebra, impose restrictions on the allowed energy and momentum states of fluctuations within the condensate. Specifically, they enforce that the energy-momentum tensor, T_{\mu\nu}, remains bounded and well-behaved at the Planck length, preventing divergences and ensuring a stable ground state. This stabilization is crucial because the condensate forms the basis for the Wormhole Web, and uncontrolled fluctuations would lead to topological instabilities and a breakdown of the spacetime structure. The implementation involves imposing specific operator product expansion (OPE) conditions, effectively regulating the high-energy behavior of the quantum fields and maintaining unitarity.
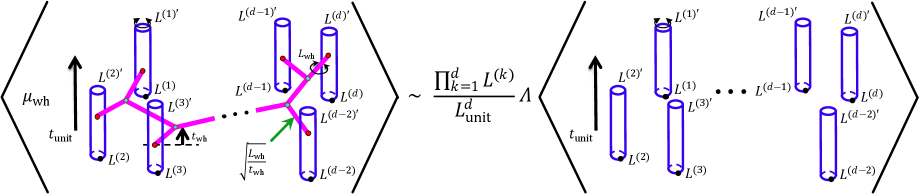
The ‘Wormhole Web’ is posited as the fundamental discretization of spacetime at the Planck\, Length \approx 1.6 \times 10^{-{35}} \, \text{meters}. Its configuration is not arbitrary; the ‘Virasoro Constraints’ mathematically restrict the permissible connectivity and arrangement of these wormholes. Specifically, these constraints ensure the resulting spacetime manifold remains well-defined and avoids singularities at this scale. Deviations from these allowed configurations lead to instability and a breakdown of the condensate forming the spacetime fabric. The constraints effectively define a set of allowed topological configurations for the wormhole network, dictating the permissible paths and connections at the Planck\, Length.
Resolving Cosmic Tensions: A New Friedmannian Landscape
The model posits a deviation from the standard Friedmann equations, which describe the expansion of the universe based on General Relativity. The resulting ‘Modified Friedmann Equation’ incorporates quantum effects arising from the proposed wormhole web structure and associated quantum weight. This modification alters the relationship between the universe’s energy density, pressure, and expansion rate, expressed mathematically as H^2 = (\frac{\dot{a}}{a})^2 = \frac{8\pi G}{3} \rho - \frac{k}{a^2} + Q , where H is the Hubble parameter, a the scale factor, ρ the energy density, k the curvature constant, and Q represents the quantum correction term derived from the wormhole structure. This altered equation is fundamental to the model’s predictions regarding accelerated expansion and the resolution of cosmological tensions.
The model’s Modified Friedmann Equation accounts for the observed late-time accelerated expansion of the universe without requiring a cosmological constant, Λ. Instead, the equation incorporates a quantum weight derived from the underlying wormhole web structure. This weight functions similarly to Λ in the standard ΛCDM model, driving the accelerating expansion, but originates from quantum gravitational effects rather than a vacuum energy density. Consequently, the model posits that the effective cosmological constant is not a fundamental constant of nature, but a dynamical quantity arising from the quantum properties of spacetime geometry, effectively reinterpreting Λ as a consequence of the wormhole web’s influence on the universe’s expansion rate.
The model addresses the Hubble Tension, a significant discrepancy between local measurements of the Hubble Constant (H_0) derived from Type Ia supernovae and Cepheid variables, and those inferred from observations of the Cosmic Microwave Background (CMB) by the Planck satellite. Current local measurements yield a value around 73-74 km/s/Mpc, while Planck data suggests approximately 67.4 km/s/Mpc. This model proposes a mechanism where the wormhole web structure and associated quantum weight effects introduce a time-varying deceleration parameter, effectively altering the relationship between redshift and distance. This alteration leads to predictions that reconcile the locally measured H_0 with CMB observations, potentially resolving the tension without requiring new physics beyond the framework of modified gravity and quantum effects on cosmological scales.
The model posits an initial state of exceptionally low entropy originating from the geometric structure of a proposed ‘Wormhole Web’. This initial condition is quantitatively consistent with a ratio of 10^{60} between current cosmological parameters – time, size, and matter energy – and their corresponding Planck units. Specifically, the current age of the universe, the observable universe’s diameter, and the total matter-energy density are all approximately 10^{60} times larger than their Planck-scale counterparts, suggesting a remarkably specific and low-probability initial configuration dictated by the wormhole network’s topology. This ratio is not predicted by standard cosmological models and serves as a key, testable prediction of this framework regarding the universe’s earliest moments.
Towards a Quantum Geometry: Future Directions and Theoretical Convergence
This research demonstrates a compelling synergy with Causal Dynamical Triangulations (CDT), a non-perturbative approach to quantum gravity that attempts to define a path integral over spacetimes. Crucially, CDT naturally extends to a W_3W_3 algebra, a powerful mathematical framework for describing two-dimensional conformal field theories. The present work, while distinct in its methodology, offers complementary insights into this same algebraic structure, suggesting a broader consistency within the landscape of quantum gravity theories. By approaching spacetime from an algebraic perspective, researchers can potentially bridge the gap between discrete, fundamental building blocks – as explored in CDT – and the smooth, continuous spacetime described by general relativity, ultimately leading to a more complete and unified understanding of gravity at the quantum level.
The observed correspondence between this work and Causal Dynamical Triangulations (CDT) offers a compelling avenue toward resolving the long-standing challenge of formulating a fully quantum theory of gravity. Existing attempts often falter when reconciling general relativity – the classical description of gravity – with the principles of quantum mechanics. However, the shared mathematical structure with CDT, particularly its extension to a W_3^{(3)} algebra, hints at a consistent framework where spacetime itself emerges from underlying quantum principles. This connection doesn’t merely provide a mathematical link; it suggests that the algebraic relationships defining spacetime’s structure at the Planck scale could be fundamental, potentially resolving divergences and singularities that plague conventional quantum gravity theories. The implication is a universe where gravity isn’t a force within spacetime, but rather a consequence of its underlying quantum algebraic geometry, offering a path towards a complete and self-consistent description of the cosmos at its most fundamental level.
Ongoing investigations are dedicated to meticulously refining the presented model, with a particular emphasis on its capacity to accurately describe the extreme gravitational environments surrounding black holes. Researchers aim to leverage the model’s algebraic framework to probe the singularity at the heart of these cosmic entities and to better understand the information paradox. Simultaneously, exploration extends to the very earliest moments of the universe, investigating whether the model can provide insights into the initial conditions of the Big Bang and the subsequent inflationary epoch. By applying the model’s predictive power to these cosmological frontiers, scientists hope to unveil connections between quantum gravity and the observed large-scale structure of the cosmos, potentially offering a novel perspective on the universe’s origin and evolution.
The prevailing view of spacetime as a smooth continuum may ultimately give way to a description rooted in abstract algebraic structures. This emerging perspective posits that the fundamental properties of the cosmos – its geometry, topology, and even the laws governing particle interactions – are not inherent features of space itself, but rather consequences of underlying algebraic relations. Researchers anticipate that by meticulously mapping physical phenomena onto these structures, a deeper and more unified understanding of gravity and quantum mechanics can be achieved. This algebraic framework promises not only a resolution to long-standing theoretical inconsistencies, but also a novel approach to cosmology, potentially revealing insights into the very origins and ultimate fate of the universe, and offering a mathematically elegant description of phenomena ranging from black hole singularities to the inflationary epoch following the Big Bang.
The exploration of multiverse models, as presented in this work, inherently acknowledges the transient nature of any proposed system. Each universe, born from the symmetry breaking of the W3 algebra and interconnected via the ‘knitting’ mechanism, represents a temporary configuration within a larger, evolving framework. This resonates with the assertion that “Anything goes.” Paul Feyerabend’s pronouncement isn’t a dismissal of rigor, but an acknowledgment that methodological constraints themselves are subject to decay. The study’s approach, while deeply mathematical, implicitly recognizes that even the most elegant theories-like those attempting to resolve the cosmological constant problem-are provisional, destined to be refined or replaced as understanding evolves. Every failure, in this context, is a signal from time, guiding the search for more robust descriptions of reality.
The Loom Unwinds
The proposition that our universe arises as a localized symmetry breaking within a larger multicomponent W3 algebra, linked to Jordan algebras, feels less a resolution than a careful relocation of the problem. The cosmological constant, a persistent irritant, is not vanquished, merely explained away as a consequence of the multiverse’s internal dynamics. Every abstraction carries the weight of the past; this model, however elegant, inherits the questions surrounding the initial conditions of the encompassing algebraic structure. The ‘knitting mechanism’, invoking wormholes, is conceptually appealing, but readily concedes the inherent limitations in probing connections beyond our observable horizon.
Future work will inevitably focus on quantifying the stability of these wormhole networks and exploring the statistical distribution of universes within this multiverse. A crucial, and likely intractable, challenge lies in devising testable predictions. Any observable signature of another universe, however faint, will be subject to the inherent ambiguity of interpreting signals across such vast cosmological distances. The Friedmann equation, a cornerstone of the analysis, remains anchored in our local physics – its applicability to universes governed by different algebraic components is an assumption, not a certainty.
Ultimately, the enduring value of such investigations lies not in achieving definitive answers, but in refining the questions. Only slow change preserves resilience. This framework, while ambitious, serves as a poignant reminder that every model is a temporary scaffolding erected against the inevitable decay of understanding. The loom unwinds, and the pattern, however intricate, is destined to fray.
Original article: https://arxiv.org/pdf/2601.10499.pdf
Contact the author: https://www.linkedin.com/in/avetisyan/
See also:
- Darkwood Trunk Location in Hytale
- Best Controller Settings for ARC Raiders
- Hytale: Upgrade All Workbenches to Max Level, Materials Guide
- Ashes of Creation Rogue Guide for Beginners
- Daredevil Is Entering a New Era With a Chilling New Villain (And We Have A First Look) (Exclusive)
- We’ll Never Get Another Star Wars Show Like Andor, But Not Because of Dave Filoni
- RHOBH’s Jennifer Tilly Reacts to Sutton Stracke “Snapping” at Her
- Katy Perry Shares Holiday Pics With Justin Trudeau & Ex Orlando Bloom
- So Long, Anthem: EA’s Biggest Flop Says Goodbye
- 7 Announcements We’re Dying to See at Dragon Ball’s Genki Dama Festival This Month
2026-01-17 21:10