Unconventional Magnetism Powers Superconducting Diodes

Author: Denis Avetisyan

New research demonstrates a highly efficient superconducting diode effect arising from the interplay of unconventional magnetism and superconductivity, opening doors to next-generation energy-saving electronics.

The efficiency of the stochastic differential equation in realizing a spin-singlet dd-wave phase-modulated along the direction of minimal wave vector <span class="katex-eq" data-katex-display="false">\mathbf{Q}</span>-exhibits a dependence on the upper polar moment spin splitting λ, particularly under a magnetic field normalized to the critical temperature, and this relationship varies predictably with temperature itself. — The efficiency of the stochastic differential equation in realizing a spin-singlet dd-wave phase-modulated along the direction of minimal wave vector $\mathbf{Q}$ -exhibits a dependence on the upper polar moment spin splitting λ, particularly under a magnetic field normalized to the critical temperature, and this relationship varies predictably with temperature itself.

The study explores the emergence of superconductivity in materials with odd-parity magnetism, leveraging the Fulde-Ferrell state and proximity effects to achieve a significant diode effect.

Conventional superconductivity relies on established pairing mechanisms, yet recent theoretical proposals suggest unconventional magnetism could host novel superconducting states. This work, titled ‘Highly efficient superconducting diode effect in unconventional $p$-wave magnets’, explores the emergence of such superconductivity in materials with odd-parity magnetism, revealing a pathway to highly efficient superconducting diodes. Through Ginzburg-Landau theory, we demonstrate that significant efficiencies are achievable under experimentally relevant conditions, potentially enabling energy-saving logic circuits. Could these findings pave the way for a new generation of low-power electronic devices for both classical and quantum computation?

Order from the Shadows: Rethinking Conventional Magnetism

For generations, magnetism has been visualized as arising from the cooperative alignment of atomic magnetic moments – a simple, parallel ordering that generates familiar fields. However, a burgeoning field of materials science is revealing systems where this foundational principle breaks down. These materials, often complex oxides and intermetallic compounds, demonstrate magnetic order without requiring such straightforward alignment. Instead, moments can arrange in more intricate patterns – spirals, cones, or even completely disordered states – that still yield macroscopic magnetic behavior. This departure from conventional magnetism isn’t merely a curiosity; it hints at previously unrecognized interactions and symmetries governing magnetic phenomena, opening doors to potential applications in data storage, spintronics, and beyond, and fundamentally reshaping the understanding of magnetic order itself.

The conventional picture of magnetism, where atomic moments align in parallel or antiparallel fashion, is increasingly being overturned by the discovery of unconventional magnetic states. These states arise from complex arrangements of magnetic moments that are not simply aligned, but instead adopt non-collinear configurations – spiraling, twisting, or forming more intricate patterns. This departure from traditional magnetic order fundamentally challenges existing theoretical frameworks, demanding a re-evaluation of how magnetic interactions give rise to macroscopic properties. Researchers are discovering that these non-collinear arrangements aren’t merely deviations from the norm, but rather represent entirely new phases of matter with potentially groundbreaking applications, from advanced data storage to novel spintronic devices. The exploration of these complex magnetic textures is therefore driving a vibrant field of materials science, pushing the boundaries of what is known about magnetic order and its underlying principles.

The emergence of unconventional magnetism isn’t merely a deviation from established principles; it unveils a landscape where material properties are dictated by subtle symmetry considerations. These materials, unlike those exhibiting simple ferromagnetic order, demonstrate behaviors – such as topologically protected spin textures and unusual responses to external fields – directly linked to the underlying crystal symmetry and the interplay between spin, charge, and orbital degrees of freedom. Consequently, traditional theoretical frameworks, designed for systems with straightforward magnetic ordering, prove inadequate. Researchers are now compelled to develop novel approaches – often involving complex mathematical formalisms and advanced computational techniques – to accurately describe and predict the exotic properties arising from these unique symmetry-driven magnetic states, potentially paving the way for groundbreaking advancements in spintronics and materials science.

In a UPM, an out-of-plane magnetic field <span class="katex-eq" data-katex-display="false"> \mathbf{B}=B_{z}\bm{\hat{z}} </span> induces spin splitting of the Fermi surfaces (shown in red and blue for <span class="katex-eq" data-katex-display="false"> \langle\sigma_{z}\rangle=\pm\hbar/2 </span>), displaces them from the zone center by <span class="katex-eq" data-katex-display="false"> \mathbf{k}_{0}=2\frac{m\lambda}{\hbar^{2}}\bm{\hat{x}} </span>, and suppresses the nodes up to a critical field of <span class="katex-eq" data-katex-display="false"> B_{c}=\pm\absolutevalue{\lambda}\sqrt{\frac{2m\mu}{\hbar^{2}}} </span>, while any in-plane field results in nodeless Fermi surfaces. — In a UPM, an out-of-plane magnetic field $\mathbf{B}=B_{z}\bm{\hat{z}}$ induces spin splitting of the Fermi surfaces (shown in red and blue for $\langle\sigma_{z}\rangle=\pm\hbar/2$ ), displaces them from the zone center by $\mathbf{k}_{0}=2\frac{m\lambda}{\hbar^{2}}\bm{\hat{x}}$ , and suppresses the nodes up to a critical field of $B_{c}=\pm\absolutevalue{\lambda}\sqrt{\frac{2m\mu}{\hbar^{2}}}$ , while any in-plane field results in nodeless Fermi surfaces.

Zero Sum: The Paradox of pp-Wave Magnetism

pp-wave magnetism is characterized by a unique magnetic ordering where individual atomic magnetic moments are non-zero, yet the material exhibits zero net magnetization. This counterintuitive behavior stems from the specific spatial arrangement and alignment of these moments; instead of summing constructively to produce a macroscopic magnetic field, the moments are configured in a manner that results in complete cancellation. This does not imply the absence of magnetic interactions, but rather a cancellation of magnetic dipole contributions at the macroscopic level, differentiating pp-wave magnetism from conventional ferromagnetic or antiferromagnetic materials where net magnetization arises from aligned or oppositely aligned moments, respectively.

Odd-parity spin splitting in pp-wave magnetism refers to a non-collinear arrangement of magnetic moments where the direction of each moment is perpendicular to its associated spin-orbit coupling. This splitting, and the resulting zero net magnetization, is directly correlated with the breaking of inversion symmetry within the material’s crystal structure. Without inversion symmetry, the $k$ -dependent spin splitting allows for the cancellation of magnetic moments, even when individual moments possess non-zero magnitude. This mechanism contrasts with conventional ferromagnetism, where symmetry allows for a net magnetic moment. The degree of spin splitting, and therefore the suppression of magnetization, is determined by the strength of the symmetry breaking and the electronic band structure.

Unconventional magnetic orders, such as those observed in pp-wave magnetism, are stabilized by composite symmetries that combine spatial symmetries with the translation operator. These symmetries dictate the allowed magnetic configurations and can be leveraged to control magnetic properties via external stimuli. The breaking or modification of these composite symmetries can induce a transition to a superconducting state characterized by finite momentum pairing, $\mathbf{q}$ . This finite-momentum superconductivity, distinct from conventional zero-momentum superconductivity, has the potential to enable the creation of highly efficient electronic devices with novel functionalities, due to reduced energy dissipation and potentially higher operating temperatures.

The critical temperatures of chiral <span class="katex-eq" data-katex-display="false">pp</span>-wave and helical <span class="katex-eq" data-katex-display="false">pp</span>-wave pairing states depend on the UPM splitting λ, with the chiral state remaining unaffected and a zero-momentum state emerging only in the helical phase for finite λ, which is suppressed but persists even as λ approaches infinity. — The critical temperatures of chiral $pp$ -wave and helical $pp$ -wave pairing states depend on the UPM splitting λ, with the chiral state remaining unaffected and a zero-momentum state emerging only in the helical phase for finite λ, which is suppressed but persists even as λ approaches infinity.

The Architectures of Instability: Ginzburg-Landau and Beyond

The Ginzburg-Landau theory is a phenomenological framework used to describe phase transitions in condensed matter physics, notably superconductivity and magnetism. It posits that near a critical temperature, the order parameter – which quantifies the degree of order in the phase – can be treated as a complex-valued field. The theory utilizes a free energy functional, typically expressed as an expansion in powers of the order parameter and its spatial derivatives, to determine the stable phases and their properties. This functional includes terms representing the condensation energy, the gradient energy, and any external fields. By minimizing this free energy, the theory predicts the emergence of spatial variations in the order parameter, leading to phenomena like vortex formation in superconductors and domain structures in magnetic materials. The power of the theory lies in its ability to provide a unified description of different phase transitions using a common mathematical structure, although it does not derive the microscopic origins of these phenomena.

The application of Ginzburg-Landau theory to unconventional magnetic systems requires modifications beyond the standard formulation due to the significant role of spin-orbit coupling and the frequent presence of symmetry-breaking terms. Spin-orbit coupling, arising from the interaction between an electron’s spin and its orbital motion, introduces anisotropic interactions and modifies the electronic band structure, impacting the free energy functional used in the theory. Furthermore, many unconventional magnets exhibit reduced symmetry compared to conventional systems; therefore, terms describing these broken symmetries, such as those arising from Dzyaloshinskii-Moriya interactions or magnetic anisotropy, must be explicitly included in the Ginzburg-Landau free energy to accurately describe the magnetic order and phase transitions. These additions expand the order parameter space and necessitate careful consideration of the resulting symmetry constraints when analyzing the stability of various magnetic phases.

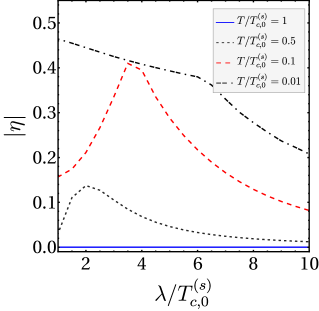
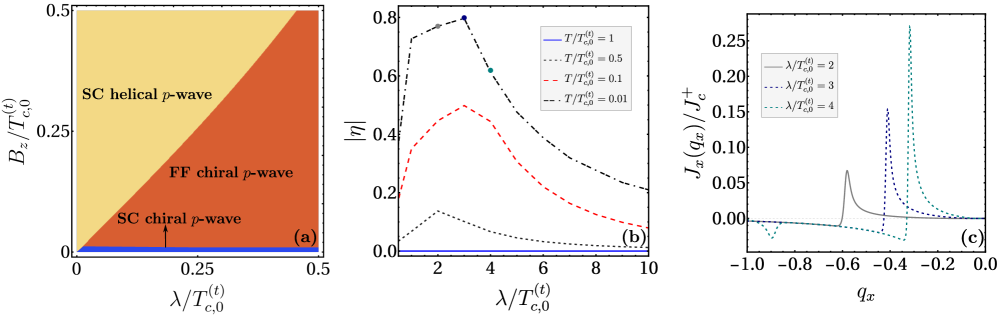
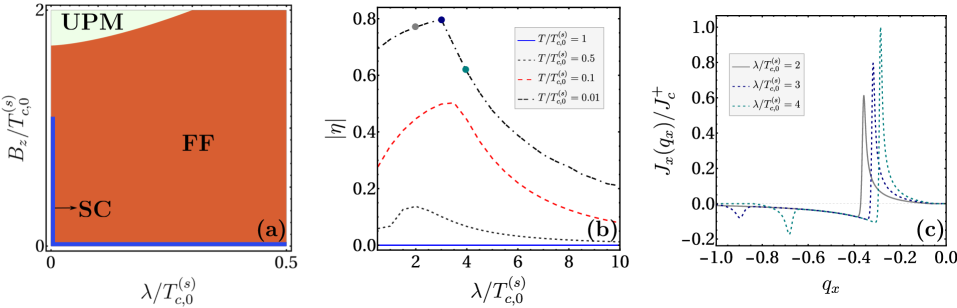
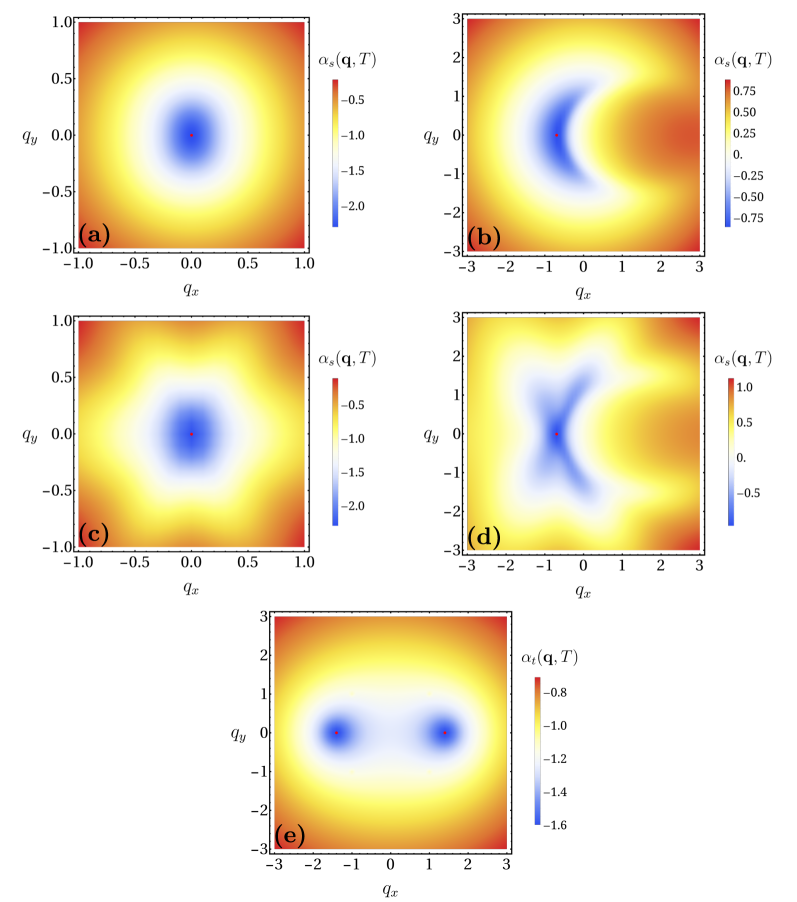
Within the Ginzburg-Landau framework, the Digamma function is crucial for calculating thermodynamic properties and predicting critical temperatures for both superconducting and magnetic phase transitions. Specifically, its application to the free energy minimization allows determination of stable phases and associated order parameters as a function of temperature and external fields. Recent modeling utilizing this approach has demonstrated the potential for achieving superconducting diode efficiencies of approximately 80% under specific conditions. These optimal parameters include a controlled degree of UPM (Up-Down Modulation) splitting and operation at low temperatures, suggesting a pathway towards rectifying current flow in superconducting circuits. The precise value of the critical temperature, and therefore the efficiency, is highly dependent on material parameters incorporated into the Digamma function calculations.

The model’s pairing phase diagram exhibits an efficiency η modulated by spin splitting λ and temperature, peaking at specific values that correlate with enhanced supercurrent at low temperatures.

Beyond Equilibrium: The Emergence of Novel Functionality

In certain unconventional superconducting materials, superconductivity isn’t limited to zero momentum; instead, Cooper pairs can acquire a finite momentum, leading to a spatially modulated state known as a pair density wave (PDW). This occurs when the Fermi surface possesses specific characteristics that favor a non-zero center-of-mass momentum for the paired electrons. The resulting PDW isn’t a uniform superconducting state, but rather one where the superconducting gap, and therefore the density of Cooper pairs, oscillates in space. These oscillations create a periodic modulation of the electronic properties, altering the material’s behavior and potentially giving rise to novel effects, such as anisotropic conductivity and, crucially, the possibility of realizing a superconducting diode – a device that conducts electricity preferentially in one direction. The formation of PDWs represents a departure from conventional Bardeen-Cooper-Schrieffer (BCS) theory and opens pathways to explore exotic superconducting phenomena.

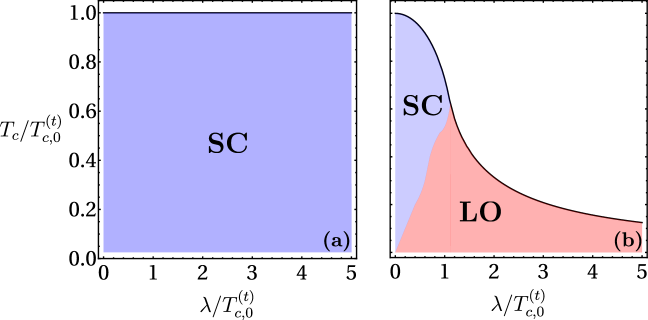
Unconventional superconductors, beyond the traditional understanding of electron pairing, give rise to modulated pairing states with strikingly unique electronic behaviors. These states, where the superconducting gap varies spatially, aren’t simply about zero resistance; they unlock the possibility of a superconducting diode effect, enabling current to flow preferentially in one direction – a feat previously thought impossible. The critical temperature $T_c$ at which this superconductivity emerges isn’t fixed, but rather intimately tied to the symmetry of the electron pairing and the influence of applied magnetic fields. Specifically, helical $pp$ -wave pairing experiences a mild reduction in $T_c$ under these conditions, while chiral $pp$ -wave pairing remains remarkably robust, suggesting a pathway towards designing superconductors with tailored directional current flow and enhanced stability.

Beyond conventional superconductivity, certain materials exhibit fascinating states driven by competing interactions, notably the Fulde-Ferrell (FF) and Larkin-Ovchinnikov (LO) phases. These phases arise when Cooper pairs, typically possessing zero momentum, acquire a finite momentum due to strong magnetic fields or spatially varying potentials. In the FF state, Cooper pairs condense with a specific, non-zero momentum, forming a spatially modulated superconducting state; the LO phase, meanwhile, creates a periodic modulation of the superconducting order parameter in real space. These modulated states are not merely theoretical curiosities; they dramatically alter the material’s electronic properties, influencing the critical temperature and potentially leading to exotic phenomena like anisotropic superconductivity and the aforementioned superconducting diode effect – a clear departure from the symmetry-protected behavior of conventional superconductors. Understanding these phases is therefore crucial for designing novel superconducting devices and unlocking the full potential of unconventional superconductivity.

The efficiency of the stochastic differential equation for the fluctuating force phase, maximized along the minimizing wave vector <span class="katex-eq" data-katex-display="false">\mathbf{Q}</span>, exhibits a temperature-dependent peak as a function of spin splitting λ, influencing the resulting supercurrent behavior at low temperatures. — The efficiency of the stochastic differential equation for the fluctuating force phase, maximized along the minimizing wave vector $\mathbf{Q}$ , exhibits a temperature-dependent peak as a function of spin splitting λ, influencing the resulting supercurrent behavior at low temperatures.

Reframing the Search: Towards Predictive Materials Design

The inherent complexity of real-world materials often necessitates simplification when modeling their behavior at a fundamental level. Researchers increasingly turn to two-dimensional models as a powerful tool to dissect intricate interactions within materials. By reducing dimensionality, these models allow for the construction of detailed Hamiltonians – mathematical descriptions of the total energy of the system – that would be intractable in three dimensions. These Hamiltonians, built upon approximations yet retaining essential physics, enable precise calculations of electronic structure and magnetic properties. This approach not only provides valuable insights into the behavior of existing materials, but also serves as a crucial stepping stone for predicting and designing novel materials with tailored characteristics. The ability to perform these detailed calculations is paramount in the quest to understand and harness the potential of quantum materials.

Calculations demonstrate that Rashba spin-orbit coupling is a fundamental mechanism influencing the behavior of electrons within these systems. This interaction, arising from the interplay between an electron’s spin and its motion within an electric field, introduces anisotropic interactions and modifies the electronic band structure, impacting the free energy functional used in the theory. Consequently, this reshaping isn’t merely a structural change; it actively drives unconventional magnetic phenomena. Unlike traditional magnetism stemming from aligned electron spins, the Rashba effect fosters more complex magnetic orderings, potentially leading to novel magnetic textures and functionalities. The strength of this coupling, and its influence on the electronic structure, provides a crucial pathway towards designing materials with tailored magnetic properties and exploring previously unattainable states of matter – potentially revolutionizing spintronics and quantum computing.

The pursuit of materials exhibiting these newly understood exotic quantum states represents a significant frontier in condensed matter physics. Researchers are actively investigating a diverse range of material candidates, from tailored heterostructures to novel topological semimetals, with the aim of realizing and controlling these effects. Beyond fundamental discovery, a key focus lies in manipulating material properties – such as composition, strain, and dimensionality – to enhance and stabilize these states for practical applications. This includes exploring their potential in spintronics, quantum computing, and the development of low-power electronic devices, promising a pathway from theoretical understanding to tangible technological innovation.

The second-order coefficient of the Ginzburg-Landau free energy, calculated at <span class="katex-eq" data-katex-display="false">T=0.1T_{c,0}^{(s)}</span> and <span class="katex-eq" data-katex-display="false">\lambda/T_{c,0}^{(s)}=1</span>, reveals distinct minima for ss- and dd-wave states at <span class="katex-eq" data-katex-display="false">B/T_{c,0}^{(s)}=0</span> and <span class="katex-eq" data-katex-display="false">B/T_{c,0}^{(s)}=1</span>, with the latter exhibiting a single minimum at <span class="katex-eq" data-katex-display="false">\mathbf{Q}=-0.7\widehat{\mathbf{x}}</span>, while the helical pp-wave state displays two minima related by a <span class="katex-eq" data-katex-display="false">C_{2z}</span> rotation. — The second-order coefficient of the Ginzburg-Landau free energy, calculated at $T=0.1T_{c,0}^{(s)}$ and $\lambda/T_{c,0}^{(s)}=1$ , reveals distinct minima for ss- and dd-wave states at $B/T_{c,0}^{(s)}=0$ and $B/T_{c,0}^{(s)}=1$ , with the latter exhibiting a single minimum at $\mathbf{Q}=-0.7\widehat{\mathbf{x}}$ , while the helical pp-wave state displays two minima related by a $C_{2z}$ rotation.

The exploration of unconventional superconductivity, as detailed in this work, reveals a system where order isn’t imposed, but arises from the interplay of local magnetic and superconducting properties. This mirrors the principle that complex systems benefit more from encouraging local rules than building rigid hierarchies. As Karl Popper observed, “The more a theory tries to explain, the more it necessarily explains away.” In this research, the focus on odd-parity magnetism and proximity effects doesn’t attempt a complete, overarching explanation of superconductivity, but rather investigates how local conditions can give rise to emergent phenomena – specifically, a highly efficient superconducting diode effect. System outcomes remain unpredictable, yet demonstrably resilient, showcasing the power of bottom-up emergence over top-down control.

Beyond Directionality

The demonstration of a robust superconducting diode effect within unconventional magnetic systems suggests a path toward electronics where dissipation is not an inherent cost. However, to speak of ‘efficiency’ implies a goal, an intended outcome. The system simply is; the directionality emerges from the interplay of established phases, not through deliberate design. The effect of the whole is not always evident from the parts, and attempts to engineer such phenomena with granular control may prove… optimistic. A more fruitful approach might lie in identifying materials where these effects are intrinsic, accepting the limitations of imposed order.

The current work, while promising, remains constrained by theoretical models – Ginzburg-Landau theory, for instance – that, while powerful, are ultimately approximations. The subtleties of odd-parity pairing, particularly in proximity to complex magnetic textures, likely harbor unexplored phases and effects. Further investigation into the Fulde-Ferrell state and its potential for tunable anisotropy could unlock even more sophisticated device functionalities, though controlling such states remains a significant hurdle.

Perhaps the most compelling direction lies in shifting the focus from ‘building’ such devices to ‘observing’ their emergence. The universe rarely conforms to preconceived notions of optimization. Sometimes it’s better to observe than intervene, to allow complexity to self-organize and reveal its inherent properties. The pursuit of unconventional superconductivity, then, becomes less about achieving a desired outcome and more about understanding the principles that govern the emergence of order itself.

Original article: https://arxiv.org/pdf/2601.09783.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/