Whispers Between Billiards: How System Coupling Shapes Quantum Chaos

Author: Denis Avetisyan

New research demonstrates that even subtle connections between quantum systems exhibiting predictable and unpredictable behavior fundamentally alter their spectral fingerprints.

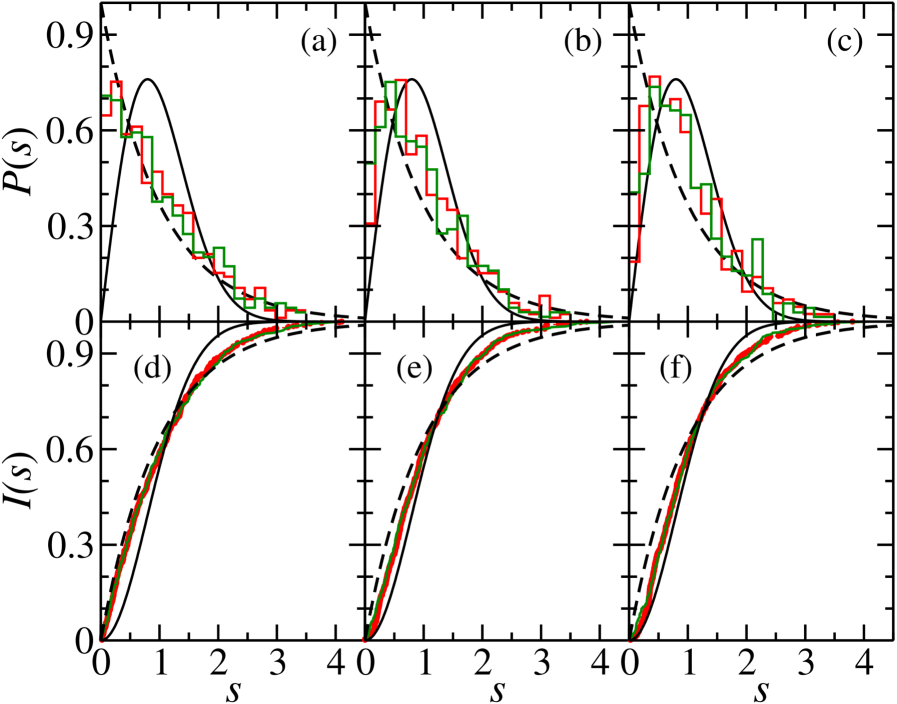
The study demonstrates how the distribution of nearest-neighbor spacing, quantified by <span class="katex-eq" data-katex-display="false"> P(s) </span> and its cumulative form <span class="katex-eq" data-katex-display="false"> I(s) </span>, transitions from Poissonian behavior for weakly coupled systems to characteristics mirroring Gaussian Orthogonal Ensemble (GOE) random matrices with increasing coupling strength, as validated by a comparison between experimental data and COMSOL Multiphysics computations. — The study demonstrates how the distribution of nearest-neighbor spacing, quantified by $P(s)$ and its cumulative form $I(s)$ , transitions from Poissonian behavior for weakly coupled systems to characteristics mirroring Gaussian Orthogonal Ensemble (GOE) random matrices with increasing coupling strength, as validated by a comparison between experimental data and COMSOL Multiphysics computations.

Experimental investigation of coupled quantum billiards validates a modified Rosenzweig-Porter random matrix model for describing the resulting spectral properties.

Understanding how quantum systems transition between integrable and chaotic behaviors remains a central challenge in quantum physics. This is addressed in ‘Experimental study of coupled quantum billiards with integrable and chaotic classical dynamics and test of a special Rosenzweig-Porter model’, which experimentally investigates the spectral properties of coupled quantum billiards – one exhibiting integrable, the other chaotic dynamics. Our findings demonstrate that even weak coupling significantly alters these spectral characteristics, driving the system away from purely integrable or chaotic behavior and allowing for quantification via a modified Rosenzweig-Porter random matrix model. Could this approach offer a new pathway for characterizing and predicting the behavior of complex quantum systems with interacting components?

The Delicate Dance Between Order and Chaos

The shift from order to chaos represents a core puzzle in physics, impacting fields from celestial mechanics to fluid dynamics. Historically, deterministic systems – those where the future is, in theory, fully determined by initial conditions – were assumed to always follow predictable trajectories. However, investigations revealed that even simple deterministic systems can exhibit extreme sensitivity to those initial conditions, a phenomenon popularly known as the “butterfly effect”. This sensitivity manifests as chaotic behavior, where minuscule changes at the start lead to wildly divergent outcomes. Understanding when and how this transition from stable, predictable dynamics – termed ‘integrable’ – to chaotic behavior occurs is thus a central goal, requiring physicists to identify the underlying mechanisms that govern this delicate balance and to develop tools for characterizing the nature of chaos itself. The challenge isn’t simply observing randomness, but pinpointing the precise conditions that allow it to emerge from deterministic rules.

Quantum billiards represent a powerful theoretical framework for investigating the interplay between order and chaos by modeling the behavior of quantum waves confined within specifically shaped boundaries. These idealized systems, often visualized as a particle bouncing around inside a geometric container, allow physicists to meticulously control the system’s defining characteristics – the shape of the boundary and the energy of the wave. By altering these parameters, researchers can observe a clear progression from predictable, regular wave patterns – analogous to a perfectly ordered billiard game – to increasingly complex and erratic behavior indicative of quantum chaos. This controlled environment is crucial, as it simplifies the analysis of complex quantum phenomena and provides a direct link between the system’s classical geometry and its resulting quantum signatures, enabling a deeper understanding of how chaos manifests at the quantum level and offering insights into the broader field of quantum dynamics.

The correspondence between classical and quantum mechanics becomes strikingly apparent when examining quantum billiards. Integrable classical systems – those where trajectories remain predictable and confined – translate to quantum systems exhibiting highly regular energy spectra and wave patterns, often displaying characteristic ‘whispering gallery’ modes where waves circulate repeatedly without decay. Conversely, chaotic classical billiards, where particle paths diverge exponentially, manifest in quantum systems as significantly different behavior; their energy spectra become disordered and exhibit statistical properties consistent with random matrix theory. This means that the seemingly simple act of changing the shape of the billiard table – transitioning from a perfect circle or ellipse to a more complex, irregular form – dramatically alters the quantum wavefunction’s behavior, blurring the lines between predictable and unpredictable quantum states and offering a powerful demonstration of how classical chaos leaves a distinct fingerprint on the quantum realm.

The semicircular (red) and chaotic (blue) portions of the spectrum closely match analytical eigenvalue predictions, demonstrating the accuracy of the model.

The Semicircle: A Bastion of Integrability

The semicircular quantum billiard system is advantageous for research due to the perfectly integrable dynamics exhibited by its classical analog. In classical mechanics, an integrable system possesses a sufficient number of conserved quantities – typically equaling the number of degrees of freedom – to allow for exact solutions of the equations of motion. This characteristic simplifies the analysis of the system’s behavior and provides a well-defined baseline for comparison with quantum mechanical results. The semicircular geometry, in particular, allows for analytical solutions in the classical limit, facilitating the identification of corresponding quantum phenomena and the study of deviations from integrability when perturbations are introduced.

Realization of the semicircular quantum billiard is achieved through the fabrication of a physical microwave resonator. This involves creating a precisely engineered structure capable of confining and controlling microwave photons, effectively mimicking the behavior of a quantum particle within the semicircular potential well. The resonator’s geometry is critical, as deviations from the ideal semicircle impact the system’s integrability. Fabrication techniques allow for the creation of resonators with dimensions on the order of millimeters, enabling experimental investigation of quantum phenomena at accessible scales. This physical implementation provides a platform for directly observing and quantifying the quantum behavior predicted by theoretical models of the billiard system.

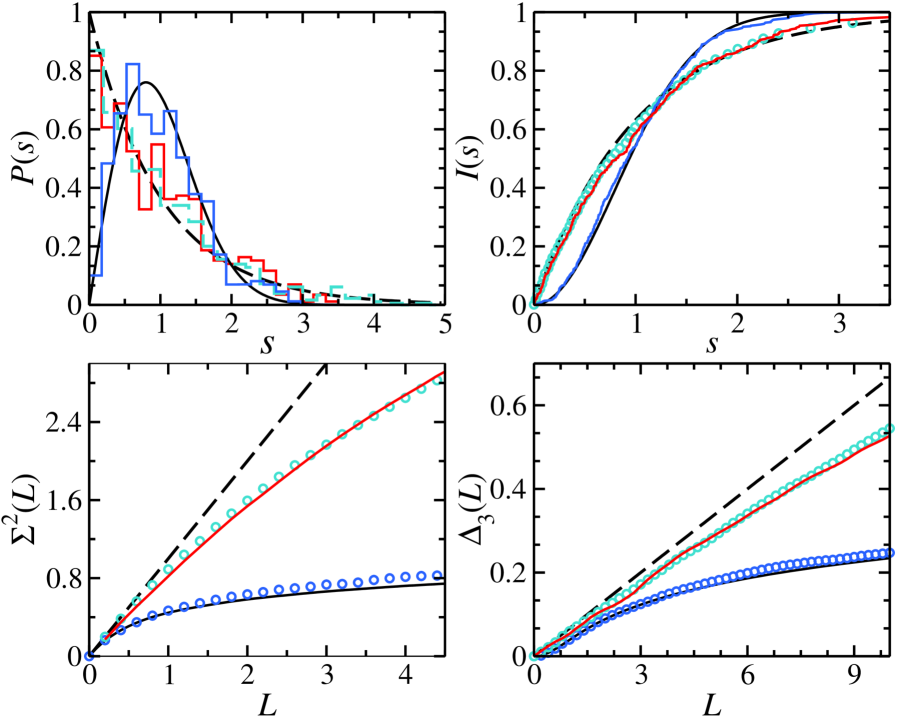
Tunable parameters within the semicircular quantum billiard system, specifically ‘slit coupling,’ enable investigation into the effects of non-integrability on quantum dynamics. The degree of coupling is quantitatively controlled, with established parameters of 0.03 representing weak coupling, 0.23 indicating moderate coupling, and 0.35 denoting strong coupling. These discrete coupling levels facilitate a systematic study of how deviations from perfectly integrable behavior-characterized by regular, predictable trajectories-manifest in the quantum realm, allowing for observation of phenomena such as the transition from regular to chaotic behavior and the resulting changes in energy level statistics and wavefunction characteristics.

Normalized wave function intensity distributions reveal that resonance frequencies <span class="katex-eq" data-katex-display="false">f_n</span> remain consistent across weakly, moderately, and strongly coupled configurations of a cavity containing circular niobium disks, with values of 8.50, 10.29, 9.10, and 11.08 GHz for the observed eigenmodes. — Normalized wave function intensity distributions reveal that resonance frequencies $f_n$ remain consistent across weakly, moderately, and strongly coupled configurations of a cavity containing circular niobium disks, with values of 8.50, 10.29, 9.10, and 11.08 GHz for the observed eigenmodes.

Decoding Chaos: Statistical Signatures and the Power of Random Matrices

Random Matrix Theory (RMT) posits that the statistical distribution of energy levels in complex quantum systems exhibiting chaotic behavior can be accurately modeled using the eigenvalues of random matrices. This approach bypasses the need to solve the often-intractable Schrödinger equation directly for these systems. Specifically, RMT predicts universal statistical properties, independent of the system’s microscopic details, focusing instead on symmetries like time-reversal invariance which dictate the appropriate ensemble of random matrices – typically the Gaussian Orthogonal Ensemble (GOE), Gaussian Symplectic Ensemble (GSE), or Gaussian Unitary Ensemble (GUE). The key prediction is the Wigner surmise, describing the short-range correlations of eigenvalues, and the associated distributions of level spacings which differ markedly from those found in integrable systems. The applicability of RMT rests on the assumption of quantum chaos, where classical chaotic trajectories are present in the corresponding classical system and the quantum mechanical wavefunctions are sufficiently delocalized.

The presence of quantum chaos is quantitatively assessed through statistical analysis of energy level spectra using metrics such as the Nearest-Neighbor Spacing Distribution (NNSD), Number Variance $\sigma^2$ , and Rigidity. NNSD describes the probability distribution of the spacing between adjacent energy levels; chaotic systems exhibit a characteristic Wigner surmise distribution, differing from the Poisson statistics expected for integrable systems. Number Variance, calculated as the variance of the number of energy levels within a given energy range, distinguishes between chaotic systems ( $\sigma^2 \approx 0.37$ ) and integrable systems ( $\sigma^2 = 0$ ). Rigidity measures the sensitivity of the number of levels to small energy window changes; chaotic systems display significantly higher rigidity compared to those that are integrable. Deviations from the predictions of Random Matrix Theory (RMT) for these metrics – specifically, observed values differing from those predicted by RMT – provide evidence for the presence, or absence, of underlying quantum chaos.

The Berry-Tabor Conjecture posits that the statistical distribution of energy levels in integrable quantum systems follows a Poisson distribution, characterized by a level spacing distribution exhibiting exponential decay. This contrasts directly with the predictions of Random Matrix Theory (RMT) for chaotic systems, which yield a Wigner surmise – a distribution approximated by a Gaussian Orthogonal Ensemble – resulting in a level repulsion effect and a significantly different level spacing distribution. Specifically, the Number Variance $\sigma^2$ for Poisson statistics is equal to 1, while RMT predictions for chaotic systems yield values substantially less than 1, indicating correlations between energy levels absent in integrable systems. The conjecture provides a quantifiable distinction: integrable systems lack the level repulsion characteristic of chaotic systems, evidenced by differing statistical properties of their energy spectra.

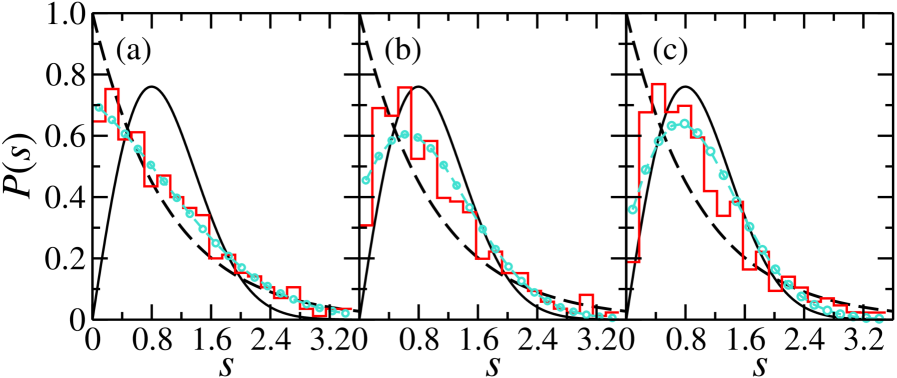
The distribution of nearest-neighbor spacing reveals a transition from Poisson statistics (dashed black line) to Gaussian Orthogonal Ensemble (GOE) behavior (solid black line) as coupling strength increases, with fitted Berry-Robnik parameters of <span class="katex-eq" data-katex-display="false">\mu=0.537817</span>, <span class="katex-eq" data-katex-display="false">\mu=0.770701</span>, and <span class="katex-eq" data-katex-display="false">\mu=0.846023</span> corresponding to weak, moderate, and strong coupling, respectively, as confirmed by comparison with experimental data (red histograms and turquoise fits). — The distribution of nearest-neighbor spacing reveals a transition from Poisson statistics (dashed black line) to Gaussian Orthogonal Ensemble (GOE) behavior (solid black line) as coupling strength increases, with fitted Berry-Robnik parameters of $\mu=0.537817$ , $\mu=0.770701$ , and $\mu=0.846023$ corresponding to weak, moderate, and strong coupling, respectively, as confirmed by comparison with experimental data (red histograms and turquoise fits).

Simulating and Realizing Quantum Chaos: A Convergence of Theory and Experiment

The intricate design and precise optimization of the microwave resonator, central to observing quantum chaos, relies heavily on advanced simulation software such as COMSOL Multiphysics. This software allows researchers to model the electromagnetic field distribution within the resonator with high fidelity, predicting resonant frequencies and mode shapes before physical fabrication. By virtually prototyping different geometries and material configurations, scientists can fine-tune the resonator to maximize the sensitivity to chaotic behavior and minimize unwanted effects like spurious resonances. The ability to accurately simulate these complex systems drastically reduces the time and resources needed for experimental iterations, enabling the creation of resonators specifically tailored to probe the transition from regular to chaotic quantum dynamics and validate theoretical predictions based on random matrix theory.

The Gaussian Orthogonal Ensemble (GOE) serves as a powerful statistical framework for understanding the energy levels of quantum systems exhibiting time-reversal symmetry – a condition frequently met in experimental setups involving microwave resonators and quantum billiards. This symmetry implies that for every quantum state, a corresponding state exists with reversed time direction, influencing the overall distribution of energy levels. The GOE predicts that the spacing between these energy levels will follow a characteristic distribution, distinct from that observed in systems lacking this symmetry. By comparing the observed energy level statistics with the predictions of the GOE, researchers can confirm the presence of time-reversal symmetry and gain insights into the underlying quantum behavior of the system. Furthermore, deviations from GOE predictions can signal the presence of external perturbations or the breakdown of this fundamental symmetry, offering a sensitive probe of the system’s environment and dynamics.

Recent investigations into quantum billiards – confined quantum systems where particles bounce around – reveal a surprising sensitivity in their energy spectra to even subtle interactions between order and chaos. Researchers have meticulously compared detailed simulations, executed using advanced software, with experimental observations, and both were rigorously assessed against predictions derived from Random Matrix Theory (RMT) and the Berry-Tabor Conjecture. This comparative analysis demonstrates that even weak coupling between regions exhibiting purely integrable (ordered) and chaotic behavior measurably alters the distribution of energy levels within the billiard. Specifically, deviations from the expected RMT behavior – traditionally associated with fully chaotic systems – become apparent, providing compelling evidence for a nuanced transition between quantum order and chaos and validating the theoretical framework used to describe these complex systems. The findings suggest that the interplay between these opposing behaviors is far more delicate than previously understood, with even minimal perturbations capable of leaving a discernible fingerprint on the system’s spectral properties.

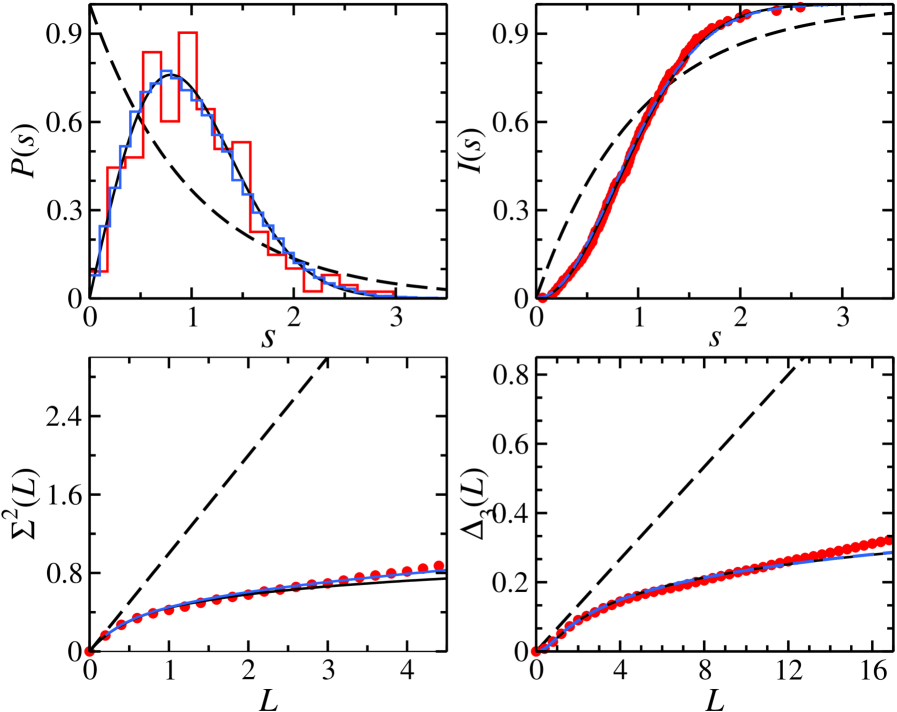
Removing the separating wall reveals a unified spectral response for the membrane <span class="katex-eq" data-katex-display="false">\lambda=3.5</span>, closely matching the predictions of the RMT model (blue) as compared to the separated response (red). — Removing the separating wall reveals a unified spectral response for the membrane $\lambda=3.5$ , closely matching the predictions of the RMT model (blue) as compared to the separated response (red).

Beyond the Semicircle: Charting Future Directions in Quantum Chaos

The Rosenzweig-Porter model represents a significant advancement in the study of quantum chaos by moving beyond simplistic, fully chaotic or fully regular systems. This model introduces a crucial element – the coexistence of both regular and chaotic dynamics within a single quantum system, achieved through a carefully tuned random matrix ensemble. Unlike earlier approaches, it doesn’t treat chaos as an all-or-nothing phenomenon; instead, it allows for a spectrum of behaviors, characterized by a mixing parameter that controls the relative strength of regular and chaotic components. This nuanced approach enables researchers to investigate how the interplay between these dynamics affects key quantum properties, such as energy level statistics and the localization of wavefunctions. Consequently, the Rosenzweig-Porter model offers a more realistic and comprehensive framework for analyzing complex quantum systems encountered in diverse physical scenarios, from heavy nuclei to disordered materials, and ultimately broadens the scope of investigations into the fundamental nature of quantum chaos.

A nuanced understanding of quantum chaos necessitates moving beyond simplistic models and incorporating the influence of symmetry. Investigations utilizing the Gaussian Symplectic Ensemble (GSE) – a probabilistic framework describing the statistical properties of quantum systems possessing time-reversal symmetry – reveal that symmetry profoundly alters the characteristics of chaotic behavior. Unlike systems described by the Gaussian Unitary Ensemble, which lacks time-reversal symmetry, the GSE predicts distinct spectral correlations and level repulsion patterns in the energy spectrum of chaotic systems. These subtle differences are not merely mathematical curiosities; they directly impact the dynamics of quantum systems and their sensitivity to initial conditions. Consequently, employing the GSE and similar symmetry-respecting ensembles provides a more accurate and complete picture of quantum chaos, enabling researchers to better model and predict the behavior of complex quantum systems in areas ranging from nuclear physics to the development of robust quantum technologies.

The theoretical advances in understanding quantum chaos, particularly through models like the Rosenzweig-Porter framework, extend far beyond purely academic interest. In nuclear physics, these insights aid in describing the complex energy levels and decay patterns of heavy nuclei, offering a pathway to more accurate modeling of nuclear reactions and stability. Simultaneously, the principles of quantum chaos are proving instrumental in the burgeoning field of quantum information processing. The sensitivity to initial conditions and the intricate dynamics inherent in chaotic systems can be harnessed to design robust quantum algorithms and explore novel approaches to quantum cryptography. Furthermore, the study of these systems offers potential for developing more efficient quantum random number generators, crucial for secure communication and simulations. This interdisciplinary convergence suggests that a deeper understanding of quantum chaos will not only refine fundamental physics but also catalyze the development of transformative technologies in diverse areas of science and engineering.

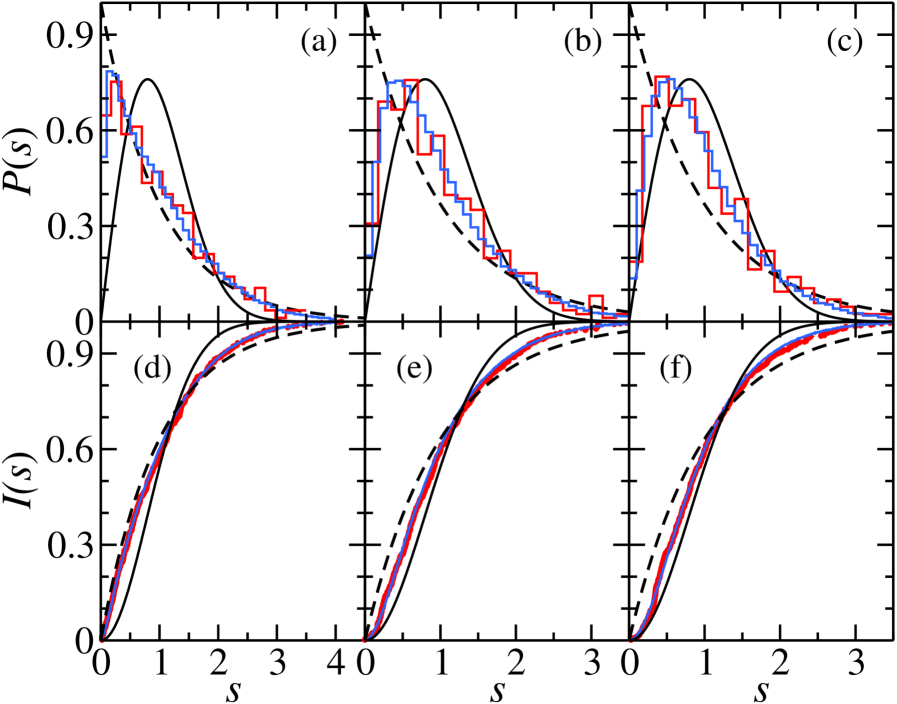
The distribution of nearest-neighbor spacing, <span class="katex-eq" data-katex-display="false">P(s)</span> and its cumulative form, <span class="katex-eq" data-katex-display="false">I(s)</span>, reveals a transition from Poisson statistics for weak coupling to Gaussian Orthogonal Ensemble (GOE) behavior for strong coupling (λ = 0.03, 0.23, and 0.35), as demonstrated by the agreement between experimental data (red) and Random Matrix Theory predictions (blue). — The distribution of nearest-neighbor spacing, $P(s)$ and its cumulative form, $I(s)$ , reveals a transition from Poisson statistics for weak coupling to Gaussian Orthogonal Ensemble (GOE) behavior for strong coupling (λ = 0.03, 0.23, and 0.35), as demonstrated by the agreement between experimental data (red) and Random Matrix Theory predictions (blue).

The research meticulously details how even subtle interactions between quantum billiards-systems exhibiting both integrable and chaotic dynamics-produce measurable shifts in spectral properties. This sensitivity to initial conditions and interconnectedness echoes a timeless principle. As Confucius stated, “Study the past if you would define the future.” The study’s findings, particularly regarding the influence of coupling strength on eigenvalue distributions, demonstrate that understanding the foundational ‘past’ – in this case, the individual billiard’s characteristics – is crucial for accurately predicting the system’s ‘future’ spectral behavior. The rigorous mathematical modeling employed aligns with the pursuit of demonstrable truth, a principle valued across disciplines.

Beyond the Billiard: Future Directions

The demonstration that even attenuated coupling fundamentally alters the spectral characteristics of otherwise well-defined quantum systems is, predictably, not a surprise. Rigor demands that interactions, however subtle, propagate through the Hilbert space, modifying eigenvalue distributions. The current work confirms this, albeit empirically. The true challenge lies not in observing these changes, but in formulating a predictive framework beyond the necessarily approximate Rosenzweig-Porter model. The elegance of Random Matrix Theory resides in its statistical nature; forcing it to describe specific, weakly-coupled systems introduces an inherent, and troubling, lack of mathematical purity.

Future investigations must address the limitations of current modeling techniques. Simply refining parameters within existing random matrix frameworks feels…unsatisfying. A more fundamental approach-one that derives spectral properties from first principles, acknowledging the underlying deterministic chaos-is necessary. The pursuit of a truly provable connection between classical dynamics and quantum spectral statistics remains a distant, yet compelling, goal.

Ultimately, the value of these experimental studies resides not in mimicking complexity, but in illuminating the boundaries of predictability. The system, after all, is not attempting to deceive; it simply is. The task for theorists is to reflect that inherent consistency – or to explain why attempts to do so consistently fail.

Original article: https://arxiv.org/pdf/2601.11212.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/