Author: Denis Avetisyan
New analysis reveals that long-baseline neutrino experiments offer a unique way to probe the foundations of quantum mechanics and demonstrate non-classical behavior.
Research shows that experiments like T2K can effectively test the Leggett-Garg inequality, revealing significant deviations from classical predictions in neutrino oscillations.
The foundations of classical physics struggle to fully describe phenomena at the quantum level, prompting ongoing tests of its limits. In the work ‘Exploring Quantumness at Long-Baseline Neutrino Experiments’, we investigate the potential for long-baseline neutrino experiments-MINOS, T2K, NOvA, and the future DUNE-to reveal deviations from classical behavior via violations of Leggett-Garg inequalities. Our data-driven analysis demonstrates statistically significant evidence for quantumness in neutrino oscillations, with T2K exhibiting a 14\sigma violation and projections for DUNE and NOvA also exceeding the 5\sigma threshold. Could these experiments ultimately provide a novel platform for probing the boundary between the quantum and classical worlds?
The Ghostly Puzzle: Neutrinos and the Limits of Knowing
Neutrinos, often called “ghost particles” due to their weak interactions with matter, present a profound puzzle for physicists: they spontaneously change “flavor” – oscillating between three distinct types: electron, muon, and tau. This isn’t a decay process, but a quantum mechanical phenomenon where a neutrino created as one flavor can be detected as another, sometimes even multiple times within the same experiment. The very existence of neutrino oscillation implies that neutrinos possess mass – a property not predicted by the Standard Model of particle physics, which originally posited them as massless. Consequently, understanding this oscillation is crucial not only for completing the Standard Model but also for potentially revealing physics beyond it, offering clues about the asymmetry between matter and antimatter in the universe and the nature of dark matter. The implications of this seemingly subtle behavior resonate deeply within the foundations of modern physics, pushing the boundaries of what is known about the fundamental constituents of reality.
Detecting neutrino oscillations-the spontaneous transformation of one neutrino “flavor” into another-demands experiments spanning vast distances, known as long-baseline setups. These experiments, like sending a faint signal across a noisy channel, face significant hurdles in discerning genuine oscillation patterns from background noise and systematic errors. The challenge lies in the inherent uncertainties associated with neutrino interactions and detector capabilities; these uncertainties aren’t merely statistical fluctuations, but fundamental limitations in precisely knowing the initial state of the neutrinos and how they behave within the detector. Sophisticated analysis techniques and precise calibration are therefore crucial, yet even with these efforts, teasing out the subtle signatures of oscillation requires careful consideration of these pervasive uncertainties, influencing the interpretation of results and the search for new physics.
The analysis of neutrino data has historically depended on approximations of experimental uncertainties, a practice that introduces potential systematic errors into the results. These simplifications, while computationally convenient, often fail to fully capture the complex interplay of factors influencing neutrino detection – including imperfect knowledge of detector response, backgrounds from other particles, and the intricacies of neutrino interactions. Consequently, established methods may inadvertently skew interpretations of neutrino oscillation parameters, leading to biased measurements of fundamental properties like neutrino masses and mixing angles. Researchers are now actively developing more sophisticated statistical techniques and data analysis frameworks to address these limitations, aiming to provide a more accurate and unbiased picture of these elusive particles and the physics governing their behavior.
Taming Uncertainty: A New Approach to Neutrino Analysis
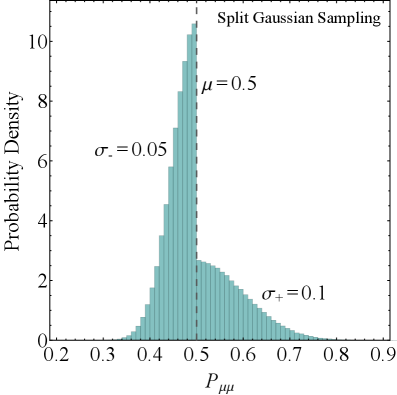
Neutrino data analysis frequently encounters uncertainties that deviate from the standard symmetrical, or Gaussian, distribution. This asymmetry arises because the probability of a measured value being higher or lower than the expected value is not equal; for example, systematic errors or limitations in detector response can disproportionately influence values in one direction. Traditional statistical methods, predicated on symmetrical uncertainties, can therefore produce inaccurate results when applied to neutrino data. Consequently, analytical techniques must explicitly model and account for these asymmetric uncertainties to provide reliable parameter estimation and hypothesis testing; failing to do so introduces bias and underestimates the true range of possible values.
Split-Gaussian Sampling is a Monte Carlo method employed to generate representative datasets from probability distributions exhibiting asymmetric uncertainties. Unlike traditional Monte Carlo techniques that assume symmetrical distributions, Split-Gaussian Sampling models asymmetric probability density functions as a sum of Gaussian distributions. Each Gaussian component is defined by a mean and standard deviation, and the sampling process draws values from these components with weights proportional to their contribution to the overall distribution. This approach allows for a more accurate representation of the uncertainty range, particularly when the probability of values deviating in one direction is significantly different than in another, which is common in neutrino physics data analysis. The technique effectively addresses the limitations of standard sampling methods when dealing with non-symmetrical error estimations.
The estimation of the Empirical Cumulative Distribution Function (ECDF) is a critical component of Split-Gaussian Sampling because it provides a non-parametric representation of the underlying probability distribution of the neutrino data. The ECDF, defined as the proportion of observations less than or equal to a given value, allows for a complete characterization of the data without assuming a specific functional form. By accurately constructing the ECDF, the sampling process can effectively represent the full range of possible values, particularly in the presence of asymmetric uncertainties, and mitigate biases that might arise from relying on simplified parametric models or incomplete data representation. This ensures a more robust and reliable statistical inference when analyzing complex neutrino interactions.
Beyond Classicality: Probing the Quantum Nature of Neutrinos
Current neutrino research extends beyond the established measurement of oscillation parameters – frequency and amplitude of neutrino transformations – to investigate potential non-classical correlations within neutrino behavior. This investigation aims to determine if neutrinos exhibit properties inconsistent with classical physics, which assumes definite properties independent of measurement. Specifically, researchers are examining whether correlations between neutrino properties at different times violate the bounds predicted by classical realism, a worldview where systems possess pre-defined states. The motivation for this research stems from the potential for neutrinos to exhibit uniquely quantum behavior, potentially challenging fundamental assumptions about the nature of reality and prompting re-evaluation of existing physical models.
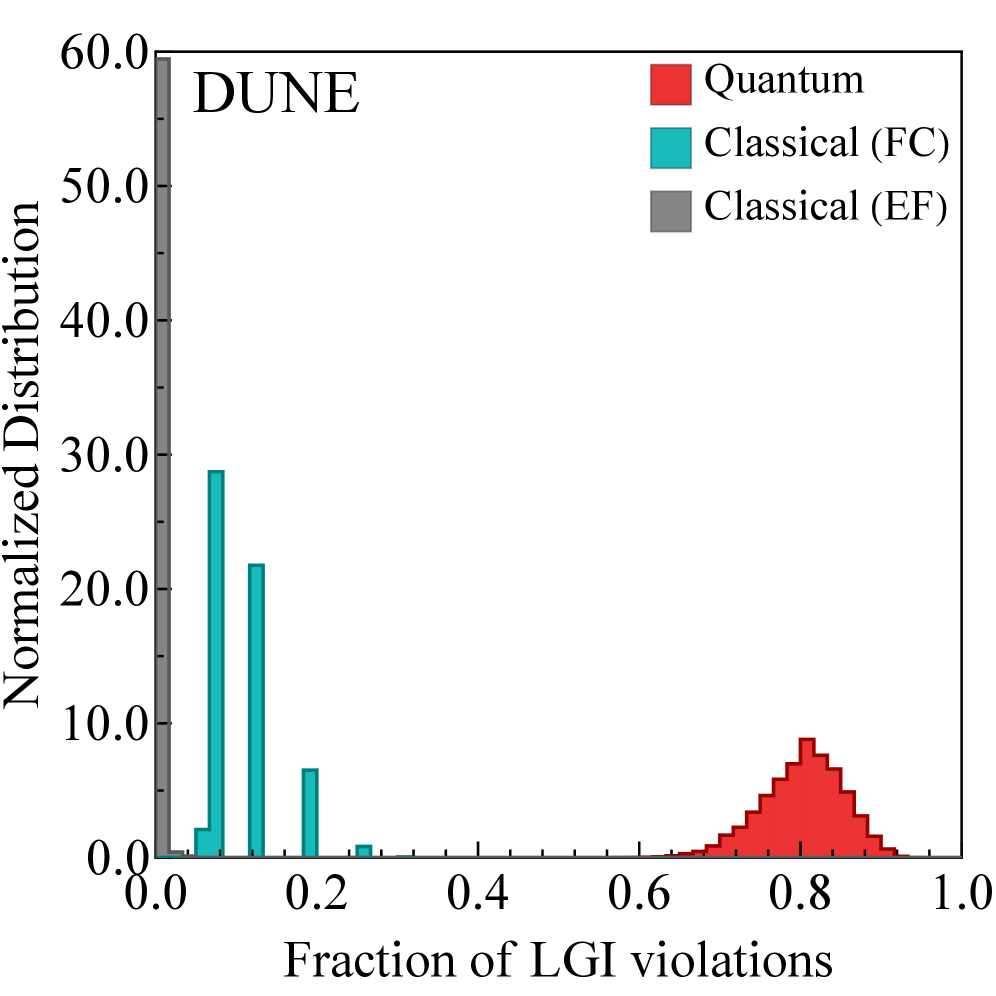
The Leggett-Garg Inequality (LGI) is a temporal Bell inequality designed to detect non-classical correlations in time-dependent quantum systems. Unlike spatial Bell inequalities which examine correlations between spatially separated measurements, the LGI focuses on correlations between measurements performed on a single system at different points in time. The inequality establishes a limit on the correlation strength achievable by any locally realistic theory – a theory assuming properties are pre-determined and influenced only by their immediate surroundings. Mathematically, for a system measured at times t_i, the LGI typically takes the form S = \sum_{i,j} E(t_i, t_j) \leq 2, where E(t_i, t_j) represents the correlation function between measurements at times t_i and t_j. Violation of this inequality – obtaining a value S > 2 – indicates that the system exhibits correlations incompatible with local realism, thus demonstrating non-classical behavior. The LGI provides a quantifiable benchmark against which experimental results can be compared to assess the degree of quantumness in a system’s dynamics.
Analysis of data from the NOvA, T2K, and MINOS experiments utilizes the Leggett-Garg inequality in conjunction with the Root Mean Square z-score (RMS z-score) to assess deviations from classical predictions regarding neutrino oscillation. These analyses have demonstrated statistically significant violations of classical realism, indicating non-classical correlations in neutrino behavior. The T2K experiment currently provides the strongest evidence for these violations, reporting a statistical significance of 13.86 σ, which exceeds the standard threshold for discovery in particle physics.
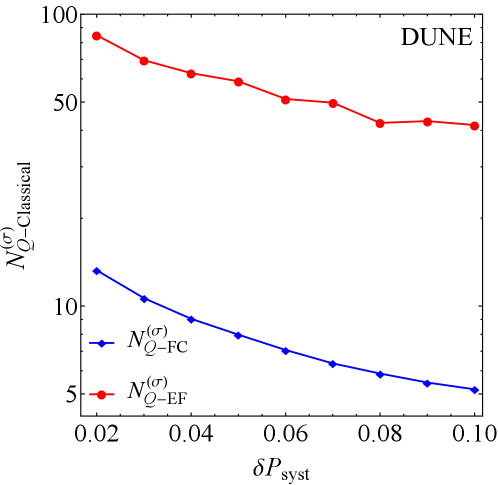
The Future is Quantum: Expanding the Boundaries of Neutrino Physics
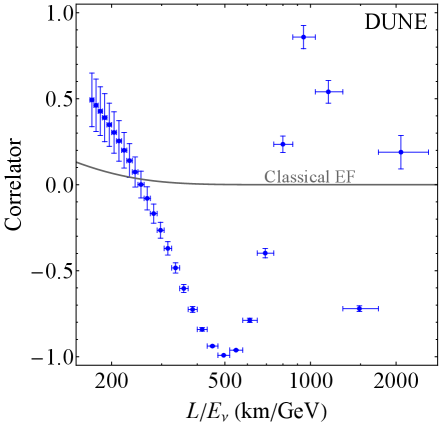
Attempts to describe neutrino behavior using purely classical models – specifically, approaches like the ‘Classical Factorized Correlator’ and ‘Classical Exponential Fit’ – consistently fail when subjected to rigorous testing via the Leggett-Garg Inequality. This inequality, originally developed for quantum mechanics, provides a benchmark for distinguishing between classical and non-classical correlations in time. Experiments reveal a clear violation of the Leggett-Garg Inequality when applied to neutrino oscillation data, indicating that these particles exhibit correlations that cannot be explained by classical physics. The observed behavior suggests that neutrinos are fundamentally quantum mechanical, displaying properties like superposition and entanglement in their temporal evolution, and challenging the notion that their behavior can be adequately described by deterministic, locally realistic models.
The Deep Underground Neutrino Experiment, or DUNE, currently under construction, represents a pivotal leap forward in the pursuit of understanding these elusive particles and the quantum principles governing their behavior. This ambitious project is designed to amass an unprecedented volume of neutrino data with a projected statistical significance of 7.98 σ – a level of certainty that far surpasses current experiments. Such precision will enable researchers to rigorously test the boundaries of classical physics as applied to neutrinos, specifically through assessments against inequalities like the Leggett-Garg Inequality, which probes for non-classical correlations. Ultimately, DUNE isn’t simply about detecting neutrinos; it’s about pushing the limits of what can be known about the quantum world and revealing whether these particles adhere to, or defy, our established understanding of reality.
The pursuit of increasingly precise measurements and sophisticated statistical methods is currently driving neutrino physics toward a deeper understanding of fundamental quantum principles. Researchers are not simply seeking to confirm existing models, but rather to expose potential deviations from classical behavior, pushing the limits of what is known about these elusive particles. This dedication to enhanced precision, exemplified by projects like DUNE, allows for increasingly stringent tests of quantum mechanics itself, potentially revealing subtle connections between neutrino properties and the broader quantum world. The expectation is that continued advancements in both experimental capabilities and analytical techniques will ultimately unlock previously inaccessible insights into the very fabric of reality, extending beyond the realm of particle physics and into the foundations of quantum theory.
The pursuit of quantumness within long-baseline neutrino experiments, as detailed in the study, echoes a humbling truth about the limits of observation. Each Monte Carlo simulation, each attempt to statistically analyze neutrino oscillations and test the Leggett-Garg Inequality, is a grasping at shadows. As Friedrich Nietzsche observed, “There are no facts, only interpretations.” The data, meticulously gathered and processed, doesn’t reveal an absolute reality, but rather a construction built upon assumptions and approximations. The experiment doesn’t prove quantum mechanics, it demonstrates its consistency within the bounds of current measurement – a fleeting glimpse beyond the event horizon of what is knowable.
What Lies Beyond the Horizon?
The pursuit of quantumness in long-baseline neutrino experiments, as detailed in this work, is not a validation of a theory, but a mapping of its boundaries. Any demonstration of non-classicality is, inherently, a temporary one. The universe does not concern itself with human definitions of ‘classical’ or ‘quantum’; it simply is. The sensitivity achieved with T2K, and the potential for future facilities, merely pushes the event horizon of that ignorance a little further away. It’s a useful exercise, certainly, but one should not mistake the map for the territory.
The statistical challenges remain substantial. The RMS z-score, while a robust indicator, is still susceptible to the limitations of Monte Carlo simulations and the inherent noise of real-world data. Future investigations must focus not only on increasing statistical power but also on developing more sophisticated methods for disentangling genuine quantum effects from systematic uncertainties. The goal is not to prove quantum mechanics-that is, ultimately, a self-fulfilling prophecy-but to identify where its predictions begin to fail.
Black holes are perfect teachers; they show the limits of knowledge. The very act of observation, of attempting to define the quantum realm, inevitably alters it. This research, and those that follow, will continue to refine the questions, not necessarily the answers. Any theory is good, until light leaves its boundaries. The true horizon lies not in the data, but in the acceptance that some things will always remain unseen.
Original article: https://arxiv.org/pdf/2601.15375.pdf
Contact the author: https://www.linkedin.com/in/avetisyan/
See also:
- Best Controller Settings for ARC Raiders
- Donkey Kong Country Returns HD version 1.1.0 update now available, adds Dixie Kong and Switch 2 enhancements
- How To Watch A Knight Of The Seven Kingdoms Online And Stream The Game Of Thrones Spinoff From Anywhere
- Hytale: Upgrade All Workbenches to Max Level, Materials Guide
- Darkwood Trunk Location in Hytale
- Ashes of Creation Rogue Guide for Beginners
- PS5’s Biggest Game Has Not Released Yet, PlayStation Boss Teases
- When to Expect One Piece Chapter 1172 Spoilers & Manga Leaks
- Nicole Richie Reveals Her Daughter, 18, Now Goes By Different Name
- Olympian Katie Ledecky Details Her Gold Medal-Winning Training Regimen
2026-01-23 08:34