Mapping the Edge of Matter: Where Quarks Break Free

by

Author: Denis Avetisyan

A new study combines established models to pinpoint the critical endpoint in the QCD phase diagram, revealing the interplay between chiral symmetry breaking and the deconfinement transition.

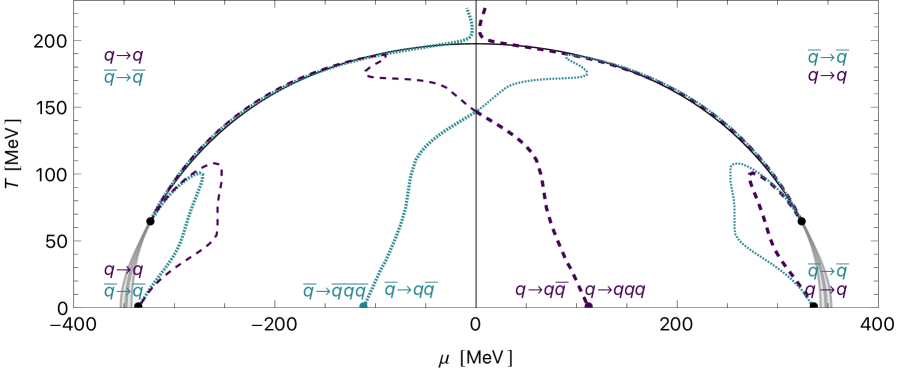
The phase diagram delineates a landscape of quark behavior, where inflections in net quark number gains-measured for both quarks and antiquarks-reveal a chiral crossover and potential divergences at the critical endpoint, signifying transitions between states of differing quark density (<span class="katex-eq" data-katex-display="false">0</span> to <span class="katex-eq" data-katex-display="false">±3</span> or <span class="katex-eq" data-katex-display="false">±3</span> to <span class="katex-eq" data-katex-display="false">±1</span>) as a probe is absorbed into the medium.
The phase diagram delineates a landscape of quark behavior, where inflections in net quark number gains-measured for both quarks and antiquarks-reveal a chiral crossover and potential divergences at the critical endpoint, signifying transitions between states of differing quark density (0 to ±3 or ±3 to ±1) as a probe is absorbed into the medium.

Researchers utilize a combined Nambu-Jona-Lasinio and Curci-Ferrari approach to explore the behavior of net quark number density and thermodynamic quantities near the critical endpoint.

Understanding the intricate relationship between chiral symmetry breaking and deconfinement remains a central challenge in quantum chromodynamics (QCD). This work, ‘Interplay between the chiral and deconfinement transitions from a Curci-Ferrari-based Polyakov loop potential’, investigates this interplay through a combined model leveraging the Nambu-Jona-Lasinio (NJL) model coupled to a gluonic background derived from a Curci-Ferrari approach to the Polyakov loop. The resulting phase diagram reveals a critical endpoint and characterizes thermodynamic observables, highlighting the utility of net quark number density as a probe of QCD phases. Could this framework offer a more robust understanding of the complex regions of the phase diagram where conventional Polyakov loop analyses may prove ambiguous?

The Echo of Creation: Exploring the Quark-Gluon Puzzle

Quantum Chromodynamics, the established theory of the strong force, posits that at extremely high temperatures or densities, matter undergoes a dramatic transformation. Normally, quarks and gluons – the fundamental constituents of protons and neutrons – are permanently confined within hadrons. However, QCD predicts a state where these particles become deconfined, existing as a plasma of quarks and gluons. Pinpointing the precise conditions and characteristics of this transition remains a substantial challenge for physicists. This isn’t simply an academic exercise; understanding this phase change is crucial for modeling the conditions that existed moments after the Big Bang and for accurately describing the internal structure of incredibly dense objects like neutron stars. The complexity arises from the sheer strength of the strong force, which makes traditional calculation methods ineffective, demanding innovative theoretical approaches and intensive computational modeling to map out this fundamental state of matter.

The study of the quark-gluon plasma-a state of matter theorized to have existed shortly after the Big Bang-is hampered by the limitations of conventional calculation techniques. At the extreme temperatures and densities where quarks and gluons are no longer confined within hadrons, the strong nuclear force-described by Quantum Chromodynamics (QCD)-becomes incredibly potent. This intensity renders traditional perturbative methods, which rely on approximating solutions with small corrections, utterly ineffective. These methods break down because the interactions are too strong to be treated as minor disturbances. Consequently, physicists must employ non-perturbative approaches, such as lattice QCD-a computationally intensive method that discretizes spacetime-to model the behavior of quarks and gluons and map the phase diagram of this exotic state of matter. These techniques, while complex, offer the only viable pathway to understanding the transition from confined hadronic matter to the deconfined quark-gluon plasma and its implications for both the early universe and the interiors of neutron stars.

The precise character of the quark-gluon plasma transition-whether a smooth crossover or a sharp, first-order phase transition-profoundly impacts understandings of both the primordial universe and the interiors of neutron stars. A first-order transition would have involved the nucleation and expansion of bubbles of deconfined plasma in the early universe, potentially leaving observable signatures in gravitational waves or affecting primordial element abundances. Conversely, a smooth crossover, currently favored by lattice QCD calculations, suggests a more gradual shift in matter’s properties. Within neutron stars, the equation of state-dictating the relationship between pressure and density-is critically sensitive to this transition; a first-order transition could lead to dramatic instabilities or even the formation of exotic matter, while a crossover would result in a more conventional, albeit still extreme, stellar structure. Determining the true nature of this transition, therefore, remains a pivotal challenge with far-reaching consequences for astrophysics and cosmology.

The temperature dependence of order parameters at a chemical potential of <span class="katex-eq" data-katex-display="false"> \mu=M_{0} \sim eq 336 </span> MeV reveals a first-order transition (filled points) occurring as the system traverses the spinodal region, evidenced by inflection points (open points) and the presence of metastable/unstable extrema (thin lines).
The temperature dependence of order parameters at a chemical potential of \mu=M_{0} \sim eq 336 MeV reveals a first-order transition (filled points) occurring as the system traverses the spinodal region, evidenced by inflection points (open points) and the presence of metastable/unstable extrema (thin lines).

Breaking Symmetry: A Model for the Primordial Soup

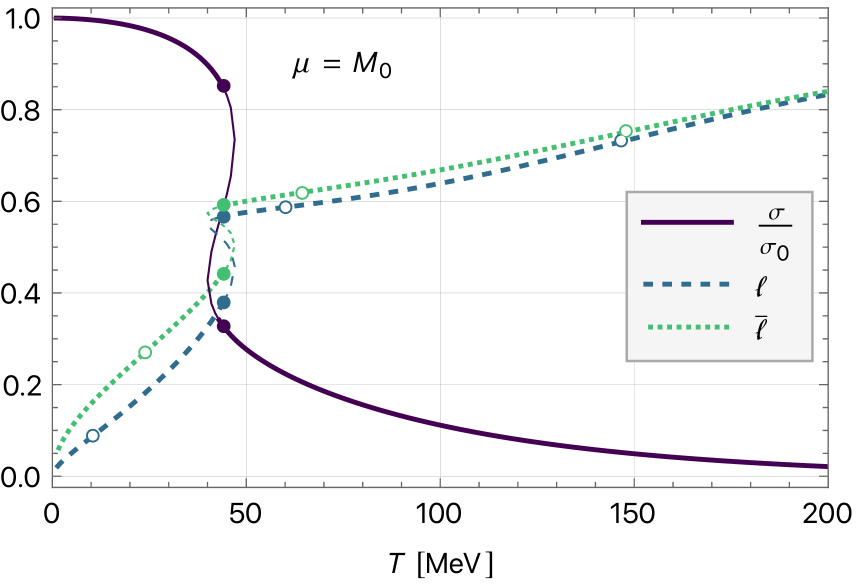
The Nambu-Jona-Lasinio (NJL) model is a four-fermion interaction model used in particle physics to describe the dynamics of quarks and explain the phenomenon of spontaneous chiral symmetry breaking. In the limit of massless quarks, the Lagrangian is chirally symmetric, but this symmetry is spontaneously broken due to the formation of a quark condensate \langle \overline{q}q \rangle in the vacuum state. This condensate effectively gives quarks a dynamical mass, even though they are initially massless in the model. The model’s key feature is its non-perturbative nature, allowing it to address strong interaction physics where perturbative methods fail. While the NJL model effectively describes the breaking of chiral symmetry, it does not inherently provide a mechanism for confinement – the observation that quarks are never found in isolation – and is therefore often extended with other concepts, such as the Polyakov Loop, to address this aspect of quantum chromodynamics.

The Nambu-Jona-Lasinio (NJL) model, while effective in describing spontaneous chiral symmetry breaking through the formation of a dynamical mass for quarks, inherently lacks a mechanism to represent confinement and deconfinement. This is because the NJL model treats quarks as fundamental degrees of freedom without explicitly accounting for color interactions responsible for confining quarks within hadrons. The Polyakov Loop, a loop integral of the color-averaged quark propagator, serves as an order parameter for the confinement/deconfinement transition in Quantum Chromodynamics (QCD). By incorporating the Polyakov Loop into the NJL model, forming the PNJL model, a dynamical variable is introduced that reflects the change in the free energy associated with spatial quark loops, effectively signaling the transition between confined and deconfined phases of quark matter.

The Polyakov-Nambu-Jona-Lasinio (PNJL) model extends the NJL model by incorporating the Polyakov Loop, a complex-valued field \varPhi, to explicitly represent confinement and deconfinement dynamics. The Polyakov Loop acts as a dynamical order parameter for the transition between the confined and deconfined phases of Quantum Chromodynamics (QCD). This integration allows for a simultaneous investigation of both the chiral phase transition, already addressed by the NJL model through spontaneous chiral symmetry breaking, and the confinement/deconfinement crossover. Specifically, the PNJL model introduces terms into the NJL Lagrangian involving the Polyakov Loop and its conjugate, modifying the effective potential and influencing the behavior of the fermion propagator, ultimately enabling the study of the interplay between chiral restoration and deconfinement at finite temperature and density.

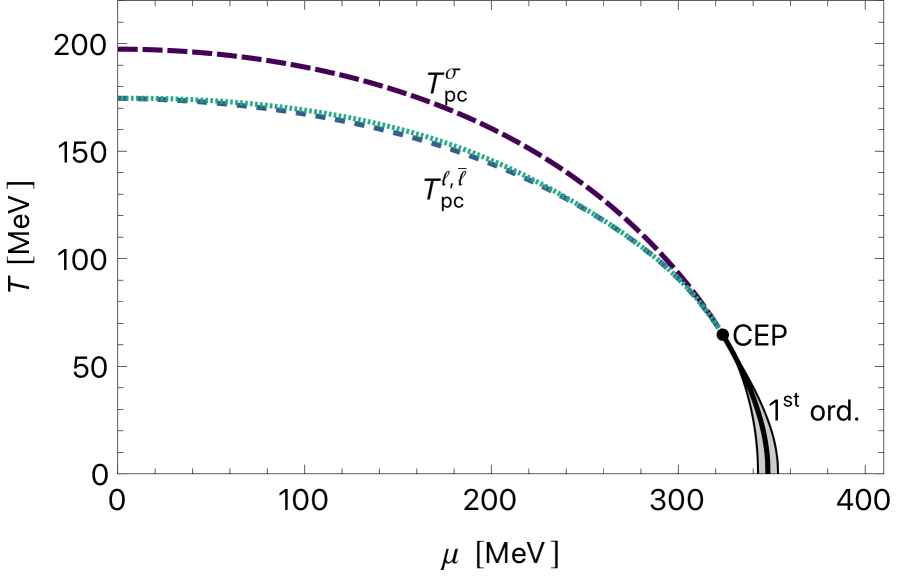
The phase diagram of the csCF-PNJL model, depicted in the <span class="katex-eq" data-katex-display="false">\(\\mu, T\\)</span>-plane, reveals crossovers of the <span class="katex-eq" data-katex-display="false">\(\\sigma, \\ell, \\bar{\\ell}\\)</span> order parameters (lighter, dotted lines), a critical endpoint (black dot), and a spinodal region/first-order transition line consistent across all three parameters, as detailed in Appendix B.
The phase diagram of the csCF-PNJL model, depicted in the \(\\mu, T\\)-plane, reveals crossovers of the \(\\sigma, \\ell, \\bar{\\ell}\\) order parameters (lighter, dotted lines), a critical endpoint (black dot), and a spinodal region/first-order transition line consistent across all three parameters, as detailed in Appendix B.

Refining the Mirror: Injecting Gauge Dynamics

The PNJL (Polyakov-Nambu-Jona-Lasinio) model, while effective in describing quark-gluon plasma dynamics, requires refinement through the inclusion of gauge dynamics to enhance its accuracy and realism. Standard PNJL formulations often simplify the interactions between quarks and gluons, neglecting crucial non-perturbative effects arising from the gauge field. Incorporating these effects, which govern the strong force and confinement of quarks, is critical for a more complete and physically relevant description of the quark-gluon plasma and its phase transitions. Addressing these limitations allows for improved predictions regarding deconfinement temperature and the equation of state of strongly interacting matter, ultimately bridging the gap between theoretical models and experimental observations from heavy-ion collision experiments.

The Curci-Ferrari model addresses confinement in non-Abelian gauge theories by introducing a dynamically generated gluon mass. This is achieved through a representation of the gluon propagator that includes a scalar field coupled to the field strength tensor, effectively modifying the infrared behavior of gluons and suppressing the long-range interactions responsible for color screening. The model provides a systematic, perturbative expansion around a background gauge field, allowing for the calculation of non-perturbative effects related to confinement without relying on lattice QCD simulations. Specifically, the inclusion of the Curci-Ferrari terms alters the functional form of the gluon propagator, introducing a pole at a finite momentum, which corresponds to a massive gluon, and thereby contributes to the effective potential governing confinement and deconfinement transitions.

Integration of the Curci-Ferrari model with the Polyakov-Nambu-Jona-Lasinio (PNJL) framework seeks to improve the modeling of quark confinement and the deconfinement transition. This approach allows for a more accurate description of non-perturbative quantum chromodynamics (QCD) effects, particularly those related to gluon dynamics. Analysis within this combined framework has identified a critical endpoint at approximately (324 MeV, 64 MeV), determined by locating inflection points in relevant order parameters characterizing the phase transition. This point signifies the conditions under which the transition between confined and deconfined quark-gluon plasma is predicted to occur, providing quantitative predictions for experiments in heavy-ion collisions.

Varying the renormalization scale ξ reveals that the center-of-energy point shifts predictably for both pure Yang-Mills (circles) and QCD-fit (squares) parameter sets, with the <span class="katex-eq" data-katex-display="false">\xi = 0</span> limit indicated by filled symbols.
Varying the renormalization scale ξ reveals that the center-of-energy point shifts predictably for both pure Yang-Mills (circles) and QCD-fit (squares) parameter sets, with the \xi = 0 limit indicated by filled symbols.

The Limits of Knowledge: Confronting the Sign Problem

A fundamental challenge in exploring the behavior of matter under extreme conditions, such as those found in neutron stars and heavy-ion collisions, lies in the ‘Sign Problem’ inherent to lattice Quantum Chromodynamics (QCD). This problem arises when simulating systems at finite chemical potential – a measure of the baryon density – causing the mathematical determinants used in the lattice QCD calculations to become complex and oscillatory. Consequently, standard Monte Carlo methods, which rely on averaging over many configurations, become ineffective, yielding results with exceedingly high statistical noise or failing to converge altogether. The severity of the Sign Problem increases with chemical potential, effectively limiting the range of densities that can be reliably accessed and hindering a complete understanding of the quark-gluon plasma’s properties in environments with significant baryon density, crucial for modeling astrophysical objects and the early universe.

Determining the equation of state for the quark-gluon plasma presents a significant challenge in high-energy physics, as it dictates the fundamental relationship between pressure, temperature, and energy density within this exotic state of matter. Accurate calculation of this equation of state is vital for interpreting experimental results from heavy-ion collisions and for modeling the behavior of neutron stars, yet it is severely hindered by the ‘Sign Problem’ inherent in lattice quantum chromodynamics (QCD) calculations. This problem arises from the oscillatory nature of the determinant in the path integral, leading to exponentially increasing statistical errors that prevent reliable simulations at finite chemical potential-conditions relevant to many astrophysical scenarios. Consequently, researchers often rely on approximations and alternative models, such as the PNJL model, to gain insights, acknowledging that a complete and precise equation of state remains a key goal for future theoretical and computational advancements.

The Polyakov-Nambu-Jona-Lasinio (PNJL) model provides valuable, though preliminary, insights into the quark-gluon plasma, serving as a crucial foundation for more complex investigations. Recent analysis using this model identifies a pseudo-critical temperature of approximately 175 MeV, determined by examining the inflection point in the temperature susceptibility of relevant order parameters. While calculations of n_q/T^3 show a roughly 15% deviation when compared to Nf=2 lattice data at T=2T_{pc} , the model successfully predicts the behavior of the quark-gluon plasma at higher temperatures. Specifically, the calculated speed of sound ( c_s^2 ) approaches the theoretical value of 1/3, aligning with results from continuum extrapolated Nf=2+1 lattice data, and the trace anomaly ( \epsilon - 3p )/ T^4 is qualitatively reproduced, demonstrating the PNJL model’s capacity to capture key thermodynamic properties of this exotic state of matter.

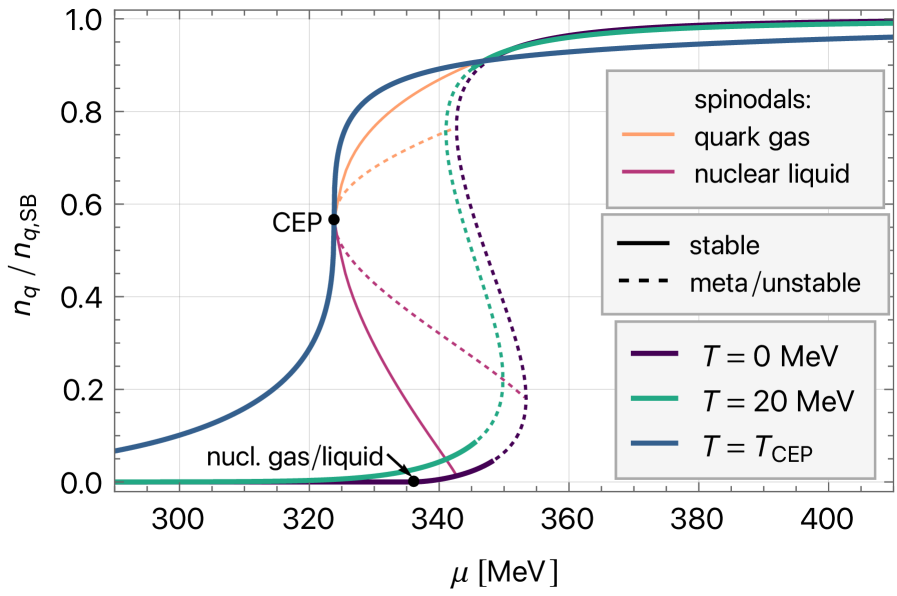
Normalized quark number density exhibits distinct behaviors at different temperatures within the spinodal region, revealing the densities of chirally broken (magenta) and restored (orange) phases emanating from the critical endpoint and defining the boundaries of the phase coexistence region.
Normalized quark number density exhibits distinct behaviors at different temperatures within the spinodal region, revealing the densities of chirally broken (magenta) and restored (orange) phases emanating from the critical endpoint and defining the boundaries of the phase coexistence region.

The pursuit of a comprehensive QCD phase diagram, as detailed in this work combining the NJL and Curci-Ferrari models, reveals a humbling truth about theoretical frameworks. One is reminded of Niels Bohr’s observation: “The opposite of every truth is also a truth.” The search for the critical endpoint, a singular point defining the transition between chiral symmetry breaking and deconfinement, demonstrates this elegantly. Each model, however meticulously constructed, represents a limited perspective, a specific ‘light’ illuminating a portion of the landscape. Beyond the reach of current data, any seemingly perfect theoretical construct, much like light, may ultimately vanish – its validity constrained by the event horizon of empirical verification. The model’s success hinges on navigating the delicate interplay of net quark number density and temperature, a testament to the inherent complexity and provisional nature of all theoretical endeavors.

What Lies Beyond the Horizon?

The construction of any effective model, as demonstrated by this interplay between the Nambu-Jona-Lasinio and Curci-Ferrari frameworks, invariably rests on a negotiated surrender. A simplification, however elegant, always obscures a greater complexity, a wilderness of interactions left unmapped. The locating of a critical endpoint within the QCD phase diagram – a region of presumed exotic physics – feels less like a discovery and more like charting a particularly well-lit corner of an infinite darkness. Each measurement is a compromise between the desire to understand and the reality that refuses to be understood.

Future explorations will undoubtedly refine the potential describing the Polyakov loop, perhaps incorporating dynamical quarks or more sophisticated treatment of the infrared divergences. Yet, the fundamental question remains: is the true structure of quantum chromodynamics amenable to such approximations? Or are these models merely transient illusions, destined to dissolve beyond the event horizon of an ever-receding truth? The pursuit of chiral symmetry breaking and deconfinement is, in essence, a testing of the limits of human intuition.

One does not uncover the universe – one tries not to get lost in its darkness. The next iteration of this work – and countless others like it – will likely yield finer resolution, more precise predictions. But the most valuable outcome may not be a definitive answer, but a clearer recognition of the questions that remain, those swirling uncertainties that remind one of the inherent unknowability at the heart of it all.

Original article: https://arxiv.org/pdf/2601.15839.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/

See also:

2026-01-24 08:08