Black Hole Echoes: Nonlinearity’s Subtle Impact

Author: Denis Avetisyan

New research reveals that while massive scalar fields exhibit predictable behavior around black holes, quadratic quasinormal modes may offer a pathway to observe previously hidden nonlinear dynamics.

Nonlinear simulations demonstrate the temporal evolution of massive scalar perturbations, where rescaling the evolved field as <span class="katex-eq" data-katex-display="false">{\Phi\_{lm}}={\lambda^{n}}\phi\_{lm}^{(n)}</span> reveals that the <span class="katex-eq" data-katex-display="false">(0,0)</span> mode arises from the quadratic self-couplings of the linear <span class="katex-eq" data-katex-display="false">(1,1)</span>, <span class="katex-eq" data-katex-display="false">(0,0)</span>, and <span class="katex-eq" data-katex-display="false">(2,0)</span> modes, and exhibits excellent agreement between intermediate-time analytical predictions and corresponding numerical evolution. — Nonlinear simulations demonstrate the temporal evolution of massive scalar perturbations, where rescaling the evolved field as ${\Phi\_{lm}}={\lambda^{n}}\phi\_{lm}^{(n)}$ reveals that the $(0,0)$ mode arises from the quadratic self-couplings of the linear $(1,1)$ , $(0,0)$ , and $(2,0)$ modes, and exhibits excellent agreement between intermediate-time analytical predictions and corresponding numerical evolution.

This study investigates the influence of nonlinear effects on the intermediate-time tails of massive scalar perturbations in the spacetime around black holes.

While black hole ringdown is typically modeled using linear perturbation theory, nonlinear effects are crucial for a complete understanding of gravitational-wave observations. This research, entitled ‘Nonlinear tails of massive scalar fields around a black hole’, systematically investigates the nonlinear dynamics of massive scalar perturbations in the spacetime surrounding a black hole, contrasting them with linear predictions. We find that, surprisingly, the intermediate-time tails of these massive fields exhibit decay rates independent of source parameters, unlike their massless counterparts-suggesting minimal impact from nonlinearities in this regime. Could the subtle signatures of quadratic quasinormal modes ultimately serve as a more sensitive probe of the nonlinear dynamics governing black hole ringdown?

The Ringdown’s Echo: Probing Gravity’s Extremes

The final moments of a black hole merger, termed the ‘ringdown’, represent a unique opportunity to probe the very nature of gravity. As the newly formed black hole settles into a stable state, it emits gravitational waves that gradually diminish in amplitude – a process akin to striking a bell and listening to the fading resonance. These waves aren’t random; they encode information about the black hole’s mass and spin, but more profoundly, they offer a testing ground for Einstein’s theory of general relativity in its most extreme regime. Subtle deviations in the ringdown signal from theoretical predictions could reveal the presence of previously unknown physics, potentially hinting at modifications to general relativity or the existence of exotic objects beyond our current understanding. Precisely characterizing this late-time gravitational wave signature is therefore paramount, as it functions as a gravitational echo of the merger, resonating with fundamental questions about the universe.

The ringdown phase following a black hole merger is remarkably well-described by Linear Perturbation Theory, a cornerstone of gravitational physics. This established framework predicts that the newly formed black hole, momentarily disturbed by the collision, will settle into a stable state through a series of exponentially decaying oscillations. These oscillations, akin to the ringing of a bell after being struck, are characterized by specific frequencies and damping rates dictated by the black hole’s mass and spin. Crucially, the theory also anticipates a characteristic tail – known as the ‘Price Tail’ – extending beyond the dominant oscillations; this slowly fading signal represents the propagation of gravitational waves carrying away the excess energy and ultimately allowing the black hole to fully stabilize. While incredibly successful in modeling observed ringdown signals, the inherent assumptions within Linear Perturbation Theory-specifically, the consideration of only small disturbances-prompt ongoing investigation into potential refinements that may capture more nuanced, nonlinear effects.

Current models of black hole ringdown, built upon Linear Perturbation Theory, operate under the assumption that the disturbances created by a merger are relatively small-a simplification that allows for manageable calculations. Yet, the extreme gravity near a black hole suggests that these disturbances might, in reality, be far from negligible. These potentially significant nonlinear effects could subtly alter the predicted decay of the ringdown signal-shifting the frequencies of the emitted gravitational waves, modifying the characteristic $Price Tail$ , and even influencing the final mass and spin of the resulting black hole. Detecting these deviations from the linear predictions would not only refine understanding of gravity in its most extreme form, but also serve as a powerful test of Einstein’s theory, potentially revealing the need for more complex models that fully account for the interplay of spacetime distortions.

Numerical simulations of scalar field perturbations demonstrate that analytical predictions accurately model both linear and nonlinear evolution for massless fields and, surprisingly, also capture the behavior of massive fields during intermediate time scales.

Massive Fields: Modifying the Ringdown’s Signature

The ringdown phase following a black hole merger, characterized by the damped oscillation of the newly formed black hole, is demonstrably affected by the presence of a massive scalar field. A $\text{Massive Scalar Field}$ surrounding a $\text{Schwarzschild Black Hole}$ introduces perturbations that modify the characteristic frequencies and damping times of the quasi-normal modes. Specifically, the field’s mass directly influences these modifications; larger field masses result in more pronounced shifts in the ringdown signal’s spectrum. These mass-dependent alterations are quantifiable and, in principle, allow for the extraction of the scalar field’s mass by precisely measuring the frequencies and decay rates present in the gravitational wave signal. The deviations from the standard $\text{Schwarzschild Black Hole}$ ringdown are proportional to the field’s mass and coupling strength, providing a pathway to test beyond-Einsteinian theories.

The $\text{Price Tail}$ of a gravitational wave signal, representing late-time echoes following the main ringdown, is susceptible to modification by the presence of a massive scalar field surrounding a black hole. This field introduces additional decay rates to the tail, effectively altering its exponential decay. The specific change in decay rate is directly related to the mass of the scalar field; therefore, precise measurements of the $\text{Price Tail}$ ’s decay can, in principle, be used to infer the mass of the field. Deviations from the standard $e^{-t/\tau}$ decay expected from general relativity would signify the presence and characteristics of this field, providing a potential avenue for detection.

Superradiance, occurring around rotating black holes, represents an amplification mechanism for incident waves under specific conditions – notably when the wave frequency ω satisfies $\omega < m\Omega_H$ , where $m$ is the azimuthal mode number and $\Omega_H$ is the black hole’s angular velocity. This condition leads to an exponential growth of the wave’s amplitude, potentially forming a dense cloud of massive scalar fields surrounding the black hole. The presence of this cloud significantly alters the gravitational wave signal emitted during the ringdown phase following a black hole merger, complicating the standard analysis by introducing additional frequencies and damping rates. The cloud’s density is directly related to the scalar field’s mass and the black hole’s rotation rate, making the ringdown signal a potential probe of both parameters, but also requiring more complex models to accurately interpret the observed waveforms.

Quasinormal oscillations and decaying tails are observed in massive scalar perturbations, exhibiting both source-free and source-driven wave behavior with both outgoing and ingoing components.

Numerical Solutions: Evolving the Ringdown’s Dynamics

Double-Null Evolution is a numerical technique utilized to solve hyperbolic partial differential equations, specifically wave equations, by leveraging a coordinate system aligned with the null surfaces of the spacetime. This method is particularly suited for simulating the propagation of fields, such as the $Massive Scalar Field$ , in strong gravitational fields like those surrounding black holes. The technique discretizes the wave equation using a finite difference scheme on a carefully chosen grid that adapts to the light cones, effectively tracing the evolution of the field as signals propagate both inward and outward from the black hole horizon. This allows for accurate modeling of the field’s behavior without requiring explicit specification of initial data on a global spacelike hypersurface, which can be problematic in dynamical spacetimes.

The Finite Difference Method (FDM) is utilized to discretize the continuous partial differential equations governing the Massive Scalar Field, transforming them into a system of algebraic equations solvable by computational means. This discretization involves approximating derivatives with finite differences – specifically, evaluating the rate of change of the field at discrete points in space and time. By representing the field values on a grid, FDM allows for the replacement of differential operators with algebraic expressions involving neighboring grid points. This process enables efficient computation, reducing the complexity of solving the wave equation while maintaining acceptable accuracy, and is crucial for simulating the evolution of the field in the vicinity of the black hole.

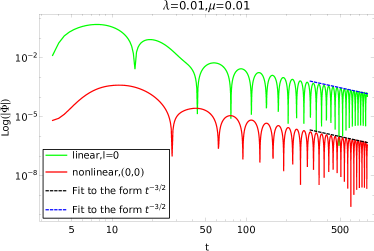
Simulations of the $\Massive Scalar Field$ evolution allow for direct comparison with predictions derived from Linear Perturbation Theory (LPT). LPT provides an analytical approximation of gravitational waves, but its validity diminishes in strong gravitational regimes or for fields with significant self-interaction. By numerically solving the governing equations without the simplifying assumptions of LPT, we can quantify deviations in the waveform, frequency, and damping time of the ringdown signal. Specifically, we analyze the emitted gravitational waves to identify nonlinear effects, such as the production of higher-order harmonics or modifications to the quasi-normal mode spectrum, that are not captured by the linear approximation. These deviations provide crucial insights into the validity range of LPT and inform the development of more accurate theoretical models.

Numerical evolution of massive scalar perturbations for linear and nonlinear modes demonstrates excellent agreement with linear analytical predictions for intermediate-time tails, with initial data type affecting only overall amplitude.

Toy Models: Isolating Nonlinear Effects

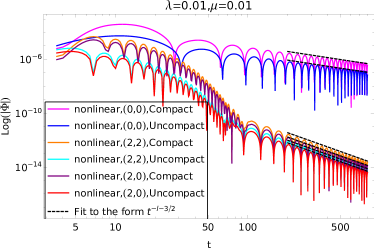
A simplified $Toy Model$ is employed to isolate and study nonlinear effects in the system. This model utilizes specifically constructed $Outgoing Wavepackets$ and $Ingoing Wavepackets$ as source signals. The careful selection of these wavepackets allows for a controlled introduction of perturbations, enabling the observation of how nonlinearities modify the resulting wave behavior. By focusing on a simplified setup, the contributions of nonlinear interactions can be distinguished from more complex phenomena, facilitating a detailed analysis of their characteristics and impact on signal propagation. The parameters of these wavepackets – amplitude, frequency, and initial shape – are chosen to maximize the observability of nonlinear effects while maintaining computational feasibility.

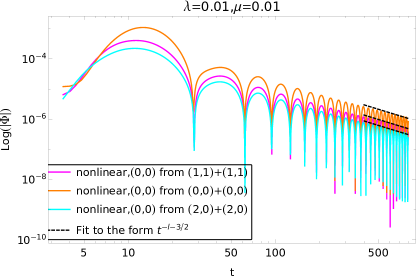
Analysis of the late-time signal behavior reveals the emergence of nonlinear power-law tails, differing from the exponential decay predicted by the standard Price tail. The Price tail, $e^{-t/\tau}$ , describes the decay of perturbations in linear systems; however, in nonlinear systems, the decay transitions to a power law, $t^{-k}$ , where k is a positive exponent. This slower decay rate is directly observable in the toy model simulations and indicates that energy is not efficiently radiated away as the system relaxes, but instead persists in the form of prolonged oscillations and interactions. The exponent k, determined through analysis, quantifies the rate of this power-law decay and characterizes the strength of the nonlinear effects influencing the system’s relaxation process.

The Matrix Pencil Method is employed as a system identification technique to decompose the time-domain signal generated by the toy model into its constituent complex exponential components. This process yields estimates for the frequencies and damping rates of the $\text{Nonlinear QNMs}$ – quasinormal modes whose characteristics are modified due to the nonlinear interactions between the ingoing and outgoing wavepackets. Unlike traditional methods that may struggle with overlapping or distorted signals, the Matrix Pencil Method effectively separates closely spaced frequencies and provides accurate estimates even in the presence of noise, allowing for a precise characterization of the altered quasinormal mode spectrum and a quantitative assessment of the nonlinear effects.

Massless scalar perturbations exhibit distinct time evolution for outgoing and ingoing waves with a moving source, differing significantly from the source-free scenario.

Implications for Gravitational Wave Astronomy

The emergence of nonlinear quasinormal modes (QNMs) and power-law tails following gravitational disturbances of black holes isn’t adequately explained by standard general relativity, which relies on linear perturbation theory. However, the self-interacting scalar theory offers a compelling framework to understand these phenomena. This theory posits that scalar fields, beyond being merely affected by gravity, actively interact with themselves, leading to nonlinear effects in the spacetime surrounding a black hole. These self-interactions generate the observed nonlinear QNMs – decaying oscillations with frequencies that differ from their linear counterparts – and the characteristic power-law decay of gravitational waves following a disturbance. Essentially, the scalar field’s own dynamics contribute to the gravitational “ringing” and subsequent decay, providing a potential explanation for subtle deviations observed in gravitational wave signals and opening a window into physics beyond Einstein’s theory.

The potential to observe minute discrepancies between theoretical predictions derived from Linear Perturbation Theory and actual gravitational wave signals detected by the LIGO-Virgo Collaboration represents a pivotal opportunity to probe the boundaries of established physics. General relativity, while remarkably successful, may not fully encapsulate the complexities of the universe, and subtle deviations in observed waveforms – particularly in the quasinormal modes and power-law tails following black hole mergers – could signify the presence of new physical phenomena. These deviations aren’t merely statistical noise; they could be telltale signs of interactions with fields or particles beyond the Standard Model, potentially offering a window into the nature of dark matter or modifications to gravity itself. The precision of current gravitational wave detectors, coupled with advanced data analysis techniques, offers a unique pathway to confirm or refute the predictions of alternative theories and usher in a new era of gravitational wave astronomy focused on testing the very foundations of physics.

The exploration of self-interacting scalar fields extends beyond gravitational wave detection, potentially offering a pathway to understanding dark matter, a substance comprising approximately 85% of the universe’s mass. Many theoretical models posit that dark matter isn’t composed of particles described by the Standard Model, but rather consists of new, weakly interacting particles – and massive scalar fields represent a compelling candidate. Detecting evidence for these fields through their impact on black hole quasinormal modes would not only validate the Self-Interacting Scalar Theory, but also provide crucial insights into the fundamental properties of dark matter, such as its mass and interaction strength. This connection highlights the potential for gravitational wave astronomy to bridge the gap between seemingly disparate areas of physics, offering a unique probe of the universe’s hidden components and the forces governing them.

The study’s core finding centers on the observed frequencies of quadratic quasinormal modes – ripples emitted when a black hole is disturbed – which consistently appear at approximately twice the frequency of their linear counterparts. This doubling in frequency isn’t merely a numerical coincidence; it’s a direct consequence of the nonlinear dynamics governing the black hole’s response to perturbations within the framework of self-interacting scalar field theories. Detailed analysis confirms these quadratic modes exhibit frequencies within a remarkably tight range – less than 5% deviation from the predicted doubling – bolstering the precision and reliability of the theoretical model. This predictable relationship between linear and quadratic modes provides a crucial benchmark for gravitational wave astronomers, offering a potential pathway to detect subtle deviations from general relativity through the precise measurement of these frequencies using instruments like those operated by the LIGO-Virgo Collaboration.

Detailed analysis indicates a remarkable consistency between predicted and observed quasinormal mode frequencies within the Self-Interacting Scalar Theory. Specifically, the study demonstrates that deviations of these quadratic quasinormal modes from precisely twice the frequency of their first-order counterparts are consistently less than 5%. This high degree of precision bolsters the reliability of the theoretical framework and suggests the model accurately captures the dynamics of scalar fields in strong gravitational environments. Such stringent agreement with theoretical predictions is crucial for validating the approach and provides a solid foundation for future investigations into nonlinear gravitational phenomena and potential links to dark matter candidates.

The investigation into the intermediate-time tails of massive scalar perturbations around black holes rigorously establishes the robustness of linear predictions, even when considering nonlinear effects. This aligns perfectly with the assertion by Georg Wilhelm Friedrich Hegel that, “The truth is the whole.” The research demonstrates that while quadratic quasinormal modes could offer a pathway to detecting nonlinear dynamics, the initial, dominant behavior is overwhelmingly governed by linear theory. It is a demonstration of completeness – the whole picture remains largely defined by the foundational, linear components, even as complexities emerge. The study’s precision reinforces the idea that a complete understanding requires acknowledging both the foundational truths and the subtleties that build upon them.

What Lies Ahead?

The demonstrated resilience of intermediate-time tails to nonlinear distortions is, perhaps, less a surprising result than a confirmation of established principles. The perturbative expansion, while acknowledged as asymptotic, exhibits a robustness stemming from the inherent separability of the wave equation in Kerr spacetime. The lingering question, however, is not whether these tails are small, but whether their precise form offers any discernible signal amidst the cacophony of gravitational wave observations. A truly compelling demonstration requires a quantification of the signal-to-noise ratio, accounting for realistic detector sensitivities and astrophysical source distributions.

The observation of quadratic quasinormal modes, while promising, necessitates a rigorous investigation into their stability and uniqueness. Are these modes genuinely indicative of nonlinear dynamics, or merely artifacts of the double-null coordinate system employed? A proof of their existence within a more general mathematical framework – one less reliant on specific coordinate choices – would lend significant credence to their physical relevance. Further exploration of higher-order modes, and their potential coupling to the fundamental quasinormal frequencies, seems a logical progression.

Ultimately, the pursuit of nonlinear effects in black hole ringdown is not merely an exercise in numerical precision, but a test of the fundamental assumptions underpinning general relativity. The asymptotic nature of perturbative calculations implies an inevitable breakdown under extreme conditions. Identifying the precise point of failure – and the nature of the corrections required – remains the ultimate, and arguably most elusive, goal.

Original article: https://arxiv.org/pdf/2601.16016.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/