Author: Denis Avetisyan
This review details a new theoretical approach for characterizing how fluctuations at the mesoscale fundamentally shape the behavior of complex systems and influence phase transitions.
A generalized framework utilizing weighted Hilbert spaces and quasiaverages is developed to describe thermodynamic potentials in heterophase systems experiencing mesoscopic fluctuations.
Conventional statistical descriptions often struggle to fully capture localized variations occurring at intermediate scales within complex systems. This is addressed in ‘Mesoscopic Fluctuations in Statistical Systems’, which introduces a theoretical framework for characterizing these mesoscopic fluctuations – deviations larger than interparticle spacing yet smaller than the overall system size – and interpreting them as emergent phenomena within a host phase. The paper demonstrates how these fluctuations impact thermodynamic potentials and phase transitions across diverse materials, from condensed matter to biological systems, utilizing concepts like weighted Hilbert spaces and quasiaverages. Could a unified understanding of mesoscopic fluctuations reveal previously hidden connections between seemingly disparate physical and social phenomena?
The Architectures of Possibility: Phase Space and Statistical Systems
The investigation of complex materials fundamentally relies on characterizing the statistical system governing their behavior and meticulously mapping its possible states within a defined PhaseSpace. This space isn’t merely a geometric construct; it represents every conceivable configuration the material can adopt, from atomic arrangements to energy levels. Defining this space is the crucial first step, as it provides the arena in which probabilities are assigned to each state. A comprehensive understanding of the PhaseSpace allows researchers to predict the material’s response to external stimuli, identify potential phase transitions, and ultimately, unlock its unique properties. It is within this mathematical landscape that the emergent behaviors of complex systems – magnetism, superconductivity, and plasticity, for example – can be rigorously analyzed and, potentially, harnessed.
The behavior of any complex system isn’t predictable through simply knowing all its possible states; instead, a ProbabilityDistribution dictates the relative likelihood of observing each one. This distribution isn’t random; it arises from the system’s inherent properties and interactions, shaping which states are more frequently populated over time. Consider a collection of spins in a magnetic material: while each spin could theoretically point in any direction, the distribution will favor alignments that minimize energy, leading to emergent properties like magnetization. P(x), representing the probability of finding the system in state x, is therefore central to understanding macroscopic behavior from microscopic origins, and accurately characterizing this distribution is a primary goal in statistical mechanics and the study of complex materials.
The HilbertSpace serves as the foundational mathematical arena for depicting the possible states of a complex system, enabling detailed examination of how these states evolve over time. Within this space, each unique configuration of the system-its arrangement of particles, energies, and interactions-is represented as a specific state vector. Rigorous analysis of system dynamics becomes possible through the application of operators and functions within the HilbertSpace, allowing researchers to predict and understand the system’s behavior. Recent investigations, as illustrated by accompanying data, reveal that the frustrated matter phase – a state characterized by competing interactions – persists up to a frustration parameter of 0.231632, beyond which the system transitions to a different, less ordered configuration. This precise determination of the phase boundary is crucial for understanding the stability and properties of frustrated materials.
Beyond Uniformity: Weighted and Fibered Spaces
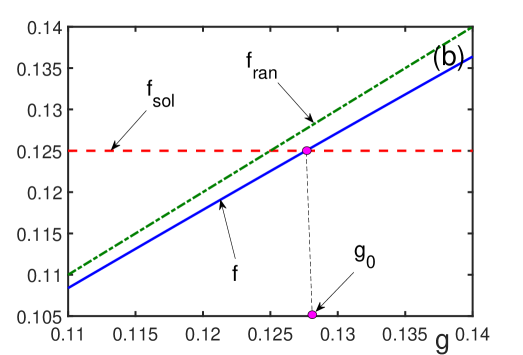
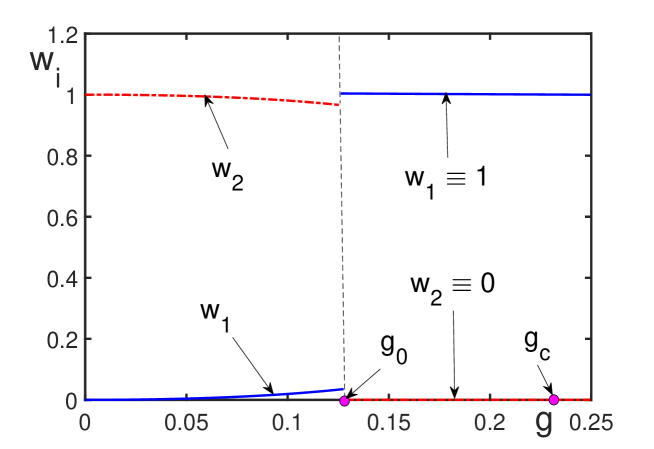
WeightedPhaseSpace and WeightedHilbertSpace constructions address scenarios where not all states within a system are equally probable. These spaces assign a weighting factor, w_i, to each state |\psi_i\rangle, influencing calculations of probabilities and expectation values. Standard inner products are modified to incorporate these weights; for example, the probability of observing state |\psi_i\rangle becomes proportional to w_i|\langle\psi_i|\psi\rangle|^2, where |\psi\rangle represents the system’s state. This allows for the modeling of biased systems or those subject to external influences that favor certain configurations, providing a more accurate representation than traditional, unweighted phase and Hilbert spaces.
The FiberedHilbertSpace provides a mathematical framework for representing physical systems characterized by distinct ThermodynamicPhase regions. This is achieved by constructing a new Hilbert space as the direct sum of individual Hilbert spaces, each corresponding to a specific phase. Formally, if \mathcal{H}_i represents the Hilbert space of the i-th phase, the FiberedHilbertSpace is given by \bigoplus_i \mathcal{H}_i . This construction allows for a unified description of the system’s quantum state, acknowledging the possibility of transitions between phases and enabling calculations that account for the system’s behavior across multiple phase boundaries. The approach is particularly useful when dealing with systems where the relevant degrees of freedom differ significantly in each phase, or where the system can occupy multiple phases simultaneously.
The ability to accurately model systems with complex internal structures and phase boundaries is crucial for materials science and engineering. These boundaries, representing distinct thermodynamic phases, significantly influence material properties such as conductivity, magnetism, and mechanical strength. Utilizing a FiberedHilbertSpace allows for the mathematical representation of these multi-phase systems by effectively combining multiple Hilbert spaces, each corresponding to a specific phase or structural region. This approach avoids the limitations of single-phase approximations and enables precise calculations of system behavior across phase transitions and within heterogeneous materials, ultimately improving the prediction and design of materials with targeted properties. \Delta G = \Delta H - T\Delta S is a key equation used in understanding these transitions.
Reducing Complexity: Effective Hamiltonians and Quasiaverages
The Effective Hamiltonian is a technique used to reduce the complexity of many-body quantum mechanical problems by integrating out, or averaging over, irrelevant degrees of freedom. This process yields a simplified Hamiltonian that describes the essential physics of the system, focusing on collective variables or low-energy excitations. Mathematically, this involves constructing an effective potential or operator that encapsulates the influence of the averaged-out degrees of freedom on the remaining, explicitly treated variables. The resulting H_{eff} is not a fundamental Hamiltonian but rather a coarse-grained representation, valid within a specific energy or length scale, and facilitates calculations of observable properties by focusing computational resources on the most pertinent aspects of the system’s behavior.
The Quasiaverage method is a computational technique employed to determine system properties within the framework of an effective Hamiltonian. It functions by incorporating weighting functions – typically expressed as \langle \psi_i | \psi_j \rangle – that quantify the overlap between different states \psi_i and \psi_j. These weighting functions effectively average out contributions from rapidly fluctuating degrees of freedom, retaining only the most significant interactions and resulting in a simplified representation of the system’s behavior. The accuracy of the Quasiaverage method depends on the appropriate selection of these weighting functions, which must accurately reflect the dominant characteristics of the system under investigation and the timescale of the relevant fluctuations.
The Effective Hamiltonian and Quasiaverage methods are applicable to modeling fluctuations within condensed matter systems occurring on timescales between 10^{-{14}} seconds and 10^{-{12}} seconds. This range encompasses dynamic processes where local equilibration, the restoration of internal thermal equilibrium within a subsystem, occurs approximately at 10^{-{13}} seconds. Consequently, these techniques are particularly suited for investigating transient phenomena and non-equilibrium behavior where these characteristic timescales are dominant, allowing for simplification of complex interactions by focusing on the most relevant degrees of freedom during that timeframe.
The Symphony of Imperfection: Mesoscopic Fluctuations and Material Manifestations
Mesoscopic fluctuations, phenomena occurring at length scales between the microscopic and macroscopic, are increasingly recognized as pivotal in determining material behavior. These aren’t simply random disturbances; rather, they represent collective, transient order arising from the interplay of numerous constituent parts within a material. Unlike thermal noise, which averages out, mesoscopic fluctuations can persist and actively shape a material’s properties, influencing everything from electrical resistance and magnetic susceptibility to structural stability. The significance lies in the fact that these fluctuations aren’t limited by the constraints of traditional thermodynamic equilibrium, allowing materials to exhibit behaviors not predicted by classical models. Consequently, understanding and controlling these intermediate-scale variations is becoming crucial for engineering materials with precisely tailored responses to external stimuli and unlocking novel functionalities.
Mesoscopic fluctuations aren’t merely theoretical curiosities; they manifest demonstrably within a range of materials, offering a window into the origins of their defining characteristics. In magnetic materials, these fluctuations influence domain wall motion and magnetization dynamics. Ferroelectric materials exhibit similar behavior, with fluctuations impacting polarization switching. Perhaps most strikingly, superconductors reveal a compelling connection: these fluctuations can effectively raise the critical temperature – the temperature below which a material becomes superconducting – by creating temporary, localized superconducting regions. This phenomenon suggests that superconductivity isn’t always an ‘all-or-nothing’ state, but can be subtly influenced by these intermediate-scale variations, offering potential avenues for designing higher-temperature superconductors and advancing materials science.
The ability to manipulate mesoscopic fluctuations represents a significant frontier in materials science, offering pathways to engineer materials with unprecedented, tailored properties. By understanding how these intermediate-scale variations influence macroscopic behavior-such as conductivity, polarization, or magnetic response-researchers can move beyond simply discovering materials with desired characteristics to actively designing them. This control extends to optimizing performance in existing applications – for example, enhancing the critical temperature of superconductors – and creating entirely new functionalities. Precisely controlling these fluctuations allows for the creation of materials with specific responses to external stimuli, opening doors to innovations in areas like advanced sensors, energy storage, and high-efficiency electronics. The prospect of designing materials at this level promises a future where material properties are not simply discovered, but intentionally crafted to meet the demands of evolving technologies.
The exploration of mesoscopic fluctuations reveals a fundamental truth about all systems: stability is often a temporary condition. This research, by meticulously detailing how these fluctuations impact thermodynamic potentials and phase transitions, doesn’t merely chart the path to instability, but illustrates its inevitability. As Michel Foucault observed, “Where there is power, there is resistance,” a sentiment that mirrors the inherent tension within any system striving for equilibrium. The fluctuations aren’t errors, but expressions of the system’s inherent dynamism, a constant negotiation between order and chaos – a delay of disaster, perhaps, but disaster nonetheless, given enough time.
What Lies Ahead?
The treatment of mesoscopic fluctuations, as detailed within, is not a closing of accounts, but rather a meticulous cataloging of the inevitable. Every commit is a record in the annals, and every version a chapter in understanding how systems deviate from idealized ensembles. The framework presented seeks not to eliminate these deviations – decay is intrinsic – but to account for them, to calculate the tax on ambition that arises from neglecting these subtle, yet pervasive, effects. Future iterations must confront the limitations inherent in quasiaverages; approximations, however elegant, are merely postponements of a reckoning with true complexity.
A critical path forward lies in extending this formalism beyond equilibrium. Heterophase systems, while amenable to this treatment in certain regimes, present a considerable challenge when driven far from stasis. The weighting schemes within Hilbert spaces, currently tuned for thermodynamic potentials, demand re-evaluation under dynamic conditions. Consider, too, the interplay between mesoscopic fluctuations and non-ergodic behavior – systems that fail to fully explore their accessible phase space.
Delaying fixes is a tax on ambition. The ultimate test will not be the ability to predict phase transitions with increasing precision, but to model the graceful degradation of systems as they inevitably succumb to the relentless march of time. The true value of this work lies not in its predictive power, but in its acknowledgement of the fundamental impermanence of all things.
Original article: https://arxiv.org/pdf/2601.15782.pdf
Contact the author: https://www.linkedin.com/in/avetisyan/
See also:
- Best Controller Settings for ARC Raiders
- Donkey Kong Country Returns HD version 1.1.0 update now available, adds Dixie Kong and Switch 2 enhancements
- PS5’s Biggest Game Has Not Released Yet, PlayStation Boss Teases
- Ashes of Creation Rogue Guide for Beginners
- Sega Insider Drops Tease of Next Sonic Game
- When to Expect One Piece Chapter 1172 Spoilers & Manga Leaks
- Fantasista Asuka launches February 12
- Hytale: Upgrade All Workbenches to Max Level, Materials Guide
- If You Like Stranger Things, You’ll Love This Three-Season Sci-Fi Thriller That Launched Five Years Ago Today
- New Netflix Movie Based on Hugely Popular Book Becomes An Instant Hit With Over 33M Hours Viewed
2026-01-26 02:02