Author: Denis Avetisyan
New research explores how observations of ‘twin stars’-pairs of neutron stars with similar masses but differing radii-are refining our understanding of the extreme matter within these cosmic objects.
This review investigates the impact of recent astrophysical data on models of neutron star equations of state, focusing on the existence and properties of hybrid stars exhibiting strong first-order phase transitions between hadronic and quark matter.
The enduring mystery of the densest observable matter remains unresolved, prompting continued exploration of the equation of state governing neutron stars. This is the central focus of ‘Investigating Twin Star Equation of States in Light of Recent Astrophysical Observations’, which systematically explores the parameter space of hybrid equations of state capable of supporting the existence of ‘twin stars’ – compact objects exhibiting distinct mass-radius relationships due to strong first-order phase transitions. By imposing constraints derived from both hydrostatic equilibrium solutions and recent multi-messenger observations, including gravitational wave data from GW170817 and NICER measurements, we establish upper bounds on maximum mass (2.05~M_\odot) and transition densities, ultimately defining a landscape of allowable hybrid star configurations. What implications do these refined constraints hold for our understanding of matter at extreme densities and the ultimate fate of massive stars?
The Density of Delusion: Probing Matter’s Limits
Neutron stars stand as cosmic behemoths, compressing more mass than the Sun into a sphere roughly the size of a city. This incredible density – a consequence of gravitational collapse – creates conditions unattainable in any terrestrial laboratory. Within these stellar remnants, matter is squeezed to densities exceeding 10^{17} kg/m^3, forcing protons and electrons to combine into neutrons, and potentially forming exotic states of matter like quark-gluon plasma. Studying neutron stars, therefore, provides a crucial, albeit indirect, means of probing the fundamental forces governing matter at its most extreme – offering insights into the behavior of matter when it is pushed far beyond the limits achievable on Earth, and revealing clues about the very building blocks of the universe.
The equation of state (EoS) for neutron stars represents a fundamental challenge in modern physics, as it dictates the relationship between pressure and density within these incredibly dense objects. Determining this EoS is not merely an exercise in astrophysics; it’s a probe of the strong nuclear force – one of the four fundamental forces of nature – at densities far exceeding anything achievable in terrestrial laboratories. The behavior of matter within a neutron star’s core, potentially involving exotic phases like quark matter or hyperons, directly influences the star’s structure, mass, and radius. Consequently, precise knowledge of the EoS is essential for interpreting observations of these stellar remnants and, in turn, gaining insights into the fundamental building blocks of matter and the nature of strong interactions at extreme conditions, potentially revealing new physics beyond the Standard Model. P = K\rho^{\gamma} – a simplified representation of an EoS – illustrates how pressure (P) relates to density (ρ), with constants K and γ defining the specific behavior, but the true EoS of neutron stars is vastly more complex.
Despite decades of research, accurately modeling the equation of state (EoS) of neutron stars remains a significant challenge in nuclear physics. The immense gravitational pressures within these stellar remnants compress matter to densities exceeding those found in atomic nuclei, pushing the boundaries of known physics. Current theoretical approaches, ranging from non-relativistic nuclear models to relativistic mean-field theory and increasingly complex many-body calculations, consistently struggle to reconcile predictions with observational constraints – primarily mass and radius measurements. This discrepancy isn’t merely a refinement issue; it indicates a fundamental gap in understanding the strong nuclear force at such extreme densities, leaving open the possibility of exotic forms of matter – like quark-gluon plasmas or hyperonic matter – residing within neutron star cores. Consequently, the internal composition and precise properties of these enigmatic objects remain largely uncertain, hindering a complete understanding of their formation, evolution, and ultimate fate.
The Breaking Point: Seeking a Phase Transition
Within neutron stars, extreme gravitational compression results in densities exceeding those found in atomic nuclei. Under these conditions, the normally confined neutrons and protons comprising hadronic matter may undergo a phase transition to quark matter, a deconfined state where quarks become the primary constituents. This transition is predicated on the concept that baryons, like neutrons and protons, are not fundamental particles but are composed of quarks bound by the strong nuclear force; sufficient density can overcome this binding. The resulting quark matter is theorized to exhibit different properties – notably a softer equation of state – compared to hadronic matter, potentially influencing the overall structure and stability of the neutron star. This transition is not fully understood and remains a key area of research in nuclear astrophysics.
The transition from hadronic matter to quark matter within a neutron star fundamentally changes the star’s equation of state (EoS). This alteration in the EoS directly influences the mass-radius relationship, as the pressure support within the star is modified at high densities. Specifically, a softer EoS resulting from the phase transition predicts a smaller radius for a given mass compared to a purely hadronic star. Observable signatures of this transition could manifest as deviations from standard neutron star cooling curves, glitches in rotational frequency, or measurable effects on gravitational waves emitted during neutron star mergers, providing potential avenues for observational confirmation of quark matter’s existence.
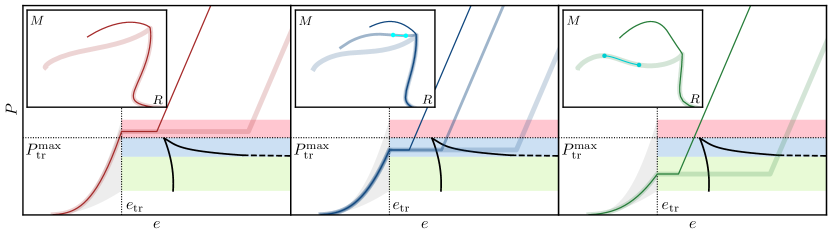
Modeling the extreme conditions within neutron stars requires distinct theoretical approaches for hadronic and quark matter. Chiral Effective Field Theory (ChEFT) provides a framework for describing hadronic interactions at lower densities, while Lattice Quantum Chromodynamics (LQCD) aims to predict the behavior of quark matter at higher densities where perturbative methods fail. This study constrains these models by establishing an upper bound on the transition energy density ( \epsilon_{tre} ) at 1.4 x 1015 g/cm3. This limit, derived from observational data and theoretical analysis, serves as a critical input parameter for both ChEFT and LQCD calculations, refining their predictive power regarding the equation of state and the properties of matter at ultra-high densities.

Mapping the Abyss: Methods for Modeling the Core
Accurate modeling of the hadronic-to-quark matter phase transition within neutron stars necessitates accounting for the coexistence of both phases. This is commonly achieved through the application of Gibbs or Maxwell construction methods. Gibbs construction determines the stable phase at each pressure and density, identifying a mixed phase region where both hadronic and quark matter coexist in equilibrium. The Maxwell construction, conversely, assumes a first-order phase transition with a discontinuous change in energy density and pressure, effectively creating a sharp interface between the two phases. Both methods rely on thermodynamic principles to determine the equilibrium conditions and the resulting equation of state, which is crucial for predicting the properties and stability of neutron stars undergoing this transition.
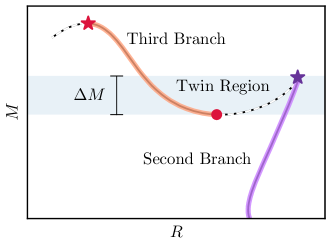
The transition between hadronic and quark matter within neutron stars is characterized by specific values for transition pressure and transition energy density, which dictate the conditions under which this phase change occurs. This study determined a maximum discontinuity in energy density ( \Delta e ) of 2.94 x 1015 g/cm3. This value represents the largest observed difference in energy density across the phase boundary, indicating a significant energy release or absorption during the transition and providing a crucial parameter for accurately modeling the equation of state of dense matter.
The magnitude of the discontinuity in energy density at the phase transition between hadronic and quark matter directly impacts the mechanical stability of neutron stars. A larger \Delta e indicates a more abrupt change in pressure, potentially leading to instabilities such as starquakes or even collapse. This discontinuity is not directly observable, but its effects can be inferred through precise measurements of neutron star oscillations – specifically, the frequencies of their modes – and through observations of gravitational waves emitted during stellar events. The detection of characteristic frequencies or waveforms altered by a substantial energy density discontinuity would provide evidence for the existence of a phase transition within the star’s core, and allow constraints to be placed on the equation of state of dense matter.

Echoes of the Extreme: Connecting Theory to Reality
Neutron stars, remnants of massive stellar collapse, present a unique laboratory for investigating the behavior of matter at extreme densities. Determining the equation of state (EoS) – the relationship between pressure and density – remains a central challenge in nuclear physics. Mass-radius measurements, obtained through observations of pulsar timing and X-ray bursts, constrain the size of these incredibly dense objects, while gravitational wave observations, particularly from neutron star mergers, provide information about their tidal deformability – how easily they are stretched by gravity. These two observational avenues are powerfully complementary; mass-radius data reveal the overall structure, while tidal deformability probes the star’s internal composition and sensitivity to a phase transition from hadronic to potentially exotic matter like quarks. Combining these approaches allows researchers to refine models of the EoS and search for evidence of this transition, ultimately unveiling the fundamental properties of matter under conditions unattainable on Earth.
Tidal deformability-essentially, how much a neutron star bulges or stretches under the gravitational pull of another during a merger-proves a powerful diagnostic of its innermost workings. This property isn’t simply a surface feature; it’s deeply intertwined with the equation of state (EoS) governing matter at extreme densities. A ‘softer’ EoS, indicating more readily compressible matter, results in greater tidal deformation, while a ‘stiffer’ EoS yields less. Consequently, precise measurements of tidal deformability, gleaned from gravitational wave signals emitted during neutron star collisions, allow scientists to constrain the possible EoS and map the internal composition of these stellar remnants. The degree of deformation reveals clues about the presence of exotic matter phases, such as quarks, and helps determine the star’s radius and overall structure, offering a unique window into physics beyond the reach of terrestrial laboratories.
The internal composition of neutron stars remains one of the most compelling mysteries in astrophysics, with a predicted phase transition to quark matter at extreme densities. The existence of ‘hybrid stars’ – those with a core of deconfined quarks surrounded by traditional hadronic matter – offers a potential window into this exotic state. Even more intriguing is the theoretical possibility of ‘twin stars’: pairs with identical masses but differing radii, a direct consequence of this phase transition altering the star’s pressure-mass relationship. Recent research, focusing on observational constraints from gravitational waves and electromagnetic data, has rigorously constrained the maximum mass at which such twin stars could exist. This study establishes an upper limit for the maximum twin star mass, or MTSmax, at 2.05 solar masses, significantly refining the search parameters for these elusive objects and providing crucial insight into the behavior of matter at the densest conditions known in the universe.

Beyond the Horizon: A Multi-Messenger Future
A comprehensive understanding of neutron star interiors necessitates a multi-messenger approach, integrating observations from diverse sources. Gravitational wave detectors, like LIGO and Virgo, provide crucial information about the star’s mass and tidal deformability during mergers, while X-ray telescopes reveal details about the star’s thermal emission and potential pulsations, hinting at its magnetic field structure. Crucially, the detection of neutrinos emitted from neutron star mergers – a feat still awaiting confirmation – would offer a direct probe of the star’s core composition and temperature. By combining these signals, scientists aim to build a holistic picture, constraining the equation of state of ultra-dense matter and potentially unveiling the exotic physics governing these celestial objects-a synergy that transcends the limitations of any single observational technique.
Accurate modeling of neutron star matter demands continuous refinement of theoretical frameworks, increasingly reliant on first-principles calculations like Lattice Quantum Chromodynamics (QCD). These computationally intensive methods offer insights into the strong nuclear force at extreme densities, previously inaccessible to experimentation. However, directly applying Lattice QCD results is challenging; therefore, researchers are employing parameterizations – simplified representations of complex phenomena – to bridge the gap between theory and observation. One promising avenue is the Constant Speed of Sound (CSS) approximation, which assumes a consistent propagation speed for sound waves within the neutron star, reducing the dimensionality of the equation of state (EoS) without sacrificing crucial physics. By combining improved Lattice QCD calculations with realistic parameterizations like CSS, scientists aim to construct more reliable EoS models, ultimately allowing for a more precise interpretation of multi-messenger observations and a deeper understanding of matter under the most extreme conditions in the universe.
The quest to understand matter at extreme densities hinges on unraveling the intricate relationship between the equation of state (EoS), phase transitions within neutron stars, and the potential formation of exotic stellar objects. Current research suggests that as density increases, matter may undergo phase transitions to states beyond ordinary neutrons and protons – potentially including quark matter or hyperons – dramatically altering the star’s EoS. This, in turn, impacts the star’s structure and stability, potentially leading to the creation of “Twin Stars”-objects with similar masses but radically different radii due to distinct internal compositions. Detailed exploration of these connections, combining theoretical modeling with multi-messenger observations, offers a pathway to map the landscape of ultra-dense matter and determine whether the observed neutron stars represent a diverse population of exotic objects, or merely variations within a more standard framework. Confirmation of such exotic stars would not only revolutionize astrophysics but also provide a unique terrestrial laboratory for probing the fundamental nature of quantum chromodynamics.
The pursuit of an equation of state for neutron stars, as detailed in this investigation, echoes a familiar cosmic irony. It attempts to define the boundaries of existence for these stellar remnants, yet the very act of definition seems fleeting. As Nikola Tesla observed, “The universe is an inexhaustible source of energy, but it is also a mirror of our limitations.” The modeling of phase transitions within these stars – the delicate balance between hadronic and quark matter – reveals not mastery over the cosmos, but the exquisite precision with which it exposes the boundaries of current understanding. Each constraint derived from observational data is merely a temporary foothold before the next observation shifts the horizon, reminding one that the cosmos does not yield its secrets easily, and when it does, it often swallows the discovery whole.
Where Do We Go From Here?
The search for constraints on neutron star equations of state, particularly those exhibiting strong first-order phase transitions, reveals a persistent challenge: the mapping of theoretical complexity onto observational reality. Modeling requires consideration of the Tolman-Oppenheimer-Volkoff equation under conditions where the precise nature of ultra-dense matter remains elusive. The existence of ‘twin stars’ – pairs exhibiting correlated properties due to shared origins and composition – offers a compelling observational avenue, yet the signal is fragile, susceptible to systematic errors and the inherent limitations of astrophysical inference.
Future investigations must prioritize a multi-pronged approach. Refinement of theoretical models demands a deeper understanding of quantum chromodynamics in the non-perturbative regime, along with improved treatments of finite-temperature effects and hyperonic interactions. Simultaneously, the observational landscape will benefit from increased sensitivity in gravitational wave detectors and the development of new techniques for electromagnetic spectroscopy, capable of resolving subtle features in neutron star spectra.
One must acknowledge, however, that each new observation, each refined model, simply pushes the horizon of uncertainty further. The true nature of matter at extreme densities may remain forever beyond reach, a humbling reminder that the most elegant theories are, ultimately, just reflections in the event horizon of ignorance.
Original article: https://arxiv.org/pdf/2601.16674.pdf
Contact the author: https://www.linkedin.com/in/avetisyan/
See also:
- Best Controller Settings for ARC Raiders
- Donkey Kong Country Returns HD version 1.1.0 update now available, adds Dixie Kong and Switch 2 enhancements
- PS5’s Biggest Game Has Not Released Yet, PlayStation Boss Teases
- Ashes of Creation Rogue Guide for Beginners
- Sega Insider Drops Tease of Next Sonic Game
- When to Expect One Piece Chapter 1172 Spoilers & Manga Leaks
- Fantasista Asuka launches February 12
- Hytale: Upgrade All Workbenches to Max Level, Materials Guide
- All 6 Takopi’s Original Sin Episodes, Ranked
- 32 Kids Movies From The ’90s I Still Like Despite Being Kind Of Terrible
2026-01-26 17:18