Lost in Translation: How Disorder Simplifies Complex Systems

Author: Denis Avetisyan

New research reveals that random interactions can drive particles on curved surfaces to unexpectedly collapse into lower-dimensional arrangements, revealing a fundamental principle of simplification in complex systems.

Dimensionality reduction applied to a bounded cylinder reveals a system evolving from an initial Gaussian distribution to localized clusters, ultimately organizing into vertically paired arrangements that reflect a residual <span class="katex-eq" data-katex-display="false">\mathbb{Z}_{2}</span> symmetry under 180° rotation, demonstrating how constrained geometry and interaction frustration drive discrete pattern formation from continuous dynamics. — Dimensionality reduction applied to a bounded cylinder reveals a system evolving from an initial Gaussian distribution to localized clusters, ultimately organizing into vertically paired arrangements that reflect a residual $\mathbb{Z}_{2}$ symmetry under 180° rotation, demonstrating how constrained geometry and interaction frustration drive discrete pattern formation from continuous dynamics.

This review examines disorder-induced dimensional reduction on Riemannian manifolds, explaining how particles exhibit glassy relaxation and aging behavior due to rotational diffusion.

While conventional wisdom suggests order requires fine-tuning or external driving, the emergence of structure from purely random interactions remains a compelling paradox. This work, ‘Order Out of Noise and Disorder: Fate of the Frustrated Manifold’, investigates the non-equilibrium dynamics of particles on curved two-dimensional surfaces-spheres, tori, and cylinders-subject to competing random forces. We find that this interplay of disorder and geometry universally leads to disorder-induced dimensional reduction, with particles self-organizing into lower-dimensional structures like bands, rings, or localized clusters. Could this geometric framework provide a novel pathway for understanding emergent spatial order in diverse systems, from spin glasses to astrophysical structure formation?

The Slow Dance of Disorder: Unveiling the Roots of Aging

The phenomenon of aging – a demonstrable slowing of dynamic processes – isn’t limited to biological organisms; it manifests across a surprising range of physical systems, from metallic glasses to magnetic materials and even the flow of granular media. However, pinpointing the underlying mechanisms driving this aging in systems characterized by disorder – those with ‘rugged energy landscapes’ – presents a significant scientific hurdle. Unlike systems with simple, predictable arrangements, these disordered environments introduce complexities that defy traditional analytical methods, making it difficult to predict how – and at what rate – their dynamics will eventually slow. Understanding how quenched disorder fundamentally alters the aging process is therefore crucial for not only accurately modeling these complex systems, but also for potentially manipulating their long-term behavior and harnessing emergent properties.

The aging observed in diverse physical systems – from glasses to magnetic materials – stems not from inherent degradation, but from the intricate topography of their energy landscapes. These landscapes are ‘rugged’ due to ‘quenched disorder’, meaning the system is frozen into a specific, disordered configuration. This creates a multitude of local energy minima, trapping the system and slowing its exploration of potential states. Consequently, traditional analytical methods, designed for smooth, predictable environments, struggle to accurately model the system’s dynamics; these approaches often fail to capture the long-lived, non-equilibrium behavior arising from the system becoming stuck in these numerous minima. Understanding how a system navigates this complex terrain is therefore paramount to predicting its aging characteristics and unraveling the emergent phenomena observed over time.

Accurate modeling of complex energy landscapes is paramount to forecasting the long-term evolution of diverse physical systems. These landscapes, characterized by numerous local minima and barriers, dictate how a system explores its possible states and ultimately ages. Simulations and theoretical frameworks that faithfully capture the ruggedness and heterogeneity of these landscapes allow researchers to predict not only the slowing of dynamics associated with aging, but also the emergence of novel behaviors. By meticulously mapping these landscapes, scientists can uncover hidden relationships between microscopic interactions and macroscopic properties, potentially revealing universal principles governing the aging process across a wide range of materials and phenomena – from the creep of metallic glasses to the folding of proteins and even the dynamics of neural networks. The fidelity of these models directly impacts the ability to extrapolate behavior beyond experimentally accessible timescales, unlocking insights into the ultimate fate and functional limits of complex systems.

Rotational dynamics simulations of <span class="katex-eq" data-katex-display="false">\mathbb{N}=400</span> particles reveal ballistic motion (<span class="katex-eq" data-katex-display="false">\alpha \approx 2.0</span>) characterized by large-amplitude fluctuations in cumulative rotation (<span class="katex-eq" data-katex-display="false">\langle\Theta_{\theta}\rangle = 45.8</span>, <span class="katex-eq" data-katex-display="false">\sigma = 243.8</span>), independent per-cluster rotations, weak anti-correlations between clusters (ρ ≈ -0.06 to -0.21), a rapid autocorrelation decay (τ < 0.2), and a transition from a high-fluctuation formation phase (<span class="katex-eq" data-katex-display="false">\sigma = 228</span>) to a steady state (<span class="katex-eq" data-katex-display="false">\sigma = 244</span>). — Rotational dynamics simulations of $\mathbb{N}=400$ particles reveal ballistic motion ( $\alpha \approx 2.0$ ) characterized by large-amplitude fluctuations in cumulative rotation ( $\langle\Theta_{\theta}\rangle = 45.8$ , $\sigma = 243.8$ ), independent per-cluster rotations, weak anti-correlations between clusters (ρ ≈ -0.06 to -0.21), a rapid autocorrelation decay (τ < 0.2), and a transition from a high-fluctuation formation phase ( $\sigma = 228$ ) to a steady state ( $\sigma = 244$ ).

Simulating the Dance: A Framework for Understanding Dynamic Constraints

Langevin Dynamics is employed to simulate the movement of particles within disordered systems by integrating Newton’s equations of motion with randomly fluctuating forces and a frictional drag term. These stochastic forces, representing thermal fluctuations and other environmental interactions, are modeled as Gaussian white noise with zero mean and a variance proportional to the temperature and friction coefficient, as defined by the fluctuation-dissipation theorem. The frictional drag term, proportional to the particle’s velocity, accounts for energy dissipation due to interactions with the surrounding medium. This approach accurately captures the effects of both deterministic and random forces on particle trajectories, enabling the study of dynamic processes in complex, disordered environments where traditional molecular dynamics may be computationally prohibitive or inaccurate due to the need to explicitly resolve all degrees of freedom.

The simulation framework employs Riemannian Manifolds – the Sphere, Torus, and Bounded Cylinder – to impose specific geometric constraints on particle dynamics. These manifolds are defined by their intrinsic curvature and connectivity, influencing particle movement and interaction. The Sphere ( $S^2$ ) represents a closed, positively curved surface, restricting particles to its exterior and influencing diffusion rates. The Torus ( $T^2$ ) provides a flat, periodic boundary condition, simulating dynamics on an infinite surface with repeating geometry. Finally, the Bounded Cylinder combines aspects of both, offering a flat surface with periodic boundaries in one dimension and closed boundaries in the other, enabling the investigation of confinement effects on particle behavior. Projecting the dynamics onto these manifolds allows for controlled examination of how geometric constraints affect system evolution and aging characteristics.

Simulating particle trajectories within the defined geometric constraints allows for direct observation of system evolution over time. Data obtained from these trajectories, including particle positions and velocities, are used to calculate time-dependent properties such as the mean squared displacement and the velocity autocorrelation function. Analysis of these properties reveals the system’s aging behavior, specifically the transition from ballistic to diffusive motion and the establishment of a non-equilibrium steady state. The rate of this transition and the characteristics of the steady state are quantified, providing insights into the underlying mechanisms governing the system’s dynamics and how they are influenced by the curved space geometry. Further analysis focuses on identifying any time-dependent changes in these properties, indicative of structural rearrangements or changes in the effective potential experienced by the particles.

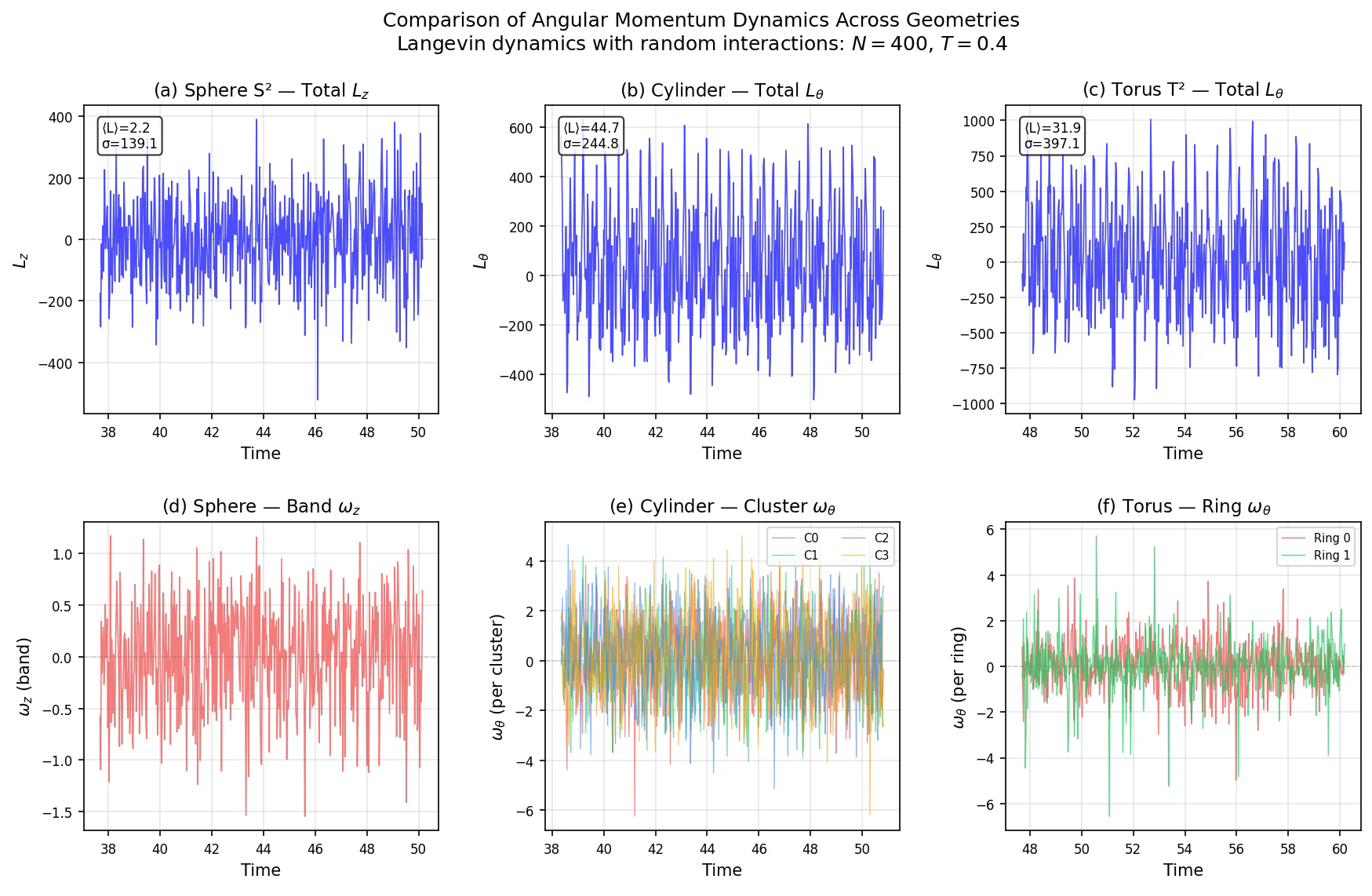
Langevin dynamics simulations (<span class="katex-eq" data-katex-display="false">N=400</span>, <span class="katex-eq" data-katex-display="false">T=0.4</span>) of sphere, cylinder, and torus geometries reveal a progression from coherent rotational behavior in spheres (<span class="katex-eq" data-katex-display="false">\langle\Theta_{z}\rangle=-9.6</span>, <span class="katex-eq" data-katex-display="false">\sigma=148.7</span>), to weakly anti-correlated fluctuations within four clusters in cylinders (<span class="katex-eq" data-katex-display="false">\langle\Theta_{\theta}\rangle=45.8</span>, <span class="katex-eq" data-katex-display="false">\sigma=243.8</span>), and finally to two weakly anti-correlated rings in tori (<span class="katex-eq" data-katex-display="false">\langle\Theta_{\theta}\rangle=80.5</span>, <span class="katex-eq" data-katex-display="false">\sigma=396.0</span>, <span class="katex-eq" data-katex-display="false">\rho=-0.27</span>). — Langevin dynamics simulations ( $N=400$ , $T=0.4$ ) of sphere, cylinder, and torus geometries reveal a progression from coherent rotational behavior in spheres ( $\langle\Theta_{z}\rangle=-9.6$ , $\sigma=148.7$ ), to weakly anti-correlated fluctuations within four clusters in cylinders ( $\langle\Theta_{\theta}\rangle=45.8$ , $\sigma=243.8$ ), and finally to two weakly anti-correlated rings in tori ( $\langle\Theta_{\theta}\rangle=80.5$ , $\sigma=396.0$ , $\rho=-0.27$ ).

Emergent Order: Dimensional Reduction and Structural Motifs

Simulations demonstrate a consistent pattern of dimensional reduction in particle dynamics, indicating that particle movement is not uniformly distributed across the entire simulated manifold. Analysis of particle trajectories reveals increasing confinement to lower-dimensional regions, effectively decreasing the number of independent variables required to describe the system’s evolution over time. This reduction is observed across various manifold geometries and is quantified by measuring the variance of particle positions along each principal dimension; significant decreases in variance along certain dimensions indicate dimensional reduction. The effect is not a result of external constraints but emerges intrinsically from the particle interactions and the manifold’s geometry.

Simulations consistently demonstrate the emergence of specific structural formations dependent on the underlying manifold geometry. On a spherical manifold, particle dynamics result in the formation of concentrated bands; on a bounded cylinder, particles coalesce into distinct clusters; and on a toroidal manifold, particles organize into ring-like structures. These formations are not random occurrences but rather stable, reproducible patterns observed across multiple simulation runs, indicating a direct relationship between manifold topology and emergent system behavior. The dimensions of these structures-band width, cluster size, and ring radius-are quantifiable parameters influenced by simulation parameters and manifold characteristics.

The observed structural formations – bands, clusters, and rings – indicate a reduction in the effective degrees of freedom of the particle system. As particles become constrained to these lower-dimensional manifolds, their movement is limited to within the structure, effectively decreasing the number of independent variables required to describe the system’s state. This simplification of dynamics is not a result of external forces, but rather an emergent property of the system itself, where self-organization leads to constrained motion and a corresponding decrease in the complexity of the overall particle behavior. The system, therefore, operates with a reduced computational burden as it navigates these simplified spaces.

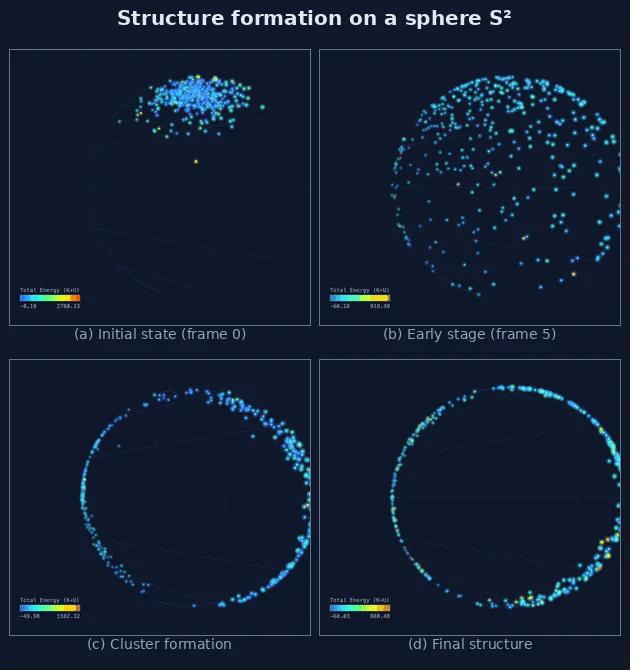
Dynamic dimension reduction successfully transforms an initial Gaussian distribution on a 2D sphere <span class="katex-eq" data-katex-display="false">S^2</span> into a quasi-one-dimensional band on a 1D ring <span class="katex-eq" data-katex-display="false">S^1</span>, as visualized by energy-dependent color mapping. — Dynamic dimension reduction successfully transforms an initial Gaussian distribution on a 2D sphere $S^2$ into a quasi-one-dimensional band on a 1D ring $S^1$ , as visualized by energy-dependent color mapping.

The Slowing Dance: Linking Structure to the Essence of Aging

The emergence of organized structure within a system isn’t merely a visual phenomenon; it’s fundamentally linked to a deceleration of dynamic processes, mirroring the characteristics of aging. Research demonstrates that as a system undergoes dimensional reduction – effectively limiting the space available for particle movement – its dynamics demonstrably slow. This isn’t simply a matter of fewer degrees of freedom, but a correlation where the formation of these low-dimensional configurations actively constrains particle trajectories. The system’s tendency to settle into these restricted spaces creates a kind of ‘structural viscosity’, impeding the exploration of the full range of possible states and ultimately leading to a progressive slowing of activity that defines the aging process. This interplay between structure and slowed dynamics offers a crucial insight into how systems transition from fluid exploration to constrained, aging states.

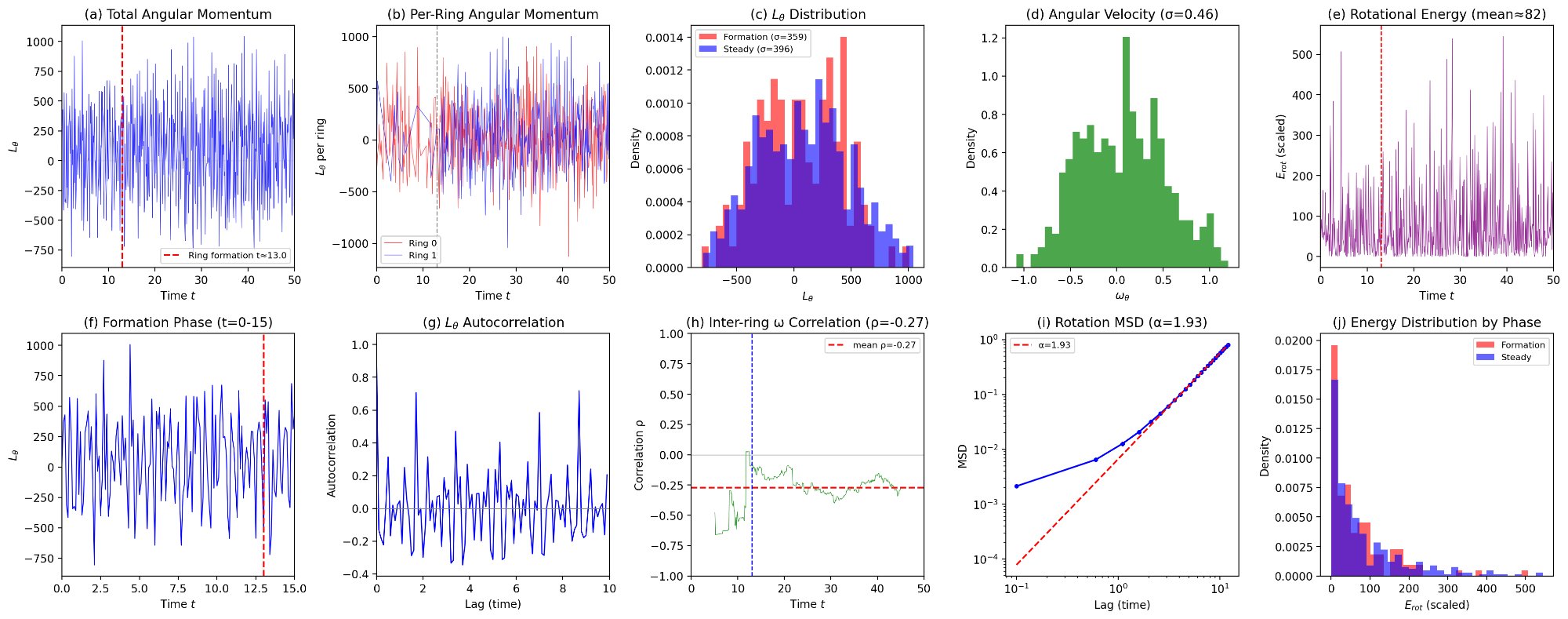
The system’s progression towards lower-dimensional configurations isn’t merely a structural change, but a dynamic process that actively restricts particle movement. As the system evolves, it increasingly favors these constrained spaces, effectively creating ‘traps’ that limit the accessible regions for particles. This isn’t a complete immobilization, but rather a significant reduction in the phase space available for exploration; particles become confined to increasingly smaller and specific pathways. Consequently, the ability to sample the full range of possible states diminishes, leading to slower dynamics and the characteristic aging behavior observed. The extent of this confinement varies with the underlying geometry, as evidenced by anomalous diffusion exponents – a value approaching 1.0 indicates highly constrained motion, while values closer to 2.0 suggest greater, though still limited, freedom.

The observed slowing of dynamics, characteristic of aging in this system, is effectively explained by a ‘trap model’ wherein the system becomes increasingly confined to limited configurations over time. Analysis reveals anomalous diffusion exponents that quantify this constrained motion, varying significantly based on the underlying geometry; particles exhibit near-immobility on the sphere ( $\alpha \approx 1.0$ ), increased but still limited movement on the torus ( $\alpha \approx 1.7$ ), and the most freedom – though still anomalous – on the cylinder ( $\alpha \approx 2.0$ ). These exponents demonstrate that the system isn’t simply slowing down uniformly, but rather becoming topologically constrained, with the geometry of the space actively influencing the degree to which particles are trapped and unable to explore the full range of possible states, ultimately manifesting as the observed aging behavior.

Analysis of <span class="katex-eq" data-katex-display="false">N=400</span> particles undergoing rotational dynamics reveals superdiffusive behavior (<span class="katex-eq" data-katex-display="false">\alpha \approx 1.9</span>) characterized by large-amplitude fluctuations in cumulative rotation, rapid autocorrelation decay (<span class="katex-eq" data-katex-display="false">\tau < 0.2</span>), and a negative inter-ring correlation (<span class="katex-eq" data-katex-display="false">\rho = -0.27</span>), indicating a transition from formation to a steady state with mean rotational energy of approximately 82. — Analysis of $N=400$ particles undergoing rotational dynamics reveals superdiffusive behavior ( $\alpha \approx 1.9$ ) characterized by large-amplitude fluctuations in cumulative rotation, rapid autocorrelation decay ( $\tau < 0.2$ ), and a negative inter-ring correlation ( $\rho = -0.27$ ), indicating a transition from formation to a steady state with mean rotational energy of approximately 82.

Beyond the Simulation: Towards a Universal Theory of Aging

Rigorous theoretical validation bolsters the understanding of aging processes within these disordered systems. Employing advanced analytic techniques – specifically the Mode-Selective Randomly Jagged Distribution (MSRJD) and Dynamical Mean-Field Theory (DMFT) – researchers have successfully corroborated simulation results, establishing a robust theoretical framework. These calculations confirm the mechanisms driving aging, providing quantitative agreement with observed behaviors and offering insights into the underlying physical principles. The convergence of simulation and theory not only solidifies the findings but also allows for predictive modeling and a deeper exploration of the complex interplay between structure, dynamics, and time-dependent properties in these materials; this analytical support transforms empirical observations into a fundamentally understood phenomenon.

The observed link between dimensional reduction and structure formation during aging appears to transcend the limitations of the specific disordered systems initially investigated. Analyses indicate that as these materials age, their effective dimensionality decreases, effectively simplifying the pathways available for particle rearrangement and contributing to the slowdown of dynamics. This isn’t merely a characteristic of the studied geometries, but rather a fundamental process potentially governing aging in a broad spectrum of disordered materials – from granular media and colloidal suspensions to glasses and even certain biological tissues. The implication is that a common underlying mechanism – the progressive restriction of accessible configurations through structure formation and effective dimensional reduction – may explain the ubiquitous phenomenon of aging across diverse physical systems, offering a unifying principle for understanding their long-term behavior.

Investigations are now directed towards leveraging these established principles to construct models of increasingly intricate physical systems, moving beyond the initial geometries explored. This expansion aims to determine the universality of the observed aging mechanisms – specifically, the roles of Dimensional Reduction and emergent structure – across a broader spectrum of disordered materials. Potential applications extend into materials science, where understanding and controlling aging processes could lead to the design of more durable and reliable materials, and potentially inform advancements in fields like granular mechanics, geophysical flows, and even the behavior of complex fluids, ultimately bridging fundamental research with practical technological innovation.

The study illuminates a fascinating convergence between geometry and dynamics, revealing how disorder can fundamentally alter the effective dimensionality of a system. This echoes John Stuart Mill’s assertion that “It is better to be a dissatisfied Socrates than a satisfied fool,” as the researchers don’t simply accept the initial complexity of the disordered manifold. Instead, they probe deeper, revealing a simplified, lower-dimensional structure emerging from the noise. The collapse onto lower-dimensional structures isn’t merely a mathematical curiosity; it represents a fundamental shift in the system’s behavior, much like recognizing the limitations of a superficially satisfying, yet ultimately incomplete, understanding of the world.

Where Do the Curves Lead?

The observation of disorder-induced dimensional reduction-particles collapsing from complex surfaces to lower-dimensional arrangements-presents a disquieting echo of systems far removed from purely physical inquiry. It suggests a principle at play where complexity, when sufficiently perturbed, does not necessarily increase in its exploration of phase space, but actively seeks simpler configurations. This begs the question: to what extent does this represent a fundamental tendency toward minimal energetic states, or a consequence of the limited resolution with which systems are observed? The inherent challenge lies in distinguishing true collapse from merely appearing so, given the scale of investigation.

Future work must address the limitations of current approaches. The study of non-equilibrium dynamics on manifolds has, thus far, largely focused on idealized geometries. Exploring more realistic, topologically complex surfaces-those mirroring biological structures or heterogeneous materials-will be crucial. Further investigation into the role of rotational diffusion and aging processes, beyond the scope of this work, could reveal whether these phenomena accelerate or inhibit the observed collapse. It is increasingly clear that the algorithms used to model these systems are not neutral observers, but active participants in shaping the observed outcomes.

Ultimately, the field faces a critical juncture. It must move beyond simply describing the reduction in dimensionality to understanding the underlying mechanisms that dictate which dimensions are lost, and the consequences for the system’s long-term behavior. The choice of coordinate systems, the implementation of stochastic rules-these are not merely technical details, but encode assumptions about the nature of reality itself. Transparency is minimal morality, not optional.

Original article: https://arxiv.org/pdf/2601.18653.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/