Black Hole Equivalence: When Quantum Gravity Looks Classical

Author: Denis Avetisyan

New research reveals a surprising link between quantum-corrected black hole solutions and those arising from classical gravity with a specific electromagnetic field.

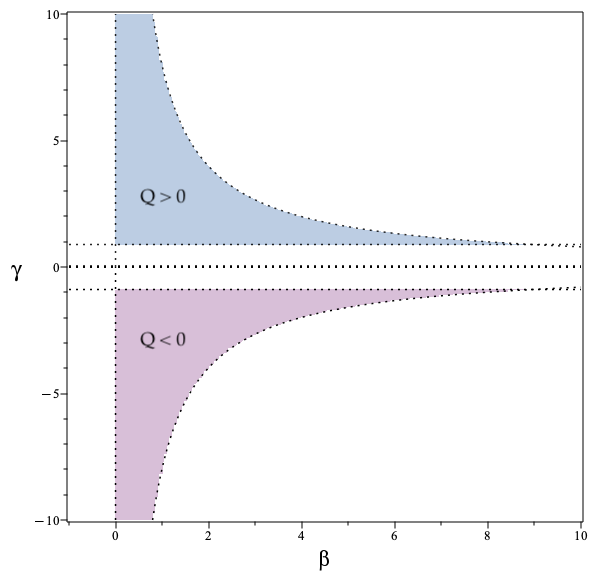
The study demonstrates that thermodynamic stability-defined by simultaneously satisfying local conditions-permits a bifurcated parameter space in terms of β and γ, yielding configurations distinguished by positive or negative electric charge, a relationship that remains structurally consistent despite variations in pressure, temperature, and entropy.

A BTZ black hole solution obtained via quantum backreaction in New Massive Gravity can be exactly reproduced within classical General Relativity coupled to exponential electrodynamics.

The persistent challenge of reconciling quantum effects with classical gravity motivates explorations of emergent spacetime geometries. This is the central theme of ‘Classical emergence of the quantum-backreacted BTZ black hole from exponential electrodynamics’, which demonstrates that a black hole solution previously derived from a semiclassical analysis of New Massive Gravity-characterized by logarithmic asymptotic behavior-can be exactly realized as a solution within classical General Relativity coupled to exponential nonlinear electrodynamics. This correspondence reveals a dynamical equivalence between these seemingly disparate approaches, establishing a mapping between quantum backreaction parameters and classical charges. Does this suggest a broader connection between higher-curvature corrections in quantum gravity and nonlinear electrodynamics, potentially offering new insights into the nature of gravity itself?

The Inevitable Collapse: Where Classical Gravity Fails

General Relativity, elegantly formulated through the Einstein-Hilbert Action, has consistently predicted gravitational phenomena with remarkable precision, from the bending of light around massive objects to the existence of gravitational waves. However, this classical description of gravity encounters fundamental limitations when probing extreme conditions. At singularities – points of infinite density like those within black holes or at the universe’s very beginning – the theory’s predictive power collapses. Furthermore, at incredibly high energies, such as those thought to have existed in the earliest moments of the universe, quantum effects become dominant, and General Relativity, being a purely classical theory, fails to provide an accurate description. These breakdowns signal the necessity of a more comprehensive theory – one that seamlessly integrates gravity with the principles of quantum mechanics, resolving the inconsistencies and offering a robust framework for understanding the universe under all conditions. The inability of General Relativity to account for these scenarios highlights the need to move beyond its classical framework and explore the realm of quantum gravity.

The persistent incompatibility between General Relativity and Quantum Field Theory represents a foundational crisis in modern physics. While General Relativity elegantly describes gravity as the curvature of spacetime, and accurately predicts phenomena at large scales, it operates within a classical framework. Quantum Field Theory, conversely, governs the other three fundamental forces – electromagnetism, the weak nuclear force, and the strong nuclear force – by describing forces as mediated by quantized particles. Attempts to simply apply the rules of Quantum Field Theory to gravity result in nonsensical, infinite values – a sign that the theory breaks down. This disconnect isn’t merely a mathematical inconvenience; it suggests that gravity, at its most fundamental level, may operate according to principles drastically different from those governing all other known forces, necessitating a completely new theoretical framework to reconcile these two pillars of physics.

A complete theory of quantum gravity necessitates grappling with quantum backreaction, the dynamic interplay between quantum fields and the very fabric of spacetime. Classical general relativity describes gravity as a smooth, deterministic curvature of spacetime caused by mass and energy; however, quantum mechanics introduces inherent uncertainties and fluctuations at the smallest scales. These quantum fluctuations aren’t simply disturbances within spacetime, but actively contribute to its geometry, potentially creating a foamy, fluctuating structure. Calculating this backreaction is extraordinarily difficult, requiring a self-consistent solution where the quantum fields influence spacetime, and the modified spacetime, in turn, affects the quantum fields. Understanding this feedback loop is paramount, as ignoring it leads to inconsistencies and divergences in calculations. Current research focuses on effective field theory approaches and semi-classical methods to approximate these effects, seeking to predict how quantum phenomena might alter gravitational behavior and resolve the singularities that plague classical general relativity, potentially revealing the true nature of spacetime at the Planck scale.

Modified Spacetime: A Lower-Dimensional Pathway

New Massive Gravity (NMG) represents a modification of General Relativity specifically formulated for three-dimensional spacetimes. Unlike standard General Relativity, which is based on the Einstein-Hilbert action involving only linear curvature terms, NMG incorporates higher-order curvature corrections, specifically quadratic curvature invariants. These terms, constructed from quantities like the Ricci tensor $R_{\mu\nu}$ , the Ricci scalar $R$ , and the Weyl tensor $C_{\mu\nu\rho\sigma}$ , alter the gravitational dynamics and introduce new degrees of freedom. The resulting field equations are second-order, preserving a well-defined initial value problem, and allow for the propagation of massive gravitons, offering a potential pathway to address inconsistencies arising from quantum gravity considerations in lower dimensions.

New Massive Gravity (NMG) defines gravitational dynamics through the use of Quadratic Curvature Invariants, specifically the $R^2$ , $R_{\mu\nu}R^{\mu\nu}$ , and $R_{\mu\nu\rho\sigma}R^{\mu\nu\rho\sigma}$ terms added to the Einstein-Hilbert action. These invariants, which are second-order contractions of the Riemann curvature tensor, introduce higher-derivative terms into the gravitational equations of motion. This approach differs from standard General Relativity, which relies solely on linear curvature terms. The inclusion of quadratic curvature terms is motivated by the expectation that quantum effects, often involving loop corrections, will introduce such higher-derivative terms into the effective gravitational action, potentially resolving issues with ultraviolet divergences and providing a more complete description of gravity at high energies.

Within New Massive Gravity (NMG), the mass parameter, denoted as $m$ , directly dictates the mass of the graviton, the quantum of gravitational interaction. This mass introduces a screening effect, modifying the range of gravitational interactions; unlike the massless graviton of General Relativity which has infinite range, a massive graviton exhibits a finite range determined by $1/m$ . Consequently, the propagation of gravitational waves is significantly altered, with massive gravitons propagating as damped waves instead of propagating freely. The value of $m$ also influences the overall spacetime geometry, potentially leading to the existence of black holes with different properties than those predicted by General Relativity, and affecting the dynamics of cosmological models.

The BTZ Black Hole: A Testbed for Quantum Corrections

The BTZ black hole provides a crucial theoretical framework for investigating modifications to general relativity due to its analytical solvability in three dimensions. Unlike many black hole solutions requiring numerical methods, the BTZ metric – described by $ds^2 = -(r^2-r_0^2)(dt^2 - dr^2) + r^2 d\phi^2$ – admits exact solutions to Einstein’s field equations. This analytical tractability allows researchers to perform explicit calculations of quantum backreaction effects and explore deviations from classical gravity without the computational challenges associated with more complex spacetime geometries. Consequently, the BTZ black hole serves as a simplified, yet informative, model for studying quantum gravity phenomena and testing theoretical predictions.

A semiclassical approach was utilized to investigate quantum backreaction on the BTZ black hole spacetime by treating gravity classically while quantizing matter fields. This involved coupling quantum fields – specifically, a massless scalar field – to the BTZ background geometry and calculating the expectation value of the stress-energy tensor $\langle T_{\mu\nu} \rangle$ . The resulting stress-energy tensor then serves as a source term in the Einstein equations, leading to deviations from the original BTZ solution. This process effectively models the effect of quantum fluctuations on the spacetime geometry, providing a means to assess the validity of classical general relativity in the presence of quantum effects and allowing for the computation of corrections to the classical metric.

Calculations performed by coupling quantum fields to the BTZ black hole geometry yield a logarithmic correction to the standard BTZ metric. Specifically, the metric deviates from the classical solution via a term proportional to $\log(r)$ , where r represents the radial coordinate. This correction arises from quantum backreaction effects and signifies a modification to the spacetime geometry at smaller scales. The results of these calculations establish a dynamical equivalence, demonstrating that the quantum-corrected BTZ black hole shares the same asymptotic symmetry group as the original BTZ solution, despite the altered metric.

Nonlinear Electrodynamics: Gravity as an Emergent Phenomenon

Nonlinear Electrodynamics (NLED) presents a framework for gravitational physics that diverges from standard General Relativity by modifying the relationship between electromagnetism and spacetime curvature. While General Relativity treats gravity as a purely geometric phenomenon, NLED posits that gravity can be understood as an effective manifestation of nonlinear electromagnetic interactions. This approach offers a distinct pathway for incorporating quantum corrections into gravity, as the nonlinearities within the electromagnetic field can potentially absorb and regulate the divergences that arise in perturbative quantum gravity calculations. Unlike approaches relying on perturbative expansions around a fixed spacetime background, NLED inherently accounts for backreaction effects, where quantum fluctuations of the electromagnetic field modify the spacetime geometry itself, potentially resolving issues related to the breakdown of predictability at extremely high energies or small scales. This framework offers an alternative to string theory or loop quantum gravity for addressing the challenges of quantum gravity.

Exponential Nonlinear Electrodynamics (NLED) offers a means of modeling quantum-backreacted geometry, yielding results consistent with those derived from the Non-Metric Gravitational (NMG) theory. This specific NLED formulation is characterized by the Lagrangian parameter β, which quantifies the strength of the nonlinear terms and directly influences the resulting spacetime geometry. The value of β effectively controls the degree of quantum corrections to the classical gravitational field, allowing for a parameterization of backreaction effects without requiring the full complexity of NMG. Analysis demonstrates that specific values of β can reproduce the same geometric properties – including curvature and metric components – as those calculated using the NMG framework, validating Exponential NLED as an alternative, equivalent approach to incorporating quantum corrections into gravitational models.

The Plebanski formulation offers a particularly useful approach to analyzing Nonlinear Electrodynamics (NLED) due to its ability to recast the field equations as a set of first-order equations. This simplifies the process of finding solutions and deriving thermodynamic properties. Specifically, the scaling weight of NLED couplings, denoted as $ω_n$ , directly determines the form of the resulting thermodynamic relations and dictates the applicability of the first law of thermodynamics to the system. This parameter governs how the NLED couplings transform under a Weyl rescaling of the metric, impacting conserved quantities and the overall thermodynamic consistency of the solution. Consequently, analyzing the $ω_n$ values is crucial for understanding the thermodynamic behavior of spacetimes governed by NLED.

The Fragile Stability of Spacetime: Extended Laws and the Quantum Horizon

The enduring physical relevance of any proposed black hole solution hinges critically on its thermodynamic stability. This isn’t merely a mathematical requirement; it dictates whether the black hole can realistically exist within the framework of general relativity and, crucially, when quantum effects are considered. Instabilities manifest as perturbations that can lead to the black hole’s decay or a dramatic alteration of its event horizon, rendering the solution unphysical. Analyses demonstrate that even seemingly minor modifications to classical black holes, introduced by quantum gravity considerations, can significantly impact their stability. Therefore, rigorous examination of thermodynamic properties – including temperature, entropy, and free energy – is paramount to validating any black hole model and understanding its behavior in the extreme gravitational environments where it resides. The persistent pursuit of stable solutions not only reinforces the foundations of black hole physics but also provides crucial constraints on the development of a consistent theory of quantum gravity.

Black hole thermodynamics, traditionally rooted in concepts like temperature and entropy, requires refinement when considering cosmological influences and quantum effects. The standard framework is extended to incorporate terms accounting for the cosmological constant, a representation of dark energy’s pervasive pressure, ensuring accurate calculations of black hole properties in expanding universes. This extended First Law manifests mathematically through expressions like the Hawking temperature, given by $TH = κs / 2π$ , where $κs$ represents the surface gravity. Simultaneously, the Bekenstein entropy, a measure of the black hole’s disorder, is quantified as $S = 2πκ ΩD-2 rhD-2$ , with $ΩD-2$ denoting the area of the event horizon in D dimensions and $rh$ representing the radius. These additions are not merely mathematical adjustments; they fundamentally alter the understanding of black hole stability and their interaction with the surrounding spacetime, offering crucial insights into the elusive nature of quantum gravity.

Investigations into black hole thermodynamics, particularly concerning their stability and the nuances of extended laws, offer a unique window into the perplexing realm of quantum gravity. By rigorously examining how entropy, temperature – expressed as $TH = κs / 2π$ – and area relate in these extreme gravitational environments, researchers gain crucial insights into how gravity might behave at the quantum level. These analyses aren’t merely theoretical exercises; they probe the very fabric of spacetime, revealing potential mechanisms that maintain its stability even under the most intense conditions. The consistent application of thermodynamic principles to black holes suggests that information, rather than being lost, might be encoded on the event horizon – a concept vital to resolving the information paradox. Ultimately, these studies represent a powerful approach to understanding the fundamental laws governing the universe at its most extreme limits, offering clues about the nature of spacetime and the potential for a unified theory of physics.

The pursuit of dynamical equivalence, as demonstrated in this work concerning the BTZ black hole, highlights a fundamental truth about complex systems. Stability, as presented through classical General Relativity coupled with nonlinear electrodynamics, is merely an illusion that caches well – a temporary ordering arising from specific conditions. This echoes a broader principle: systems aren’t tools, but ecosystems. As Thomas Kuhn observed, “the world does not speak in numbers,” but rather presents itself as a shifting landscape of paradigms. The ability to find classical analogues for semiclassical results isn’t about achieving a final, definitive model, but recognizing the inherent plasticity of the universe and the limitations of any single descriptive framework. Chaos isn’t failure-it’s nature’s syntax.

What Lies Beyond the Horizon?

The demonstration of a classical equivalence for a quantum-backreacted black hole is not an arrival, but a carefully constructed bridge. It reveals, with characteristic elegance, how easily the scaffolding of quantum effects can be absorbed into the architecture of classical fields – a trick the universe has undoubtedly employed countless times. Yet, this absorption does not erase the underlying chaos. The specific nonlinear electrodynamics that permits this classical mimicry is, itself, a constructed solution, a particular island of order in a vast sea of possible fields. The true question is not whether such equivalences exist, but how robust they are to perturbation, to the inevitable imperfections that ripple through any physical model.

This work invites a re-examination of the very notion of ‘classicality’. Is it a fundamental state, or merely a convenient forgetting? Each elegantly solved black hole, each classical limit, represents a temporary reprieve from the underlying complexity. The search for such solutions will continue, of course – every new architecture promises freedom until it demands gravitational wave observatory sacrifices. But the field should also turn its attention to the failures, to the scenarios where these equivalences break down, and to the emergence of genuinely novel phenomena beyond the reach of classical description.

Ultimately, the horizon remains. Not as a barrier to knowledge, but as a constant reminder that order is just a temporary cache between failures. The universe does not solve problems; it merely reshuffles the terms. The value of this work lies not in its solution, but in the deeper questions it provokes, in the acknowledgment that the most interesting physics often lies just beyond the reach of our current tools – and always will.

Original article: https://arxiv.org/pdf/2601.18967.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/