Superconductor Fingerprints Revealed by Current Disentanglement

Author: Denis Avetisyan

A new spectroscopic technique allows researchers to map the electronic structure of superconductors by separating Andreev and quasiparticle currents across tunable junctions.

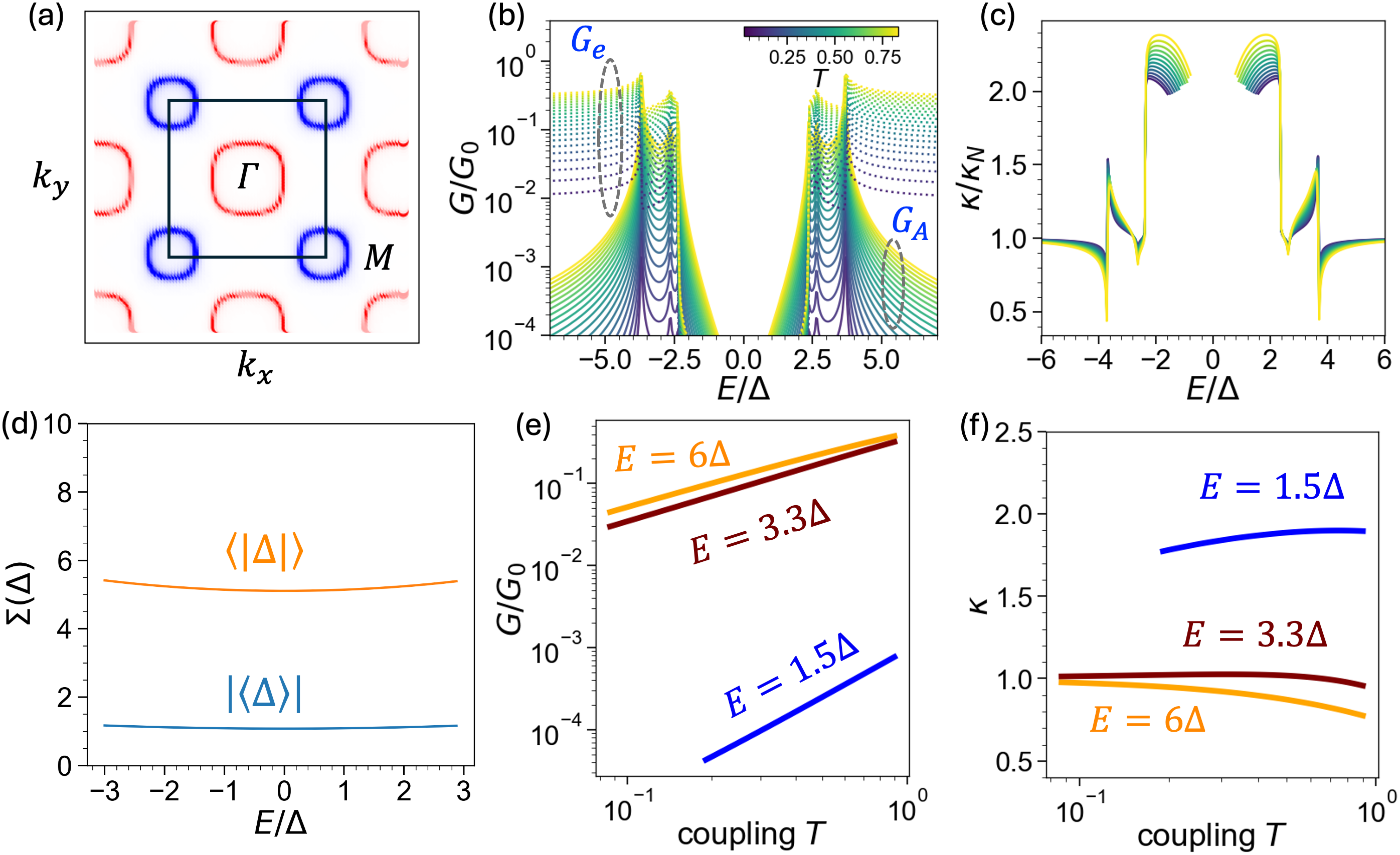
In <span class="katex-eq" data-katex-display="false"> s\pm </span> superconductors, a competition between quasiparticle tunneling and Andreev reflection modulates conductance as a function of energy, maintaining finite superconducting gap values across all energies and demonstrating a scaling relationship between conductance, decay rate, and tip-substrate coupling strength. — In $s\pm$ superconductors, a competition between quasiparticle tunneling and Andreev reflection modulates conductance as a function of energy, maintaining finite superconducting gap values across all energies and demonstrating a scaling relationship between conductance, decay rate, and tip-substrate coupling strength.

Researchers demonstrate that analyzing the coupling-dependent decay rate of tunneling currents can identify superconducting gap symmetry and characterize unconventional superconductors.

Distinguishing superconducting pairing symmetries remains a central challenge in condensed matter physics, particularly for unconventional materials. This is addressed in ‘Fingerprinting superconductors by disentangling Andreev and quasiparticle currents across tunable tunnel junctions’, which demonstrates that Tunneling Andreev Reflection (TAR) spectroscopy can uniquely identify superconducting gap symmetry by analyzing the coupling-dependent decay rate of tunneling currents. Specifically, the additivity of excess decay rate allows for the disentanglement of Andreev and quasiparticle contributions, revealing distinct spectral fingerprints for s-wave, d-wave, and more complex order parameters. Will this approach enable atomically resolved mapping of superconducting states and unlock a deeper understanding of high-temperature superconductivity?

Deconstructing Superconductivity: Peeling Back the Layers

The emergence of superconductivity, where materials conduct electricity with zero resistance, hinges on a remarkably subtle balance between how electrons interact with each other and the formation of what are known as energy gaps. These gaps, arising from quantum mechanical effects, represent a range of energies where no electron states are allowed, effectively hindering the scattering that normally causes resistance. Probing this interplay isn’t straightforward; electron interactions are inherently many-bodied, meaning the behavior of one electron is influenced by all others, and the energy gaps can be incredibly small and sensitive to external conditions. Understanding the precise nature of these interactions – whether they are attractive or repulsive, short-ranged or long-ranged – is crucial to deciphering the mechanisms behind superconductivity, particularly in the more complex, recently discovered materials where simple theories fall short. Ultimately, characterizing this delicate dance between electrons and energy gaps offers the key to designing new materials with enhanced superconducting properties and unlocking their vast technological potential.

Investigating the nuances of superconductivity presents a significant challenge to conventional techniques, especially when examining unconventional materials exhibiting multiple superconducting gaps – a phenomenon denoted as s±. These materials defy simple explanations, as traditional methods, such as angle-resolved photoemission spectroscopy and tunneling measurements, often lack the resolution to disentangle the contributions from each gap. The presence of multiple gaps complicates the energy landscape, creating a complex interplay of electron pairings and interactions that obscure the fundamental mechanisms driving superconductivity. Consequently, researchers are compelled to develop innovative approaches – including advanced spectroscopic techniques and theoretical modeling – to fully map these energy gaps and unravel the intricacies of unconventional superconductivity, potentially unlocking new avenues for materials design and technological applications.

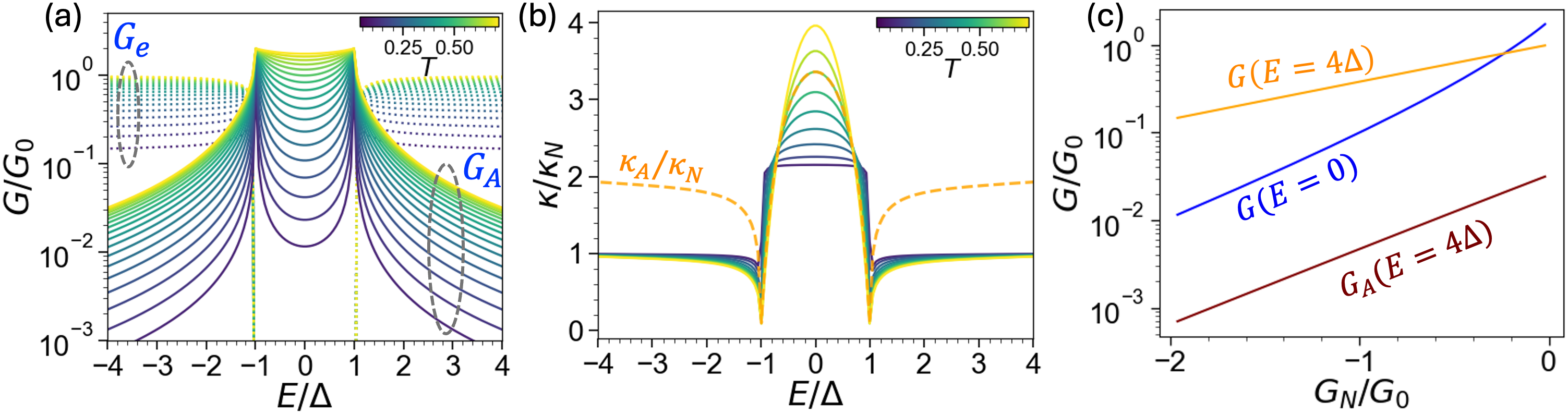
Strong coupling in an s-wave superconductor leads to a near-contact conductance exceeding the expected limit of 2, reaching up to 4 as the mid-gap conductance approaches <span class="katex-eq" data-katex-display="false">2G_0</span>, due to enhanced Andreev reflection relative to tunneling, as demonstrated by spectroscopy of varying tip-substrate coupling strengths <span class="katex-eq" data-katex-display="false">T = |\gamma|^2</span>. — Strong coupling in an s-wave superconductor leads to a near-contact conductance exceeding the expected limit of 2, reaching up to 4 as the mid-gap conductance approaches $2G_0$ , due to enhanced Andreev reflection relative to tunneling, as demonstrated by spectroscopy of varying tip-substrate coupling strengths $T = |\gamma|^2$ .

Tunneling Andreev Reflection: A New Lens on Electronic Behavior

Tunneling Andreev Reflection (TAR) spectroscopy is a surface-sensitive technique used to investigate the superconducting gap, Δ, and the presence of Andreev bound states (ABS) at interfaces. When a quasiparticle tunnels into a superconductor from a normal metal, it can undergo Andreev reflection, forming a retro-reflected hole and a Cooper pair. The resulting excess current, dependent on the density of states near the Fermi level and the superconducting gap magnitude, allows spectroscopic mapping of these electronic states. TAR is particularly effective at probing non-uniform superconductivity and identifying the spatial distribution of ABS, which are sensitive to surface defects, magnetic impurities, and the local pairing symmetry of the superconductor.

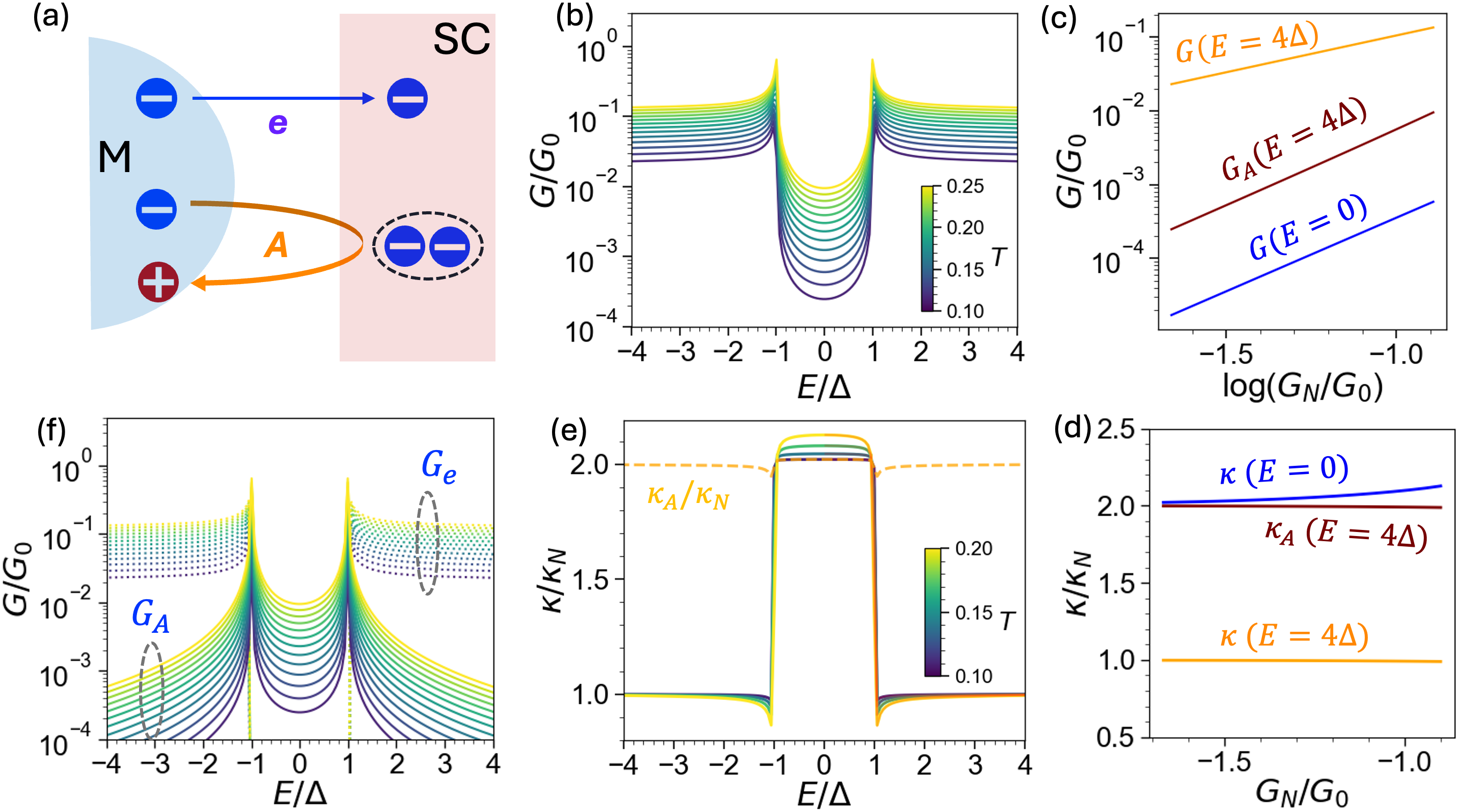
Tunneling Andreev Reflection (TAR) spectroscopy analyzes the decay of the tunneling current between a metallic tip and a superconductor to determine electronic properties. The excess decay rate, beyond that predicted by standard tunneling theory, arises from Andreev reflections – where an electron from the tip is converted into a hole in the superconductor, and vice-versa. The magnitude and temperature dependence of this excess decay rate are directly related to the density of states $N(E)$ near the Fermi level within the superconducting gap. Crucially, the spatial variations and angular dependence of the decay rate can also reveal the symmetry of the superconducting pairing – whether it is s-wave, d-wave, or another symmetry – by mapping the gap’s anisotropy and the distribution of Andreev bound states.

Scanning Tunneling Microscopy (STM) is central to Tunneling Andreev Reflection (TAR) spectroscopy due to its capacity to provide both nanometer spatial resolution and precise control over the tunneling junction. STM operates by scanning a sharp conducting tip across a sample surface while maintaining a constant tunneling current, achieved via a feedback loop controlling the tip-sample separation. This allows for spectroscopic mapping of the sample’s local density of states. Crucially, the STM tip-sample coupling strength – and therefore the tunneling probability – is highly sensitive to tip position and applied bias voltage, enabling researchers to selectively probe Andreev bound states and the superconducting gap with high precision. The technique requires ultra-high vacuum conditions to maintain a clean surface and stable tunneling junction, and typically operates at cryogenic temperatures to minimize thermal noise and enhance the visibility of the relevant spectral features.

The decay rate of conductance for tunneling and Andreev reflection decreases with increasing tip-substrate coupling strength <span class="katex-eq" data-katex-display="false">T=\gamma^{2}</span>, but Andreev reflection maintains a higher excess decay rate-reaching a ratio exceeding 2/1 within the superconducting gap due to contributions from higher-order reflections, as modeled by a fictitious mechanism <span class="katex-eq" data-katex-display="false">C\_{1}G\_{e}^{2}+C\_{2}G\_{e}^{4}</span> with fitted coefficients <span class="katex-eq" data-katex-display="false">C\_{1}= 5.5</span> and <span class="katex-eq" data-katex-display="false">C\_{2}= 11.6</span>. — The decay rate of conductance for tunneling and Andreev reflection decreases with increasing tip-substrate coupling strength $T=\gamma^{2}$ , but Andreev reflection maintains a higher excess decay rate-reaching a ratio exceeding 2/1 within the superconducting gap due to contributions from higher-order reflections, as modeled by a fictitious mechanism $C\_{1}G\_{e}^{2}+C\_{2}G\_{e}^{4}$ with fitted coefficients $C\_{1}= 5.5$ and $C\_{2}= 11.6$ .

Modeling the Electronic Landscape: A Theoretical Framework

The S-Matrix formalism, when applied to scanning tunneling microscopy (STM), utilizes Nambu Non-equilibrium Green’s Functions (NEGF) to calculate tunneling conductance as a transmission probability. This approach treats the STM junction as a scattering problem, where electrons are incident from the tip, scatter at the junction, and are either transmitted or reflected. NEGF allows for the treatment of non-equilibrium conditions inherent in STM, where the tip and sample are not necessarily at the same Fermi level. The tunneling conductance, $G$ , is then directly proportional to the transmission coefficient, $T(E)$ , evaluated at the Fermi level, and is expressed as $G \propto T(E)$ . The formalism rigorously accounts for both incoming and outgoing electron waves, as well as the effects of correlations and many-body interactions within the system, providing a foundational method for interpreting STM data.

Combining the S-Matrix Formalism with a Tight Binding Model enables accurate representation of the electronic structure inherent to Scanning Tunneling Microscopy (STM) substrates. The Tight Binding Model simplifies the Hamiltonian by representing atomic orbitals and their interactions, allowing for computationally tractable calculations of energy bands and density of states. When integrated with the S-Matrix approach – which describes the probability of electron transmission – this combination accurately models the coupling between the STM tip and the sample surface. Specifically, it provides a means to calculate the tunneling matrix element, $V_{ij}$ , which defines the strength of interaction between tip and sample electronic states, and ultimately determines the tunneling current. This framework allows for precise prediction and interpretation of STM data, including local density of states measurements and differential conductance spectra.

The presence of multiple Fermi surfaces significantly complicates the analysis of tunneling phenomena, necessitating the use of a Two-Fermi-Surface Hamiltonian to accurately describe the system. This Hamiltonian accounts for the contributions of each Fermi surface to the total tunneling conductance, treating them as independent electron reservoirs. The total density of states is then a sum of the contributions from each surface, and the tunneling matrix elements must be considered for each contributing state. Systems exhibiting this behavior commonly arise in materials with complex band structures, such as those containing multiple partially filled bands, or in systems exhibiting topological phases of matter where band crossings lead to the formation of additional Fermi surfaces. Ignoring these multiple contributions can lead to substantial inaccuracies in the calculated tunneling current and misinterpretation of spectroscopic data.

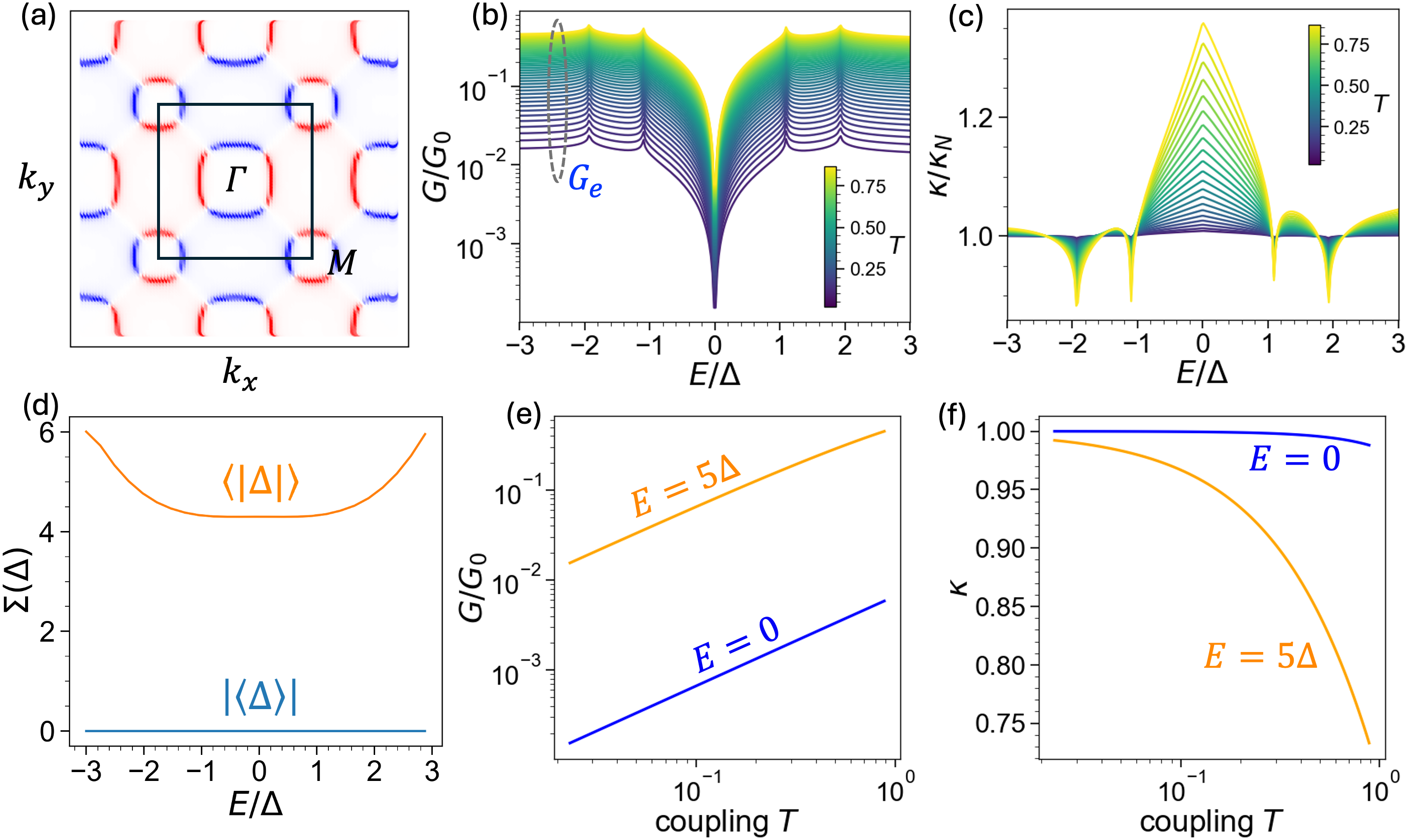
Calculations of the electronic structure and tunneling conductance reveal that a d-wave superconducting order parameter results in a finite average superconducting gap despite a zero expectation value for the gap function across the Brillouin zone, and that mid-gap conductance saturates slightly slower than outside the gap as tip-substrate coupling increases, as evidenced by spectroscopy of κ and <span class="katex-eq" data-katex-display="false">\kappa/ \kappa_{N}</span>. — Calculations of the electronic structure and tunneling conductance reveal that a d-wave superconducting order parameter results in a finite average superconducting gap despite a zero expectation value for the gap function across the Brillouin zone, and that mid-gap conductance saturates slightly slower than outside the gap as tip-substrate coupling increases, as evidenced by spectroscopy of κ and $\kappa/ \kappa_{N}$ .

Unveiling the Nuances of Unconventional Superconductivity

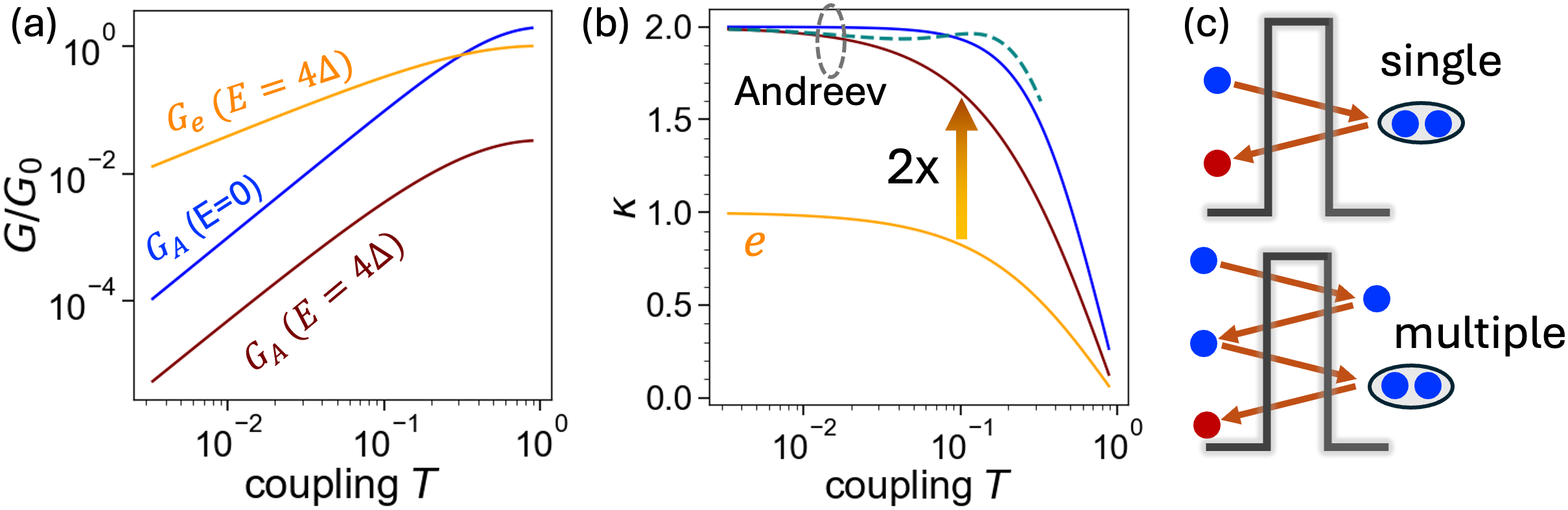
The ability to separate and analyze individual components within a tunneling signal hinges on the principle of additive decay rates. This characteristic proves invaluable when investigating complex superconducting systems, where multiple factors contribute to the overall observed behavior. By dissecting the signal’s decay, researchers can effectively isolate the contributions from various mechanisms – such as different superconducting orders or the presence of impurities – that would otherwise be indistinguishable. This decomposition isn’t merely a mathematical exercise; it provides a pathway to understanding the interplay of these factors and, crucially, to accurately determine the symmetry of the superconducting order parameter. The method allows for precise characterization, even in scenarios where conventional techniques struggle due to signal overlap, ultimately enhancing the ability to explore the nuanced properties of unconventional superconductors.

Distinguishing between different superconducting states relies heavily on the detailed structure of the energy gap, and recent advancements enable precise differentiation between conventional s-wave, anisotropic d-wave, and spatially modulated s± superconductors. A key metric in this determination is the ratio $\kappa/\kappa_N$ , representing the ratio of conductance within the superconducting gap to that outside. Observations consistently reveal that s-wave superconductors exhibit a significantly enhanced conductance ratio, with $\kappa/\kappa_N ≥ 2$ within the gap, signifying robust Andreev reflection. Conversely, d-wave symmetry demonstrates a suppressed conductance ratio of approximately 1, indicating weaker reflection. S± symmetry presents an intermediate behavior, yielding a ratio between 1 and 1.5, a value sensitive to both energy and the coupling strength between superconducting regions; this nuanced variation provides a powerful tool for characterizing these complex materials and unlocking their potential.

The nuanced characteristics of unconventional superconductivity are revealed through analysis of the ratio $\kappa/\kappa_N$ , which quantifies Andreev reflection. In d-wave superconductors, this ratio consistently approaches unity, signifying a marked suppression of Andreev reflection – a process where an electron and a hole are created at an interface. Conversely, s± superconductors exhibit a more variable response, with $\kappa/\kappa_N$ values falling between 1 and 1.5; this range is not fixed but dynamically adjusts based on the energy of the electrons involved and the strength of the coupling between the superconducting regions. This sensitivity provides a diagnostic tool, allowing researchers to differentiate between these complex superconducting states and map their underlying electronic properties, showcasing how subtle variations in symmetry lead to measurable differences in electron behavior.

The nuances of electron transport in unconventional superconductors become readily apparent when measurements exceed a conductance threshold of 0.1 $G_0$ , where $G_0$ represents the quantum of conductance. Below this level, the simplistic picture of Andreev reflection and tunneling dominates; however, surpassing it reveals a more complex interplay of higher-order processes. These effects, stemming from multiple Andreev reflections and enhanced tunneling probabilities, significantly alter the observed spectra and introduce deviations from the expected behavior in single-particle tunneling models. Consequently, accurate characterization of the superconducting gap structure and symmetry requires careful consideration of these non-linear phenomena, as they introduce subtle but crucial signatures distinguishing between different superconducting states and providing a deeper understanding of the underlying physics.

Simulations of a weakly to intermediately coupled s-wave superconductor reveal that quasiparticle tunneling and Andreev reflection processes, characterized by conductance spectroscopy and scaling with normal conductance, exhibit a coupling-dependent excess decay rate κ reconstructable from conductance data and partitionable into tunneling and Andreev reflection contributions.

The research presented challenges conventional assumptions about characterizing superconducting materials. It posits a method-disentangling Andreev and quasiparticle currents-that actively tests the boundaries of current spectroscopic techniques. This mirrors a core tenet of scientific inquiry: understanding arises from controlled disruption. As Isaac Newton observed, “I do not know what I may seem to the world, but to myself I seem to be a boy playing on the seashore.” The study, like Newton’s playful exploration, meticulously examines the ‘shoreline’ of superconducting behavior, breaking down complex currents to reveal underlying principles and ultimately, a clearer picture of pairing symmetry and the electronic structure of unconventional superconductors. The careful manipulation of tunnel junctions and analysis of the κ/κN ratio isn’t about confirming expectations, but about discovering what happens when those expectations are subtly, systematically, broken.

Beyond the Tunnel

The exploitation of Andreev reflection as a probe of superconducting symmetry offers an intriguing, if predictable, path forward. This work, by meticulously dissecting the decay of tunneling currents, provides a refined exploit of comprehension-a means of reverse-engineering the electronic structure hidden within unconventional superconductors. However, the additive nature of the currents, while convenient for analysis, feels… constrained. It suggests an underlying assumption about the system’s simplicity that may not hold universally. The real challenge lies not in refining the measurement of κ/κN, but in confronting the scenarios where this neat dissection fails.

Future investigations should deliberately seek out complexity. Heterostructures, disordered materials, or systems driven far from equilibrium will undoubtedly expose the limitations of this approach. Can the principles demonstrated here be extended to disentangle multiple coexisting superconducting orders? Or will the inherent ambiguities of tunneling spectroscopy ultimately demand a more holistic, less reductionist methodology? The answer, predictably, will likely reside in the noise-in the signals currently dismissed as artifacts.

The true test won’t be to confirm existing theories, but to engineer a system that breaks the model. To find the configuration where Andreev reflection yields not clarity, but delightful, instructive contradiction. Only then will the full potential of this technique be revealed, and the underlying rules of superconducting pairing truly challenged.

Original article: https://arxiv.org/pdf/2601.20798.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/

Deconstructing Superconductivity: Peeling Back the Layers

Tunneling Andreev Reflection: A New Lens on Electronic Behavior

Modeling the Electronic Landscape: A Theoretical Framework

Unveiling the Nuances of Unconventional Superconductivity

Beyond the Tunnel

See also: