Author: Denis Avetisyan
A new analysis explores how coarse-graining techniques can bridge the gap between theoretical predictions of black hole evaporation and the fundamental principles of quantum mechanics.

This review examines the challenges of maintaining unitarity in the semiclassical description of Hawking radiation through the lens of AdS/CFT correspondence and ensemble averaging.
The apparent conflict between quantum mechanics’ unitarity and the thermal nature of Hawking radiation remains a central puzzle in theoretical physics. This is addressed in ‘A Reverse Black Hole Information Problem’, which investigates how semiclassical black hole evaporation can emerge from the underlying unitary dynamics of a boundary conformal field theory. By constructing colliding wavepacket states in AdS/CFT and exploring various coarse-graining prescriptions, we demonstrate a pathway connecting exact boundary states to mixed states consistent with Hawking radiation and the expected purity loss. Does this approach offer a resolution to the information paradox by revealing how ensemble averaging reconciles quantum mechanics with observed black hole behavior?
The Allure of Lost Information: A Quantum Enigma
The seemingly straightforward process of black hole evaporation, predicted by Stephen Hawking, presents a profound challenge to the foundations of quantum mechanics through what is known as the Information Problem. Quantum mechanics dictates that information – essentially, the complete description of a physical system – must always be conserved; its evolution should be unitary, meaning reversible. However, Hawking’s calculations suggest that as a black hole evaporates via Hawking radiation, this radiation is thermal – a random distribution of particles – and carries no information about what originally fell into the black hole. This implies that information is effectively destroyed, violating the principle of unitary dynamics and creating a paradox: either quantum mechanics breaks down in the presence of strong gravity, or our understanding of black hole evaporation is incomplete. The loss of information would be akin to burning a book and claiming all knowledge within it is simply gone, an unacceptable outcome for a fundamental law of physics. This has motivated decades of research attempting to reconcile gravity with quantum mechanics and pinpoint where – or if – information is actually preserved during black hole evaporation.
The apparent loss of information within black holes directly confronts the principle of unitary dynamics, a fundamental tenet of quantum mechanics. Unitary dynamics dictates that quantum evolution should be reversible – meaning, in theory, one should always be able to trace a system’s current state back to its past. However, if information truly vanishes within a black hole as Hawking radiation suggests, this reversibility is broken, violating unitarity. This isn’t merely a technical detail; unitarity is deeply connected to the conservation of probability in quantum theory, and its failure would necessitate a substantial revision of established quantum principles. The challenge lies in reconciling the seemingly inevitable information loss with the rigorous mathematical framework that underpins all successful quantum predictions, prompting physicists to explore radical ideas about the nature of spacetime and quantum gravity to preserve this cornerstone of modern physics.
Semiclassical Anti-de Sitter (AdS) gravity offers a unique theoretical arena for investigating the black hole information paradox by proposing a duality between gravity and quantum mechanics. This framework posits that a theory of gravity in a higher-dimensional AdS space is mathematically equivalent to a quantum field theory residing on the boundary of that space – a lower-dimensional construct without gravity. This correspondence, often described as a holographic projection, allows physicists to study phenomena difficult to analyze directly within quantum gravity, like black hole evaporation, by translating them into calculations within the more manageable quantum field theory. Essentially, all the information that falls into a black hole is not lost, but rather encoded on its boundary, similar to how a hologram stores a three-dimensional image on a two-dimensional surface; this offers a potential resolution to the paradox, suggesting information is preserved, albeit in a scrambled form, and avoids violations of Unitary Dynamics.

Entanglement as a Signature of Spacetime Geometry
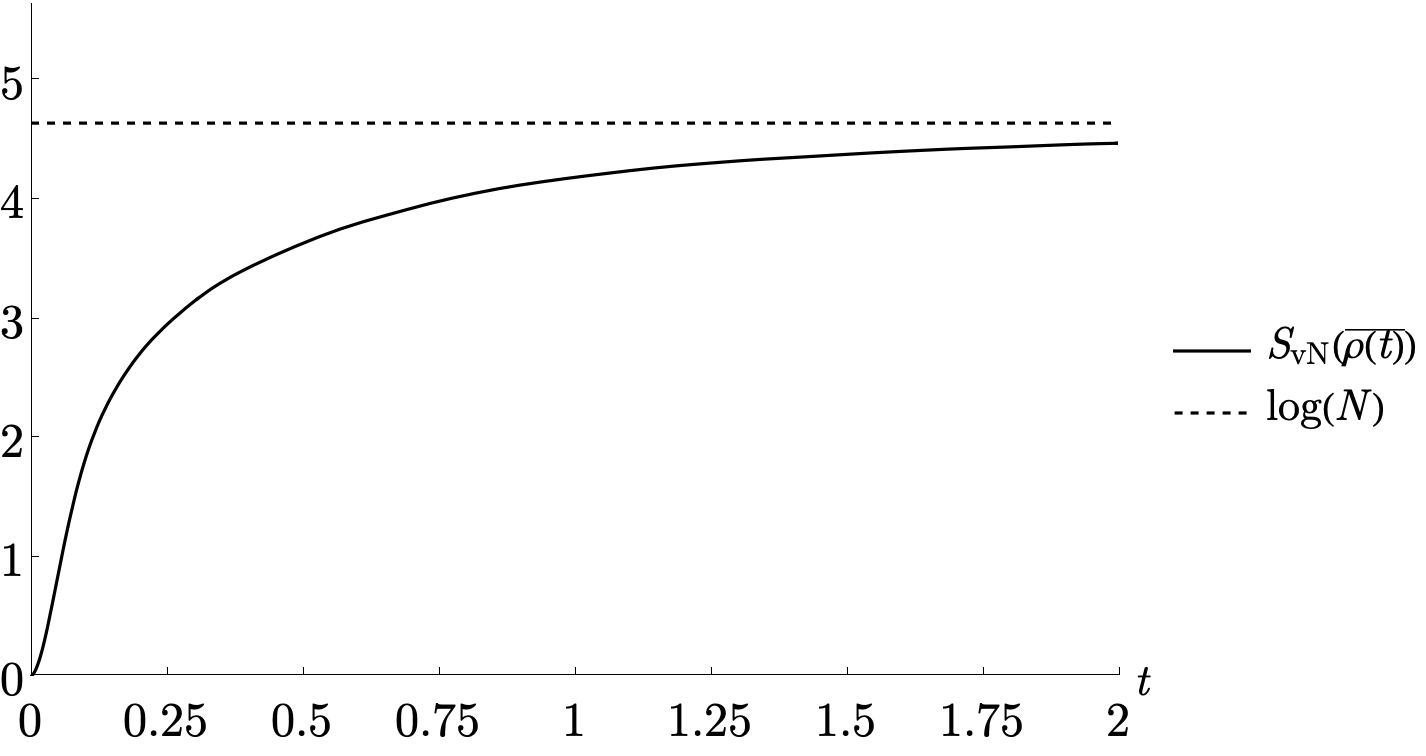
Von Neumann entropy, denoted as S(ρ) = -Tr(ρlog_2ρ), serves as a quantifiable measure of entanglement within a quantum system described by the density matrix ρ. In the context of spacetime, this metric is critical because it directly relates to the degrees of freedom encoding information. Specifically, the entanglement entropy calculated from a region’s boundary is proportional to the area of that boundary, as formalized by the Ryu-Takayanagi formula and its generalizations. This area law suggests that information about the bulk spacetime is encoded on its lower-dimensional boundary, and the Von Neumann entropy quantifies the amount of that information. Consequently, understanding the evolution of Von Neumann entropy is central to resolving the information paradox associated with black holes and characterizing the emergence of spacetime geometry from underlying quantum states.
Coarse-graining is an essential technique for applying Semiclassical AdS/CFT correspondence to complex quantum systems. This process involves reducing the degrees of freedom considered in a system by focusing on macroscopic, low-energy properties while effectively integrating out high-frequency modes. Recent research demonstrates a direct relationship between specific coarse-graining procedures and the emergence of semiclassical gravity in Anti-de Sitter (AdS) space. Specifically, the methodology used to simplify the quantum system impacts the resulting gravitational description; properly implemented coarse-graining protocols are necessary to recover the expected semiclassical behavior, avoiding divergences and ensuring a consistent connection between the boundary quantum field theory and the bulk gravitational theory. This linkage allows for the study of quantum gravity effects through the analysis of simplified, effectively classical systems.
The purity of a coarse-grained quantum state, mathematically represented by Tr(\bar{\rho}^2), serves as a quantifiable metric for assessing information preservation during black hole formation. Research demonstrates a direct correlation between the initial purity of the quantum state and the purity of its coarse-grained approximation; specifically, decreases in coarse-grained purity occur on a timescale consistent with the formation of the event horizon. This temporal alignment suggests that monitoring changes in Tr(\bar{\rho}^2) provides a potential mechanism for tracking information as it transitions from being encoded in the initial state to being potentially retained within the coarse-grained approximation, thereby offering a pathway to address the black hole information paradox.
The Holographic Dictionary: Mapping Boundaries to Bulk
The Anti-de Sitter (AdS)/Conformal Field Theory (CFT) correspondence posits a duality between gravitational theories in the AdS bulk and quantum mechanics in a lower-dimensional one. This boundary CFT effectively “encodes” all information about the higher-dimensional gravitational physics; specifically, local operators in the CFT correspond to gravitational degrees of freedom in the bulk. Correlation functions of these boundary operators, which describe the probabilistic relationships between them, directly map to dynamical processes and geometric features within the AdS space. Therefore, analyzing the correlations between operators in the boundary CFT provides a non-perturbative method for investigating the gravitational dynamics of the corresponding AdS spacetime, offering insights into phenomena like black hole formation and Hawking radiation.
Two-point correlation functions in Boundary CFTs quantify the probability of simultaneously observing two operators at separated points, providing critical information about the underlying theory’s structure and the behavior of matter. Analysis of these functions reveals details regarding operator scaling dimensions and the propagation of excitations. Specifically, the behavior of two-point functions can indicate phase transitions, such as those between confined and deconfined states of matter; a change in the power-law decay of the correlation function often signals a shift in the system’s fundamental degrees of freedom. The precise form of these functions, including oscillatory behavior and the presence of poles, directly relates to the mass spectrum and interactions of particles within the dual gravitational theory.
Operator Product Expansion (OPE) coefficients directly encode information about the gravitational dynamics of the dual AdS spacetime. These coefficients characterize the singularities of operator correlations as spatial separation approaches zero and determine the allowed interactions within the Boundary Conformal Field Theory (CFT). Critically, the timescale for the mixing of states within the CFT, and therefore the rate of information scrambling, is governed by parameters such as σ – related to the Lyapunov exponent – and the dimensionality of the Hilbert subspaces ℋ(n). Calculations demonstrate that these parameters yield timescales consistent with expectations from the bulk theory concerning black hole evaporation and the restoration of unitarity, suggesting a precise mapping between CFT state mixing and gravitational dynamics.
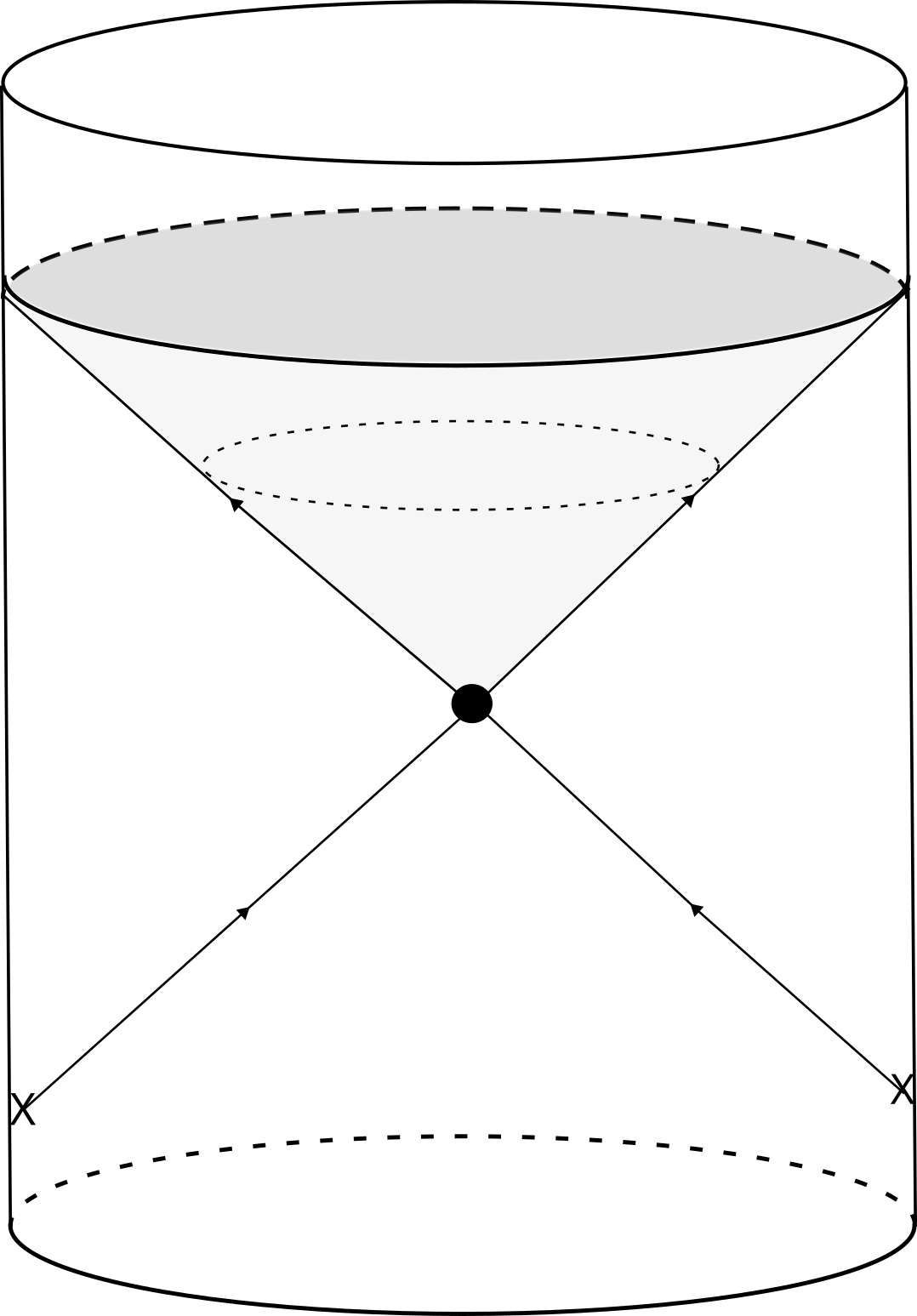
Wormholes and Entanglement: A Topological Resolution?
The preservation of quantum entanglement – a cornerstone of quantum mechanics – faces unique challenges when considering systems with multiple boundaries, such as those arising in the study of black holes and spacetime. Theoretical physicists hypothesize that multiboundary wormholes, topological features connecting disparate regions of spacetime, may provide a crucial mechanism for maintaining these fragile quantum correlations. These wormholes aren’t merely theoretical curiosities; they emerge naturally in calculations involving AdS/CFT correspondence, a powerful duality relating gravity in higher dimensions to quantum field theories on lower-dimensional boundaries. The geometry of these wormholes suggests a pathway for information to traverse and reconnect, effectively shielding entanglement from decoherence that would otherwise occur due to the complex interplay of multiple boundaries. Investigating these connections is paramount to resolving the ‘factorization puzzle’ and ultimately understanding how information is encoded and preserved in the quantum fabric of spacetime itself.
The behavior of correlation functions in systems with multiple boundaries presents a significant challenge known as the Factorization Puzzle. Typically, correlation functions are expected to factorize – meaning the influence between distant regions is negligible – but this expectation breaks down when boundaries are introduced in a holographic context. This non-factorization suggests that the boundaries are not merely passive endpoints of spacetime, but actively participate in the system’s quantum entanglement. Resolving this puzzle requires a refined understanding of how entanglement is distributed and preserved across these boundaries, pushing the limits of holographic entanglement calculations and demanding new theoretical frameworks to describe the interplay between boundary and bulk geometries. The complexity arises because each additional boundary introduces further connections and correlations, making it increasingly difficult to predict and accurately calculate the system’s behavior – a problem central to understanding the nature of quantum gravity and information preservation in black holes.
Calculations of entanglement entropy often reveal the presence of replica wormholes – hypothetical tunnels through spacetime – offering a potential resolution to the factorization puzzle concerning correlated boundaries in holographic systems. These wormholes arise as mathematical constructs when attempting to quantify how entanglement is distributed across multiple boundaries, suggesting a deep connection between geometry and quantum information. To probe this relationship, researchers employ the spectral form factor, expressed as g(t) = |Tr(PH e^(iHt))/Tr(PH)|², which measures the level of chaoticity within the system. By analyzing how quickly this form factor decays, scientists aim to establish a quantifiable link between the behavior of entanglement on the boundary of spacetime and the geometry of the wormholes in the bulk, ultimately shedding light on how information is preserved even in the presence of strong gravitational effects and complex quantum interactions.
Towards a Complete Theory: Coarse-Graining and the Search for Universal Principles
Holographic duality, a cornerstone of theoretical physics, proposes a connection between gravity in a higher-dimensional space and quantum mechanics in a lower-dimensional one, but calculations within this framework often encounter significant ambiguities. Ensemble averaged theories provide a powerful strategy to navigate these complexities by moving beyond considering a single, specific quantum gravity theory and instead averaging over a vast ensemble of possibilities. This approach, while seemingly radical, allows physicists to simplify calculations and obtain robust results that are less sensitive to the details of any particular theory. By assuming, guided by the Maximum Ignorance Principle, that each possible theory within the ensemble is equally probable, researchers can effectively “smooth out” the ambiguities and extract universal features of the holographic duality, bringing them closer to resolving long-standing puzzles like the black hole information paradox and gaining deeper insights into the fundamental nature of spacetime.
The construction of theoretical ensembles in holographic duality relies heavily on the Maximum Ignorance Principle, a guiding philosophy that champions simplicity by assigning equal probability to all permissible theoretical possibilities. This isn’t merely a mathematical convenience; it represents a deliberate avoidance of prejudice, refusing to favor any specific background or solution over another without compelling evidence. By embracing this principle, physicists create a diverse ‘landscape’ of theoretical models, effectively averaging over them to arrive at robust, universal predictions. The resulting ensemble acts as a smoothing mechanism, diminishing the impact of individual, potentially spurious, features present in any single theory and revealing underlying principles applicable across a broad range of gravitational scenarios. This approach provides a powerful tool for navigating the complexities of quantum gravity and tackling long-standing problems like the black hole information paradox, offering a pathway towards a more complete understanding of spacetime and its quantum nature.
Current research suggests a powerful connection between the behavior of integrable and chaotic systems and the efficacy of coarse-graining techniques used in holographic duality. Coarse-graining, essential for bridging the gap between microscopic quantum gravity and macroscopic observations, attempts to simplify complex systems by focusing on large-scale properties. However, the effectiveness of these techniques appears deeply influenced by whether the underlying system exhibits integrable – predictable and non-chaotic – or chaotic dynamics. Studies indicate that chaotic systems require significantly more sophisticated coarse-graining approaches to accurately capture their essential features, potentially explaining why the information paradox – the apparent loss of information in black holes – remains a challenge. Understanding how these differing dynamics impact entanglement structure, a key component of holographic duality, may reveal how information is subtly preserved even within the extreme gravitational environment of a black hole, ultimately offering a path towards resolving this long-standing paradox and deepening the understanding of quantum gravity.
The pursuit of resolving the black hole information paradox, as detailed in this exploration of coarse-graining maps and ensemble averaging, echoes a fundamental quest for order within apparent chaos. It’s a process of discerning underlying structure, a refinement of perspective. Søren Kierkegaard observed, “Life can only be understood backwards; but it must be lived forwards.” This resonates with the paper’s approach – attempting to understand the ‘forward’ evolution of Hawking radiation by reconstructing the ‘backward’ state of the black hole interior. The elegance lies in seeking a consistent narrative, a harmonious relationship between quantum mechanics and general relativity, even when faced with the complexities of quantum chaos and the need for approximations like the microcanonical ensemble.
The Horizon Beckons
The pursuit of a resolution to the information paradox, as explored through coarse-graining maps and ensemble averaging, reveals not a single chasm to bridge, but a landscape of subtle distinctions. The elegance of a unitary theory demands a certain austerity, yet the observed universe appears stubbornly resistant to such neatness. This work suggests that the devil resides not in the loss of information itself, but in the approximations-the choices made in connecting the microscopic, pristine quantum state to the messy, thermalized reality of Hawking radiation. A truly satisfying answer will likely necessitate a deeper understanding of how quantum chaos manifests at the boundary of spacetime, and how this chaos influences the emergent geometry itself.
Future investigations should perhaps focus less on recovering information, and more on defining precisely what constitutes “information” within the context of a gravitational system. The microcanonical ensemble, while theoretically appealing, remains a difficult beast to tame, and its connection to the more accessible canonical ensemble warrants further scrutiny. A more refined mapping between these ensembles-one that respects both unitarity and the semiclassical description-could illuminate the precise mechanism by which information is encoded and preserved.
Ultimately, the enduring challenge lies in reconciling the abstract beauty of quantum mechanics with the brute physicality of gravity. The horizon, it seems, is not a barrier to information, but a mirror reflecting the limits of current understanding. The path forward demands not just mathematical ingenuity, but a willingness to question fundamental assumptions about the nature of spacetime and the very meaning of observation.
Original article: https://arxiv.org/pdf/2601.22077.pdf
Contact the author: https://www.linkedin.com/in/avetisyan/
See also:
- Best Controller Settings for ARC Raiders
- Ashes of Creation Rogue Guide for Beginners
- Stephen Colbert Jokes This Could Be Next Job After Late Show Canceled
- Is XRP ETF the New Stock Market Rockstar? Find Out Why Everyone’s Obsessed!
- 7 Home Alone Moments That Still Make No Sense (And #2 Is a Plot Hole)
- 10 X-Men Batman Could Beat (Ranked By How Hard It’d Be)
- Neverness to Everness ‘Co-Ex Test’ sign-ups now available
- Best Werewolf Movies (October 2025)
- DCU Nightwing Contender Addresses Casting Rumors & Reveals His Other Dream DC Role [Exclusive]
- 10 Great Netflix Dramas That Nobody Talks About
2026-01-30 11:10