Author: Denis Avetisyan
New research reveals a surprisingly ordered structure within black holes, challenging traditional models of their final moments.
Higher-derivative gravity modifies the near-singularity dynamics, leading to periodic oscillations and potentially finite-volume singularities beyond the Kasner epoch.
The prevailing picture of black hole interiors, based on oscillating Kasner epochs near the singularity, breaks down when quantum gravitational effects become significant. This is the central argument of ‘Beyond Kasner Epochs: Ordered Oscillations and Spike Dynamics Inside Black Holes with Higher-Derivative Corrections’, which investigates the impact of higher-derivative corrections on the dynamics within black holes. Our analysis reveals a richer phase space beyond the classical BKL conjecture, characterized by modified Kasner eras, sustained periodic oscillations, and-remarkably-oscillatory spike dynamics exhibiting growing amplitude. Do these findings suggest a pathway towards resolving the singularity problem and understanding the ultimate fate of information in these extreme gravitational environments?
The Inevitable Breakdown: Where Gravity Loses Its Grip
General Relativity, Einstein’s celebrated theory of gravity, while remarkably successful in describing the universe on large scales, contains within it the seeds of its own potential failure. The theory predicts the formation of spacetime singularities – points where gravitational forces become infinitely strong, and the curvature of spacetime becomes infinite. These aren’t simply regions of extreme gravity; they represent a breakdown of the mathematical framework itself, rendering the equations of General Relativity useless for describing what happens at or beyond these points. Such singularities are predicted to exist within black holes, at the very beginning of the universe in the Big Bang, and potentially in other exotic cosmological scenarios. This poses a fundamental theoretical challenge: a complete and consistent theory of gravity should be able to describe the behavior of spacetime under all conditions, including those where General Relativity fails. The existence of singularities therefore signals the need for a more comprehensive theory – one that could potentially incorporate quantum mechanics to resolve these problematic points and provide a complete picture of gravity at its most extreme.
The BKL conjecture proposes that as spacetime approaches a singularity – a point where the laws of physics as currently understood break down – its behavior doesn’t simply collapse into a static point, but rather enters a highly chaotic regime characterized by rapidly oscillating gravitational fields. This isn’t a smooth descent into nothingness, but a turbulent cascade of gravitational waves bouncing around and amplifying each other. However, rigorously demonstrating the validity of this conjecture proves exceptionally difficult because it demands a detailed understanding of gravity in the “strong-field regime” – situations where gravitational forces are incredibly intense, far beyond anything observable in the relatively weak gravitational fields of everyday experience or even most astronomical phenomena. Proving the BKL conjecture therefore necessitates developing and applying mathematical tools capable of accurately describing spacetime dynamics under these extreme conditions, a key stepping stone towards a more complete theory reconciling general relativity with quantum mechanics.
The quest for a complete theory of quantum gravity fundamentally hinges on resolving the mysteries surrounding spacetime singularities. These points, predicted by classical General Relativity where gravitational forces become infinite and the laws of physics as currently understood cease to apply, represent a critical breakdown in predictability. A successful theory must not merely acknowledge these singularities, but explain what happens at them – does spacetime simply end, or is there a more nuanced, potentially quantum, structure revealed? Understanding the behavior of spacetime under such extreme conditions is not simply an academic exercise; it’s a necessary step to reconcile General Relativity with quantum mechanics. Current theoretical frameworks, like string theory and loop quantum gravity, propose different resolutions, often suggesting that spacetime itself is quantized or that singularities are smoothed out by quantum effects. However, verifying these proposals demands a deeper understanding of the physics at the singularity – a region where classical descriptions are inherently inadequate and new, quantum descriptions are required to paint a complete picture of reality.
Patching the Cracks: Beyond Einstein’s Framework
Higher-derivative corrections to the Einstein-Hilbert action represent a theoretical approach to address the issue of singularities in general relativity. The standard Einstein-Hilbert action, when used to describe gravity, predicts the formation of singularities – points where spacetime curvature becomes infinite – within black holes and at the Big Bang. Introducing higher-order curvature terms, such as R^2 or R_{\mu\nu}R^{\mu\nu}, modifies the gravitational dynamics and effectively softens the extreme curvature near these singularities. This smoothing effect arises because the higher-derivative terms contribute to the energy-momentum tensor, altering the gravitational field equations and preventing the curvature from reaching infinity. While these corrections introduce complexities to the theory, they provide a potential mechanism for obtaining a more complete and physically realistic description of gravity in strong-field regimes.
Lovelock gravity represents a systematic extension to general relativity that allows for the inclusion of higher-order curvature terms in the gravitational action without introducing problematic ghost instabilities. Standard modifications to the Einstein-Hilbert action involving higher derivatives typically lead to equations of motion with more than two time derivatives, resulting in instabilities and non-physical predictions. Lovelock’s theorem demonstrates that constructing a gravitational action with only second-order equations of motion – ensuring a well-defined initial value problem – is possible by considering specific combinations of curvature tensors. The most commonly studied example, Einstein-Gauss-Bonnet (EGB) gravity, incorporates a term proportional to the R^2 scalar curvature and its contractions, maintaining second-order equations of motion and providing a consistent framework for exploring modified gravity effects, particularly in strong gravitational regimes where singularities arise.
Einstein-Gauss-Bonnet (EGB) gravity represents a specific, analytically manageable extension of general relativity within the broader Lovelock framework. It modifies the gravitational action by adding terms involving the R_{μνρσ} Riemann tensor and its contractions, allowing for corrections to the Einstein field equations while crucially preserving second-order equations of motion. This characteristic avoids the introduction of problematic ghost instabilities often associated with higher-derivative gravity theories. Consequently, Einstein-GB gravity serves as a valuable testbed for investigating how modifications to general relativity can influence the formation and nature of singularities, particularly in black hole and cosmological scenarios, offering a pathway to explore potential resolutions to these problematic points in spacetime.
Peering into the Abyss: Probing Dynamics with Modified Gravity
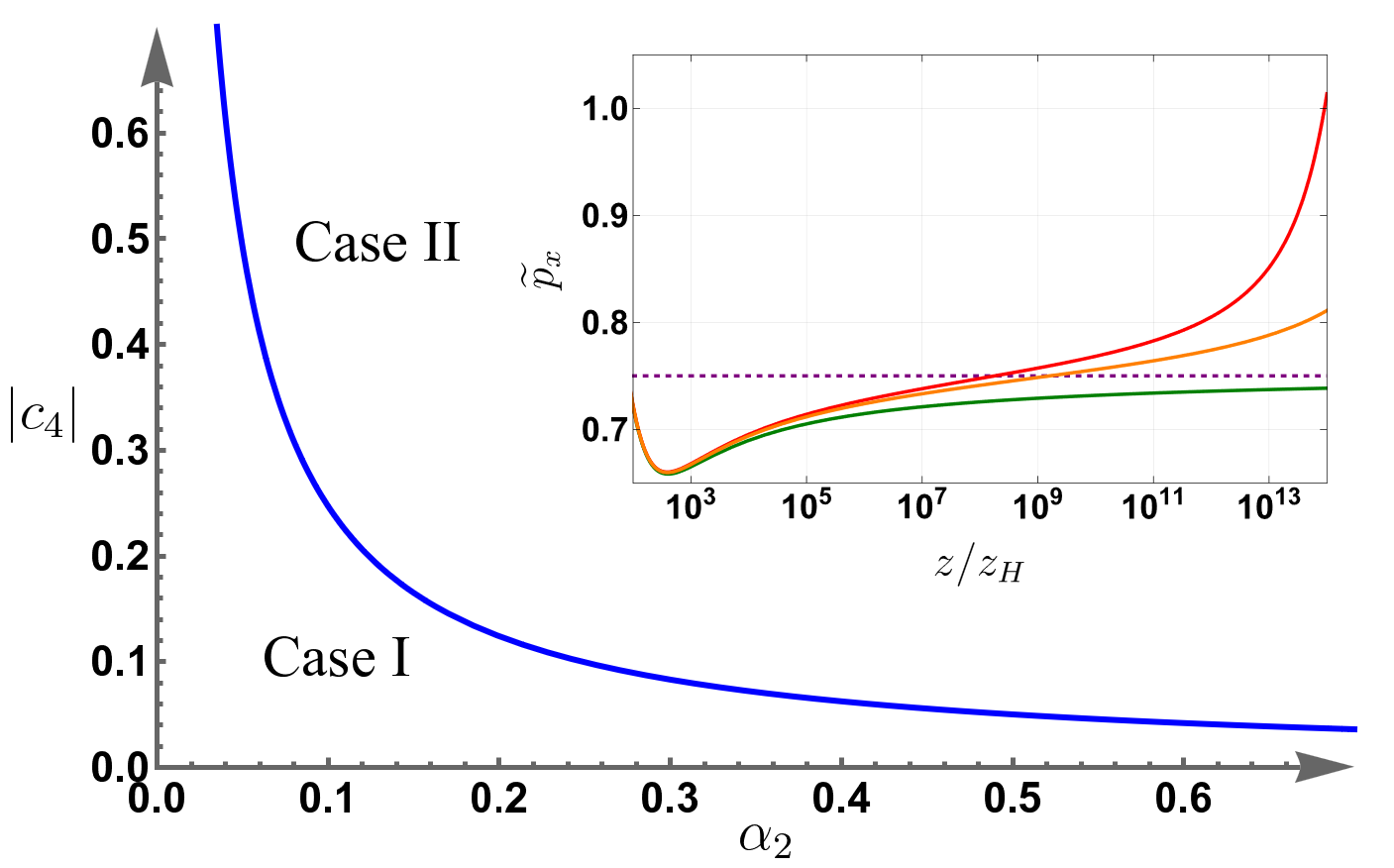
Analysis of the Kasner exponent within the framework of Einstein-Gauss-Bonnet (EGB) gravity demonstrates alterations to the singularity structure when contrasted with General Relativity (GR). In GR, the Kasner metric describes the approach to a singularity with anisotropic spatial expansion or contraction. However, the inclusion of the Gauss-Bonnet term, a higher-order curvature correction to the Einstein-Hilbert action, modifies the effective gravitational dynamics. This modification results in a shift in the allowed Kasner exponents, influencing the rates of anisotropic expansion or contraction near the singularity. Specifically, EGB gravity can alleviate the strong singularity present in GR by introducing corrections to the geodesic equation, potentially leading to a weaker or even regular singularity, depending on the specific parameters of the EGB theory. The modified Kasner exponents reflect these changes in the spacetime geometry near the singularity.
The coupling of a ScalarField to Einstein-Gauss-Bonnet (EGB) Gravity introduces the potential for “Hairy Black Holes,” which possess non-trivial scalar hair beyond the no-hair theorem of General Relativity. This arises because the scalar field is not necessarily constant on the black hole horizon, leading to modifications of the spacetime geometry and gravitational dynamics. Specifically, the scalar field contributes an additional source term to the field equations, altering the black hole’s mass and angular momentum parameters as observed at infinity. This coupling also influences the black hole’s event horizon and ergosphere, potentially leading to distinct observational signatures compared to Kerr black holes predicted by classical General Relativity. The effective gravitational dynamics are therefore modified, impacting both the near-horizon and far-field behavior of the spacetime.
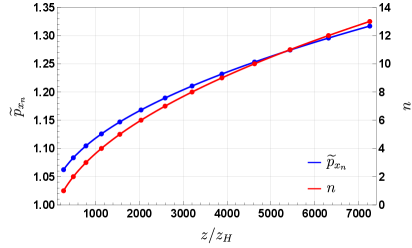
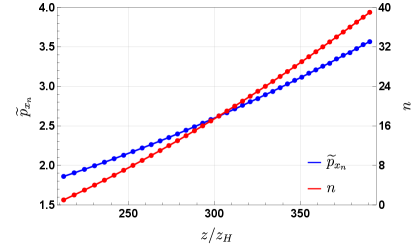
Effective action techniques, when applied to the spacetime near the singularity, provide an approximation of the dynamics and reveal specific scaling relationships. Analysis indicates that the oscillation period exhibits logarithmic scaling, described by the equation log(z/z_H) = 3.67 + 5.02n, where ‘n’ represents the oscillation number and z_H is a reference scale. Furthermore, the positions of the observed spikes demonstrate a power-law dependence on ‘n’, characterized by the formula z_n = 3.89(n+0.64)^{1/0.78}. This power-law relationship yields a scaling exponent of 0.78, providing a quantitative measure of how the spike positions change with increasing oscillation number.
The Long View: Implications for Spacetime and Future Research
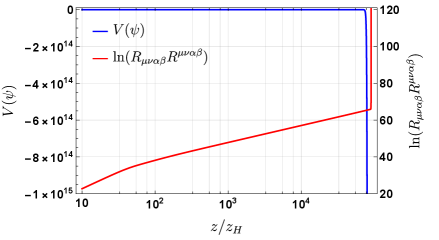
Investigations into modified gravity theories reveal a potential pathway to resolving problematic predictions of classical general relativity concerning singularities. The inclusion of higher-order curvature terms, such as the Gauss-Bonnet (GB) term, alters the gravitational dynamics in extreme conditions, allowing for the formation of finite-volume singularities where the spacetime curvature remains bounded despite the concentration of matter. Recent studies confirm that while unbounded scalar potentials still inevitably lead to curvature singularities, these singularities occur within a finite spatial volume – a significant departure from the infinite-volume singularities predicted by standard models. This finding suggests that modifications to Einstein’s theory, by introducing terms like the GBTerm, may offer a crucial mechanism for avoiding the breakdown of predictability at the heart of black holes and the very early universe, potentially paving the way for a more complete theory that unifies gravity with quantum mechanics.
The peculiar oscillatory behavior observed in Kasner exponents, termed SpikeDynamics, offers a compelling window into the nature of singularities within modified gravity theories. These exponents, which dictate the rates of expansion along different spatial directions, typically exhibit stable, predictable values near a singularity. However, the introduction of higher-order curvature terms, such as the Gauss-Bonnet term, disrupts this stability, causing the exponents to oscillate wildly. This phenomenon isn’t merely a mathematical artifact; it suggests that the strong gravitational regime fundamentally alters the dynamics near the singularity, preventing the formation of a traditional, infinitely dense point. Instead, the oscillatory dynamics imply a more complex, potentially finite-volume singularity where spacetime continues to evolve, albeit in a highly distorted manner, offering crucial clues to the development of a more complete theory of quantum gravity and the ultimate fate of spacetime itself.
Investigating the relationship between the Kretschmann scalar – a measure of spacetime curvature – and the emergence of finite-volume singularities represents a crucial step towards a more complete theory of quantum gravity. Current research suggests that modifications to general relativity, incorporating terms like the Gauss-Bonnet term, can avoid the traditional infinite density singularities predicted by classical physics, instead allowing for singularities contained within a finite region of spacetime. Analyzing how the Kretschmann scalar behaves as spacetime approaches these finite-volume singularities – specifically, identifying any predictive patterns or critical thresholds – may reveal fundamental clues about the underlying quantum nature of gravity. This line of inquiry offers the potential to connect geometrical properties of spacetime with quantum effects, potentially offering testable predictions and constraints for future theoretical models aiming to unify gravity with quantum mechanics. Understanding this connection could ultimately resolve long-standing issues related to the singularity problem and provide a deeper insight into the very fabric of spacetime at extreme densities.

The pursuit of elegance in theoretical physics often encounters the harsh realities of implementation. This paper, detailing the complex dynamics within black holes through higher-derivative gravity, exemplifies that tendency. It moves beyond the classically predicted billiard-like behavior near the singularity, revealing oscillations and spikes – phenomena unforeseen in simpler models. As Francis Bacon observed, “There is no pleasure in having done that which is easy.” The researchers didn’t settle for established paradigms; they actively sought complexity, only to uncover a universe of even more nuanced behaviors. The claim of finite-volume singularities, however, feels predictably optimistic. One suspects production – in this case, the universe itself – will find a way to introduce further complications, exceeding even these detailed calculations.
The Road Ahead
The exploration of black hole interiors, even with the added complexity of higher-derivative corrections, ultimately reveals a landscape of diminishing returns. This work identifies modified Kasner epochs and intriguing oscillatory behavior, but the persistence of singularities, even finite-volume ones, suggests a fundamental limit to how much can be ‘smoothed’ away with increasingly elaborate field theories. The spikes, the periodicities – these are details layered atop an inevitability. Tests, of course, are a form of faith, not certainty.
Future investigations will undoubtedly focus on quantifying the robustness of these findings. Will these ‘ordered oscillations’ survive the inevitable introduction of matter fields? Can these higher-derivative terms actually stabilize the singularity in a physically realistic scenario, or are they merely shifting the problem to a smaller, more inconvenient scale? One suspects the latter. The real challenge isn’t finding a way around the singularity, but understanding why the universe seems so insistent on creating them.
Ultimately, the continued refinement of these models may yield little more than a more detailed catalog of how things fail. And yet, there is a certain beauty in that. A system that doesn’t crash on Mondays is a rare and precious thing. The pursuit of these internal dynamics, even if destined to reveal more complexity than resolution, provides a valuable lesson: elegance is a fragile illusion, and production always finds a way.
Original article: https://arxiv.org/pdf/2601.21658.pdf
Contact the author: https://www.linkedin.com/in/avetisyan/
See also:
- Best Controller Settings for ARC Raiders
- Ashes of Creation Rogue Guide for Beginners
- Stephen Colbert Jokes This Could Be Next Job After Late Show Canceled
- Is XRP ETF the New Stock Market Rockstar? Find Out Why Everyone’s Obsessed!
- 7 Home Alone Moments That Still Make No Sense (And #2 Is a Plot Hole)
- 10 Great Netflix Dramas That Nobody Talks About
- All 6 Takopi’s Original Sin Episodes, Ranked
- Best Werewolf Movies (October 2025)
- DCU Nightwing Contender Addresses Casting Rumors & Reveals His Other Dream DC Role [Exclusive]
- Donkey Kong Country Returns HD version 1.1.0 update now available, adds Dixie Kong and Switch 2 enhancements
2026-01-30 20:35