Author: Denis Avetisyan
New research details the observation and characterization of an underdamped amplitude mode arising from quantum quenches in a one-dimensional spin system.
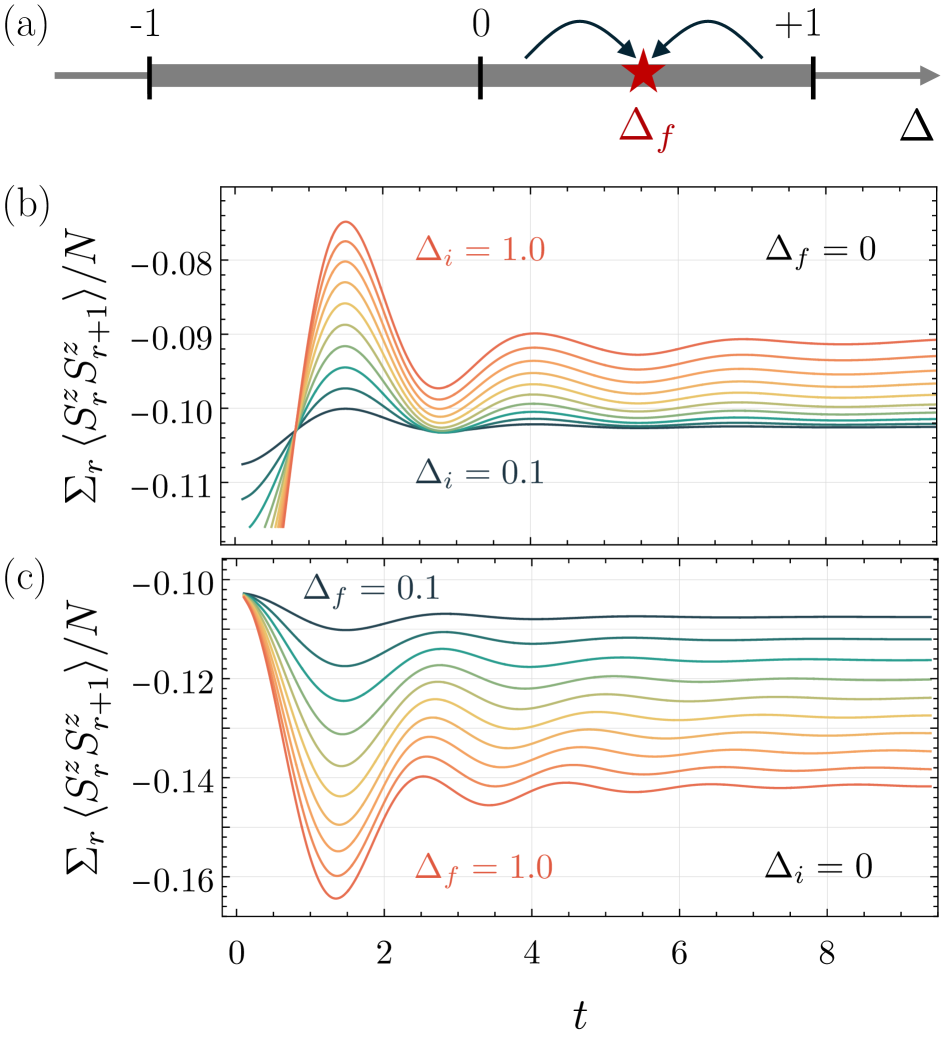
This study identifies and links an amplitude mode in the gapless phase of the XXZ model to string excitations within the Bethe ansatz, providing insight into its dynamics following a quantum quench.
Conventional approaches to identifying collective excitations often rely on linear response theory, which can be insufficient for probing dynamics beyond equilibrium. Here, in ‘Quench spectroscopy of amplitude modes in a one-dimensional critical phase’, we report the observation of an underdamped amplitude mode-a symmetry-preserving excitation-emerging in the gapless phase of the one-dimensional XXZ spin chain. Utilizing quantum quenches and supported by Bethe ansatz analysis, we demonstrate this mode’s excitation via oscillations in U(1)-symmetric observables and trace its origin to specific string excitations. Could this quench spectroscopy technique offer a broadly applicable route to characterize collective modes in other strongly correlated systems and beyond?
The Unfolding of Disequilibrium: Introducing the XXZ Spin Chain
The behavior of physical systems rarely conforms to perfect, static equilibrium; instead, most are constantly evolving or responding to external influences. Understanding non-equilibrium dynamics – how systems change over time when perturbed – is therefore fundamental to accurately describing the natural world. This is especially true for systems driven far from stability, where traditional approaches based on equilibrium assumptions break down. Investigating these out-of-equilibrium states allows scientists to explore phenomena like energy transport, relaxation processes, and the emergence of novel phases that are inaccessible under equilibrium conditions. Such studies are not merely academic exercises; they have implications for diverse fields, including materials science, condensed matter physics, and even cosmology, where understanding the early universe requires grappling with systems radically different from those we observe today.
The XXZ spin chain stands as a remarkably adaptable theoretical construct for probing the complexities of quantum many-body systems. This model, rooted in the principles of quantum mechanics, depicts a chain of interacting spins, each possessing a magnetic moment that can align in various directions. The ‘XXZ’ designation refers to the specific types of interactions between neighboring spins – interactions along the x and y axes are equivalent, while the interaction along the z-axis can differ, allowing for a tunable balance between quantum fluctuations and interactions. This flexibility is crucial, as it enables researchers to simulate a diverse range of physical scenarios, from the behavior of magnetism in materials to the dynamics of light propagation in certain optical fibers. By manipulating the strength of these interactions, the XXZ chain can exhibit a spectrum of quantum phases, providing a testing ground for theoretical predictions and a valuable tool for understanding systems driven far from equilibrium – where traditional approaches often fail.
The XXZ spin chain isn’t merely a theoretical construct; its diverse phase diagram serves as a critical benchmark for validating and refining advanced theoretical approaches in condensed matter physics. Beyond possessing a ferromagnetic and antiferromagnetic phase, the chain exhibits a particularly intriguing Luttinger liquid phase – a state characterized by collective excitations and fractionalization of particles, diverging from the behavior of conventional Fermi liquids. This phase, alongside the chain’s quantum critical points separating these distinct behaviors, provides stringent tests for techniques like bosonization, conformal field theory, and dynamical mean-field theory. Accurate prediction of the chain’s properties across its phase diagram – including correlation functions and excitation spectra – confirms the validity of these methods and allows physicists to confidently apply them to more complex, less tractable systems, ultimately advancing understanding of strongly correlated quantum materials.
The XXZ spin chain, when subjected to a ‘quantum quench’ – a sudden alteration of its governing parameters – exhibits a fascinating redistribution of energy. This isn’t simply a settling back to a new, stable state; instead, the system’s energy flows into specific modes, creating a complex pattern of excitations. Researchers analyze this process by tracking how the initial energy injected into the system propagates and thermalizes, revealing details about the chain’s fundamental interactions and its ability to retain ‘memory’ of the initial condition. Detailed studies demonstrate that the speed of this energy propagation-and the ultimate distribution-is strongly dependent on the specific parameters of the quench and the initial state of the chain, offering a powerful tool for probing the interplay between quantum coherence and thermalization in many-body systems. Understanding this dynamic response is crucial for predicting the behavior of similar systems in contexts ranging from condensed matter physics to quantum information processing.
Mapping the Quantum Landscape: The Bethe Ansatz Toolkit
The Bethe ansatz is a mathematical technique used to determine the exact solution for the XXZ spin chain, a model in quantum mechanics describing interacting spins. Unlike perturbative approaches which provide approximate solutions, the Bethe ansatz yields the complete energy spectrum – all possible energy levels and their corresponding states – of the system. This is achieved by mapping the many-body problem onto a set of single-particle equations, allowing for the determination of the system’s eigenstates and eigenvalues. The solution is exact in the sense that it satisfies the Schrödinger equation for the XXZ model without approximation, providing a benchmark for evaluating the accuracy of other methods and offering insights into the system’s behavior, particularly its excited states and their properties.
Rapidities, denoted as \epsilon_i, are a set of parameters that fully define the quasi-particle excitations within the Bethe ansatz solution for the XXZ spin chain. These values are not directly energy or momentum, but rather relate to them through a dispersion relation E = \frac{2\pi}{J} \sum_{j=1}^N \epsilon_j and a related momentum expression, where J is the exchange integral and N is the number of rapidities. Each rapidity is associated with a specific excitation, and the complete set of rapidities determines the system’s energy spectrum. The allowed values of rapidities are constrained by the Bethe ansatz equations, which ensure that the physical states satisfy appropriate boundary conditions and are free from unphysical contributions. Consequently, the rapidities effectively label the eigenstates of the Hamiltonian, and their distribution dictates the system’s macroscopic properties.
In the Bethe ansatz solution of the XXZ spin chain, rapidities are not isolated values but can combine to form ‘strings’. These strings represent collective excitations where multiple rapidities are bound together, behaving as a single quasi-particle. The number of rapidities within a string dictates its properties; a string of length n indicates a collective excitation involving n individual spin flips. Crucially, the energy of a string is determined by the rapidities it contains, and the momentum is related to the string’s overall configuration. The formation of strings significantly alters the excitation spectrum, leading to a characteristic pattern of energy levels that differs from a system with only isolated excitations; understanding string formation is therefore essential for fully characterizing the system’s behavior.
The configuration of rapidities within the Bethe ansatz solution directly determines the system’s dynamical properties. Specifically, arrangements like the ‘two-particle-two-hole’ configuration – where two rapidities representing excitations are separated by two ‘holes’ or unoccupied states – signify the presence of bound states and collective modes. Analyzing these configurations allows for the calculation of correlation functions and response functions, providing insight into how the system evolves in time. The number and distribution of particles and holes within the rapidities configuration directly relate to the number of excitations and their associated momenta, enabling a complete characterization of the system’s dynamical behavior and revealing information about its energy spectrum and scattering processes.
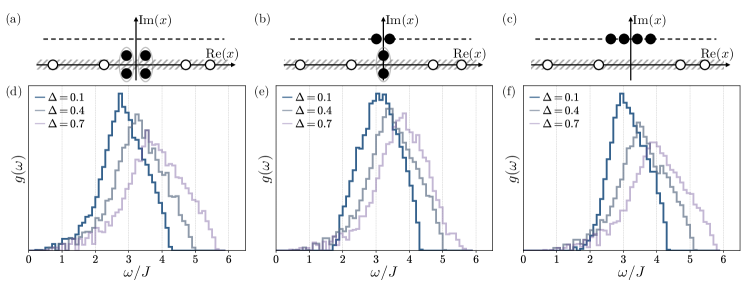
Collective Whispers: Unveiling Symmetry and Excitations
The amplitude mode in the XXZ spin chain represents a collective excitation where spins oscillate in a coordinated manner, deviating from their equilibrium alignment. This is not a single spin flipping, but rather a wave-like perturbation propagating through the spin order. Characterized by a specific frequency and wavelength, the amplitude mode arises from the interactions between spins and is fundamentally linked to the chain’s magnetic ordering. Analysis reveals that this mode is present even at finite temperatures, though its characteristics, such as damping rate, are temperature-dependent. The collective nature of the excitation is confirmed through calculations of the dynamic structure factor, which exhibits a prominent peak corresponding to the amplitude mode’s energy.
The U(1) symmetry of the XXZ spin chain dictates invariance under continuous rotations of the spin components in the xy-plane. This symmetry directly enables the existence of collective excitations like the amplitude mode, as it allows for coherent, phase-preserving oscillations of the spin order parameter. Specifically, the U(1) symmetry implies that any superposition of spin rotations is also a valid state, providing the necessary degeneracy for a gapless mode. The amplitude mode represents a fluctuation in the overall magnetization direction, and the continuous nature of the U(1) symmetry ensures this fluctuation can occur at arbitrarily small energies, manifesting as a well-defined excitation in the system’s energy spectrum. The breaking or reduction of this symmetry, for example through an external magnetic field, would generally lead to the suppression or modification of the amplitude mode.
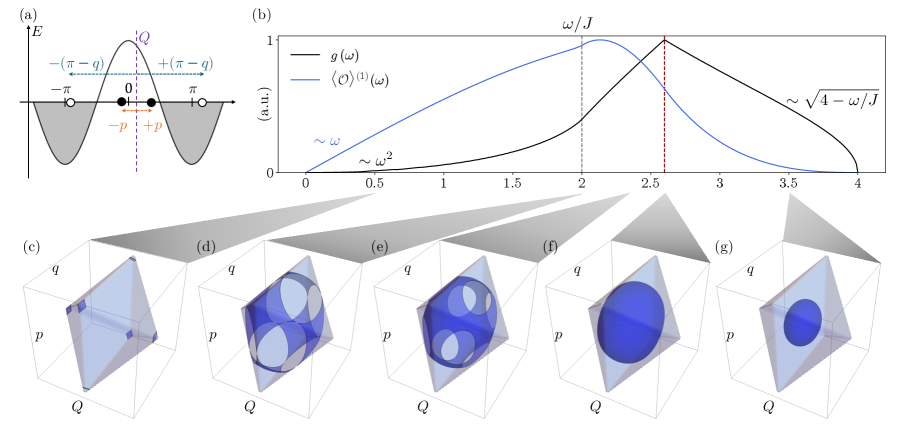
The density of states (DOS) provides insight into the emergence of collective excitations like the amplitude mode by revealing the distribution of allowed energy levels within the system. Specifically, singularities in the DOS, such as the Van Hove singularity, pinpoint energies where a significant accumulation of states occurs. These singular points correspond to crucial energy levels where even small perturbations can induce collective behavior. The amplitude mode, representing a collective oscillation of spin order, manifests as a distinct feature within the DOS, identifiable by its characteristic energy and spectral weight. Analyzing the DOS allows for the prediction and confirmation of such collective excitations and their associated energy scales, offering a direct connection between the microscopic Hamiltonian and macroscopic observables.
Analysis of the XXZ spin chain reveals an underdamped amplitude mode, a collective excitation characterized by an oscillation frequency of approximately 2.5J. This frequency was determined through computational analysis utilizing a system size of N = 100 spins. The ‘underdamped’ designation indicates that the oscillation persists for a relatively long duration due to minimal energy dissipation. The observed frequency is a key parameter defining the dynamic behavior of the spin order within the XXZ chain and serves as a benchmark for validating theoretical models and simulations.
Collective excitations analogous to the amplitude mode observed in the XXZ spin chain also manifest in systems governed by different symmetries. Specifically, the Ising model, characterized by ℤ₂ symmetry – which restricts spins to align either parallel or anti-parallel – exhibits similar low-energy, collective oscillations. While the underlying mechanisms differ due to the distinct symmetry groups, the emergence of these excitations demonstrates a broader phenomenon where collective behavior isn’t solely dictated by a model’s specific details, but also by its inherent symmetries and the resulting constraints on spin configurations. This suggests a potential universality in the types of collective modes that can arise across a range of quantum systems.
Tracing the Echoes of Disruption: Implications for Non-Equilibrium Dynamics
The intricate dance of quantum systems following a sudden disruption-a ‘quantum quench’-can be charted with surprising precision through the Bethe ansatz. This powerful mathematical technique, when combined with an examination of the system’s collective excitations – the coordinated movements of many particles – provides a pathway to forecasting its future state. Rather than simply observing randomness, this approach reveals how energy disperses among different vibrational and quantum modes over time. Consequently, researchers can predict not just if a system will reach a new equilibrium, but how it will do so, offering detailed insights into the relaxation process and potentially revealing exotic states of matter that emerge far from thermal balance. This predictive capability is crucial for understanding the behavior of isolated quantum systems, where interactions are paramount and traditional methods of statistical mechanics often fail.
The redistribution of energy following a quantum quench is revealed through detailed analysis of the system’s modes, demonstrating how initial energy localized in specific degrees of freedom disperses and ultimately establishes a new equilibrium. This process isn’t simply a chaotic dissipation; rather, energy flows preferentially into certain modes dictated by the system’s inherent properties, resulting in a potentially thermalized state characterized by a predictable energy distribution. The analysis shows that while a full approach to thermal equilibrium is expected, transient oscillations and deviations can occur, offering a window into the intricate dance of energy transfer at the quantum level. Understanding this dynamic allows for precise predictions about the system’s evolution and offers valuable insights into how complex quantum systems relax and stabilize after being disturbed from equilibrium.
The analytical power of the Bethe ansatz solution, while limited to specific models, serves as a crucial testing ground for the approximations commonly employed when investigating more intricate physical systems. Many-body physics often necessitates simplified methods – such as perturbation theory or mean-field approximations – to tackle the complexities arising from strong interactions. By providing an exact solution for a solvable model, this work establishes a stringent benchmark against which the accuracy and limitations of these approximations can be rigorously assessed. Researchers can compare the results obtained from approximate methods to the exact Bethe ansatz solution, gaining valuable insights into the regimes where these approximations are valid and identifying the sources of error when discrepancies arise. This process refines computational techniques and theoretical frameworks, ultimately enhancing the ability to model and predict the behavior of a broader range of complex quantum systems.
Theoretical predictions indicate the potential observability of the amplitude mode – a collective excitation arising from quantum spin interactions – within materials possessing specific magnetic properties. Cs2CoCl4, a quasi-one-dimensional antiferromagnet characterized by an anisotropy deviation of approximately Δ ≈ 0.12, stands out as a promising candidate for experimental verification. This material’s particular magnetic configuration enhances the amplitude mode’s signature, suggesting it could be detected through techniques sensitive to dynamic spin correlations, such as neutron scattering or resonant inelastic X-ray scattering. Observing this mode in Cs2CoCl4 would not only validate the theoretical framework developed but also offer a crucial benchmark for understanding energy redistribution and thermalization processes in more complex quantum systems, potentially bridging the gap between theoretical models and experimental observation in the field of non-equilibrium dynamics.
The true power of this theoretical framework lies in its ability to bridge the gap between abstract calculations and measurable phenomena, thereby illuminating the intricacies of non-equilibrium dynamics across a broad spectrum of physical systems. By explicitly connecting the predicted behavior – such as the redistribution of energy following a quantum quench – to observable quantities like the amplitude mode in materials such as Cs2CoCl4, researchers gain a powerful tool for validating and refining their models. This connection isn’t merely about confirming predictions; it provides a pathway to extrapolate understanding from precisely solvable models to more complex, less tractable scenarios found in condensed matter physics, quantum information, and beyond. Consequently, this approach fosters a deeper, more nuanced comprehension of how systems evolve far from equilibrium, potentially unlocking new strategies for controlling and harnessing these dynamic processes.
The study of this critical phase, and the identification of the underdamped amplitude mode within it, reveals a system responding to disturbance not with immediate decay, but with a measurable, sustained oscillation. This echoes Carl Sagan’s observation that “Somewhere, something incredible is waiting to be known.” The researchers don’t merely document a transient excitation from a quantum quench; they trace its lineage to fundamental string excitations within the Bethe ansatz framework, essentially mapping the system’s chronicle. The persistence of this mode, even as the system evolves, suggests an inherent resilience – a graceful aging process within the constraints of time itself, demonstrating that even within complex quantum systems, echoes of initial conditions can resonate long after the initiating event.
What Lies Ahead?
The identification of this underdamped amplitude mode, while a step towards charting the complexities of the one-dimensional critical phase, merely clarifies a local feature within a landscape perpetually yielding to decay. Uptime, in this context, represents a rare phase of temporal harmony-a transient resistance to the inevitable dissolution of excited states. The paper demonstrates excitation via quantum quench, but the precise mechanisms governing the mode’s ultimate fate-its coupling to other degrees of freedom, the subtle erosion of its coherence-remain largely unexplored. Technical debt, analogous to the accumulation of imperfections within any extended system, will invariably diminish its initial clarity.
Future investigations must address the limitations inherent in current analytical approaches. The Bethe ansatz, while powerful, offers a static picture. Extending this framework to incorporate the dynamic effects of external perturbations-those driving the quenches-is a significant undertaking. Furthermore, probing the mode’s behavior in the presence of disorder, or within more complex many-body systems, will reveal the extent to which this behavior is a robust feature of the gapless phase, or merely a fragile artifact of idealization.
Ultimately, the challenge lies not in achieving perfect preservation-an impossibility-but in understanding the precise character of the system’s degradation. The long-term evolution of this amplitude mode, its eventual fragmentation into a sea of entangled excitations, offers a compelling window into the fundamental principles governing the flow of information and energy in a closed quantum system-a system destined, like all others, to return to equilibrium.
Original article: https://arxiv.org/pdf/2601.20926.pdf
Contact the author: https://www.linkedin.com/in/avetisyan/
See also:
- Best Controller Settings for ARC Raiders
- Ashes of Creation Rogue Guide for Beginners
- DCU Nightwing Contender Addresses Casting Rumors & Reveals His Other Dream DC Role [Exclusive]
- Stephen Colbert Jokes This Could Be Next Job After Late Show Canceled
- Is XRP ETF the New Stock Market Rockstar? Find Out Why Everyone’s Obsessed!
- 7 Home Alone Moments That Still Make No Sense (And #2 Is a Plot Hole)
- 10 X-Men Batman Could Beat (Ranked By How Hard It’d Be)
- Best Werewolf Movies (October 2025)
- 10 Ridley Scott Films With the Highest Audience Scores on Rotten Tomatoes
- All 6 Takopi’s Original Sin Episodes, Ranked
2026-01-31 04:59