The Extremal Edge: Black Hole Collapse Defies Cosmic Limits

Author: Denis Avetisyan

New research demonstrates a violation of the third law of black hole mechanics, revealing that highly rotating black holes can form through gravitational collapse in five dimensions.

With a gluing solution of type (i) and <span class="katex-eq" data-katex-display="false">A_k = 2k = 2g</span>, the empirical limit of <span class="katex-eq" data-katex-display="false">\mathcal{B}</span> is reached at a point where, despite <span class="katex-eq" data-katex-display="false">J = 0</span>, the effective magnetic moment <span class="katex-eq" data-katex-display="false">m_H</span> remains positive at <span class="katex-eq" data-katex-display="false">V = 0</span>. — With a gluing solution of type (i) and $A_k = 2k = 2g$ , the empirical limit of $\mathcal{B}$ is reached at a point where, despite $J = 0$ , the effective magnetic moment $m_H$ remains positive at $V = 0$ .

Numerical relativity simulations confirm the formation of extremal Myers-Perry black holes, challenging long-held assumptions about the limits of black hole formation in vacuum gravity.

A cornerstone of classical black hole thermodynamics is the third law, positing the impossibility of reaching an extremal black hole in finite time-however, this is now challenged. In the paper ‘Violation of the third law of black hole mechanics in vacuum gravity’, we present numerical solutions in five-dimensional vacuum gravity demonstrating the finite-time formation of extremal rotating $Myers-Perry$ black holes both from gravitational collapse and directly from vacuum initial data. This constitutes the first confirmed violation of the third law independently of any matter content, fundamentally questioning its universality. Could these findings necessitate a revision of our understanding of black hole horizons and the limits of classical general relativity?

The Universe Sculpted by Spacetime

The very foundation of black hole mechanics rests upon Albert Einstein’s theory of General Relativity, a revolutionary shift in how gravity and spacetime are understood. Rather than viewing gravity as a simple force, General Relativity describes it as a curvature of spacetime caused by mass and energy. This curvature dictates how objects move, and in the case of black holes – objects with immense density – the curvature becomes infinitely strong, creating a point of no return known as the event horizon. The mathematical framework provided by General Relativity allows physicists to not only predict the existence of black holes, but also to describe their properties – such as mass, charge, and angular momentum – and how they interact with their surroundings. Consequently, every aspect of black hole study, from their formation and evolution to their impact on the universe, is intrinsically linked to the principles of warped spacetime and gravitational dynamics established by Einstein’s groundbreaking work.

Black hole mechanics, a surprising field of study, reveals that these seemingly destructive cosmic entities aren’t lawless voids, but rather systems governed by a set of principles strikingly similar to those governing everyday thermodynamics. Just as the first law of thermodynamics concerns energy conservation, black holes adhere to a corresponding law relating changes in mass to alterations in their surface area and angular momentum. Furthermore, the concept of entropy, traditionally linked to disorder, finds a parallel in the black hole’s surface area – a larger area signifies greater entropy. This analogy isn’t merely conceptual; it suggests a deep connection between gravity, thermodynamics, and information theory, hinting that the laws governing black holes may be fundamental aspects of the universe itself and potentially offering insights into the very nature of entropy and information loss. $A = 4\pi r^2$

The Third Law of Black Hole Mechanics posits a fundamental limit on how much a black hole’s properties can change over time. Much like its thermodynamic namesake, this law asserts that achieving absolute zero temperature – or, in the black hole context, zero surface gravity – requires an infinite number of physical processes. This isn’t simply a statement about temperature; it profoundly restricts the ways black holes can evolve. For instance, a black hole cannot ‘completely disappear’ through Hawking radiation in a finite amount of time, as doing so would necessitate reaching zero mass – a violation of the Third Law. This principle, formalized by Jacob Bekenstein and Stephen Hawking, doesn’t prevent black holes from shrinking, but rather dictates that the process has a lower bound on its speed. Consequently, the Third Law establishes a crucial connection between gravity, thermodynamics, and the ultimate fate of these enigmatic cosmic objects, suggesting that even in the most extreme environments, physical laws impose inherent limitations on change.

The exploration of black hole mechanics isn’t merely an exercise in astrophysics; it represents a fundamental probe into the boundaries of physical law. By rigorously examining the constraints imposed on black holes – objects where gravity reigns supreme – physicists can test the very foundations of general relativity and quantum mechanics. These studies reveal that the laws governing black holes bear striking parallels to thermodynamics, suggesting a deep connection between gravity, information, and entropy. Consequently, investigations into these exotic objects offer a unique perspective on the nature of spacetime, potentially revealing where current physical models break down and hinting at the need for a more complete theory that unifies all forces. The insights gained from black hole mechanics are therefore crucial for understanding not only the most extreme environments in the universe, but also the fundamental principles that govern reality itself.

Challenges to Extremality: The Influence of Matter

The Third Law of black hole thermodynamics, which postulates the impossibility of reaching an extremal black hole in a finite number of physical processes, is not universally valid across all matter configurations. Specifically, models incorporating “Thin Shell Matter” – where matter is concentrated on a surface rather than distributed throughout a volume – demonstrate violations of the Third Law. These configurations allow for the construction of rotating black holes with arbitrarily small angular momentum, effectively circumventing the law’s prohibition against reaching an extremal state. This occurs because the surface charge density and angular momentum are decoupled from the black hole’s event horizon in these models, providing a mechanism to continually reduce the black hole’s angular momentum without violating thermodynamic constraints.

Early investigations into the Third Law of black hole mechanics often relied on the assumption of ‘Smooth Matter’, characterized by continuously differentiable energy density. This model initially suggested adherence to the law, preventing the attainment of an extremal black hole state. However, the Kehle-Unger argument, utilizing mathematically permissible but highly oscillatory matter configurations – even those with high differentiability – demonstrated that it is possible to circumvent the Third Law. Specifically, they showed that by carefully constructing matter distributions with increasingly rapid oscillations near the black hole horizon, one can continually lower the energy of the black hole without reaching a minimum, thus violating the Third Law’s prohibition against reducing the surface gravity to zero.

The question of what prevents a black hole from reaching an extremal state-a theoretical limit of charge and angular momentum-centers on the existence of mechanisms that halt the continued influx of energy. While the Third Law of Black Hole Mechanics postulates that it’s impossible to reach this limit, violations observed with specific matter configurations suggest otherwise. The core issue isn’t necessarily a breakdown of the law itself, but rather an incomplete understanding of how matter influences the black hole’s horizon. Specifically, the continued addition of energy, even infinitesimally, requires overcoming a potential barrier that is dictated by the black hole’s properties and the characteristics of the infalling matter. If this barrier can be circumvented – as demonstrated by models incorporating ‘Thin Shell Matter’ – the black hole can, theoretically, continue to accumulate charge and angular momentum, approaching and potentially surpassing the extremal limit. Determining the precise nature of this barrier and the factors that modulate its strength is therefore crucial to resolving this challenge to the Third Law.

Current research indicates that the validity of the Third Law of Black Hole Thermodynamics is heavily dependent on the specific matter configuration surrounding the black hole. While initial models utilizing ‘smooth matter’ suggested potential adherence to the law, subsequent theoretical work, notably the Kehle-Unger argument, has demonstrated that even highly differentiable matter distributions can, under certain conditions, allow for the circumvention of the Third Law by enabling states of arbitrarily small but non-zero angular momentum and electric charge. This necessitates a more comprehensive investigation into the relationship between matter properties – including its distribution, equation of state, and potential for exotic forms – and the black hole’s ability to approach an extremal state; such investigation is crucial for refining current theoretical frameworks and potentially identifying new constraints on black hole behavior.

Constructing Spacetime: Numerical Approaches

Analytical solutions to Einstein’s field equations, while valuable, are limited to highly symmetric scenarios. Numerical relativity employs computational techniques to approximate solutions for more complex and realistic black hole spacetimes, including those arising from binary black hole mergers or gravitational waves. These methods discretize spacetime into a grid and iteratively solve the field equations on that grid. The resulting solutions, though approximate, allow physicists to analyze phenomena inaccessible through analytical approaches, such as the dynamics of strong gravitational fields and the emission of gravitational radiation. Validation of these numerical solutions relies on convergence testing, where grid spacing is systematically refined to demonstrate that the computed results approach a consistent limit, and comparison with known analytical solutions where available.

Characteristic gluing is a numerical relativity technique used to construct spacetime solutions by evolving gravitational waves in regions of spacetime and then “gluing” these regions together. This method utilizes double null coordinates $(u, v)$ , which align null surfaces with the coordinate lines, enabling efficient modeling of wave propagation as information travels along these surfaces. By constructing solutions on intersecting null surfaces, the technique avoids the need to solve for an initial hypersurface, simplifying the computational process and allowing for the direct construction of dynamical spacetimes. The use of double null coordinates inherently simplifies the equations governing wave propagation, reducing computational cost and increasing the accuracy of the resulting spacetime solutions.

High-order numerical methods, specifically the Spectral Element Discontinuous Galerkin Method, are essential for constructing accurate and stable spacetime solutions in numerical relativity. This method achieves demonstrated convergence rates of 6.20527 for the $g_{Ne,n}$ metric component when employing h-refinement-a process of systematically reducing element size. This observed convergence rate indicates that the error in the solution decreases proportionally to $h^{6.20527}$ , where h represents the characteristic element size. Such high-order accuracy is critical for minimizing numerical errors and reliably simulating the dynamics of black hole spacetimes, particularly when resolving strong gravitational fields and rapidly changing waveforms.

The construction of realistic spacetime solutions in numerical relativity, specifically through techniques like characteristic gluing, necessitates the utilization of special functions to accurately represent and compute the necessary integrals. The Incomplete Beta Function, $B(x; a, b)$ , is particularly crucial for evaluating the integrals arising from the matching of solutions across the gluing surface. This function arises naturally when transforming between different coordinate systems and ensuring continuity of the metric and its derivatives. Accurate computation of these integrals, facilitated by the Incomplete Beta Function, directly impacts the fidelity of the resulting spacetime and the validity of subsequent physical simulations; without precise evaluation, numerical errors accumulate, compromising the overall accuracy of the solution.

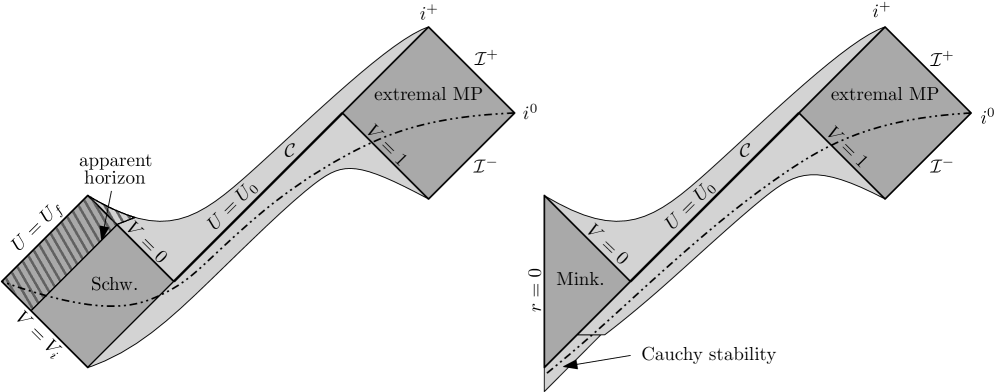
Penrose diagrams illustrate the gluing constructions for two spacetime types, demonstrating that solutions derived from characteristic initial/final value problems (lightly shaded) can be isometrically embedded within Schwarzschild, extremal, and Minkowski spacetimes, with the striped region indicating trapped surfaces bounded by the apparent horizon and Cauchy stability enabling extension to the center of symmetry <span class="katex-eq" data-katex-display="false">r=0</span> in the right panel. — Penrose diagrams illustrate the gluing constructions for two spacetime types, demonstrating that solutions derived from characteristic initial/final value problems (lightly shaded) can be isometrically embedded within Schwarzschild, extremal, and Minkowski spacetimes, with the striped region indicating trapped surfaces bounded by the apparent horizon and Cauchy stability enabling extension to the center of symmetry $r=0$ in the right panel.

Beyond Simplification: Symmetry and Higher Dimensions

The study of black holes possessing symmetries, notably the Myers-Perry black hole defined by SU(2) and SU(2)xU(1) symmetries, provides a crucial pathway to understanding their complex behaviors. These symmetries aren’t merely mathematical conveniences; they fundamentally constrain the black hole’s geometry and allow physicists to construct exact solutions to Einstein’s field equations. By leveraging these symmetries, researchers can explore how black holes rotate, become charged, or interact with surrounding matter in ways that are analytically tractable. The resulting insights reveal the intricate relationship between a black hole’s symmetry group and its physical properties, offering a deeper comprehension of gravitational phenomena in extreme environments and potentially illuminating the fundamental nature of spacetime itself.

Cohomogeneity-1 spacetimes offer a powerful reduction in complexity when analyzing black hole solutions, particularly in higher-dimensional scenarios. This mathematical framework leverages symmetry to constrain the problem, effectively reducing it from a fully general, and often intractable, partial differential equation to a set of ordinary differential equations. By demanding that the spacetime possesses a one-parameter group of symmetries acting on a two-dimensional surface, researchers can significantly simplify the calculations needed to determine the black hole’s properties – such as its mass, charge, and angular momentum. This approach isn’t merely a computational trick; it allows for a deeper understanding of the underlying physics by isolating key features and revealing patterns that might otherwise remain hidden within the full complexity of the spacetime. Consequently, studies utilizing cohomogeneity-1 spacetimes, like those involving the Myers-Perry black hole, provide valuable insights into the behavior of gravity in extreme environments and the formation of these exotic objects.

Investigations into the interplay between Vlasov matter and Reissner-Nordström black holes reveal nuanced details regarding matter-black hole interactions, particularly when considering the influence of massless charged scalar fields. These studies demonstrate how self-gravitating scalar fields, modeled by Vlasov dynamics, respond to the gravitational pull of charged black holes, creating a complex feedback loop. The presence of a charge on the black hole fundamentally alters the dynamics of the scalar field, leading to phenomena such as enhanced accretion or the formation of characteristic field structures around the event horizon. By analyzing these solutions, researchers gain insight into how matter distribution affects the spacetime geometry and vice versa, providing a more complete picture of gravitational interactions in extreme environments. The dependence on massless scalar fields allows for exploring scenarios where quantum effects may become significant, bridging classical general relativity with potential quantum gravity considerations.

Recent research has confirmed the existence of solutions in five-dimensional vacuum gravity that defy the conventional third law of thermodynamics, which dictates that achieving absolute zero temperature requires infinite time. Through rigorous numerical analysis of the $fNe,n$ metric, convergence rates of 6.54804 were observed using h-refinement techniques, indicating a rapid approach to extremality. Further validation came from p-refinement, demonstrating exponential convergence with values of 0.58376 and 0.545154. These findings not only challenge established thermodynamic principles but also provide strong evidence supporting the theoretical prediction that Myers-Perry black holes-rotating black holes in higher dimensions-can indeed form in a finite amount of time, offering crucial insights into the dynamics of gravity in extreme environments.

The exploration of black hole solutions within higher-dimensional spacetimes carries profound implications for theoretical physics, challenging established notions of gravity and the structure of spacetime itself. By rigorously examining these complex geometries-particularly those exhibiting specific symmetries-research reveals that classical general relativity may not fully describe gravitational phenomena in dimensions beyond the familiar four. The observed convergence rates in numerical simulations, specifically for metrics like fNe,n, don’t merely confirm the existence of Myers-Perry black holes, but also suggest the possibility of spacetime singularities forming in finite time-a stark departure from the cosmic censorship hypothesis. This necessitates a re-evaluation of fundamental assumptions about the behavior of gravity under extreme conditions and opens avenues for exploring modified theories of gravity, potentially bridging the gap between general relativity and quantum gravity, and offering new perspectives on the very fabric of reality.

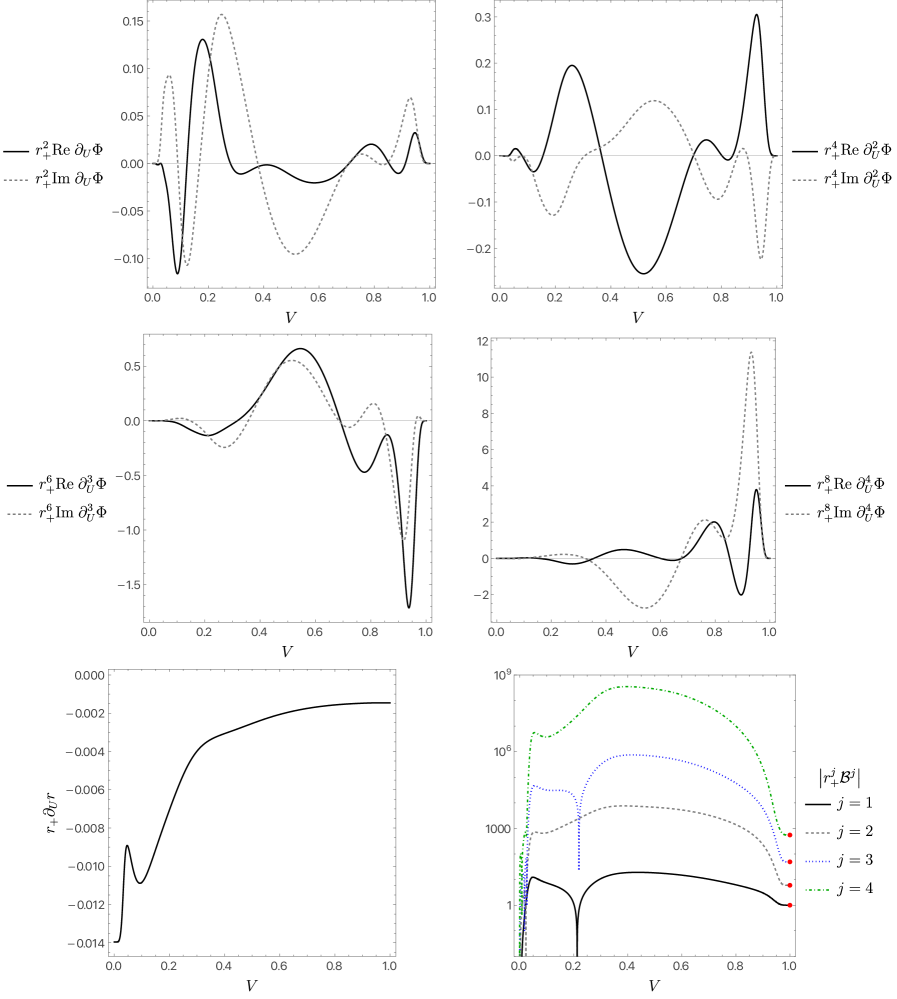
Type II solutions exhibit large <span class="katex-eq" data-katex-display="false">\mathcal{B}^{j}</span> field magnitudes, displayed on a logarithmic scale, with red disks indicating empirical mode matching values, alongside plots of Φ derivatives. — Type II solutions exhibit large $\mathcal{B}^{j}$ field magnitudes, displayed on a logarithmic scale, with red disks indicating empirical mode matching values, alongside plots of Φ derivatives.

The pursuit of understanding extremal black holes, as demonstrated in this work concerning the third law of black hole mechanics, echoes a similar dedication to paring away complexity. This research meticulously constructs solutions describing gravitational collapse, revealing the formation of these objects in five dimensions. It is a process of refinement – seeking the essential characteristics of these phenomena by eliminating extraneous factors. As Leonardo da Vinci observed, “Simplicity is the ultimate sophistication.” The study’s focus on vacuum gravity and Myers-Perry black holes embodies this principle, arriving at fundamental truths through a deliberate reduction to core components.

Where Do We Go From Here?

The demonstration of third law violation, even within the admittedly constrained landscape of five-dimensional vacuum gravity, feels less like a destination and more like the removal of a particularly ornate signpost. The field had, for a time, convinced itself that the third law was a fundamental constraint, a kind of gravitational inertia. To find it yielding under scrutiny suggests the deeper structure may be less about inviolable principles and more about the limits of our current formalism. They called it a law; it was, perhaps, merely a well-maintained expectation.

The natural progression involves extending this analysis beyond the cohomogeneity assumptions inherent in Myers-Perry solutions. True progress will demand a move towards genuinely dynamical spacetimes, examining the collapse of perturbations and the formation of horizons through numerical relativity – a task, it must be said, frequently undertaken with enthusiasm and rarely with elegance. Simplicity, in this arena, is not merely desirable; it’s a prerequisite for discerning signal from noise.

Ultimately, the question is not whether the third law always fails, but whether it represents a fundamental property of gravity or an artifact of our preference for mathematically tractable solutions. The pursuit of such clarity may lead, predictably, to more complicated mathematics. One hopes, however, that the field remembers that the goal is understanding, not accumulation.

Original article: https://arxiv.org/pdf/2601.20955.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/

The Universe Sculpted by Spacetime

Challenges to Extremality: The Influence of Matter

Constructing Spacetime: Numerical Approaches

Beyond Simplification: Symmetry and Higher Dimensions

Where Do We Go From Here?

See also: