Quark Matter Under Magnetar Fields: A New Framework for Superconductivity

Author: Denis Avetisyan

A novel approach combining medium separation with magnetic field regularization offers a more physically realistic model for understanding the behavior of dense quark matter in extreme astrophysical environments.

The study demonstrates how constituent quark mass and diquark condensate shift in response to magnetic field strength, with comparisons between nMFIR, MFIR, and MFIR + MSS models revealing nuanced dependencies crucial for understanding the behavior of matter under extreme conditions.

This study demonstrates that combining the Medium Separation Scheme with Magnetic Field Independent Regularization provides a robust and consistent description of color superconductivity in magnetized, cold two-flavor quark matter at finite density.

The accurate description of dense quark matter-particularly its superconducting phases under strong magnetic fields-remains challenging due to model-dependent ambiguities in handling medium effects and divergences. This work, ‘Medium separation scheme effects on the magnetized and cold two-flavor superconducting quark matter’, investigates the impact of employing a combined Magnetic Field Independent Regularization (MFIR) and Medium Separation Scheme (MSS) within the Nambu-Jona-Lasinio model. Our findings demonstrate that this approach effectively suppresses spurious oscillations-often misinterpreted as physical phenomena-and ensures physically consistent high-density behavior of the diquark condensate, yielding a positive magnetization across the explored parameter space. Could this refined framework provide a more reliable pathway towards understanding the complex interplay between superconductivity, magnetism, and density in these extreme astrophysical environments?

The Allure of Quark Matter: A Window into Extreme Physics

Deep within the cores of neutron stars and in the fleeting moments following the Big Bang exists a remarkable state of matter known as quark matter. Typically, quarks-the fundamental constituents of protons and neutrons-are confined within these particles by the strong nuclear force. However, under the immense pressure and density found in these extreme environments, this confinement breaks down, liberating the quarks and gluons. This deconfined state isn’t simply a plasma of free quarks; it’s a complex, potentially superfluid liquid where quarks and gluons interact in ways not fully understood. The existence of quark matter fundamentally alters the equation of state of ultra-dense matter, impacting the maximum mass of neutron stars and influencing the dynamics of core-collapse supernovae, offering a unique window into the very fabric of reality at its most fundamental level.

Investigating the properties of quark matter presents a significant challenge to conventional theoretical approaches. The standard methods of Quantum Chromodynamics (QCD), known as perturbative calculations, rely on approximating interactions as small deviations from free particles – a technique that breaks down under the extreme densities and temperatures where quark matter exists. These conditions force quarks and gluons into a strongly coupled regime, where interactions are so intense that they fundamentally alter the behavior of the particles. Consequently, researchers must employ non-perturbative techniques, such as lattice QCD – a computationally intensive method that discretizes spacetime – or effective field theories to model the complex dynamics at play. These alternative approaches strive to capture the emergent phenomena arising from strong interactions, offering a pathway to understand the exotic phases and collective behavior expected within this extreme state of matter and ultimately, the nature of neutron stars and the early universe.

Under the immense pressures and temperatures found within neutron stars or the very early universe, quarks-typically confined within protons and neutrons-enter a state of deconfined matter where their interactions become extraordinarily complex. This isn’t simply a gas of free quarks; rather, strong force dynamics dictate the formation of intricate correlations and potentially entirely new phases of matter. Theoretical models suggest the possibility of color superconductivity, where quarks pair up and exhibit zero electrical resistance, or even quarkyonic matter, a state exhibiting properties of both quarks and hadrons. These exotic phases aren’t merely theoretical curiosities; their existence would dramatically alter the equation of state of ultra-dense matter, influencing the stability and structure of neutron stars and impacting the dynamics of core-collapse supernovae. Precisely mapping these interactions and identifying the resulting phases remains a central challenge in modern physics, demanding sophisticated theoretical calculations and experimental probes of extreme environments.

Accurately characterizing quark matter holds profound implications for resolving key puzzles in both astrophysics and cosmology. The equation of state – the relationship between pressure and density – of this exotic substance dictates the maximum mass and radius of neutron stars, offering a crucial observational test for theoretical models. Furthermore, understanding the behavior of quark matter in the extremely early universe is essential for modeling the conditions immediately following the Big Bang and potentially explaining the origin of cosmic phenomena like heavy ion collisions. Simulations of both neutron star mergers and the primordial universe critically depend on reliable parameters describing quark matter’s thermal and mechanical properties; therefore, refinements in these calculations promise to illuminate the evolution of the cosmos and the life cycle of stellar remnants. $P = \rho c^2$ represents a simplified view, but precise determinations of such relationships are vital for advancing our comprehension of these extreme environments.

The normalized quark mass <span class="katex-eq" data-katex-display="false">M/M_0</span> exhibits a consistent relationship with <span class="katex-eq" data-katex-display="false">e_B</span> for <span class="katex-eq" data-katex-display="false">G_D/G_S = 0.0</span>, demonstrating comparable results between the MFIR and nMFIR methods. — The normalized quark mass $M/M_0$ exhibits a consistent relationship with $e_B$ for $G_D/G_S = 0.0$ , demonstrating comparable results between the MFIR and nMFIR methods.

The NJL Model: A Framework for Decoding Dense Quark Matter

The Nambu-Jona-Lasinio (NJL) model is a four-fermion interaction model used in particle physics to describe the non-perturbative regime of Quantum Chromodynamics (QCD). Unlike perturbative QCD, which relies on expansions in the coupling constant and fails at high densities, the NJL model provides a framework for studying quark interactions when the strong coupling prevents standard perturbation theory. It effectively models the interaction between quarks through an effective Lagrangian containing a four-quark interaction term, allowing investigation of phenomena that occur at energy scales where perturbative calculations are unreliable. This approach is particularly useful for exploring the behavior of quark matter under extreme conditions, such as those found in neutron stars or during heavy-ion collisions, where quark degrees of freedom become relevant.

The Nambu-Jona-Lasinio (NJL) model facilitates the study of chiral symmetry breaking, a phenomenon where the symmetry between left- and right-handed quarks is spontaneously broken in the vacuum, leading to the generation of mass for quarks. This breaking is characterized by the formation of a quark condensate, $\langle \overline{q}q \rangle$ , representing the vacuum expectation value of the quark-antiquark operator. Non-zero values of this condensate indicate a broken chiral symmetry and are a key signature of the model’s predictions for the behavior of quarks in the low-energy regime and at high densities, providing insights into the properties of strongly interacting matter.

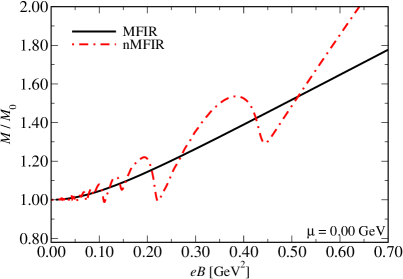
Accurate modeling of quark interactions within the NJL framework necessitates the implementation of regularization schemes to address inherent divergences arising from the integral equations. Standard regularization techniques can introduce spurious oscillations into calculated observables; however, the combined Modified Fermi Integral Regularization (MFIR) and Momentum Subtraction Scheme (MSS) effectively mitigates these artifacts. MFIR focuses on separating the vacuum and medium contributions to the self-energy integrals, while MSS provides a robust method for renormalization. The combined approach ensures a stable and physically meaningful description of dense quark matter by accurately handling the ultraviolet behavior of the theory and providing a consistent framework for calculating finite physical quantities.

Regularization schemes like the Martin-Soker-Sommerfeld (MSS) and the Modified Fermi Integral Regularization (MFIR) are crucial for accurately modeling dense quark matter within the Nambu-Jona-Lasinio (NJL) model. These schemes address divergences inherent in quark field theory by explicitly separating contributions originating from the vacuum-the state with no particles-and those arising from the medium-the dense quark environment. This separation is achieved through careful treatment of the momentum integrals involved in the calculations. By isolating vacuum and medium effects, these regularization methods minimize spurious oscillations often observed in simpler regularization techniques and provide a more physically realistic description of the properties of dense quark matter, such as quark condensate formation and chiral symmetry breaking.

The diquark condensate Δ decreases with increasing chemical potential μ, with the MFIR + MSS calculation exhibiting a notable shift compared to MFIR alone at finite magnetic fields.

Color Superconductivity: Unveiling the Diquark Condensate

Color superconductivity, a state of matter theorized to exist within quark-gluon plasma, originates from the formation of Cooper pairs analogous to conventional superconductivity, but composed of quarks instead of electrons. These quark-Cooper pairs are referred to as diquarks, and their condensation – a macroscopic quantum phenomenon where a significant number of diquarks occupy the lowest energy state – is described by a non-zero diquark condensate $\langle \bar{q}q \rangle$ . This condensate parameter quantifies the average density of diquark pairs and serves as an order parameter for the color superconducting phase. Unlike conventional superconductivity which relies on electromagnetic attraction, the binding force between quarks in a diquark is the strong force, mediated by gluons, resulting in a fundamentally different mechanism for pair formation and a substantially larger superconducting gap.

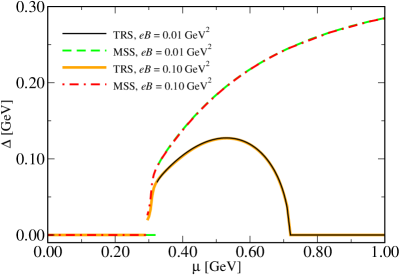
Strong magnetic fields exert a considerable influence on color superconducting phases by altering their fundamental properties. These fields introduce a spatial anisotropy, meaning the superconducting behavior differs depending on the direction within the material. Specifically, the magnetic field modifies the energy gap structure – a key characteristic defining the superconducting state – leading to gap anisotropy and potentially inducing novel pairing symmetries. The magnitude of this impact is directly related to the field strength; higher field strengths generally result in more pronounced modifications to the color superconducting state, affecting both its critical temperature and the quasiparticle excitations within the condensate. This alteration of the gap structure is crucial for understanding the behavior of quark matter under extreme astrophysical conditions.

Application of a magnetic field to color superconducting phases results in anisotropy within the superconducting state, altering its properties. Specifically, the magnetic field introduces a preferred direction, breaking the isotropic nature of the superconducting gap. This manifests as a directional dependence in the energy required to break a Cooper pair – the superconducting gap – leading to different gap magnitudes along different spatial directions. The modification of the gap structure impacts various observables, including the critical field strength required for superconductivity and the density of states at the Fermi surface. The degree of anisotropy and gap modification are dependent on the strength and orientation of the applied magnetic field relative to the superconducting condensate.

The implementation of the Magnetic Field Induced Renormalization (MFIR) scheme alongside the Mean Square Slope (MSS) scheme results in a diquark condensate that exhibits a monotonic increase as the chemical potential increases. This behavior is consistent with predictions derived from multiple theoretical frameworks, including lattice Quantum Chromodynamics (QCD) calculations, chiral perturbation theory, and renormalization-group analyses. Specifically, these methods anticipate a positive correlation between the chemical potential and the condensate value, indicating a strengthening of the diquark pairing interaction with increasing density. The agreement between the MFIR/MSS results and these established theoretical approaches provides further validation for the model’s accuracy in describing color superconducting phases.

The <span class="katex-eq" data-katex-display="false">\mathbb{B} \times \mu</span> phase diagram distinguishes between chiral symmetry breaking, color superconductivity, and normal phases, as demonstrated by the MFIR method and enhanced by the MFIR + MSS approach. — The $\mathbb{B} \times \mu$ phase diagram distinguishes between chiral symmetry breaking, color superconductivity, and normal phases, as demonstrated by the MFIR method and enhanced by the MFIR + MSS approach.

Van Alphen-de Haas Oscillations: Probing the Electronic Landscape

Van Alphen-de Haas (VAHD) oscillations represent a sophisticated experimental technique for dissecting the electronic landscape within materials. These subtle fluctuations in a material’s magnetization, measured under strong magnetic fields at extremely low temperatures, arise from the quantum mechanical behavior of electrons orbiting in closed paths – known as Landau levels. The frequency with which these oscillations occur is inversely proportional to the cross-sectional area of the Fermi surface, a crucial descriptor of the allowed momentum states for electrons. Consequently, by meticulously analyzing the VAHD signal, researchers can map out the shape and size of the Fermi surface with exceptional precision, gaining invaluable insights into a material’s conductivity, magnetic properties, and ultimately, its fundamental electronic structure. This technique proves particularly useful in investigating complex materials where traditional methods fall short, offering a unique window into the quantum realm of solid-state physics.

When a magnetic field is applied to a conducting material, the paths of electrons are no longer free; instead, they curve into circular orbits perpendicular to the field. This behavior results in the quantization of electron motion, meaning electrons can only occupy discrete energy levels known as Landau Levels. These levels are analogous to the energy levels of an electron confined to an atom, but arise from the constraints imposed by the magnetic field. The spacing between Landau Levels is directly proportional to the strength of the magnetic field, and the formation of these quantized levels dramatically alters the electronic properties of the material, allowing researchers to map the material’s Fermi surface and probe its unique quantum characteristics. This principle underpins the Van Alphen-de Haas effect, providing a sensitive measure of these oscillations and ultimately revealing details about the material’s underlying electronic structure.

Van Alphen-de Haas (VAHD) oscillations function as a unique tool for mapping the electronic landscape of materials by meticulously tracking the behavior of electrons in strong magnetic fields. These oscillations emerge because electrons don’t move freely, but rather occupy discrete energy levels, known as Landau levels, when subjected to a magnetic field. The frequency at which these oscillations appear is inversely proportional to the cross-sectional area of the Fermi surface – the boundary in momentum space separating occupied from unoccupied electron states. Consequently, by precisely measuring the oscillation frequency, researchers can deduce the size and shape of the Fermi surface, effectively creating a detailed map of how charge carriers are distributed within the material’s momentum space and providing crucial insights into its electronic properties and behavior. This technique is particularly valuable for understanding complex materials where traditional methods fall short.

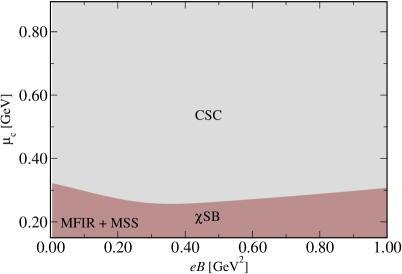
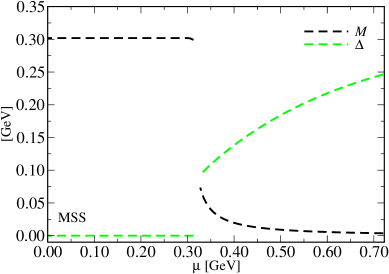
Recent investigations utilizing the Modified Fermi-liquid Interaction and Mean-field Shift (MFIR and MSS) scheme have refined the understanding of phase diagrams in strongly coupled systems, particularly concerning superconductivity under extreme conditions. This approach demonstrates a significant shift in critical lines when plotted on a $\mu \times eB$ plane – where μ represents the chemical potential and $eB$ the magnetic field. Crucially, the MFIR and MSS scheme addresses a previously observed artificial suppression of the superconducting phase at high chemical potentials, a limitation inherent in earlier models. By accurately accounting for interactions and shifts in the energy landscape, this methodology reveals a more realistic phase structure, predicting robust superconductivity even under conditions where conventional calculations would suggest its absence. The result is a more nuanced and dependable framework for interpreting astrophysical observations and furthering understanding of these enigmatic celestial objects.

Comparing time-reversal symmetry (TRS) and manifestly symmetric scheme (MSS) calculations at <span class="katex-eq" data-katex-display="false">e</span> = 0, constituent quark mass and diquark condensate both exhibit dependencies on chemical potential. — Comparing time-reversal symmetry (TRS) and manifestly symmetric scheme (MSS) calculations at $e$ = 0, constituent quark mass and diquark condensate both exhibit dependencies on chemical potential.

Symmetry Breaking and the Trace Anomaly: Charting a Path Forward

The exotic state of matter known as quark matter, theorized to exist within the cores of neutron stars and potentially created in high-energy collisions, doesn’t behave as a simple collection of quarks and gluons. Its properties are fundamentally dictated by the symmetries inherent in Quantum Chromodynamics (QCD), the theory governing the strong nuclear force. These symmetries, while present in the fundamental equations, are often spontaneously broken within quark matter due to complex interactions. This breaking isn’t a flaw, but rather a crucial mechanism that gives rise to the observed mass of hadrons and dictates the matter’s equation of state. Consequently, understanding how these symmetries manifest – or are broken – within quark matter is paramount to deciphering the behavior of ultra-dense baryonic matter and probing the limits of QCD itself; subtle changes in these symmetries directly impact macroscopic properties like the stiffness of neutron stars and the rate of gravitational wave emission from colliding examples.

The trace anomaly, a quantifiable deviation from the predictions of conformal symmetry, serves as a crucial signal for symmetry breaking within quark matter. Conformal symmetry, if unbroken, would dictate a scale-invariant system where physical laws remain unchanged under size transformations; however, the strong force, governed by Quantum Chromodynamics, introduces a scale through its coupling constant. This results in a non-zero trace of the energy-momentum tensor – the trace anomaly – effectively indicating that the theory is not truly scale-invariant at low energies. Measuring this anomaly, represented mathematically as $\Theta = m_q \langle \bar{q}q \rangle$ , where $m_q$ is the quark mass and $\langle \bar{q}q \rangle$ is the quark condensate, provides insights into the dynamics of quarks and gluons, and crucially, constrains the equation of state of ultra-dense matter found within neutron stars. Its presence confirms that the underlying symmetries are broken, influencing the collective behavior of quark matter and impacting observable astrophysical phenomena.

The trace anomaly, a quantifiable deviation from the expected scale invariance in quantum field theories, serves as a crucial diagnostic for the behavior of quark matter at extreme densities. This anomaly directly impacts the equation of state, which dictates the relationship between pressure and energy density within neutron stars. A precise determination of the equation of state is vital for accurately modeling neutron star structure, mass-radius relationships, and ultimately, their stability against collapse. Because the trace anomaly reflects the non-perturbative interactions between quarks and gluons, its accurate calculation-often achieved through sophisticated methods like lattice QCD and effective models-constrains the possible forms of quark matter and offers insights into the fundamental strong force interactions governing matter under the most extreme conditions found in the cosmos. Consequently, the study of the trace anomaly is not merely a theoretical exercise, but a pathway towards understanding the properties of some of the densest objects in the universe.

Recent investigations utilizing the Modified Symmetry Scheme (MSS) have revealed a compelling pathway towards resolving long-standing discrepancies in the study of quark matter. This approach demonstrably facilitates a smoother and more rapid convergence to the conformal limit – a crucial theoretical benchmark – when compared to traditional methods. The MSS achieves this by carefully adjusting the treatment of symmetry breaking, resulting in an equation of state that aligns more closely with predictions derived from fundamental principles. This improved consistency is particularly significant when modeling the extreme conditions found within neutron stars, where the behavior of quark matter dictates observable properties like mass and radius; the MSS therefore offers a more reliable framework for interpreting astrophysical observations and furthering understanding of these enigmatic celestial objects.

The trace anomaly, a key indicator of the quark-gluon plasma phase transition, scales with energy density <span class="katex-eq" data-katex-display="false">\varepsilon</span> normalized to the saturation density <span class="katex-eq" data-katex-display="false">\varepsilon_0</span> in the presence of a magnetic field. — The trace anomaly, a key indicator of the quark-gluon plasma phase transition, scales with energy density $\varepsilon$ normalized to the saturation density $\varepsilon_0$ in the presence of a magnetic field.

The pursuit of a ‘robust and physically consistent framework’ within this study, as demonstrated by combining the Magnetic Field Independent Regularization with the Medium Separation Scheme, reveals a familiar pattern. It echoes a deeply human tendency to construct elaborate systems, believing they’ve tamed the inherent messiness of reality. One is reminded of Immanuel Kant’s observation: “All our knowledge begins with the senses, ends with the understanding.” This work, in its careful attempt to avoid ‘artificial oscillations’ and align with first-principles expectations, showcases the desire for a clean, understandable model – a desire that often obscures the fact that every strategy works-until people start believing in it too much. The authors seek order, but the underlying subject – dense quark matter – remains a realm of complexity where perfect predictability is likely an illusion.

The Horizon Beckons

The pursuit of understanding matter at extreme densities-the stuff of neutron stars, for instance-often feels like chasing a phantom limb. This work, by carefully aligning regularization schemes with the underlying physics, at least provides a more stable footing. It appears the particular arrangement of mathematical scaffolding-here, the marriage of MFIR and MSS-matters less than the avoidance of spurious artifacts. One suspects the true value lies not in the absolute predictions, but in revealing where the model breaks down, and thus, where real physics must intervene.

The tendency to seek neat, easily quantifiable solutions should be viewed with skepticism. Landau levels, while mathematically convenient, are themselves idealizations. The next step isn’t necessarily higher-order calculations, but a more honest accounting for the limitations inherent in treating strongly interacting systems with effectively perturbative methods. The insistence on mathematically ‘elegant’ solutions frequently obscures the messy reality that emergent phenomena rarely respect the boundaries of the chosen formalism.

Bubbles are born from shared excitement and die from lonely realization. The current framework, while improved, remains a map, not the territory. Future explorations should focus on systematically introducing realistic complexities – finite temperature effects, for example, or the influence of hyperons – not to achieve ever-greater precision, but to gauge the model’s resilience. It is in the fractures, the points of inevitable failure, that the most intriguing physics truly resides.

Original article: https://arxiv.org/pdf/2601.21042.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/