The Physics of Thought: Unlocking AI’s Inner Workings

Author: Denis Avetisyan

A new approach, Momentum Attention, leverages principles of Hamiltonian mechanics to illuminate how neural networks learn and make decisions.

A novel transformer architecture, leveraging a momentum-based approach to attention, overcomes the traditional <span class="katex-eq" data-katex-display="false"> N \geq 2 </span> barrier in single-layer induction-achieving 83.4% peak accuracy-and exhibits an attenuated scaling law (<span class="katex-eq" data-katex-display="false"> \gamma^* = 4.17 \times N^{-0.74} </span>) demonstrating that depth and momentum function as interchangeable computational resources, and confirming the theoretical prediction of signal attenuation across layers. — A novel transformer architecture, leveraging a momentum-based approach to attention, overcomes the traditional $N \geq 2$ barrier in single-layer induction-achieving 83.4% peak accuracy-and exhibits an attenuated scaling law ( $\gamma^* = 4.17 \times N^{-0.74}$ ) demonstrating that depth and momentum function as interchangeable computational resources, and confirming the theoretical prediction of signal attenuation across layers.

This paper introduces a symplectic augmentation to Transformer networks, enabling single-layer induction and offering tools for mechanistic interpretability via spectral forensics.

Existing mechanistic interpretability research faces limitations in fully characterizing the dynamics of large language models and achieving efficient induction. This is addressed in ‘Momentum Attention: The Physics of In-Context Learning and Spectral Forensics for Mechanistic Interpretability’, which introduces a symplectic augmentation to Transformer networks-Momentum Attention-that leverages physical conservation laws to enable single-layer induction and direct access to velocity information. By framing attention as a physical circuit, we demonstrate a fundamental duality between kinematic momentum and high-pass filtering, offering novel tools for spectral forensics via Bode plots. Could this framework, bridging generative AI, Hamiltonian physics, and signal processing, unlock a deeper understanding of emergent computation in neural networks?

The Inherent Limits of Attention: Why Scaling Isn’t Enough

Transformers, despite their widespread success in natural language processing, possess an inherent limitation stemming from their DC-coupled architecture, which hinders effective processing of temporal dependencies. This design treats each input token independently, lacking an explicit mechanism to maintain and propagate information across extended sequences; as a result, the model struggles with tasks requiring reasoning about long-range relationships or evolving states. Consequently, simply increasing the size of a standard Transformer model – adding more layers or parameters – eventually yields diminishing returns, leading to performance plateaus. The architecture’s inability to efficiently capture and utilize temporal context represents a fundamental bottleneck, suggesting that alternative approaches are necessary to unlock further advancements in complex, sequential reasoning tasks.

Despite the remarkable success of large language models, scaling transformer architectures alone fails to overcome inherent limitations in sequential data processing. Studies reveal a surprising inefficiency: standard transformers achieve a mere 1.2% accuracy on tasks requiring associative recall – the ability to connect related pieces of information across a sequence. This low score isn’t simply a matter of needing more parameters or training data; it indicates a fundamental bottleneck in how these models handle temporal dependencies. The architecture struggles to effectively retain and utilize information from earlier parts of a sequence when processing later elements, suggesting that simply increasing scale delivers diminishing returns and necessitates exploration of alternative approaches to sequential modeling.

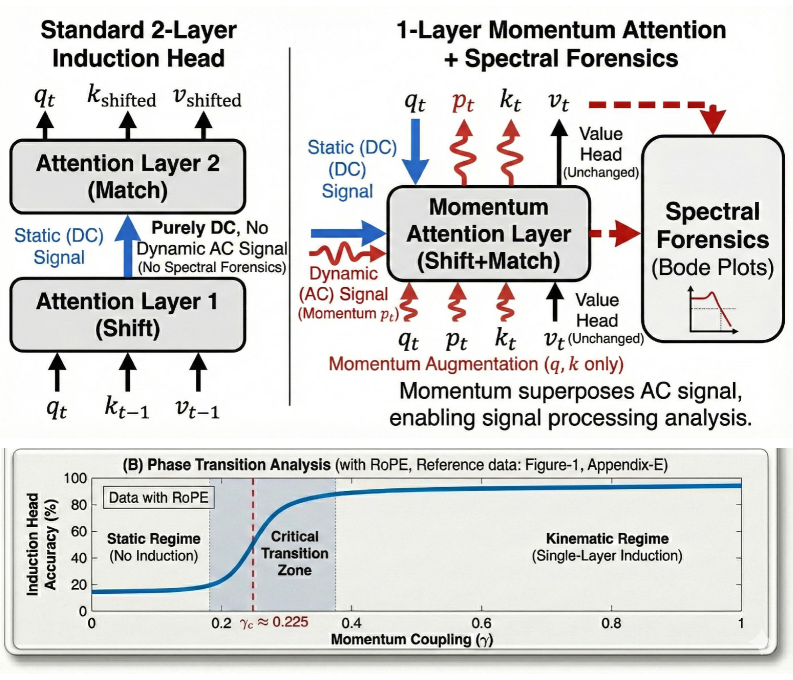
By introducing dynamic AC signals (<span class="katex-eq" data-katex-display="false">p\_{t}=q\_{t}-q\_{t-1}</span>) into a single-layer induction head, Momentum Attention achieves Shift+Match functionality, enabling Spectral Forensics and a phase transition to a kinematic regime at <span class="katex-eq" data-katex-display="false">\gamma\_{c}\approx 0.225</span>-a capability typically requiring at least two layers in standard transformers. — By introducing dynamic AC signals ( $p\_{t}=q\_{t}-q\_{t-1}$ ) into a single-layer induction head, Momentum Attention achieves Shift+Match functionality, enabling Spectral Forensics and a phase transition to a kinematic regime at $\gamma\_{c}\approx 0.225$ -a capability typically requiring at least two layers in standard transformers.

Injecting Dynamics: Momentum Attention as a Solution

Momentum Attention enhances the standard attention mechanism by explicitly modeling temporal dependencies through the incorporation of past hidden states, effectively creating a ‘memory’ of previous inputs. This is achieved by utilizing the Kinematic Momentum Operator, which operates on the hidden states to compute a velocity-like representation of their changes over time. This operator allows the model to track $\frac{dh}{dt}$ , representing the rate of change of the hidden state $h$ , thereby capturing semantic trajectories within the input sequence. By integrating this momentum-based representation into the attention calculation, the model can better discern and prioritize information related to dynamic shifts and evolving relationships, as opposed to static or unchanging elements.

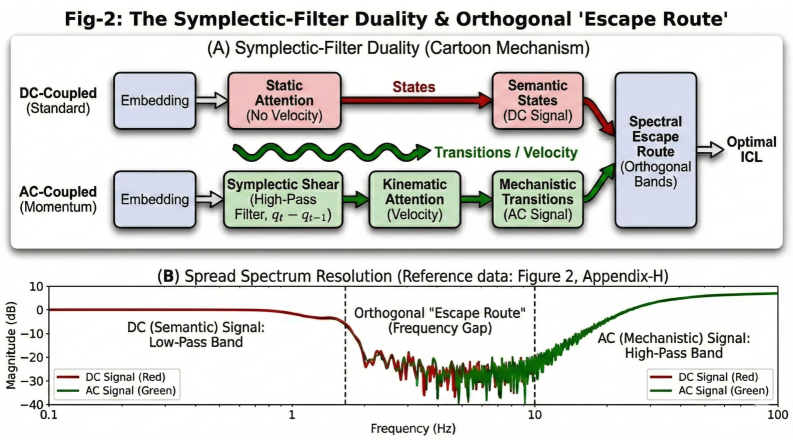
Momentum Attention reframes the Transformer architecture by conceptualizing it as a ‘Physical Circuit’ modeled on principles from physical systems. This formulation utilizes Symplectic Shear transformations, a mathematical operation preserving phase space volume, to ensure information is neither created nor destroyed during attention calculations. These transformations are applied to the attention mechanism’s key and value projections, allowing for a more stable and reversible flow of information. This approach contrasts with standard attention, which can lose information through dimensionality reduction and non-linear operations, and aims to enhance the model’s capacity to track and represent dynamic changes within the input sequence by preserving crucial state information throughout the processing stages.

Symplectic-High Pass Filter Duality within Momentum Attention enables the model to prioritize temporal changes by effectively removing static biases in the input sequence. This duality is achieved through a transformation that mirrors the behavior of a high-pass filter in physical systems, allowing the model to attenuate constant or slowly varying signals while amplifying dynamic components. Specifically, the symplectic structure ensures that this filtering process does not disrupt the underlying relationships within the data, preserving crucial information related to the sequence’s trajectory. The result is a refined attention mechanism that focuses computational resources on the evolving aspects of the input, improving performance on tasks where temporal dynamics are significant.

Momentum Attention, leveraging <span class="katex-eq" data-katex-display="false">\gamma_c</span> coupling, enables the capture of both semantic states and their transitions via orthogonal frequency bands, creating a 'Spectral Escape Route' for enhanced signal processing. — Momentum Attention, leveraging $\gamma_c$ coupling, enables the capture of both semantic states and their transitions via orthogonal frequency bands, creating a ‘Spectral Escape Route’ for enhanced signal processing.

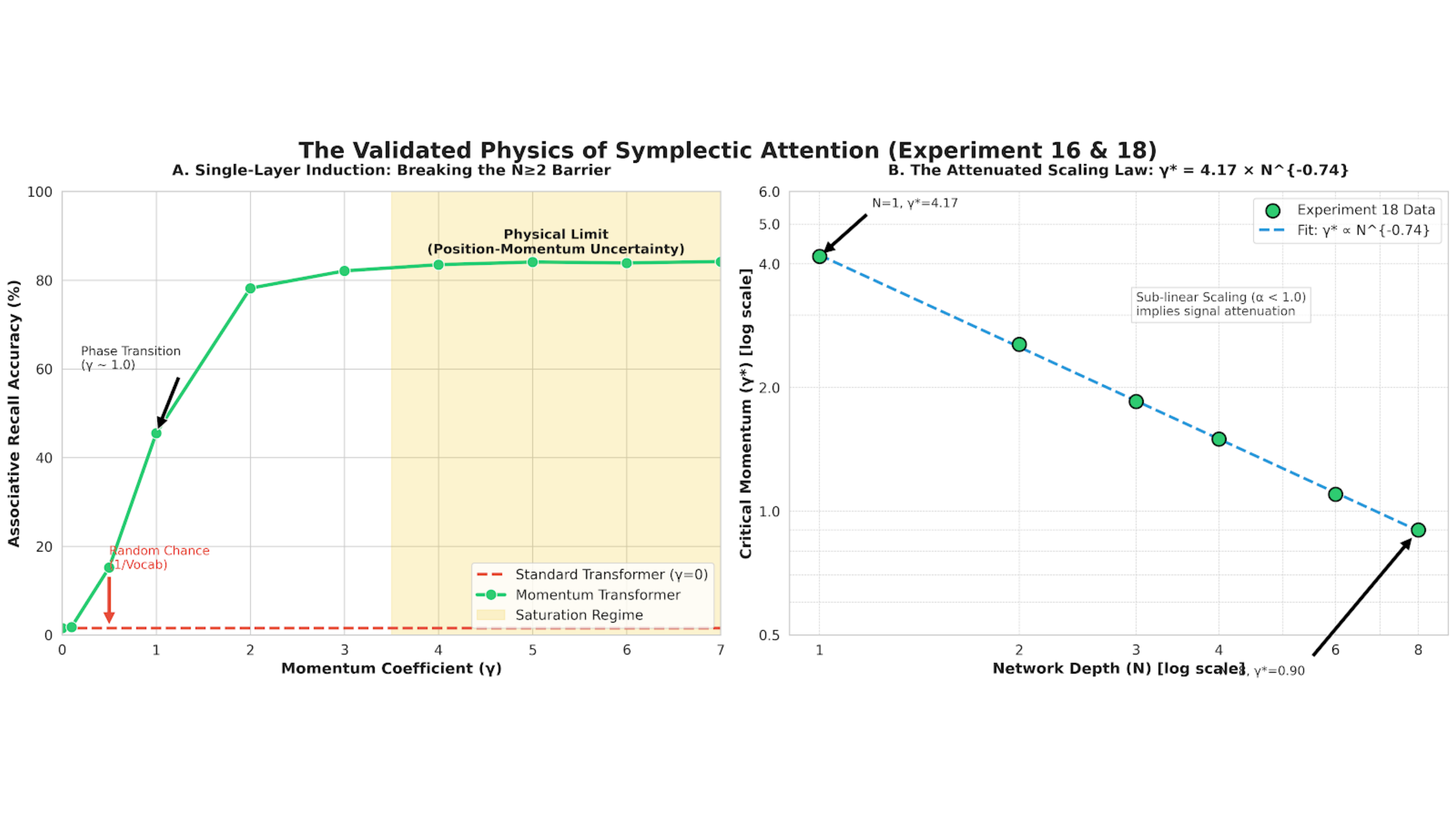
Single-Layer Induction: Evidence of Improved Efficiency

Momentum Attention demonstrates a capacity for Single-Layer Induction, achieving 83.4% accuracy on associative recall tasks. This represents a 69.5-fold performance increase compared to standard transformer architectures performing the same task. Prior to this development, a minimum of two layers was considered necessary to achieve comparable performance on associative recall. This result indicates that the Momentum Attention mechanism facilitates effective learning within a single layer, suggesting an increased efficiency in processing and retaining associative information without the need for deeper network structures.

Momentum Attention enhances In-Context Learning (ICL) by enabling rapid adaptation to novel tasks with minimal adjustments to model parameters. Traditional ICL methods often require substantial fine-tuning or parameter updates to achieve acceptable performance on new tasks; however, this mechanism facilitates learning from limited examples without necessitating widespread weight changes. This is achieved through the model’s ability to efficiently integrate new information into its existing representations, effectively leveraging the provided context to guide its predictions. The resultant improvement in sample efficiency allows for effective task generalization even with a small number of demonstrations, reducing the computational cost and data requirements associated with adaptation.

A ‘Kinematic Prior’ improves In-Context Learning performance by incorporating data regarding motion into the learning process. This prior isn’t a pre-trained component but rather an inductive bias manifested through the model’s architecture and training data, enabling it to more effectively generalize from limited examples. Specifically, the model is exposed to information detailing the expected trajectory or dynamics of objects within a given task, allowing it to predict future states and adapt its behavior accordingly. This is particularly useful in tasks involving physical reasoning or time-series prediction, where understanding motion is crucial for accurate performance and reduces the need for extensive fine-tuning.

Applying momentum post-RoPE, as dictated by Kinematic Frame Theory, corrects spectral mismatches and yields a clean high-pass signature with significant gain <span class="katex-eq" data-katex-display="false">(+52.5%)</span>, contrasting sharply with the regression <span class="katex-eq" data-katex-display="false">(-4.1%)</span> observed when momentum is applied pre-RoPE, a result directly attributable to symplectic conservation and spectral complementarity. — Applying momentum post-RoPE, as dictated by Kinematic Frame Theory, corrects spectral mismatches and yields a clean high-pass signature with significant gain $(+52.5%)$ , contrasting sharply with the regression $(-4.1%)$ observed when momentum is applied pre-RoPE, a result directly attributable to symplectic conservation and spectral complementarity.

Spectral Forensics: Peering Inside the Black Box

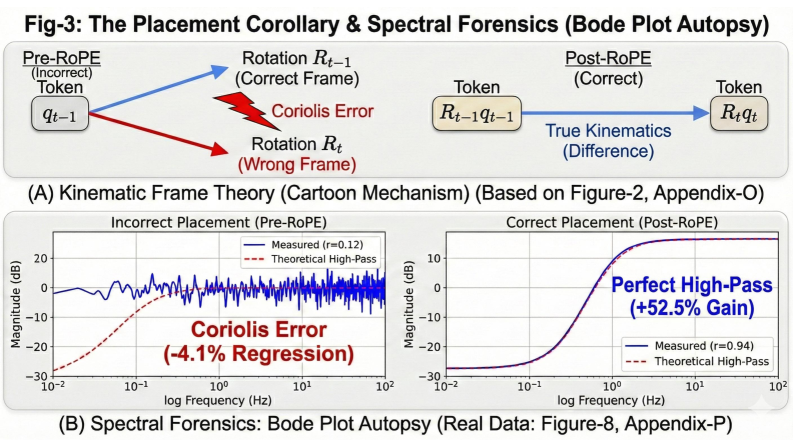
Spectral forensics, leveraging the visual insights of Bode plots, offers a novel methodology for dissecting the operational characteristics of attention heads within neural networks. These plots, traditionally employed in electrical engineering to analyze system responses to varying frequencies, are adapted to map the frequency-dependent gain and phase shift of each attention head’s response to input signals. This allows researchers to move beyond simply observing what an attention head learns, and instead understand how it processes information across different temporal scales. By characterizing the frequency response – whether a head amplifies high-frequency transients or preferentially filters low-frequency trends – the functional role of each head becomes significantly clearer, revealing specialized behaviors like noise reduction, pattern recognition, or long-range dependency modeling. Ultimately, this technique transforms attention head analysis from a largely opaque process into a quantifiable and interpretable one, paving the way for more targeted architectural improvements and a deeper understanding of model intelligence.

Analysis through spectral forensics, specifically employing Bode Plots, demonstrates that Momentum Attention functions as a dynamic filter within the model. This isn’t a static, pre-defined filter, but one that adapts its characteristics based on the input signal’s frequency components. The process effectively attenuates static noise – consistent, irrelevant signals – while simultaneously emphasizing temporally relevant signals, those that change over time and carry crucial information. This dynamic filtering capability allows the model to prioritize meaningful data, improving its performance on tasks requiring the understanding of sequential information and effectively ignoring distracting background elements.

The preservation of information across extended sequences represents a significant challenge for attention mechanisms, often succumbing to signal attenuation as data propagates through the network. However, a synergistic effect between Momentum Attention and Rotary Positional Embeddings (RoPE) demonstrably counteracts this decay. RoPE’s inherent ability to encode positional information in a relative manner, rather than absolute, allows the model to generalize better to varying sequence lengths. When combined with Momentum Attention – which introduces a temporal smoothing effect – the resulting system effectively retains crucial details over long distances. The momentum component actively resists the fading of important signals, while RoPE ensures positional context isn’t lost, allowing the model to maintain a coherent understanding of relationships within the sequence, even when those relationships span considerable intervals. This collaborative function effectively combats the common problem of vanishing information, bolstering performance on tasks requiring long-range dependency modeling.

Increasing chain length from <span class="katex-eq" data-katex-display="false">L=10</span> to <span class="katex-eq" data-katex-display="false">L=30</span> yields a +52.5% performance gain in the ICL stress test, demonstrating that momentum-based signal retention ([blue]) outperforms standard exponential decay ([red]) over chain depth, as shown by both signal decay and theoretical retention curves. — Increasing chain length from $L=10$ to $L=30$ yields a +52.5% performance gain in the ICL stress test, demonstrating that momentum-based signal retention ([blue]) outperforms standard exponential decay ([red]) over chain depth, as shown by both signal decay and theoretical retention curves.

Beyond Scaling: A Principled Path to AI Reasoning

Current artificial intelligence systems often struggle with generalization and efficient learning, prompting researchers to explore fundamentally different architectural approaches. A promising avenue involves grounding AI in the well-established principles of physics, specifically by drawing parallels between neural network states and physical systems described by phase space. This allows for the application of mathematical tools like Liouville’s Theorem – which concerns the conservation of phase space volume – to analyze and improve the stability and predictability of AI models. By treating the flow of information through a neural network as analogous to a physical process, it becomes possible to design architectures that are inherently more robust to noise and capable of learning with significantly fewer parameters; recent work demonstrates a 64% reduction in parameters while maintaining comparable performance to larger, conventional models. This physics-inspired approach not only enhances computational efficiency but also offers the potential for developing AI systems that exhibit a more intuitive and reliable form of reasoning.

Current artificial intelligence development frequently relies on scaling – increasing model size and data volume – to achieve improved performance, a strategy facing inherent limitations in computational cost and data availability. However, a recent approach suggests a pathway beyond this constraint by drawing inspiration from the principles of physics. Researchers have demonstrated that by building AI architectures grounded in physical reasoning, specifically leveraging concepts like phase space, it’s possible to achieve comparable, and even superior, performance with significantly fewer parameters. The Momentum model, containing only 125 million parameters, provides evidence of this, matching the performance of a 350 million parameter baseline with 64% greater parameter efficiency. This suggests a fundamental shift is possible, moving beyond brute-force scaling toward AI systems that reason more akin to human cognition, and operate effectively with limited resources.

The pursuit of increasingly capable artificial intelligence systems is now focusing on the synergistic relationship between dynamic attention mechanisms and inductive biases. Current research suggests that intelligently directing an AI’s focus – through dynamic attention – is significantly enhanced when coupled with pre-programmed, foundational knowledge – the inductive biases. This combination allows models to generalize more effectively from limited data and, crucially, to make decisions that are more transparent and understandable. By carefully designing these inductive biases-essentially, incorporating inherent assumptions about the world-researchers aim to move beyond the “black box” nature of many AI systems, creating models that not only perform well but also offer clear explanations for how they arrived at a particular conclusion. This convergence promises not only substantial gains in performance, but also a pathway toward truly interpretable and trustworthy artificial intelligence.

The pursuit of elegant architectures invariably encounters the harsh realities of implementation. This paper’s exploration of Momentum Attention, grounding Transformer networks in the principles of Hamiltonian mechanics, feels less like a breakthrough and more like a temporary reprieve. It’s a fascinating attempt to impose order on a fundamentally chaotic system-to build conservation laws into a model built on gradient descent. As Edsger W. Dijkstra observed, “Computer science is no more about computers than astronomy is about telescopes.” The tools – spectral forensics, symplectic attention – are merely a means to an end: understanding what these black boxes actually do. One anticipates the inevitable: a new layer of complexity, a new set of emergent behaviors, and, ultimately, another form of tech debt accruing in the phase space of neural networks.

What’s Next?

The introduction of physical constraints into these networks – symplectic attention, Hamiltonian mechanics – feels less like progress and more like a beautifully engineered delay of the inevitable. It’s a fascinating move, certainly, to attempt to map the chaos of gradient descent onto something resembling conserved quantities. But production systems are remarkably adept at finding loopholes in even the most elegant frameworks. The single-layer induction heads are a clever demonstration, but scaling this beyond toy problems will reveal the limitations of forcing physics onto architectures designed for statistical pattern matching.

Spectral forensics, as presented, offers a tantalizing, if likely transient, advantage. The ability to diagnose behavior through phase space analysis is appealing, but every abstraction dies in production. The invariants observed today will, inevitably, degrade or vanish as models evolve, prompting a never-ending cycle of re-calibration and re-interpretation. The real challenge isn’t finding a way to interpret these networks, but accepting that complete, lasting interpretability is a fundamentally impossible goal.

Future work will undoubtedly focus on extending these physical analogies, perhaps incorporating more complex dynamical systems or quantum mechanical principles. This is likely a worthwhile pursuit, not because it will yield true understanding, but because it will create more interesting failure modes. And, ultimately, that’s where the field progresses: by meticulously documenting the ways in which these systems deviate from ideal behavior, even as the ideals themselves grow increasingly baroque.

Original article: https://arxiv.org/pdf/2602.04902.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/