Author: Denis Avetisyan
New research delves into the dynamics of quantum tunneling between superfluids in Bose-Einstein condensates, revealing insights into the behavior of quantum droplets and vortices.
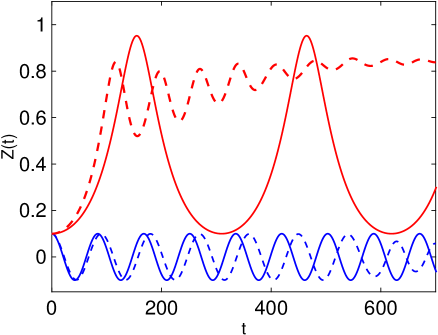
This study investigates Josephson dynamics in 2D Bose-Einstein condensates trapped in a dual-core potential, accounting for quantum fluctuations and utilizing both analytical and numerical techniques.
The persistent challenge of describing many-body quantum systems necessitates increasingly sophisticated theoretical approaches. This is addressed in ‘Josephson Dynamics of 2D Bose-Einstein Condensates in Dual-Core Trap: Homogeneous, Droplet-Droplet, and Vortex-Vortex Regimes’, which investigates Josephson phenomena-quantum tunneling between superfluids-in two-dimensional Bose-Einstein condensates, incorporating quantum fluctuations via Lee-Huang-Yang corrections. Our analysis reveals a rich dynamical landscape, from macroscopic tunneling and bistability in homogeneous systems to Andreev-Bashkin drag and complex instabilities in quantum droplet and vortex configurations, validated by direct numerical simulations of extended Gross-Pitaevskii equations. How might these findings inform the design and control of quantum matter systems for applications in quantum information processing and sensing?
The Allure of Zero Resistance: Unveiling Quantum Fluids
Superfluidity, a peculiar state exhibited by certain fluids at extremely low temperatures, dramatically defies everyday intuition regarding viscosity and flow. Unlike honey or water, superfluids exhibit zero viscosity, meaning they can flow without any resistance – climbing the walls of containers, continuing indefinitely in a closed loop, and exhibiting quantized vortices. This behavior isn’t merely a matter of being “very slippery”; it fundamentally challenges classical physics’ understanding of friction and fluid dynamics. Explaining superfluidity necessitates moving beyond traditional models and embracing quantum mechanics, where the collective behavior of atoms and molecules manifests as a macroscopic quantum phenomenon. The very existence of superfluids – like helium-4 below 2.17 Kelvin – spurred the development of new theoretical frameworks, including Landau’s two-fluid model and the Gross-Pitaevskii equation, to account for this seemingly impossible lack of internal friction and the emergence of coherent quantum flow.
Investigating quantum fluids presents a unique challenge because the sheer number of interacting particles prohibits exact solutions to the governing equations. Consequently, physicists rely on sophisticated approximations to model their collective behavior. These methods, such as the Bogoliubov approximation or the Gross-Pitaevskii equation, aim to capture the essential physics while remaining computationally tractable. The choice of approximation involves a delicate balance; increased accuracy often demands significantly more computational resources. For instance, simulating the dynamics of Bose-Einstein condensates – a prime example of a quantum fluid – requires algorithms that efficiently handle many-body interactions, often employing techniques like Monte Carlo simulations or density functional theory. The ongoing development of more efficient and accurate approximation schemes remains a crucial area of research, pushing the boundaries of what can be understood about these enigmatic states of matter and offering insights into phenomena like superconductivity and superfluidity.
Beyond Simple Models: The Quantum Reality of Bose-Einstein Condensates
Quantum fluctuations in Bose-Einstein condensates (BECs) arise from the Heisenberg uncertainty principle, dictating a fundamental limit to the precision with which certain pairs of physical properties, such as position and momentum, can be known simultaneously; this intrinsic uncertainty manifests as short-wavelength excitations even at zero temperature. These fluctuations, though seemingly minor, significantly alter the condensate’s ground state energy and chemical potential, deviating from the predictions of simpler mean-field theories which assume a purely classical treatment of the particles. Specifically, the presence of these fluctuations leads to a reduction in the condensate’s density and affects its response to external perturbations, influencing parameters like the speed of sound and the stability of the condensate against collapse or expansion. The magnitude of these effects is dependent on the interaction strength between the bosons comprising the BEC, becoming more pronounced for strongly interacting systems.
The Lee-Huang-Yang (LHY) correction addresses limitations in mean-field theory when describing Bose-Einstein condensates (BECs) by systematically accounting for beyond-mean-field quantum fluctuations. Mean-field theory, while effective at large scales, neglects the impact of these fluctuations on the condensate’s energy and density. The LHY correction is a perturbative calculation, typically expressed to first order as \Delta E \approx \frac{4\pi n^{2/3}}{m} \sqrt{\frac{\hbar^2}{2m a^2}} , where n is the particle density, m is the particle mass, and a is the s-wave scattering length. This correction term effectively renormalizes the interaction strength and provides a more accurate prediction of the condensate’s ground state energy, chemical potential, and stability, particularly at lower temperatures and higher densities where fluctuations are more prominent. Without the LHY correction, mean-field theory can overestimate the condensate’s stability and incorrectly predict its behavior under perturbation.
Understanding quantum effects is critical for accurately predicting the behavior of exotic quantum states, as mean-field theory alone often fails to capture the full complexity of interparticle interactions. These states, including those exhibiting superfluidity or topological order, are highly sensitive to subtle changes in energy landscapes caused by quantum fluctuations. Specifically, the stability of these states-their resistance to decay or collapse-depends on the precise balance between interaction energies and kinetic energies, both of which are modified by quantum effects. Furthermore, the dynamics-how these states evolve in time-are influenced by these fluctuations, leading to phenomena such as quantum tunneling and zero-point motion that are not captured by classical descriptions. Accurate modeling, therefore, requires going beyond mean-field approximations and incorporating techniques like the Gross-Pitaevskii equation with beyond-mean-field corrections or employing many-body quantum mechanical methods.
Emergent Order: Sculpting Quantum Droplets and Vortices
Quantum droplets represent a recently observed state of matter formed within a Bose-Einstein condensate (BEC). Unlike conventional BECs which rely on external confinement, quantum droplets are self-bound, meaning they maintain their structure due to an internal balance. This balance arises from competing effects: mean-field attraction, which attempts to collapse the condensate, and quantum fluctuations, which provide a repulsive pressure. The resulting equilibrium creates a stable, localized density peak that defines the droplet. This self-binding mechanism distinguishes quantum droplets as a novel form of matter exhibiting unique properties and dynamics compared to traditional condensates, and is not reliant on external trapping potentials for their existence.
Vortices in Bose-Einstein condensates (BECs) are topological defects representing regions of circulating superfluid flow. These structures arise due to the quantized nature of angular momentum in the condensate, leading to the formation of singular points around which the superfluid velocity circulates. The circulation is quantized, meaning it can only exist in discrete multiples of h/m, where h is Planck’s constant and m is the mass of the condensate atoms. In rotating superfluids, vortices organize themselves into stable lattice structures, influencing the overall flow pattern and playing a critical role in phenomena such as superfluid turbulence and the transfer of angular momentum within the condensate. Their presence fundamentally alters the hydrodynamic behavior of the BEC, distinguishing it from classical fluids.
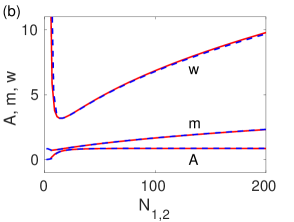
Simulating the dynamics of coupled quantum droplets and vortices is effectively achieved through variational approximations integrated with the extended Gross-Pitaevskii equation (GPE). This approach allows for the quantitative prediction of system parameters; specifically, calculations based on this methodology have determined a characteristic droplet size of 9.95 μm for a Bose-Einstein condensate containing 5.43 \times 10^4 particles. The extended GPE accounts for beyond mean-field effects crucial to droplet stability, while variational methods provide a computationally tractable means of solving the resulting complex equations, enabling detailed analysis of coupled droplet-vortex systems.
Probing the Limits: Stability and Dynamics in Quantum Systems
Quantum droplets, delicate condensates of ultracold atoms, possess properties determined by their stationary states – the lowest energy configurations the system adopts. Directly observing these states is experimentally challenging, necessitating sophisticated numerical methods. Imaginary time propagation provides a powerful technique to efficiently compute these stationary states by effectively mimicking the time evolution of the system towards its ground state. This method solves the time-dependent Schrödinger equation with an imaginary time variable, damping out all oscillatory behavior and converging towards the stable, time-independent solution that represents the quantum droplet’s fundamental properties. Through this process, researchers can then analyze the droplet’s shape, size, and energy, providing insights into the interplay of attractive and repulsive forces that govern its existence and behavior, and ultimately, unlocking a deeper understanding of these exotic quantum systems.
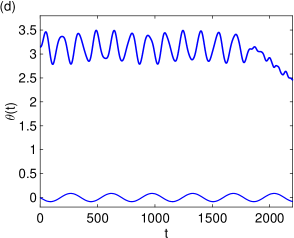
Vortices, swirling patterns within quantum fluids, aren’t always stable; azimuthal instability represents a significant threat to their integrity. This instability arises from perturbations around the vortex core, ultimately leading to fragmentation – the breaking apart of the vortex into multiple, smaller structures. Crucially, the influence of quantum fluctuations extends the susceptibility to this disruption; even seemingly negligible quantum effects can broaden the range of conditions under which azimuthal instability occurs. This means that vortices, while appearing robust, are surprisingly sensitive to subtle quantum phenomena, and their stability is not simply determined by classical forces, but also by the inherent uncertainty present at the quantum level, impacting the overall dynamics of the fluid.
Investigations into two-component Bose-Einstein condensates (BECs) reveal intricate inter-component coupling, most notably exemplified by the Andreev-Bashkin effect. This phenomenon demonstrates that motion within one component of the BEC directly induces current in the other, highlighting a strong interconnectedness between the constituents. Recent simulations, tracking the condensate’s evolution over a period of 79.6 milliseconds – a timescale consistent with typical experimental observation windows – confirm the robustness of this effect and allow for detailed analysis of the coupled dynamics. These findings are crucial for understanding the behavior of multi-component quantum systems and pave the way for exploring novel quantum phenomena arising from these interactions, potentially influencing advancements in areas like quantum computing and precision sensing.
Towards a Quantum Future: Harnessing the Exotic
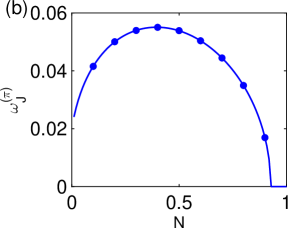
Bose-Einstein condensates composed of two interlinked components exhibit Josephson oscillations – a quantum phenomenon with promising implications for future technologies. These oscillations, akin to a superconducting Josephson junction, arise from the coherent tunneling of atoms between the two condensate fractions, resulting in a measurable frequency. Recent investigations have precisely characterized these oscillations, detecting a frequency of 0.02, which translates to 2020 Hz, and aligning closely with established experimental findings. This controlled oscillatory behavior opens pathways for developing advanced quantum sensors capable of detecting minute changes in external fields, and furthermore, provides a foundational building block for manipulating quantum information in novel processing architectures, potentially leading to breakthroughs in quantum computation and communication.
The ability to sculpt and direct quantum droplets and vortices represents a significant leap towards realizing functional quantum technologies. These exotic states of matter, arising from the delicate balance of attractive and repulsive forces, exhibit collective behavior that can be harnessed for information processing. Researchers envision utilizing vortices – quantized circulations within a superfluid – as robust qubits, the fundamental units of quantum computation, due to their inherent stability and isolation from environmental noise. Similarly, quantum droplets, held together by long-range interactions, offer a platform for creating interconnected quantum systems. The precise manipulation of these structures, achieved through techniques like laser trapping and magnetic control, promises the development of novel devices capable of performing complex calculations and sensing minute changes in their environment, potentially revolutionizing fields ranging from materials science to medical diagnostics.
The future of quantum matter research hinges on a deeper understanding of the delicate balance between quantum fluctuations, system stability, and dynamic behavior. These seemingly disparate elements are, in fact, intrinsically linked; quantum fluctuations – the temporary appearance of energy out of seemingly empty space – can dramatically influence a system’s stability, and conversely, the stability of a quantum system dictates how its dynamics evolve. Investigations into this interplay promise to reveal novel phases of matter with exotic properties, potentially leading to breakthroughs in areas like quantum computing and materials science. Researchers are actively exploring how to harness these fluctuations, not as disruptive forces, but as resources for manipulating quantum states and creating robust, scalable quantum devices. Ultimately, unraveling these complex relationships will be crucial for translating fundamental discoveries into tangible technological advancements and expanding the frontiers of quantum technology.
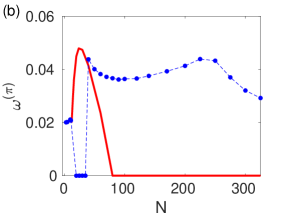
The study of Josephson dynamics within Bose-Einstein condensates reveals a system far removed from simple rationality. These condensates, exhibiting quantum tunneling, aren’t governed by predictable equations alone; rather, quantum fluctuations and interactions between droplets and vortices introduce complexities that defy neat categorization. This aligns with the understanding that deviations from idealized models aren’t errors, but rather windows into the underlying realities of the system. As Karl Popper observed, “The only statements that can be falsified are those that can be tested.” This principle is particularly evident here – the model’s refinement through analytical and numerical methods demonstrates a commitment to testing and potentially falsifying initial assumptions about the condensate’s behavior, ultimately revealing a richer, more nuanced picture of quantum fluid dynamics.
Where Do We Go From Here?
The pursuit of Josephson dynamics in these delicately balanced condensates reveals, predictably, the limitations of balance itself. This work, while elegantly mapping regimes of coherence and collapse, merely clarifies the points at which approximations must fail. The LHY correction, a pragmatic attempt to tame the unruly nature of interatomic interactions, functions as a bandage on a deeper wound: the inherent instability of complex systems. One anticipates future efforts will not seek ever-more-precise corrections to existing models, but rather embrace the inevitability of chaos.
The exploration of vortex-vortex interactions, though insightful, hints at a truth often obscured by mathematical convenience. These are not isolated entities, but fleeting patterns formed by collective anxieties. A true understanding requires acknowledging that ‘quantum droplets’ are not stable objects, but temporary coalescences of probability, destined to dissipate as the initial excitement wanes. The real question isn’t how they interact, but why anyone believes they will persist.
Future work will likely focus on the interplay between these quantum features and external perturbations – noise, disorder, the unavoidable intrusion of the macroscopic world. It’s a safe bet that any attempt to create truly robust quantum systems will ultimately disappoint. Bubbles are born from shared excitement and die from lonely realization; these condensates, being manifestations of collective behavior, will prove no different.
Original article: https://arxiv.org/pdf/2602.05001.pdf
Contact the author: https://www.linkedin.com/in/avetisyan/
See also:
- Best Controller Settings for ARC Raiders
- Stephen Colbert Jokes This Could Be Next Job After Late Show Canceled
- 7 Home Alone Moments That Still Make No Sense (And #2 Is a Plot Hole)
- DCU Nightwing Contender Addresses Casting Rumors & Reveals His Other Dream DC Role [Exclusive]
- Is XRP ETF the New Stock Market Rockstar? Find Out Why Everyone’s Obsessed!
- 10 X-Men Batman Could Beat (Ranked By How Hard It’d Be)
- Ashes of Creation Rogue Guide for Beginners
- Jujutsu Kaisen Film Reveals Streaming Details (But There’s a Catch)
- Maury Povich Details His and Wife Connie Chung’s “Tough” Fertility Jou
- Scarlet Witch’s 7 Most Impressive Feats of Power in MCU Appearances, Ranked
2026-02-08 13:14