The Limits of Quantum Distinction

Author: Denis Avetisyan

New research reveals a fundamental link between how well we can tell quantum states apart and the energy dissipated in the process.

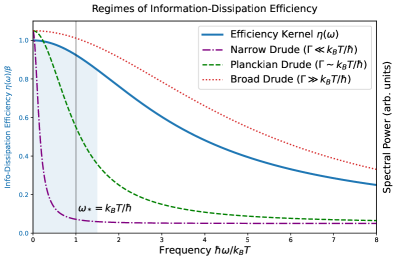
Information-dissipation efficiency is maximized within a specific spectral window-approximated by the Planckian regime-as systems concentrating spectral weight in this region achieve near-optimal performance, while those exhibiting significant high-frequency contributions demonstrate parametrically reduced efficiency, a relationship quantified by <span class="katex-eq" data-katex-display="false">\eta(\omega)/\beta</span> and illustrated through comparative analysis of Drude-like dissipation spectra. — Information-dissipation efficiency is maximized within a specific spectral window-approximated by the Planckian regime-as systems concentrating spectral weight in this region achieve near-optimal performance, while those exhibiting significant high-frequency contributions demonstrate parametrically reduced efficiency, a relationship quantified by $\eta(\omega)/\beta$ and illustrated through comparative analysis of Drude-like dissipation spectra.

A universal bound on state distinguishability is established, demonstrating optimal information-dissipation efficiency when dissipation concentrates at frequencies below the Planckian scale.

A fundamental challenge in understanding many-body quantum systems is determining the limits to how efficiently work can induce distinguishable changes in a system’s state. In this work, ‘Information, Dissipation, and Planckian Optimality’, we derive a universal bound on this efficiency, quantifying it through the quantum Fisher information and demonstrating its connection to dissipated work. This bound reveals an optimal regime where efficiency peaks when dissipation concentrates at frequencies below the Planckian scale $ω_\star \sim k_B T/\hbar$ , suggesting that systems like strange metals operate at the edge of this optimality. Could this framework provide a novel means of characterizing the interplay between dissipation and information in strongly correlated electronic systems, and ultimately, a deeper understanding of their emergent properties?

The Inevitable Cost of Computation

The fundamental link between energy dissipation and information processing defines the ultimate capabilities of complex systems. In many-body systems – those comprised of numerous interacting particles – energy loss isn’t merely a nuisance, but an inherent part of how information is encoded, transmitted, and ultimately, what computations are possible. Characterizing this dissipation is therefore crucial; it establishes a fundamental limit on how efficiently a system can process information, as any energy lost represents a potential loss of signal or computational capacity. Researchers are increasingly recognizing that understanding the precise mechanisms of dissipation – how energy flows from coherent computational states to environmental reservoirs – allows for the development of strategies to minimize these losses and, consequently, push the boundaries of information processing in realms like quantum computing and nanoscale devices. This connection highlights that optimizing performance isn’t simply about maximizing energy input, but intelligently managing its inevitable dissipation.

Conventional understandings of energy dissipation frequently characterize it as an entirely detrimental process, a simple loss of usable energy that degrades system performance. However, this perspective overlooks a crucial connection: dissipation isn’t solely destructive; it can be intrinsically linked to information gain. As a system dissipates energy, it effectively encodes information about its environment and its own internal state into the dissipated energy carriers. This encoding represents a fundamental trade-off; while energy is lost to perform computation or maintain a specific state, the resulting dissipation carries information that can be harnessed or utilized. Recognizing this duality is vital for accurately assessing the efficiency of complex systems, particularly in quantum technologies where dissipation often accompanies and influences non-equilibrium dynamics and potentially enables novel forms of information processing.

Viewing dissipation solely as a detrimental force significantly restricts the development of efficient quantum technologies. When a quantum system operates outside of equilibrium – a common scenario in computation and sensing – energy lost through dissipation isn’t simply wasted; it’s inextricably linked to the system’s ability to process information and evolve towards desired states. Traditional analytical tools, built on the assumption of purely destructive dissipation, fail to capture this nuanced relationship, hindering accurate quantification of system performance and the design of optimized control protocols. Consequently, efforts to enhance the efficiency of quantum devices are often misdirected, overlooking opportunities to harness dissipation as a resource for driving coherent dynamics and extracting useful work from non-equilibrium processes. A revised framework, acknowledging the constructive role of dissipation, is therefore crucial for unlocking the full potential of these advanced systems.

Quantifying the Efficiency of Dissipation

Information-Dissipation Efficiency (IDE) is defined as a quantitative metric assessing the capability of dissipative processes to generate distinguishable quantum states. Unlike traditional analyses focused on energy or entropy changes, IDE directly relates the amount of dissipation to the resulting state distinguishability. This framework posits that effective dissipation isn’t simply about reducing energy, but about creating readily identifiable quantum states, thereby enabling information processing. The metric is calculated by quantifying how well the final, dissipated state can be differentiated from its initial or equilibrium state, providing a direct link between thermodynamic processes and information content.

Quantifying the distance between non-equilibrium, driven states and the equilibrium state necessitates the application of a suitable metric; the Bures distance is utilized for this purpose due to its properties in describing the distinguishability of quantum states. Theoretical analysis demonstrates that this distance is bounded by $\le \beta/4 * W_{diss}$ , where β represents the inverse temperature and $W_{diss}$ denotes the work dissipated during the process. This bound establishes a direct relationship between the degree of distinguishability between states and the amount of dissipated work, providing a quantifiable link between thermodynamic and information-theoretic perspectives.

Traditional analysis of non-equilibrium systems has largely focused on thermodynamic quantities like heat and entropy production. However, framing dissipation – the irreversible conversion of energy – as fundamentally linked to the creation of distinguishable states shifts the analytical perspective towards information theory. This approach recognizes that dissipation isn’t merely energy loss, but a process that generates differences between system states, thereby encoding information. Consequently, quantifying dissipation through the lens of state distinguishability allows for the assessment of how effectively a system utilizes energy to create discernible configurations, moving beyond solely characterizing energy flow and towards understanding the informational consequences of irreversible processes. This facilitates the development of metrics, such as Information-Dissipation Efficiency, that directly relate energy dissipation to the capacity for information storage or processing within the system.

Linear Response and the Planckian Limit

Linear Response Theory (LRT) is a formal framework used to determine the response of a system to small, time-dependent perturbations. It establishes a direct relationship between the applied perturbation and the resulting change in a measurable physical quantity, effectively quantifying the system’s susceptibility. The core principle relies on expressing the response as a time-convolution of the perturbation with a response function – often a correlation function of the system’s intrinsic fluctuations – allowing for the calculation of dynamic properties from equilibrium statistical mechanics. This approach is particularly valuable because it bypasses the need to solve the full time-dependent Schrödinger equation for the perturbed system; instead, it leverages the established statistical behavior of the unperturbed system to predict its behavior under external influence. The theory is broadly applicable across diverse physical systems, from condensed matter physics to quantum optics, providing a rigorous method to analyze dissipative processes and understand how systems evolve away from equilibrium.

Investigations into systems operating near the ‘Planckian Scale’ demonstrate a specific energy frequency, denoted as $ω⋆$ , at which the efficiency of energy dissipation undergoes a transition. This characteristic frequency is mathematically defined as approximately $ω⋆ ~ k_BT/ħ$ , where $k_B$ represents the Boltzmann constant and $ħ$ is the reduced Planck constant. Below this frequency, dissipation is generally efficient, meaning perturbations are quickly absorbed and thermalized. Conversely, above $ω⋆$ , dissipation becomes markedly less efficient, indicating a reduced capacity for the system to absorb energy from external perturbations and maintain thermal equilibrium. This transition is not a sharp cutoff, but rather represents a change in the rate at which energy is dissipated, influencing the system’s response to time-dependent forces.

Kubo-Martin-Schwinger (KMS) relations provide a formal framework for calculating the linear response function of a system to external perturbations. Specifically, these relations express the time-dependent response of an observable $A(t)$ to a time-dependent perturbation $B(t)$ as an integral over the correlation function of $A(t)$ and $B(t)$ . This allows for the rigorous determination of dissipation rates, which are directly related to the imaginary part of the response function. The framework relies on the assumption of linear response – that the perturbation is sufficiently weak – and connects microscopic dynamics to macroscopic observables, offering a quantitative method for understanding how systems evolve under external influences and how energy is dissipated from those systems.

Strange Metals and the Limits of Conductivity

Recent investigations into ‘strange metals’ propose a paradigm shift in understanding their peculiar characteristics, moving beyond traditional condensed matter physics. These materials, exhibiting behavior drastically different from conventional metals, are now being analyzed through the framework of Information-Dissipation Efficiency and the $\hbar$ Planck constant. This approach posits that the rate at which information is lost – dissipated as heat – is fundamentally linked to the quantum mechanical limits imposed by the Planckian scale. Rather than focusing solely on electron interactions, this lens emphasizes how efficiently a material can process and ultimately dissipate information, offering a new perspective on phenomena like linear-in-temperature resistivity. By considering information as a physical quantity subject to thermodynamic constraints, researchers are gaining insight into the emergent properties of these materials and potentially unlocking pathways towards novel electronic devices with unprecedented capabilities.

Certain materials, termed ‘strange metals’, demonstrate profoundly unusual electrical and thermal properties when positioned close to ‘quantum critical points’ – specific temperatures or pressures where a material undergoes a phase transition. Unlike conventional metals governed by well-established theories, these materials exhibit a resistance that increases linearly with decreasing temperature, a behavior directly contradicting established models. Furthermore, the relationship between resistivity and temperature deviates significantly from predictions, and their thermal conductivity doesn’t align with expected behavior. This anomalous behavior isn’t simply a minor deviation; it represents a fundamental challenge to conventional condensed matter physics, suggesting that entirely new theoretical frameworks are required to accurately describe the physics at play and potentially unlock revolutionary technological applications.

The unusual characteristics of ‘strange metals’ are increasingly understood through the lens of dissipation efficiency, a principle suggesting an upper limit – denoted as $η(ω) \leq β$ – on how quickly these materials shed energy. This framework proposes that the unique properties observed in strange metals aren’t simply deviations from conventional physics, but rather a direct consequence of operating near this maximum dissipation bound. By approaching this limit, these materials exhibit behaviors like linear-in-temperature resistivity, challenging traditional models of metallic conductivity. Crucially, this understanding isn’t purely theoretical; the potential to control dissipation at this scale opens avenues for designing novel devices with unprecedented efficiency and responsiveness, potentially revolutionizing fields ranging from energy storage to quantum computing, as the precise management of energy loss becomes a key design parameter.

Beyond Limits: Precision and the Cost of Measurement

Thermodynamic Uncertainty Relations represent a profound shift in understanding the inherent limitations of measurement precision. These relations demonstrate that any attempt to determine a physical quantity with ever-increasing accuracy is fundamentally constrained by the entropy produced during the measurement process itself. Essentially, the more precisely one seeks to know a parameter, the more disturbance – and thus entropy – is generated, establishing a trade-off between knowledge gained and thermodynamic cost. This isn’t merely a practical limitation of instruments; it’s a consequence of the second law of thermodynamics applied to information acquisition. The degree of uncertainty in estimating a parameter is therefore inextricably linked to the dissipation of energy, quantified by the entropy production, implying that perfect precision is unattainable, and that any measurement will inevitably introduce some degree of disturbance to the system being observed. $\Delta x \Delta p \ge \frac{\hbar}{2}$

Quantum Fisher Information (QFI) serves as a crucial metric for evaluating the ultimate precision achievable in estimating parameters within a quantum system, offering a distinct perspective from traditional methods. Unlike classical approaches, QFI doesn’t simply assess how well one can distinguish between states; it quantifies the maximal amount of information a quantum state carries about an unknown parameter. Importantly, research demonstrates a direct connection between QFI and dissipation – the unavoidable loss of energy as heat – within the measurement process. A higher QFI typically implies a greater sensitivity to parameter changes, but also a potentially larger dissipation footprint, suggesting a fundamental trade-off. This link is not merely correlational; the very act of enhancing precision, as quantified by QFI, often necessitates increasing the system’s interaction with its environment, thereby amplifying dissipative effects and establishing a key constraint on the limits of quantum metrology and sensing.

Recent theoretical advances suggest a pathway to surpass fundamental limits on measurement precision by optimizing what is known as Information-Dissipation Efficiency. This principle, grounded in a universal bound linking the distinguishability of quantum states to the work dissipated during a measurement, proposes that maximizing the information gained relative to the energy expended can unlock enhanced sensing and computational capabilities. Essentially, systems designed to extract the most signal while minimizing energy loss demonstrate superior performance; this is particularly relevant in scenarios where thermodynamic uncertainty relations traditionally impose constraints. By carefully engineering quantum systems to achieve high Information-Dissipation Efficiency, researchers aim to develop sensors capable of detecting incredibly weak signals and quantum computers less susceptible to errors, potentially revolutionizing fields ranging from materials science to medical diagnostics.

The pursuit of optimal efficiency, as demonstrated by this work concerning information-dissipation efficiency, echoes a fundamental tenet of rational inquiry. This paper rigorously establishes a bound on the distinguishability of quantum states, linking it directly to dissipated work – a clear message that an error isn’t a failure, but a signal. It’s a verification of the inherent limits on information processing, reaching optimal performance when dissipation concentrates at lower frequencies. As John Locke observed, “All knowledge is ultimately based on perception.” Here, perception translates to measurable distinctions between quantum states, limited by the unavoidable dissipation inherent in any physical process. The study doesn’t prove an ideal; it defines the boundary within which improvement is possible, aligning with the principle that truth emerges from repeated attempts to disprove a model.

What’s Next?

The demonstration of a universal bound connecting state distinguishability to dissipated work is, predictably, not a final statement. It is, rather, a precise articulation of where intuition falters. The observation that Planckian dissipation optimizes information processing isn’t surprising – nature rarely favors extravagance – but the rigorous quantification invites scrutiny. Anything confirming expectations needs a second look. Future work must address the limitations inherent in defining ‘work’ within complex, many-body systems; the Kubo-Martin-Schwinger framework, while powerful, isn’t immune to interpretive ambiguity.

A more pressing question concerns the relevance of the Planckian scale itself. Is this a fundamental constraint, or merely an artifact of the approximations employed? Exploring deviations from Planckian dissipation – whether through engineered systems or the discovery of exotic materials – will be crucial. The Bures distance, used here as a measure of distinguishability, isn’t the only metric available; alternative measures might reveal different, and potentially more nuanced, bounds.

Ultimately, this work reinforces a simple principle: a hypothesis isn’t belief – it’s structured doubt. The true value lies not in establishing a ‘law,’ but in defining the precise conditions under which that law fails. The search for exceptions – for systems that demonstrably outperform Planckian optimality – will be the most fruitful avenue for future investigation.

Original article: https://arxiv.org/pdf/2602.04953.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/