Weaving Spacetime from Matter

Author: Denis Avetisyan

A new approach to loop quantum gravity proposes that spacetime itself emerges directly from the interactions of matter fields.

The transformation of a quantum bit from one block configuration to another yields either a <span class="katex-eq" data-katex-display="false">(M+1)(M+1)</span> or <span class="katex-eq" data-katex-display="false">(M-1)(M-1)</span> block, a dynamic echoing the fundamental instability inherent in any theoretical construct-a principle first outlined by Penrose in 1971. — The transformation of a quantum bit from one block configuration to another yields either a $(M+1)(M+1)$ or $(M-1)(M-1)$ block, a dynamic echoing the fundamental instability inherent in any theoretical construct-a principle first outlined by Penrose in 1971.

This review details a construction of combinatorial spacetime from matter fields, leveraging spin networks and the tetrad formalism to potentially reconcile general relativity and quantum mechanics.

Reconciling general relativity and quantum mechanics remains a central challenge in theoretical physics, particularly regarding the fundamental nature of spacetime itself. The paper ‘Combinatorial Spacetime from Loop Quantum Gravity’ addresses this by reformulating loop quantum gravity-a promising candidate for quantum gravity-solely in terms of matter fields, moving away from a spacetime-first approach. This construction, inspired by Penrose’s ideas, posits that spacetime emerges from the relationships between these fields, with curvature arising from the vertices of an underlying combinatorial structure. Could this purely relational framework offer a resolution to the conceptual difficulties inherent in defining spacetime within a quantum theory of gravity and unlock a deeper understanding of the universe’s fundamental building blocks?

The Illusion of a Unified Cosmos

The pursuit of a complete understanding of the universe is currently stymied by a fundamental discord between two pillars of modern physics: General Relativity and Quantum Mechanics. General Relativity elegantly describes gravity as the curvature of spacetime, excelling at predicting phenomena on cosmic scales, like the orbits of planets and the behavior of black holes. However, this framework breaks down when applied to the incredibly small scales governed by Quantum Mechanics, which dictates the behavior of particles at the atomic and subatomic levels. Quantum Mechanics, while remarkably accurate in its domain, doesn’t naturally accommodate gravity, leading to mathematical inconsistencies and nonsensical predictions when attempts are made to merge the two. This incompatibility isn’t merely a mathematical inconvenience; it suggests that a crucial element is missing from our understanding of the universe-a more fundamental theory capable of unifying these seemingly disparate realms and providing a consistent description of reality from the smallest particles to the largest cosmic structures.

Despite decades of research, attempts to reconcile General Relativity and Quantum Mechanics through frameworks like String Theory have encountered significant hurdles. While mathematically elegant, String Theory postulates the existence of extra spatial dimensions and requires energy scales far beyond current experimental capabilities, hindering empirical verification. This lack of testability, coupled with the theory’s inherent complexities – including the vast “landscape” of possible solutions – has motivated physicists to explore alternative avenues for unification. These approaches range from Loop Quantum Gravity, which quantizes spacetime itself, to investigations into emergent gravity, where gravity isn’t a fundamental force but arises from underlying microscopic degrees of freedom, all driven by the need for a framework grounded in observable phenomena and predictive power.

The persistent challenge of reconciling General Relativity and Quantum Mechanics suggests that spacetime, traditionally conceived as a smooth, continuous fabric, may possess a fundamentally discrete structure at the Planck scale. Current theoretical frameworks struggle to describe gravity at the quantum level, potentially because they rely on this continuous model where infinities and inconsistencies arise. Researchers are now exploring models where spacetime is ‘quantized’ – composed of discrete units rather than infinitely divisible points – analogous to how matter is composed of atoms. These approaches, including loop quantum gravity and causal set theory, propose that spacetime emerges from more fundamental, discrete building blocks, potentially resolving the singularities predicted by General Relativity and offering a pathway towards a unified theory. Understanding this granular nature of spacetime – if it exists – could redefine our understanding of gravity, the universe’s origins, and the very nature of reality.

The Geometry of Spacetime: A Mathematical Mirror

General Relativity mathematically describes gravity not as a force, but as a manifestation of the curvature of spacetime, determined by the distribution of mass and energy. This description is formalized using the concept of diffeomorphisms – smooth, invertible transformations of spacetime coordinates – which ensure that physical laws remain consistent regardless of coordinate choice. The dynamics of this curvature are governed by the Einstein-Hilbert Action, a functional expressed as an integral of the Ricci scalar $R$ over spacetime, represented as $S = \in t d^4x \sqrt{-g} R$ , where $g$ is the determinant of the metric tensor.

The Einstein-Hilbert Action, central to General Relativity, is mathematically expressed as an integral of the Ricci scalar $R$ over spacetime, multiplied by a constant related to the gravitational constant and Planck’s constant. This action describes the dynamics of spacetime itself, with variations in the action leading to the Einstein field equations. Crucially, the action also incorporates the Cosmological Constant, Λ, which represents the energy density of the vacuum of space. This term allows for solutions describing an expanding or contracting universe, and effectively modifies the gravitational field equations to account for the intrinsic energy present even in the absence of matter or radiation. The complete action is therefore written as $S = \in t d^4x \sqrt{-g} (R - 2\Lambda)$ , where $g$ is the determinant of the metric tensor.

Tetrads, also known as vierbeins, provide a means of relating the curved spacetime manifold of General Relativity to a flat, local Minkowski space at each point, facilitating calculations by allowing the use of flat-space coordinates; mathematically, a tetrad $e^a_{\mu}$ transforms vectors between the curved spacetime index μ and the flat, local Lorentz index $a$ . Ashtekar Connections, developed by Abhay Ashtekar, reformulate General Relativity as a gauge theory similar to Yang-Mills theory by expressing the gravitational field as a connection on a principal bundle; specifically, this involves representing the metric in terms of the triad and the connection, resulting in a first-order formalism where the gravitational field equations are expressed as equations analogous to those found in other gauge theories, simplifying quantization efforts and enabling the application of techniques from particle physics.

A 3D manifold is discretized into tetrahedra, represented by a triangulation graph Γ of edges and vertices, and its dual graph <span class="katex-eq" data-katex-display="false">\tilde{\Gamma}</span> connects the centers of these tetrahedra. — A 3D manifold is discretized into tetrahedra, represented by a triangulation graph Γ of edges and vertices, and its dual graph $\tilde{\Gamma}$ connects the centers of these tetrahedra.

Weaving the Fabric: Spin Networks and Quantum Spacetime

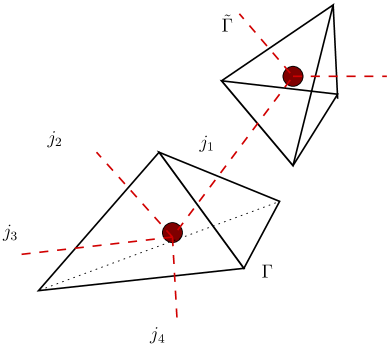
Loop Quantum Gravity (LQG) proposes that spacetime is not continuous, but rather quantized – meaning it possesses a discrete, granular structure at the Planck scale. This quantization is achieved by constructing spacetime from fundamental building blocks called spin networks. These networks are graphs where edges represent quantized units of area and nodes represent quantized volumes. The geometry of spacetime, therefore, is encoded in the relationships between these nodes and edges, effectively replacing the smooth manifold of General Relativity with a discrete, combinatorial structure. This approach differs from String Theory, which quantizes gravity via extended objects, and offers a background-independent quantization of spacetime, meaning it does not rely on a pre-existing spacetime geometry.

The Holonomy Operator in Loop Quantum Gravity (LQG) describes how a quantum state changes after being parallel-transported around a closed loop. This operator, derived from the Ashtekar connection, effectively measures the curvature of spacetime at the Planck scale – approximately $10^{-{35}}$ meters. Crucially, the eigenvalues of the Holonomy Operator are discrete, not continuous, indicating that spacetime geometry is quantized. This quantization results in a granular structure where areas and volumes can only take on specific, discrete values, fundamentally challenging the classical notion of a smooth, continuous spacetime. The discrete spectra of these operators provide evidence for the fundamental discreteness of spacetime within the LQG framework.

The Ashtekar connection, introduced in 1987, reformulated General Relativity in a way amenable to the techniques of gauge theory used in quantum field theory. This reformulation achieves this by expressing the gravitational field not in terms of the metric tensor $g_{\mu\nu}$ , but instead using a connection variable $A^i_a$ and its conjugate momentum $E^a_i$ . Crucially, these variables satisfy the same algebraic relations as the gauge fields and their conjugate momenta in Yang-Mills theory, allowing the quantization procedures developed for Yang-Mills to be applied to gravity. This transformation is not merely a change of variables; it reveals a previously hidden symmetry in General Relativity, making it suitable for canonical quantization within the Loop Quantum Gravity framework, and ultimately facilitating the construction of spin networks as the fundamental quanta of spacetime.

Discretizing a continuous Lagrangian framework is achieved by introducing a set of vertices to a free loop.

Beyond Points and Lines: Matter Networks and the Emergent Universe

Matter spin networks offer a novel framework for understanding the deep connection between the quantum fabric of spacetime and the interactions of fundamental particles. These networks are constructed directly from matter fields, effectively weaving spacetime geometry from the very substance of particle existence. The resulting structure provides a visual and mathematical link to Feynman diagrams, those familiar tools used to depict particle interactions; each diagram can be interpreted as a specific configuration within the matter spin network. This correspondence suggests that spacetime isn’t merely a backdrop for particle interactions, but is actively built by them, offering a potential resolution to long-standing questions about the nature of quantum gravity and the emergence of spacetime itself. By grounding spacetime in the dynamics of matter, this approach moves beyond traditional perturbation theories and opens avenues for exploring quantum gravity in a fundamentally new way.

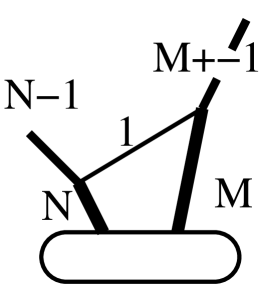
Penrose’s Combinatorial Spacetime challenges the conventional understanding of spacetime as a smooth, continuous entity, proposing instead a fundamentally discrete structure built entirely from the arrangement of matter. This approach diverges from traditional models by asserting that spacetime isn’t a pre-existing backdrop for physical events, but rather emerges from the relationships between material constituents. The current work advances this concept by explicitly constructing spacetime solely in terms of matter fields, effectively reversing the typical dependency. Rather than locating particles within spacetime, this framework defines spacetime through the network of interactions between these fields, suggesting a universe where the very fabric of reality is a consequence of material organization. This discrete construction offers a potential pathway to reconcile quantum mechanics and general relativity, as it naturally incorporates the quantization of geometry at a fundamental level, and avoids the singularities often predicted by continuous spacetime models.

The complex interplay of matter and spacetime, as modeled through matter networks, ultimately manifests as a simplified, yet revealing, 2-dimensional universe. This ‘toy universe’ isn’t an arbitrary simplification; it’s mathematically equivalent to the boundary of a 3-dimensional simplex – a fundamental geometric shape akin to a tetrahedron. By representing spacetime in this way, researchers can explore the fundamental relationship between matter and geometry without the complexities of higher dimensions. This approach allows for focused calculations and visualizations, offering a powerful tool for understanding how the very fabric of spacetime emerges from the interactions of matter fields and, crucially, providing a concrete framework to test the predictions of combinatorial spacetime against known physics.

The renormalization procedure fuses two spin-<span class="katex-eq" data-katex-display="false">\frac{1}{2}</span> fermions into a spin-1 boson vertex within a matter spin network. — The renormalization procedure fuses two spin- $\frac{1}{2}$ fermions into a spin-1 boson vertex within a matter spin network.

The Horizon of Understanding: Towards a Unified Theory

Current investigations are actively probing how these theoretical frameworks reshape understandings of the universe’s origins and ultimate fate. Researchers are utilizing these models to investigate the singularity at the heart of black holes, seeking to resolve the information paradox and determine if these objects represent gateways to other universes. Further studies examine the inflationary epoch immediately following the Big Bang, exploring whether quantum gravity effects could explain the observed homogeneity and isotropy of the cosmos. These explorations aren’t merely academic; they attempt to reconcile observational data from cosmic microwave background radiation with predictions arising from quantum gravity theories, potentially revealing previously unknown physics governing the very early universe and the formation of large-scale structures.

The pursuit of a quantum theory of gravity represents a formidable challenge at the forefront of theoretical physics. Existing frameworks, like general relativity and quantum mechanics, operate successfully within their respective domains, but break down when applied to scenarios where both gravity and quantum effects are significant – such as the singularity within a black hole or the very first moments of the universe. A complete theory must not only reconcile these frameworks mathematically, but also make testable predictions. This is complicated by the incredibly weak nature of gravity at the quantum scale, making direct experimental verification exceedingly difficult. Researchers are exploring various avenues, including searching for subtle quantum gravitational effects in cosmological observations, developing tabletop experiments to detect minuscule gravitational fluctuations, and investigating the potential for gravitational wave astronomy to reveal quantum properties of spacetime, all in the hope of finally bridging the gap between the quantum and the cosmic.

The pursuit of a unified theory hinges on the synergistic potential of several cutting-edge approaches to quantum gravity. Loop Quantum Gravity proposes that spacetime itself is quantized, existing as discrete loops and networks rather than a smooth continuum, while Combinatorial Spacetime explores the possibility that spacetime emerges from fundamental, building-block relationships between points. Crucially, these theoretical frameworks are being refined through ongoing advancements in quantum field theory, which provides the mathematical tools to describe fundamental particles and forces. By integrating the granular spacetime of Loop Quantum Gravity and Combinatorial Spacetime with the established predictive power of quantum field theory, researchers aim to resolve the long-standing incompatibility between general relativity and quantum mechanics – ultimately offering a comprehensive description of all four fundamental forces and the very fabric of reality.

The construction of spacetime from matter fields, as detailed in this work, echoes a fundamental questioning of established frameworks. It’s a precarious dance, building the very stage upon which physics operates from the actors themselves. As Hannah Arendt observed, “The search for the foundations of knowledge is, ironically, a quest for something that does not exist.” This paper, by attempting to derive geometry from matter, risks a similar vanishing point. The renormalization group approach, while offering a path towards consistent quantum gravity, is akin to peering into the abyss – the deeper one goes, the more the established rules seem to warp and laugh at simplified models. The universe, it seems, delights in reminding us of the limits of any constructed theory.

The Horizon Beckons

This construction of spacetime, born from the dynamics of matter itself, is a bold attempt to sidestep the familiar pitfalls of quantizing gravity. The reliance on a combinatorial structure, echoing Penrose’s vision, offers a potentially finite and therefore calculable universe-a seductive notion. Yet, the devil, as always, resides in the details. Demonstrating a genuine connection to the continuous spacetime of general relativity-beyond mathematical correspondence-remains a significant hurdle. The renormalization group analysis, crucial for establishing scale invariance, must navigate the treacherous waters of non-perturbative quantum gravity, where established techniques often falter.

The true test will lie in incorporating a robust description of matter fields within this framework, and in extracting predictions that deviate from, or elegantly explain, existing cosmological observations. The very act of building spacetime from matter implies a radical shift in perspective; it’s a framework that demands a re-evaluation of concepts like locality and causality. This work serves as a reminder that the cosmos generously shows its secrets to those willing to accept that not everything is explainable.

Ultimately, this approach-like all others-may find its event horizon. Black holes are nature’s commentary on human hubris, and any theoretical edifice, no matter how elegantly constructed, is subject to the same fate. The pursuit, however, is valuable not for the answers it may yield, but for the questions it forces one to ask.

Original article: https://arxiv.org/pdf/2602.08341.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/