The Edge of Order: How Quasiperiodicity Shatters Localization

Author: Denis Avetisyan

New research reveals how introducing quasiperiodic order into non-Hermitian systems can dramatically alter electron behavior, leading to either extended states or the emergence of the non-Hermitian skin effect.

The system exhibits tunable, non-reciprocal hopping-characterized by strengths of <span class="katex-eq" data-katex-display="false">J e^{\pm\alpha}</span>-coupled with a quasiperiodic onsite potential <span class="katex-eq" data-katex-display="false">\lambda_{j}</span>, and further refined by an impurity bond whose hopping strength is adjustable via parameter μ. — The system exhibits tunable, non-reciprocal hopping-characterized by strengths of $J e^{\pm\alpha}$ -coupled with a quasiperiodic onsite potential $\lambda_{j}$ , and further refined by an impurity bond whose hopping strength is adjustable via parameter μ.

This study demonstrates a transition from scale-free localization induced by quasiperiodicity, linked to generalized boundary conditions and characterized by entanglement entropy and condition number analysis.

Non-Hermitian systems typically exhibit extreme sensitivity to boundary conditions, yet the interplay between disorder and boundary engineering remains incompletely understood. This research, detailed in ‘Quasiperiodicity-induced non-Hermitian skin effect from the breakdown of scale-free localization’, investigates how quasiperiodic disorder disrupts scale-free localization in a non-reciprocal lattice. Our analyses reveal that quasiperiodicity can induce a transition from localized states to either an extended regime or the non-Hermitian skin effect, dependent on boundary conditions. How do these findings inform our understanding of robust topological phases in actively driven, disordered systems?

Beyond Conventional Boundaries: Embracing the Open System

Conventional condensed matter physics typically employs the mathematical framework of Hermitian Hamiltonians to describe the energy and behavior of materials. However, this approach inherently struggles when addressing systems that aren’t closed – those that exchange energy and matter with their surroundings. Real-world materials are rarely isolated; they often interact with external stimuli, experience dissipation due to internal resistance, or exhibit gain through external driving. The limitations of Hermitian physics in these ‘open’ systems stem from its inability to properly account for these non-conservative processes. Consequently, crucial phenomena like lasing, non-equilibrium behavior, and the response of materials to external fields are often poorly described or entirely missed. This necessitates a departure from strictly Hermitian descriptions to fully capture the rich physics of interacting and dissipating systems.

Non-Hermitian physics represents a significant departure from traditional quantum and condensed matter frameworks by relaxing the requirement that physical observables be represented by Hermitian operators. This extension allows for the explicit inclusion of gain and loss mechanisms within a system’s Hamiltonian, effectively describing scenarios where energy is not conserved – such as systems coupled to an external reservoir or exhibiting internal amplification. The consequences are far-reaching, giving rise to counterintuitive phenomena like exceptional points – singularities in the parameter space where eigenvalues and eigenvectors coalesce – and the existence of unidirectional invisibility. These effects, absent in conventional Hermitian systems, are not merely mathematical curiosities; they manifest in diverse physical platforms, including optical resonators, electronic circuits, and even mechanical metamaterials, opening new avenues for designing devices with unprecedented functionalities and exploring fundamentally new physics.

The conventional framework of condensed matter physics, built upon the principles of Hermitian quantum mechanics, often struggles to accurately model realistic physical systems. Most materials aren’t truly isolated; they constantly interact with their surroundings and are frequently subjected to external forces or energy input. Non-Hermitian physics addresses this limitation by providing the tools to describe open systems – those that exchange energy and matter with their environment. This is not merely a mathematical extension, but a necessary paradigm shift for understanding phenomena ranging from lasers and optical amplifiers-where gain is intentionally introduced-to dissipation in metamaterials and the behavior of biological systems. By explicitly incorporating gain and loss terms into the Hamiltonian, researchers can model how external driving or environmental interactions fundamentally alter a material’s properties, leading to unexpected behaviors like enhanced sensitivity, unidirectional propagation of waves, and the existence of exceptional points where standard physical predictions break down. This broadened theoretical landscape is thus essential for accurately representing-and potentially harnessing-the complex dynamics found in a vast array of physical scenarios.

The Emergence of Localized States: A New Form of Boundary Sensitivity

The Non-Hermitian Skin Effect (NHSE) is characterized by the exponential decay of the probability amplitude of an eigenstate as one moves into the bulk of the system from its boundary. This means that, unlike typical localized states arising from disorder, the NHSE results in all eigenstates being concentrated at one or both boundaries of the system, even in the absence of any disorder. Mathematically, this localization is evidenced by a localization length ξ which becomes system-size dependent, contrasting with the finite and system-independent localization lengths observed in disordered Hermitian systems. The effect is a direct consequence of the broken parity-Hermitian symmetry inherent in non-Hermitian systems, leading to a non-trivial topology in the Brillouin zone and ultimately, this boundary-localized behavior.

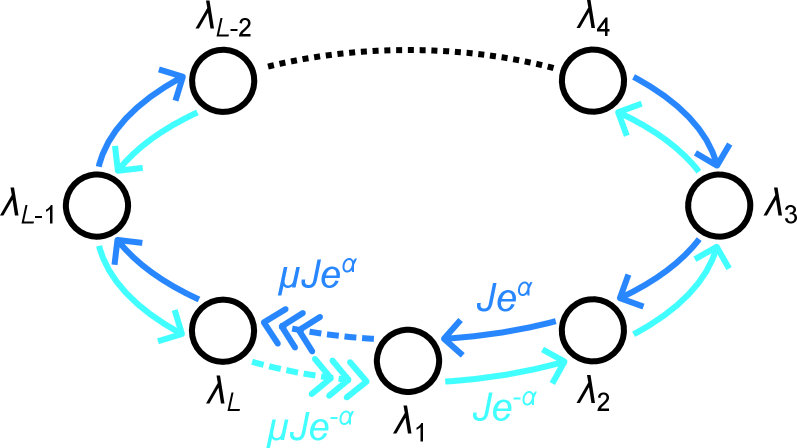
Non-reciprocal hopping, the foundational mechanism behind the Non-Hermitian Skin Effect, describes a system where the transition probability between lattice sites $i$ and $j$ is not necessarily equal to the probability of transitioning from $j$ to $i$ . Mathematically, this is expressed as $t_{ij} \neq t_{ji}$ , where $t_{ij}$ represents the hopping amplitude. This asymmetry introduces a directional bias in the system’s dynamics; a particle is more likely to move in one direction than the other. Consequently, wavefunctions are no longer evenly distributed throughout the lattice, but instead accumulate at specific boundaries due to this preferential hopping, leading to the observed exponential localization. The degree of asymmetry in the hopping amplitudes directly correlates with the strength of the localization effect.

The Hatano-Nelson model, a one-dimensional tight-binding model, serves as a foundational example of the Non-Hermitian Skin Effect. It is defined by hopping terms $t_{ij}$ where $t_{i,i+1} = 1$ and $t_{i+1,i} = \gamma$ , with γ representing a real-valued parameter. This asymmetry in hopping, or non-reciprocity, fundamentally distinguishes it from traditional Hermitian systems. Solutions to the eigenvalue problem demonstrate that all eigenstates are localized at one of the boundaries of the system, with the localization length inversely proportional to $|\ln(\gamma)|$ . The parameter γ controls the degree of non-reciprocity and consequently, the strength of the boundary localization; as γ deviates from unity, the eigenstates increasingly concentrate at the system’s edges.

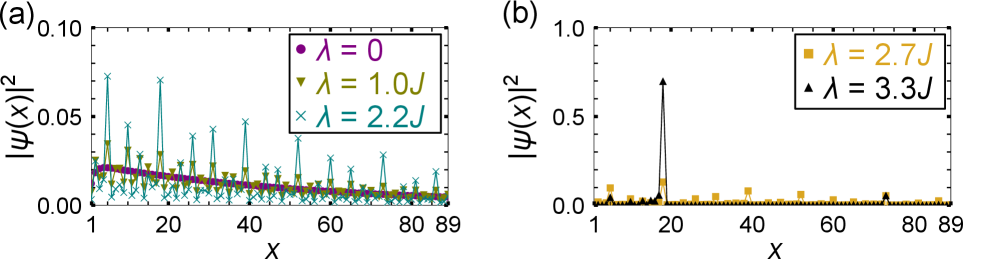
The localization length, a key parameter describing the spatial extent of a wave function, undergoes a significant alteration in systems exhibiting the Non-Hermitian Skin Effect. Specifically, as observed in the $\hat{H}$ model with L=89, the system transitions from a regime of scale-free localization, where the localization length varies proportionally with system size, to a regime characterized by exponential localization. This change indicates a fundamental shift in the wave function’s behavior; instead of spreading diffusely, the wave function becomes increasingly confined to the boundaries of the system, with a localization length that is drastically reduced and independent of system size beyond a certain point. This alteration is a direct consequence of the non-reciprocal hopping terms, which introduce asymmetry into the system and drive the boundary accumulation of eigenstates.

The spatial density distribution <span class="katex-eq" data-katex-display="false">|\psi(x)|^{2}</span> reveals distinct behaviors for <span class="katex-eq" data-katex-display="false">L=89</span>, <span class="katex-eq" data-katex-display="false">\ln\mu=-0.5</span>, and <span class="katex-eq" data-katex-display="false">\phi=0</span>, exhibiting either spread-out states (a) or localized states (b). — The spatial density distribution $|\psi(x)|^{2}$ reveals distinct behaviors for $L=89$ , $\ln\mu=-0.5$ , and $\phi=0$ , exhibiting either spread-out states (a) or localized states (b).

Diagnosing Sensitivity: Unveiling Localization Through System Properties

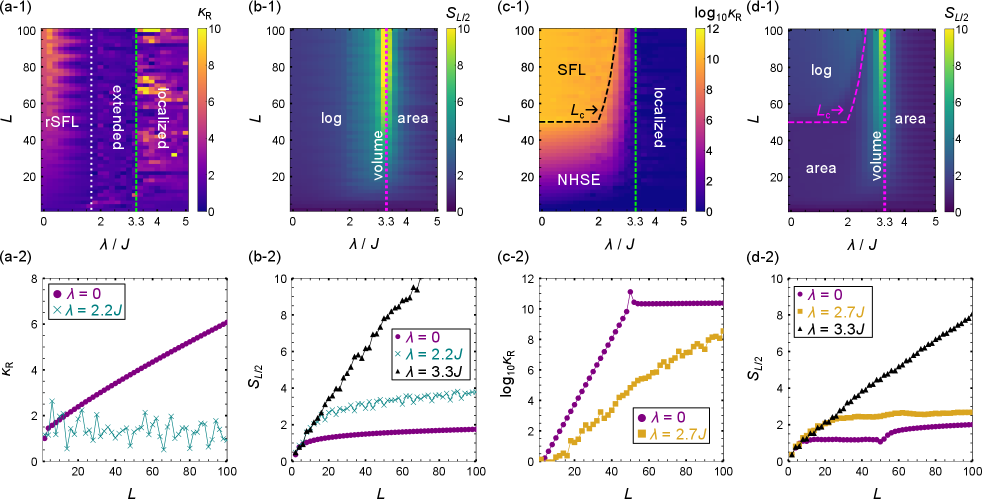
The Condition Number, calculated as the ratio of the largest to the smallest singular value of the Hamiltonian κ, serves as a quantitative indicator of non-normality and, consequently, the Non-Hermitian Skin Effect. A Condition Number of 1 indicates a normal, Hermitian system. Values significantly greater than 1 denote non-normality, with larger values correlating to a stronger Skin Effect and increased sensitivity to boundary conditions. This metric directly reflects the degree to which the left and right eigenvectors of the Hamiltonian are misaligned, a defining characteristic of non-Hermitian systems exhibiting the Skin Effect; therefore, it provides a readily computable measure of the effect’s magnitude without requiring direct calculation of the system’s wave functions.

The Non-Normality Ratio serves as a diagnostic tool for identifying localization regimes within non-Hermitian systems by quantifying sensitivity to infinitesimal perturbations. This ratio is directly related to the system’s localization length ξ; stronger localization – a smaller ξ – results in a higher Non-Normality Ratio, indicating greater susceptibility to change from external influences. Conversely, extended states, characterized by a larger ξ, exhibit a lower ratio, signifying robustness against perturbations. This scaling behavior allows for efficient differentiation between localization regimes without requiring detailed calculations of the wave function, providing a computationally advantageous alternative to traditional localization analysis.

Traditional analysis of the Non-Hermitian Skin Effect often requires detailed calculation of the system’s wave functions, a process which can be computationally expensive, particularly for large or complex systems. Condition numbers and the Non-Normality Ratio provide alternative diagnostic tools that circumvent this need. By quantifying the sensitivity of the system to perturbations – as indicated by the condition number – and analyzing scaling behavior related to the localization length ξ via the Non-Normality Ratio, researchers can robustly assess the presence and strength of the Skin Effect without explicitly solving for the wave function. This offers a significant advantage in scenarios where computational resources are limited or a rapid assessment is required, allowing for efficient characterization of non-Hermitian systems.

Traditional analysis of localization in non-Hermitian systems often involves direct calculation of wave functions and their spatial decay, a process that scales poorly with system size and dimensionality. For systems exhibiting many degrees of freedom, or complex geometries, these calculations become computationally prohibitive, requiring significant resources and time. The use of condition numbers and non-normality ratios offers a valuable alternative, providing a quantitative assessment of the Non-Hermitian Skin Effect without explicitly solving for the wave function. This approach reduces computational complexity, enabling the characterization of localization behavior in systems where direct wave function analysis is impractical or impossible, particularly in areas such as disordered systems, topological photonics, and acoustic metamaterials.

Regime diagrams based on non-normality ratios and energy efficiency (EE) reveal scaling behavior of <span class="katex-eq" data-katex-display="false">\kappa_R</span> and <span class="katex-eq" data-katex-display="false">EE_{L/2}</span> across different values of <span class="katex-eq" data-katex-display="false">\ln\mu</span>, with a critical length <span class="katex-eq" data-katex-display="false">L_c</span> identified consistent with previous findings. — Regime diagrams based on non-normality ratios and energy efficiency (EE) reveal scaling behavior of $\kappa_R$ and $EE_{L/2}$ across different values of $\ln\mu$ , with a critical length $L_c$ identified consistent with previous findings.

Engineering Confinement: Tailoring Boundary Conditions for Precise Control

Conventional simulations often rely on either open boundary conditions, which mimic finite-size systems and introduce edge effects, or periodic boundary conditions, which effectively create an infinite system but can artificially suppress localization. Generalized boundary conditions offer a powerful alternative by allowing a continuous transition between these extremes. This is achieved through the introduction of a tunable parameter that controls the coupling between the edges of the system; a value of zero corresponds to open boundaries, while an infinite value replicates the periodicity. Consequently, researchers can systematically explore how boundary effects influence system behavior, engineering conditions that promote or suppress localization phenomena and providing a more nuanced understanding of wave propagation and quantum transport in diverse physical systems. This level of control is crucial for accurately modeling real-world materials and devices where boundary conditions are rarely strictly one or the other.

Recent advancements demonstrate the ability to engineer systems exhibiting a unique form of localization known as scale-free localization. Unlike conventional localized states where the extent of localization remains fixed, or diminishes with system size, scale-free localization features localization lengths that scale linearly with the overall system size. This means that as the system expands, the region over which a particle or excitation remains confined expands proportionally, maintaining a consistent degree of confinement relative to the system’s dimensions. This behavior arises from carefully tuning boundary conditions and system parameters, enabling the creation of systems where localization isn’t a fixed property, but a scalable characteristic-potentially unlocking new avenues for controlling and manipulating wave phenomena in diverse physical settings. The predictable relationship between system size and localization length $\xi \propto L$ offers unprecedented control over wave propagation and opens possibilities for designing materials with tailored transport properties.

Investigations into the relationship between boundary conditions and system parameters have uncovered a surprisingly complex phase diagram governing the behavior of localized states. By systematically varying these factors, researchers demonstrate the ability to finely tune the degree of localization within a system; transitioning from fully extended states to strongly localized ones, and exploring intermediate regimes. This control isn’t merely qualitative; subtle adjustments to boundary conditions can induce transitions between fully localized states, extended states, and more exotic phases exhibiting critical behavior. Consequently, materials exhibiting controlled localization can be envisioned for applications demanding precise wave confinement, such as high-sensitivity sensors, efficient energy harvesting devices, and robust quantum information storage systems. The ability to sculpt the localization landscape opens exciting possibilities for creating materials where wave behavior is not simply a consequence of inherent properties, but a carefully programmed response to external stimuli.

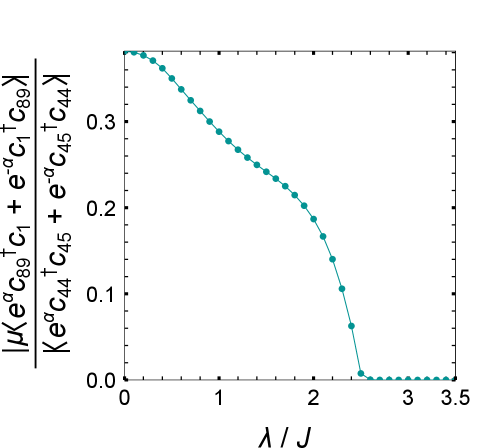
Investigations are increasingly directed towards leveraging the interplay between quasiperiodicity and non-Hermitian physics for practical technologies, particularly in the realms of wave control, advanced sensing, and quantum information science. Current research highlights a pivotal transition point around a quasiperiodic potential strength of 2.6J, where system behavior undergoes a significant shift. Prior to the formation of extended states within the material’s bulk, a suppression of electron hopping between the system’s edges emerges – a phenomenon crucial for maintaining localized states and preventing signal degradation. This precise control over localization, achieved through manipulation of system parameters, promises the development of robust and efficient devices capable of manipulating waves and encoding quantum information with unprecedented precision, and lays the groundwork for materials designed with tailored electromagnetic or quantum properties.

The ratio of boundary to bulk hopping expectations decreases with increasing quasiperiodic potential strength λ, exhibiting a critical value of approximately <span class="katex-eq" data-katex-display="false">3.3J</span> as observed with parameters consistent with Figure 3. — The ratio of boundary to bulk hopping expectations decreases with increasing quasiperiodic potential strength λ, exhibiting a critical value of approximately $3.3J$ as observed with parameters consistent with Figure 3.

A New Frontier: Quasiperiodicity and Non-Hermiticity – Unveiling Novel Physics

The intersection of quasiperiodic order and non-Hermitian physics is revealing unexpectedly rich landscapes of wave localization. Traditional studies of localization, such as those concerning disordered systems, have been significantly broadened by considering systems possessing long-range order – specifically, quasiperiodicity – alongside non-Hermitian elements that break the symmetry of energy spectra. This combination doesn’t simply modify existing localization phenomena; it generates entirely new scenarios where localization can be dynamically tuned, enhanced, or even reversed by manipulating non-Hermitian parameters. The resulting wave functions exhibit complex spatial distributions, often drastically different from those found in either purely quasiperiodic or purely disordered systems. Consequently, this synergistic effect is establishing a new frontier for understanding and controlling wave behavior in a wide range of physical platforms, from photonic crystals to topological materials.

The interplay between quasiperiodicity and non-Hermitian physics dramatically alters the behavior of systems like the Aubry-Andre-Harper (AAH) model, leading to unconventional localization transitions. Traditionally, the AAH model-a cornerstone of condensed matter physics-exhibits a clear metal-insulator transition as a function of potential strength. However, introducing non-Hermitian terms – which violate the requirement that a system’s energy remains real – fundamentally reshapes this behavior. Researchers have discovered that these non-Hermitian perturbations can induce novel localization phases, including scenarios where localization occurs even in the absence of a conventional band gap. Furthermore, the nature of the localization transition itself can change, becoming smoother or even exhibiting multiple critical points. These transitions are characterized by alterations in the system’s spectral properties and the emergence of topologically protected edge states, offering a pathway to manipulate and control the flow of waves within the material.

The manipulation of localization phenomena through precise control of boundary conditions and system parameters presents a pathway towards the rational design of materials with specifically tailored properties. By engineering the environment in which waves – whether they be electronic, photonic, or acoustic – propagate, researchers can dictate the degree to which these waves are confined or allowed to spread. This control isn’t merely qualitative; subtle adjustments to boundary conditions can induce transitions between fully localized states, extended states, and more exotic phases exhibiting critical behavior. Consequently, materials exhibiting controlled localization can be envisioned for applications demanding precise wave confinement, such as high-sensitivity sensors, efficient energy harvesting devices, and robust quantum information storage systems. The ability to sculpt the localization landscape opens exciting possibilities for creating materials where wave behavior is not simply a consequence of inherent properties, but a carefully programmed response to external stimuli.

The study of quasiperiodic systems reveals a delicate balance between order and disorder, mirroring a fundamental principle applicable to design itself. The transition from scale-free localization to the non-Hermitian skin effect, contingent on system parameters and boundary conditions, highlights how seemingly minor adjustments can dramatically alter a system’s overall behavior. This resonates with the notion that elegance arises not from complexity, but from a refined understanding of underlying principles. As Immanuel Kant observed, “Out of sheer inclination, no one would ever impose restrictions on himself; but if he does so, it is always for the sake of a higher purpose.” The imposition of quasiperiodicity, akin to Kant’s self-imposed restrictions, unveils previously hidden properties, demonstrating that constraint, when thoughtfully applied, can unlock deeper aesthetic and functional harmony.

The Horizon Beckons

The demonstration that quasiperiodicity can sculpt the fate of non-Hermitian systems – steering them from scale-free localization toward either extension or the notorious skin effect – feels less like an answer and more like a carefully tuned question. The interplay revealed between boundary conditions and system parameters is, predictably, not a simple one. Ideal design unites form and function; here, it seems, both are intimately linked to the very way a system interrogates its edges. The condition number, a metric of sensitivity, becomes more than a diagnostic; it’s a whisper of the underlying instability, a hint that robust design is a matter of careful balancing, not brute force.

Future work will undoubtedly probe the limits of this control. Is there a universal principle governing these transitions, a form of ‘localization landscape’ where the fate of any non-Hermitian quasiperiodic system can be predicted? Or is the field destined to catalog exceptions, forever chasing a harmonious geometry that remains just beyond reach? The entanglement entropy, though informative, feels incomplete; a full characterization of the underlying many-body physics demands a more holistic view-one that acknowledges the system’s sensitivity to even the smallest perturbation.

Ultimately, this research highlights a fundamental truth: elegance isn’t optional. Every system element should occupy its place, creating cohesion. Systems that shout-those burdened by unnecessary complexity or ill-defined boundaries-will always lack the subtle power of those that whisper.

Original article: https://arxiv.org/pdf/2602.11155.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/