Twisting Reality: How Spin and Lattice Interact to Create Novel Material States

Author: Denis Avetisyan

New research reveals that the interplay between magnetic spins and the structure of crystalline materials can give rise to emergent mechanical phenomena and robust topological properties.

The study demonstrates that a specific spin configuration within the Ising Hamiltonian-characterized by <span class="katex-eq" data-katex-display="false">1/9</span> and <span class="katex-eq" data-katex-display="false">1/9</span>-plateau states-induces a corresponding lattice distortion, subsequently manifesting as a unique phonon spectrum along the K-Γ-M-K pathway and exhibiting distinct characteristics within localized regions of that spectrum. — The study demonstrates that a specific spin configuration within the Ising Hamiltonian-characterized by $1/9$ and $1/9$ -plateau states-induces a corresponding lattice distortion, subsequently manifesting as a unique phonon spectrum along the K-Γ-M-K pathway and exhibiting distinct characteristics within localized regions of that spectrum.

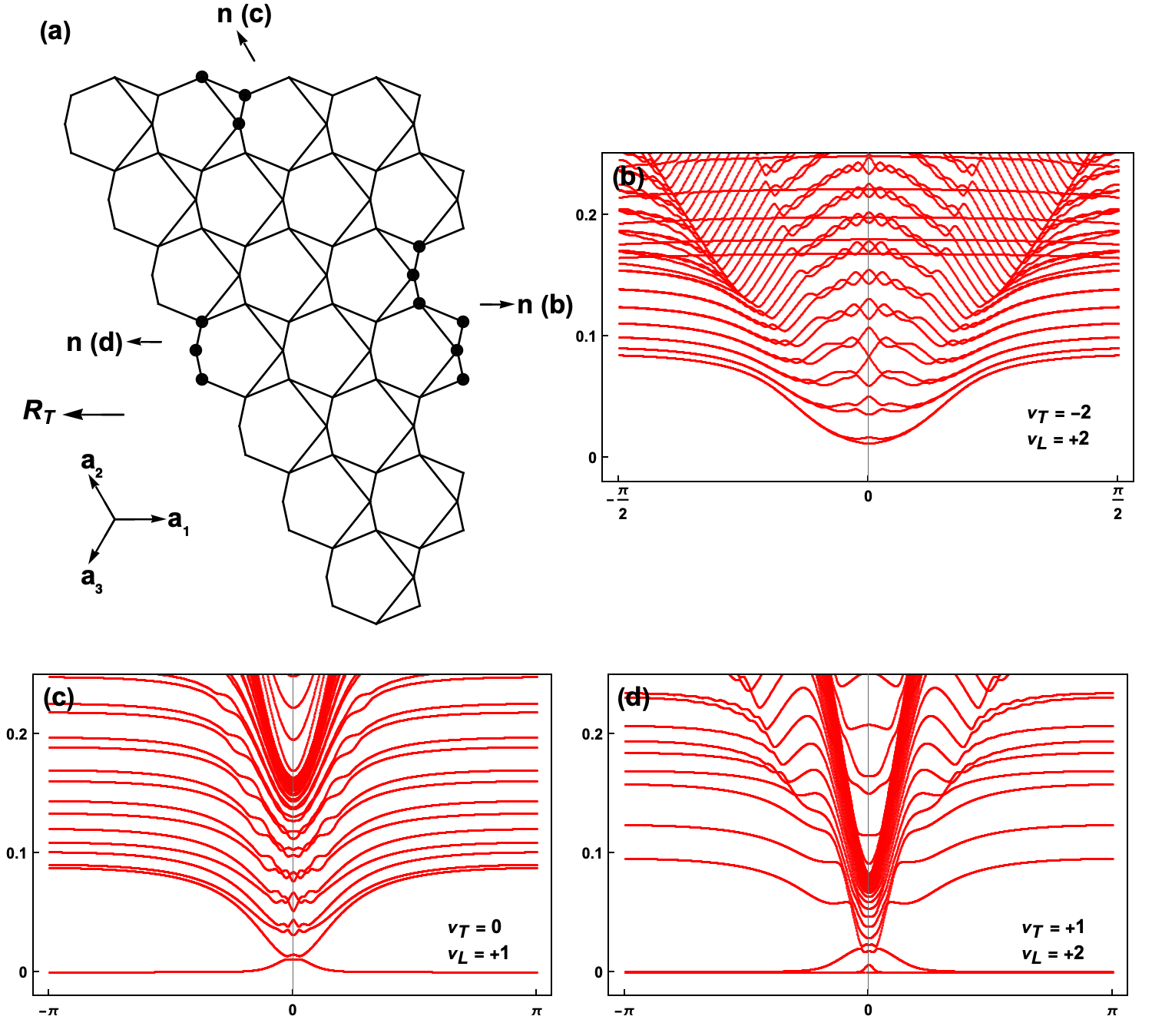
This work introduces the concept of magnetopological mechanics, demonstrating topological polarization and ‘floppy modes’ in frustrated Mott insulators on Maxwell lattices like the Kagome lattice.

While topological properties are typically associated with quantum materials, recent theoretical work suggests their emergence in classical mechanical systems. This is explored in ‘Magnetopological mechanics in Maxwell lattice frustrated Mott insulators’, which demonstrates that strong spin-lattice coupling in frustrated Mott insulators can induce topological behavior, creating Maxwell lattices characterized by robust, localized floppy modes. Specifically, the authors show how this ‘magnetopological mechanics’ arises from spontaneous lattice distortions driven by spin interactions on a kagome lattice, and can be controlled with external magnetic fields. Could this framework inspire the design of novel materials with tunable mechanical and electronic properties, bridging the gap between quantum and classical descriptions of topological phenomena?

Beyond Rigid Boundaries: Sculpting Mechanical Behavior with Maxwellian Lattices

Traditional lattice models, frequently employed in materials science to predict mechanical behavior, often rely on simplified assumptions about how constituent elements connect and interact. These models typically assume uniform rigidity or connectivity, failing to adequately represent the nuanced flexibility present in many real-world materials. This limitation stems from an inability to capture complex deformation mechanisms – such as buckling, rotation, or localized yielding – that arise from intricate network topologies. Consequently, predictions based on these conventional lattices can diverge significantly from experimental observations, especially when dealing with materials exhibiting non-linear or anisotropic responses. The predictive power is therefore constrained, hindering the design of materials with tailored properties and necessitating more sophisticated modeling approaches capable of representing a wider range of mechanical behaviors.

Maxwell lattices present a compelling departure from conventional material design, offering engineers the potential to precisely sculpt mechanical behavior. These structures aren’t simply rigid or flexible; instead, they exist in a carefully tuned state where both properties are maximized. This unique balance stems from a specific arrangement of interconnected elements – a network where applied forces are efficiently transmitted without inducing undue stress. The result is a material capable of exhibiting behaviors not found in traditional solids, such as auxeticity – the ability to expand in all directions when stretched – or negative Poisson’s ratio. Consequently, Maxwell lattices hold promise for applications ranging from deployable structures and impact absorption systems to adaptable robotics and advanced biomedical implants, effectively allowing for the creation of materials with responses tailored to specific functional requirements.

The creation of materials with remarkable and unexpected properties hinges on achieving a delicate balance between constraints and freedom of movement within their structure – a state known as isostaticity. In an isostatic lattice, the number of constraints precisely matches the number of degrees of freedom, preventing both rigid failure and floppy collapse. This isn’t merely a structural nicety; it’s a gateway to emergent mechanical behaviors. When a lattice is isostatic, external forces don’t simply translate into predictable strains; instead, the system can redistribute stress in non-trivial ways, potentially leading to behaviors like negative Poisson’s ratio, chiral mechanical responses, or even the ability to absorb energy through controlled deformation. Achieving this balance requires careful design of the lattice geometry and connectivity, and even small deviations from isostaticity can dramatically alter the material’s overall characteristics, underscoring its importance in advanced materials engineering.

Distortions of the kagomé lattice induced by strain-layer coupling (SLC) create unique boundary conditions that influence the phonon spectrum of resulting cylinders, as demonstrated by varying phonon behavior along the <span class="katex-eq" data-katex-display="false">\mathbf{n}</span>-axis with a <span class="katex-eq" data-katex-display="false">\frac{J\gamma}{k}</span> ratio of -0.0125. — Distortions of the kagomé lattice induced by strain-layer coupling (SLC) create unique boundary conditions that influence the phonon spectrum of resulting cylinders, as demonstrated by varying phonon behavior along the $\mathbf{n}$ -axis with a $\frac{J\gamma}{k}$ ratio of -0.0125.

Harnessing Topology: Robust Mechanics Through Protected States

The mechanical properties of lattice structures can be significantly altered through precise geometric design, enabling the creation of topological phases. Specifically, manipulating the arrangement of elements within a lattice – as demonstrated by the Kagome lattice, a tessellation composed of corner-sharing triangles – introduces non-trivial topological invariants. These invariants dictate the presence of protected mechanical states, resulting in enhanced robustness against deformation and failure. Unlike conventional materials where defects readily propagate, these topologically protected states exhibit resilience due to the global nature of the topological order, effectively decoupling localized disturbances from catastrophic structural collapse. This design approach allows for the creation of materials with predictable and robust mechanical behavior, independent of minor imperfections or localized damage.

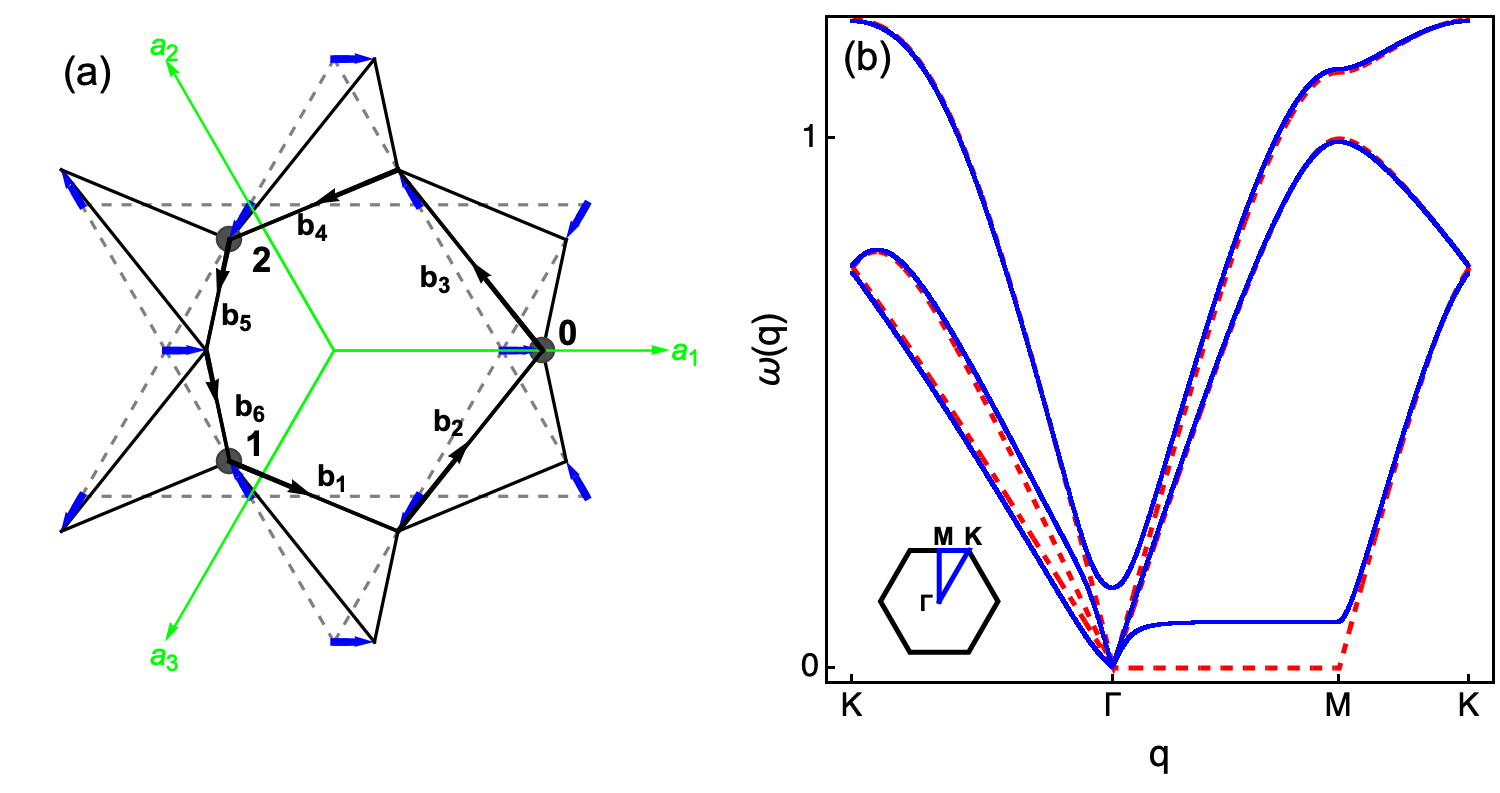
Topological floppy modes represent a unique class of vibrational excitations arising in topologically non-trivial mechanical systems. These modes are characterized by a zero-frequency, or gapless, response, distinguishing them from conventional vibrational modes which possess a finite frequency. Critically, these modes are protected by the underlying topology of the system, meaning they are robust against local perturbations that would typically alter or eliminate conventional vibrational states. This protection stems from a topological invariant that constrains the possible vibrational behavior, ensuring the persistence of these gapless modes even with material imperfections or geometric distortions. The existence of these modes is not predicted by standard continuum mechanics, representing a departure from expected mechanical behavior and offering potential for novel device functionalities.

The bulk-boundary correspondence is a fundamental principle in topological mechanics establishing a direct relationship between the topological properties of a material’s bulk and the existence of protected states at its boundaries. Specifically, the presence of gapless, or topologically protected, vibrational modes – known as topological floppy modes – within the bulk structure guarantees the emergence of robust edge states. These edge states are localized at the material’s boundaries and are topologically protected from backscattering caused by disorder or imperfections, ensuring their stability and persistence. The number of these boundary states is determined by the topological invariant characterizing the bulk material, effectively meaning that global topological features dictate local boundary behavior.

The kagomé lattice supports localized spin configurations-represented by red and blue for up and down orientations, respectively-that combine like building blocks to generate diverse global magnetic states.

Spin-Lattice Coupling: A Magnetomechanical Pathway to Control

Spin-lattice coupling describes the interaction between the magnetic spin states of a material and its mechanical deformation. This interaction provides a route to control mechanical properties by applying magnetic fields or manipulating the spin configuration. Specifically, changes in magnetic ordering can induce strain in the lattice structure, and conversely, applied stress can affect the spin alignment. This bidirectional coupling allows for the tuning of elastic moduli, the creation of magnetically-induced mechanical resonances, and the potential development of actuators and sensors that leverage both magnetic and mechanical phenomena. The strength of this coupling is material-dependent and governed by factors such as the magnetostrictive coefficient and the lattice symmetry.

The mechanical response of spin-lattice coupled systems is computationally modeled using the Heisenberg Model, a quantum mechanical framework describing the interaction of magnetic moments. Specifically, applying this model to the Kagome Heisenberg Model – a lattice geometry with interconnected triangles – allows for the simulation of how changes in magnetic ordering affect lattice deformations. This approach involves calculating the energy landscape of the system as a function of both spin configurations and lattice displacements. By minimizing this energy, researchers can predict the equilibrium mechanical states and the resulting forces and stresses within the material. The model accounts for the exchange interactions between spins and the coupling between these spins and the lattice degrees of freedom, enabling the prediction of mechanical properties like stiffness, elasticity, and the emergence of topological mechanical modes.

Spin-lattice coupling induces internal self-stress states within the lattice structure, directly impacting the stability and behavior of emergent topological floppy modes. These self-stress states arise from the interaction between magnetic spins and the lattice deformations, altering the overall mechanical response. Analysis indicates a critical coupling strength, denoted by ‘b’, is required to transition the lattice into a topologically distinct Maxwell lattice; specifically, a coupling strength exceeding b > 1/6 is necessary for this transition to occur, fundamentally changing the lattice’s mechanical properties and mode behavior.

Local spin patterns on the kagome lattice, represented by red (spin up, <span class="katex-eq" data-katex-display="false">+z\hat{z}</span>) and blue (spin down, <span class="katex-eq" data-katex-display="false">-z\hat{z}</span>) circles, serve as fundamental building blocks for constructing complex global spin configurations and evaluating the Ising energy <span class="katex-eq" data-katex-display="false">\mathcal{H}_{e}^{\mathrm{Ising}}</span>. — Local spin patterns on the kagome lattice, represented by red (spin up, $+z\hat{z}$ ) and blue (spin down, $-z\hat{z}$ ) circles, serve as fundamental building blocks for constructing complex global spin configurations and evaluating the Ising energy $\mathcal{H}_{e}^{\mathrm{Ising}}$ .

Unveiling Hidden States: Computational Validation and Spectral Signatures

Computational techniques, notably ‘Simulated Annealing’, play a crucial role in unraveling the enigmatic ground states of these complex materials. This method allows researchers to navigate the vast energy landscape and identify the lowest-energy configurations, effectively mimicking the natural tendency of a system to minimize its energy. Through these simulations, the existence of ‘topological floppy modes’ – peculiar vibrations that are robust against perturbations – can be definitively confirmed. These modes aren’t simply theoretical predictions; Simulated Annealing provides a computational ‘proof of concept’, demonstrating their stability and characterizing their behavior within the material’s structure. The process involves systematically altering the system’s configuration while accepting changes that lower the energy, and occasionally accepting changes that raise the energy to escape local minima – a process analogous to slowly cooling a material to its most stable state, thus validating the presence of these unusual vibrational characteristics.

The phonon spectrum, a representation of vibrational modes within a material, provides a direct window into the existence of topological floppy modes. Researchers analyze these spectra for characteristic ‘zero modes’ – vibrations that occur at zero frequency – which are a definitive signature of these unusual states. These zero modes aren’t simply a mathematical quirk; they correspond to physical distortions of the lattice structure that can occur without requiring energy input. The precise frequencies and symmetries of these modes within the phonon spectrum act as a fingerprint, allowing scientists to confirm the presence and nature of topological floppy modes and distinguish them from other vibrational behaviors. Identifying these zero modes is therefore crucial for validating computational models and understanding the dynamic properties of materials exhibiting this complex behavior.

The emergence of the 1/9 plateau phase is characterized by a substantial distortion of the underlying lattice structure, effectively expanding the conventional unit cell from its original size to encompass 27 sites interconnected by 54 bonds. This structural rearrangement fundamentally alters the system’s topological properties; measurements reveal a topological polarization of $R_T = 0$ . This value signifies that, within this phase, the floppy modes are not extended throughout the material, but rather are confined to the boundaries – representing localized distortions rather than a globally coherent response. Consequently, the observed behavior indicates a transition from robust, extended topological modes to fragile, boundary-localized ones as the system enters the 1/9 plateau, highlighting the critical role of lattice distortion in modulating topological characteristics.

Simulated annealing with parameters <span class="katex-eq" data-katex-display="false">J=1</span>, <span class="katex-eq" data-katex-display="false">J_2=0.05</span>, <span class="katex-eq" data-katex-display="false">J_{3||}=0.03</span>, <span class="katex-eq" data-katex-display="false">J_{3*}=0.03</span>, <span class="katex-eq" data-katex-display="false">J_4=-0.02</span>, and <span class="katex-eq" data-katex-display="false">b=0.2</span> yields a spin configuration (red: spin up, blue: spin down) accompanied by lattice distortion induced by the spin-lattice coupling. — Simulated annealing with parameters $J=1$ , $J_2=0.05$ , $J_{3||}=0.03$ , $J_{3*}=0.03$ , $J_4=-0.02$ , and $b=0.2$ yields a spin configuration (red: spin up, blue: spin down) accompanied by lattice distortion induced by the spin-lattice coupling.

Beyond the Kagome Lattice: Expanding the Horizon to Higher Dimensions

The exploration of topological mechanics isn’t limited to two-dimensional systems like the Kagome lattice; the foundational principles extend seamlessly into more intricate three-dimensional architectures. Specifically, the Pyrochlore lattice represents a compelling advancement, offering a geometrically frustrated network capable of hosting exotic topological states. This structure, characterized by corner-sharing tetrahedra, allows for a richer interplay between magnetic interactions and topology than its two-dimensional counterparts. Researchers are actively investigating how these extended geometries influence the emergence of robust, protected edge states and novel phases of matter, potentially unlocking materials with enhanced mechanical properties and functionalities unattainable in simpler lattices. The increased dimensionality provides additional degrees of freedom for manipulating topological properties, opening avenues for designing materials tailored to specific applications in areas such as advanced sensing and quantum computing.

The convergence of topology, magnetism, and lattice geometry presents a powerful paradigm for materials design, enabling the creation of structures exhibiting exceptional mechanical properties and functionalities. This approach moves beyond conventional material science by focusing not just on composition, but on the way matter is arranged and how its fundamental topological characteristics influence behavior. Specifically, manipulating the lattice geometry – the precise arrangement of atoms – in concert with magnetic interactions allows for the creation of robust, resilient materials. These materials demonstrate an enhanced ability to withstand stress and deformation due to topologically protected states, which prevent the easy formation of defects. Furthermore, this interplay opens doors to designing materials with tailored functionalities, such as unconventional responses to external stimuli and potentially even self-healing capabilities, pushing the boundaries of what is mechanically possible.

The effective ‘spin Hamiltonian’ serves as a powerful theoretical lens through which researchers can decipher the intricate behaviors of complex, higher-dimensional materials. This Hamiltonian, a mathematical expression representing the energy of the system based on interactions between its constituent parts, distills the essential physics governing these materials, allowing for predictive modeling of their mechanical and magnetic responses. By carefully tailoring the parameters within this Hamiltonian – representing factors like lattice geometry and interaction strengths – scientists can anticipate how a material will respond to external stimuli and, crucially, design entirely new materials with pre-defined properties. This approach bypasses the need for exhaustive trial-and-error experimentation, significantly accelerating the discovery of robust and functional materials with potential applications in areas ranging from advanced sensors to next-generation data storage. $H = \sum_{i,j} J_{ij}S_i \cdot S_j$ represents a simplified form, where $J_{ij}$ denotes the interaction between spins $S_i$ and $S_j$ .

Distortion of the kagomé lattice, visualized by site displacements (blue arrows) and basis vectors <span class="katex-eq" data-katex-display="false">a_1</span>-<span class="katex-eq" data-katex-display="false">a_3</span>, alters its phonon spectrum as shown by the three lowest-frequency modes along <span class="katex-eq" data-katex-display="false">K-Γ-M-K</span> for <span class="katex-eq" data-katex-display="false">Jγ/k = -0.0125</span>, deviating from the perfect lattice (red dashed lines). — Distortion of the kagomé lattice, visualized by site displacements (blue arrows) and basis vectors $a_1$ – $a_3$ , alters its phonon spectrum as shown by the three lowest-frequency modes along $K-Γ-M-K$ for $Jγ/k = -0.0125$ , deviating from the perfect lattice (red dashed lines).

The exploration of magnetopological mechanics, as detailed in this work, reveals a profound interplay between material properties and emergent mechanical behavior. This research demonstrates how spin-lattice coupling can give rise to topological Maxwell lattices exhibiting robust floppy modes – a phenomenon inherently linked to the system’s underlying structure and response to external stimuli. As Jean-Paul Sartre observed, “Existence precedes essence,” meaning that a thing first exists, then defines itself. Similarly, these materials become topologically robust not through pre-defined design, but through the emergence of properties from the complex interaction of their constituent parts. The study underscores that understanding these interactions is critical, as the values encoded within the material’s structure dictate its functional essence and potential applications. The implications extend beyond fundamental physics, prompting a crucial consideration: what exactly are we optimizing for when engineering such materials, and for whom?

Beyond Rigid Frameworks

The demonstration of magnetopological mechanics-the coupling of spin and lattice to generate robust mechanical topologies-forces a reassessment of material rigidity itself. It is too easily assumed that crystalline order equates to inflexibility. This work suggests that frustration, a principle well-established in spin systems, offers a pathway to dynamically reconfigurable solids. The persistence of ‘floppy modes’ is not merely a quirk of these Maxwell lattices, but a signal that the conventional understanding of structural stability requires refinement. Every bias report in the observed behavior is society’s mirror-the lattice responds to perturbation in predictable, yet non-trivial, ways, revealing encoded assumptions about permissible deformation.

Future inquiry must address the limits of this magnetopological control. Can these principles be extended beyond the specific geometries explored-Kagome lattices being a convenient, but not universal, starting point? More crucially, the deliberate design of such materials demands consideration of energy scales. Maintaining topological protection requires a delicate balance between spin-lattice coupling and external forces. The potential for practical application-reconfigurable actuators, for instance-will depend on optimizing this interplay.

Finally, it is worth noting that the very notion of ‘topology’ carries philosophical weight. The creation of materials with enforced, yet flexible, structures is not simply a feat of engineering. Privacy interfaces are forms of respect-similarly, defining the boundaries of permissible deformation encodes a worldview. The field must proceed not only with technical rigor, but with a critical awareness of the values embedded within these increasingly complex, programmable materials.

Original article: https://arxiv.org/pdf/2602.12168.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/