Author: Denis Avetisyan
New research highlights the importance of accurately modeling dark matter distributions around merging black holes to unlock the full potential of future gravitational wave observations.
Relativistic effects and radial pressure within dark matter halos significantly influence the waveforms of extreme mass ratio inspirals, demanding refined theoretical models.
Despite the growing evidence for dark matter, accurately modeling its distribution around compact objects remains a significant challenge. This research, titled ‘Dark matter distributions around extreme mass ratio inspirals: effects of radial pressure and relativistic treatment’, investigates how different treatments of dark matter density profiles impact the orbital evolution and gravitational wave signatures of extreme mass ratio inspirals. We demonstrate that incorporating radial pressure and a fully relativistic treatment substantially alters both the dynamics and detectability of these systems, leading to potentially significant differences in observed waveforms. Could these subtle effects provide a novel pathway for probing the nature of dark matter with future gravitational wave observatories?
The Subtle Dance of Spacetime and Dark Matter
The spacetime surrounding a massive black hole isn’t empty; it’s often enveloped by a halo of dark matter, and this distribution fundamentally warps the gravitational landscape. As a smaller, stellar-mass compact object spirals inward towards the supermassive black hole, it doesn’t follow a simple, Keplerian orbit. Instead, the dark matter halo introduces perturbations, altering the inspiral’s frequency and phase. These effects are subtle, yet critical, because they shift the emitted gravitational wave signal. The precise nature of these alterations depends on the density and extent of the dark matter halo, meaning that analyzing these waveforms offers a potential avenue for probing the distribution of dark matter itself. The influence is particularly pronounced at the later stages of the inspiral, where the compact object is closest to the event horizon, and accurate modeling – including fully relativistic treatments – is essential to extract meaningful information from the gravitational wave signal, especially for systems with compactness levels as low as M/a_0 \approx 10^{-5}.
Current modeling of Extreme Mass Ratio Inspirals (EMRIs), where a stellar-mass object spirals into a supermassive black hole, frequently simplifies the surrounding environment, overlooking the influence of dark matter halos. These halos, though seemingly distant, subtly warp spacetime around the larger black hole, creating deviations from the waveforms predicted by standard calculations. This omission introduces inaccuracies, particularly in the higher-order gravitational wave signals crucial for precise parameter estimation. Consequently, existing waveform templates may struggle to accurately represent real EMRI events, potentially leading to missed detections or misidentified source characteristics, especially as gravitational wave observatories strive to detect increasingly faint and compact systems where M/a₀ ≈ 10⁻⁵.
Accurate gravitational wave detection and precise estimation of black hole system parameters hinge on a comprehensive understanding of spacetime alterations caused by dark matter. Current models often simplify these effects, potentially obscuring subtle signals, particularly when analyzing extreme mass ratio inspirals. Achieving detectable signals at extremely high compactness – specifically, down to M/a_0 \approx 10^{-5} – demands a fully relativistic treatment that incorporates these dark matter-induced perturbations. Without this level of precision, the inferred masses, spins, and distances to these black hole systems may be significantly skewed, hindering efforts to test general relativity and probe the nature of dark matter itself. The ability to accurately model these intricate interactions is therefore paramount for maximizing the scientific return from current and future gravitational wave observatories.
Relativity: The Key to Modeling Dark Matter’s Influence
Newtonian gravity approximates gravitational effects as an instantaneous force between masses, which becomes insufficient when dealing with the strong gravitational fields present in and around Dark Matter halos. General Relativity, however, describes gravity as a geometric property of spacetime, caused by the presence of mass-energy; this framework is essential for accurately modeling the spacetime distortions induced by these halos. Specifically, the relativistic treatment accounts for gravitational self-potential, which is neglected in Newtonian calculations, and becomes significant at the high densities characteristic of Dark Matter halos. This leads to a more precise calculation of geodesic deviations and orbital dynamics within the halo’s influence, demonstrating the necessity of a relativistic approach for high-precision astrophysical modeling of these structures and the objects embedded within them.
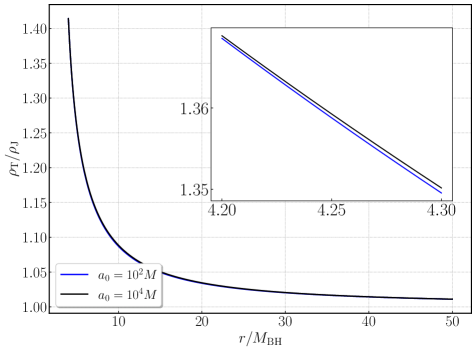
The Hernquist profile is employed to represent the three-dimensional density distribution of dark matter halos due to its analytical tractability and ability to reproduce key observational features. Defined as \rho(r) = \frac{\mathcal{M}}{2 \pi a^3} \frac{1}{(r/a)(1 + r/a)^3} , where \mathcal{M} is the total halo mass and a is the scale radius, this profile exhibits a centrally diverging density cusp and a characteristic fall-off at larger radii. The scale radius a defines the transition between the inner and outer density regimes, and is a key parameter in characterizing the halo’s structure. Compared to other profiles like the Navarro-Frenk-White (NFW) profile, the Hernquist profile offers a simpler mathematical form while still capturing the essential features of dark matter halo density distributions, facilitating analytical calculations within general relativistic frameworks.
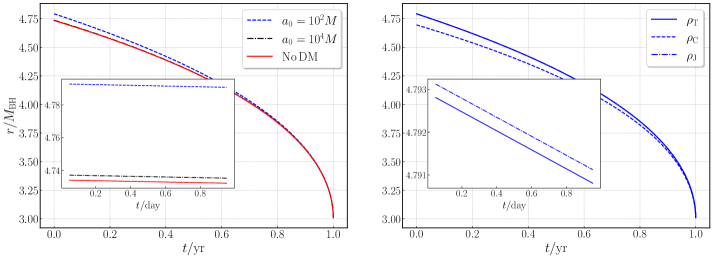
Calculations of compact object orbital evolution within dark matter halos demonstrate significant discrepancies when modeled using General Relativity versus Newtonian gravity. Specifically, at a mass-to-acceleration ratio of M/a_0 = 10^{-4}, fully relativistic density profiles (\rho_T) predict orbital behaviors differing by up to six orders of magnitude compared to those calculated using classical Newtonian density profiles (\rho_C). This difference arises from the accurate accounting of spacetime distortion by General Relativity, which is crucial for modeling strong gravitational fields within the dark matter halo and its influence on orbiting bodies. The magnitude of this deviation indicates that Newtonian approximations are insufficient for precise calculations in these environments.
Decoding the Universe: Constructing Gravitational Waveforms in Dark Matter Environments
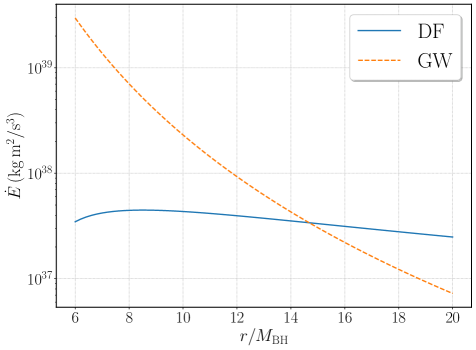
The Black Hole Perturbation Method is a fully relativistic technique used to calculate the gravitational wave fluxes emitted during the inspiral of a compact object – such as a neutron star or another black hole – into a Massive Black Hole. This method involves solving the Teukolsky equation, a perturbation equation describing the spacetime around a Kerr black hole, with appropriate boundary conditions to model the interaction with the surrounding environment. When applied to systems embedded within Dark Matter halos, the method accounts for the backreaction of the halo’s mass distribution on the spacetime geometry, thereby accurately quantifying the emitted GW energy and angular momentum. The resulting fluxes are crucial for constructing accurate waveform templates used in the detection and analysis of gravitational wave signals from these complex astrophysical systems.
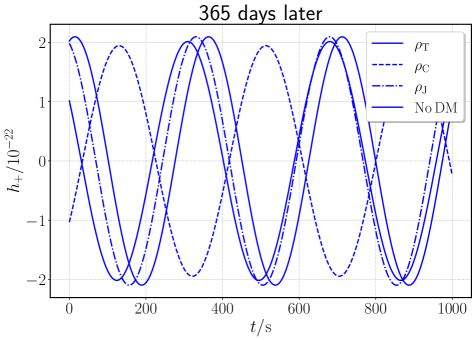
Post-adiabatic gravitational waveform generation incorporates relativistic effects stemming from the presence of a dark matter halo surrounding a massive black hole. This approach moves beyond simplified, non-relativistic treatments by accounting for the halo’s influence on spacetime geometry and, consequently, the emitted gravitational waves. Specifically, the methodology accurately models the dynamic response of the dark matter halo to the inspiraling compact object, which manifests as corrections to the standard quadrupole waveform. These corrections are crucial for generating waveforms that realistically represent the signal detectable by gravitational wave observatories, improving the accuracy of parameter estimation and astrophysical inference. The resulting waveforms represent a significant advancement in modeling gravitational wave events occurring within dark matter environments.
Accurate gravitational waveform models are critical for interpreting signals detected by gravitational wave observatories, enabling precise parameter estimation of binary systems. In scenarios involving compact objects inspiraling into massive black holes within dark matter halos, these waveforms must account for the halo’s relativistic effects to avoid systematic errors in data analysis. Simulations demonstrate that peak radial pressure ratios within the dark matter halo can reach approximately 0.01 for a halo scale radius of a_0 = 100M surrounding a black hole with mass M = 10^4M_\odot, highlighting the magnitude of the perturbation and the necessity of incorporating these effects into waveform generation for accurate modeling and information extraction.
The Signature of the Invisible: Validating and Quantifying Waveform Discrepancies
Waveform mismatch serves as a powerful metric for discerning the subtle imprints of dark matter on gravitational wave signals. By meticulously calculating gravitational waveforms both with and without the inclusion of dark matter halo effects around black holes, researchers can quantify the degree of difference between the two. This mismatch isn’t simply a qualitative observation; it’s a precise numerical value – currently estimated at a threshold of 0.0115 – that indicates whether a detected signal likely originates from a system influenced by dark matter. Essentially, the technique treats deviations from expected waveforms as fingerprints of dark matter, allowing scientists to statistically assess the detectability of these elusive halos and refine models of their distribution and properties. This rigorous approach transforms the search for dark matter from a speculative endeavor into a quantifiable scientific pursuit, leveraging the universe’s most dramatic events to probe one of its greatest mysteries.
Calculations concerning gravitational waveforms and the potential influence of dark matter require a well-defined spacetime framework, and this research utilizes the Schwarzschild metric as that foundational element. This metric describes the spacetime geometry around a non-rotating, spherically symmetric mass – effectively, a simplified model of a black hole. By building calculations upon this established solution to Einstein’s field equations, researchers can accurately model the expected gravitational waves emitted from binary black hole systems. Any deviations observed in real-world data, when compared against waveforms predicted using this Schwarzschild background, can then be rigorously analyzed as potential evidence for the presence of dark matter halos surrounding these massive objects, providing a crucial benchmark for signal detection and a robust basis for quantifying waveform discrepancies.
The ability to discern subtle distortions in gravitational wave signals offers a pathway to investigating the elusive nature of Dark Matter. Researchers have established a quantifiable threshold – a waveform mismatch of 0.0115 – that effectively differentiates between signals generated by binary black hole systems with and without the influence of Dark Matter halos. This level of precision allows for the assessment of how readily Dark Matter signatures can be detected within the complex data stream from gravitational wave observatories. Beyond simple detection, this methodology facilitates a refinement of existing models, providing a means to constrain the properties of Dark Matter itself and deepen the understanding of the environments surrounding these massive cosmic events. The quantifiable mismatch serves as a critical benchmark, enabling the systematic exploration of parameter space and the potential unveiling of new physics beyond the Standard Model.
A New Window into the Cosmos: Gravitational Waves and the Hunt for Dark Matter
The unprecedented sensitivity of gravitational wave detectors now offers a novel pathway to investigate the elusive nature of dark matter. These detectors, originally designed to observe ripples in spacetime caused by cataclysmic cosmic events, are proving capable of probing the subtle gravitational signatures of dark matter halos. By meticulously analyzing the distortions in gravitational waves as they traverse these halos, researchers can begin to constrain key properties, including the density and energy distribution of dark matter within them. This approach differs significantly from traditional methods, which rely on observing the effects of dark matter on visible matter; instead, it allows for a direct, albeit indirect, measurement of dark matter’s gravitational influence, potentially revealing insights into its composition and behavior at scales previously inaccessible. The technique promises to refine models of dark matter and deepen understanding of its role in the structure and evolution of the Universe.
To rigorously test theoretical predictions regarding dark matter’s influence on gravitational waves, researchers developed the Numerical Kludge – a computational tool designed to generate expected waveforms. This isn’t a traditional, high-precision simulation; rather, the Kludge efficiently produces approximate waveforms representing the subtle distortions gravitational waves might experience as they traverse dark matter halos. By comparing these generated signals with the data received from gravitational wave detectors, scientists can validate or refine their models of dark matter distribution and composition. The approach allows for rapid prototyping and exploration of a wide range of dark matter scenarios, effectively serving as a crucial bridge between theoretical predictions and observational data, and is demonstrably sensitive to halo compactness down to M/a₀ ≈ 10⁻⁵.
Recent research indicates gravitational wave detection offers a novel pathway to unraveling the mysteries of dark matter and the broader universe. The study demonstrates a surprising level of sensitivity, potentially allowing for the identification of dark matter structures with a compactness parameter as low as M/a₀ ≈ 10⁻⁵. This threshold suggests that even relatively diffuse dark matter halos could be detectable through their subtle influence on gravitational waves, providing a unique observational probe complementary to traditional astrophysical methods. The findings highlight the exciting possibility of mapping the distribution and properties of dark matter across vast cosmic distances, ultimately refining models of galaxy formation and the universe’s large-scale structure, and potentially revealing the fundamental nature of this elusive substance.
The study meticulously details how radial pressure within dark matter halos alters the gravitational waveforms emitted by extreme mass ratio inspirals. This isn’t merely a refinement of existing models; it’s an acknowledgement that any attempt to quantify the universe is riddled with assumptions about unobservable forces. As Mary Wollstonecraft observed, “The mind should not be suffered to stagnate; it should be perpetually at work.” This research exemplifies that principle – continually testing and refining assumptions about dark matter distribution, acknowledging that a static understanding risks obscuring the subtle, yet crucial, relativistic effects influencing gravitational wave detection. The insistence on accounting for these nuances isn’t about achieving ‘objective’ accuracy, but about minimizing the inevitable distortions inherent in any measurement of a complex system.
Where Do We Go From Here?
The exercise, as always, reveals the limits of the assumptions. This work demonstrates the necessity of incorporating relativistic effects and radial pressure profiles when modeling dark matter distributions around extreme mass ratio inspirals. It is a technical improvement, certainly – waveform models will be marginally less wrong. However, it simultaneously highlights a far larger problem: the halos themselves. The standard assumptions regarding dark matter density and distribution remain, for the moment, a convenient fiction. Should future gravitational wave detectors fail to observe the predicted signal strength, the first instinct will be to refine the models. The more honest approach will be to question the underlying premises.
The immediate path forward involves extending these calculations to more complex dark matter models – self-interacting dark matter, fuzzy dark matter, and whatever exotic possibilities are yet to be proposed. Each addition, however, introduces further parameters, further degeneracies, and further opportunities for the models to accommodate any observation, or lack thereof. It is a useful reminder that fitting a model to data does not necessarily reveal truth; it simply demonstrates the model’s flexibility.
Ultimately, the true test will not be whether the waveforms can be accurately modeled, but whether the observed inspiral events exhibit anomalies that cannot be explained by standard general relativity and collisionless dark matter. It’s a low probability outcome, to be sure, but the history of physics suggests that the most interesting discoveries often lie at the edges of what is considered impossible. And if everything fits perfectly? Then one must suspect, with quiet resignation, that something fundamental has been overlooked.
Original article: https://arxiv.org/pdf/2602.12022.pdf
Contact the author: https://www.linkedin.com/in/avetisyan/
See also:
- Best Controller Settings for ARC Raiders
- Bitcoin’s Mysterious Millionaire Overtakes Bill Gates: A Tale of Digital Riches 🤑💰
- Gwen Stefani Details “Blessing” of Her Holidays With Blake Shelton
- 10 X-Men Batman Could Beat (Ranked By How Hard It’d Be)
- Wizards of the Coast Unveil New Dungeons & Dragons Game Warlock
- Stephen Colbert Jokes This Could Be Next Job After Late Show Canceled
- The $35 Million Crypto Crime: Ex-CFO’s Greed Backfires Spectacularly
- Arnold Schwarzenegger’s Son Patrick Details Growing Up on Movie Sets
- How to Froggy Grind in Tony Hawk Pro Skater 3+4 | Foundry Pro Goals Guide
- How to Get to Heaven from Belfast soundtrack: All songs featured
2026-02-15 18:42