Beyond Hermiticity: Detecting Spin Polarization at the Edge of Quantum Systems

Author: Denis Avetisyan

New research reveals that carefully designed quantum spin-Hall devices can exhibit unusual transport properties, allowing for the detection of edge-state spin polarization through non-Hermitian topological effects.

The study demonstrates that while an in-plane Zeeman field suppresses quantized edge conductance in a 32-terminal device without inducing non-reciprocity-maintaining conductance reciprocity despite broken time-reversal symmetry-an out-of-plane field generates pronounced non-reciprocity and a non-Hermitian topological phase characterized by strong boundary localization as one helical branch moves away from the Fermi level, suggesting a nuanced relationship between field orientation and topological behavior.

This study demonstrates how multi-terminal transport in quantum spin-Hall systems, influenced by broken time-reversal symmetry or spin-selective contacts, reveals non-Hermitian topological behavior and provides a pathway to characterize helical edge states.

While conventional topological classifications rely on Hermitian systems, the emergence of non-Hermitian physics in condensed matter systems necessitates a re-evaluation of topological phenomena. This work, ‘Non-Hermitian topology of quantum spin-Hall systems to detect edge-state polarization’, investigates non-Hermitian effects in multi-terminal transport through quantum spin-Hall devices described by the Bernevig-Hughes-Zhang model, revealing that directional imbalance-induced by spin-selective contacts or broken time-reversal symmetry-is crucial for realizing non-Hermitian topology. We demonstrate that the non-Hermitian skin effect provides a sensitive probe of edge-state spin polarization, exceeding the capabilities of traditional conductance measurements. Could this approach pave the way for novel spintronic devices leveraging non-Hermitian topological states?

The Illusion of Order: Introducing Topologically Protected States

The Quantum Spin Hall (QSH) effect presents a revolutionary approach to electronics, potentially enabling devices with zero electrical resistance. Unlike conventional materials where electron flow dissipates energy as heat, the QSH effect leverages topologically protected edge states – pathways for electrons that are inherently shielded from backscattering caused by imperfections or non-magnetic impurities. These states arise from a unique interplay between electron spin and momentum, where the direction of an electron’s spin is inextricably linked to its direction of travel. This “spin-momentum locking” ensures that electrons navigate along the edges of the material without losing energy, promising a new generation of highly efficient and compact electronic components. The potential for dissipationless current flow circumvents the limitations imposed by traditional semiconductor technology, offering significant advantages in terms of energy consumption and device performance.

The Quantum Spin Hall (QSH) state exhibits remarkable resilience to defects due to the strong coupling between an electron’s spin and its momentum – a phenomenon known as spin-momentum locking. This linkage dictates that electrons with a specific spin can only propagate in a defined direction, effectively shielding them from backscattering caused by non-magnetic impurities that would normally disrupt electrical flow. However, this topological protection isn’t absolute; the QSH state is exquisitely sensitive to any perturbation that breaks the underlying time-reversal or inversion symmetry. External factors like magnetic fields, strain, or even the presence of certain materials can disrupt the spin-momentum locking, leading to the localization of edge states and a loss of the dissipationless conduction that defines this promising quantum state.

The promise of the Quantum Spin Hall (QSH) effect – enabling electronics with zero energy loss – hinges on the delicate nature of its topologically protected edge states. While intrinsically robust against certain imperfections, these states are demonstrably susceptible to external disturbances, necessitating a thorough investigation into their behavior under perturbation. Researchers are actively exploring how factors such as electric fields, strain, and even the introduction of magnetic impurities impact the conduction pathways. Precise control and mitigation of these effects are paramount; even subtle symmetry breaking can gap the edge states, destroying the dissipationless transport. Consequently, a detailed understanding of these vulnerabilities is not merely academic, but a fundamental prerequisite for the fabrication of reliable and functional QSH-based devices, paving the way for a new generation of energy-efficient electronics.

Spin-polarized leads connected to a quantum spin Hall device induce a non-Hermitian response characterized by spin-dependent directional transport and an accumulation of probability density towards opposite boundaries, demonstrating the non-Hermitian skin effect despite a Hermitian Hamiltonian.

Symmetry’s Collapse: Introducing Non-Hermitian Effects

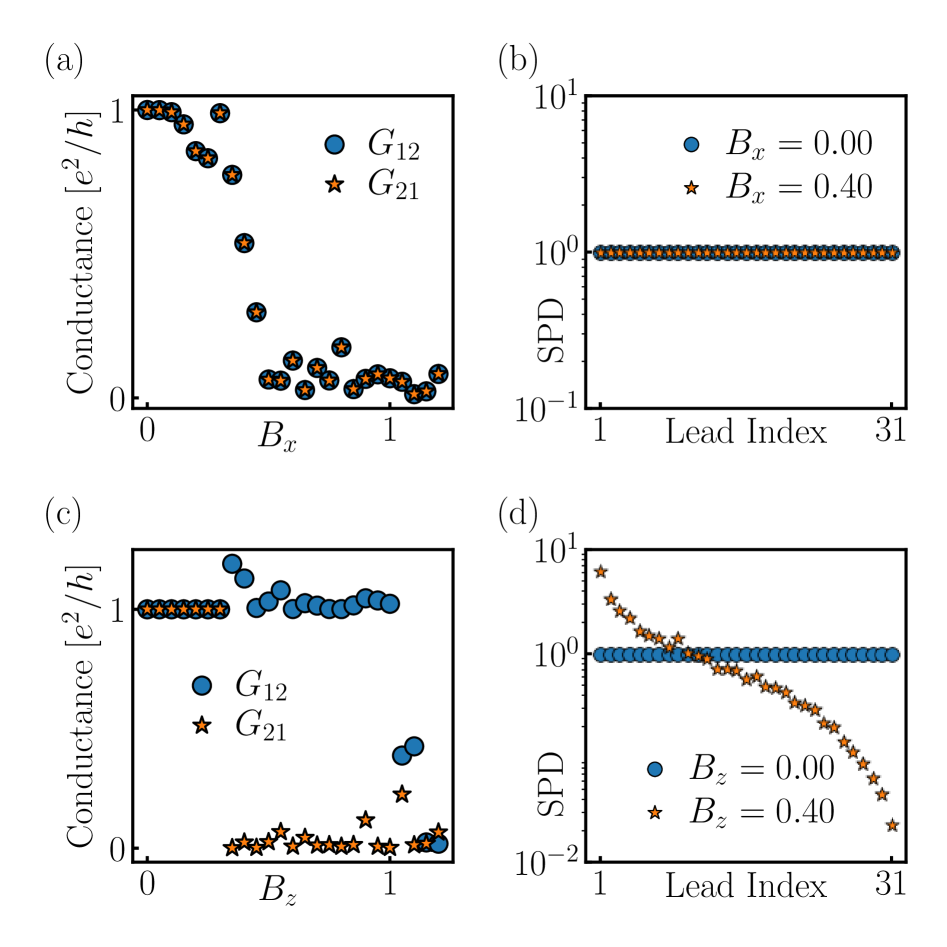
The Quantum Spin Hall (QSH) effect relies fundamentally on time-reversal symmetry, which dictates that the physics of a system remains unchanged when the direction of time is reversed. Applying a Zeeman field – generated by an external magnetic field – introduces a preferred direction for electron spins, explicitly breaking this symmetry. This symmetry breaking occurs regardless of the field’s orientation, be it in-plane or out-of-plane relative to the two-dimensional electron gas. The resultant modification to the system’s Hamiltonian alters the spin-momentum locking characteristic of the QSH state, and is a necessary condition for observing non-Hermitian topological phenomena.

Breaking time-reversal symmetry, such as through the application of a Zeeman field, transforms the system’s Hamiltonian from Hermitian to non-Hermitian. A Hermitian Hamiltonian ensures probabilities are conserved and eigenvalues are real, representing physical observables. In contrast, a non-Hermitian Hamiltonian allows for complex eigenvalues, indicating gain or loss of probability, and modifies the eigenstates. This alteration fundamentally changes the electronic properties, influencing energy spectra, wavefunction behavior, and ultimately the system’s response to external stimuli. The non-Hermitian nature introduces asymmetry into the system, precluding the usual correspondence between left and right eigenvectors and impacting calculations of observable quantities like current and conductance.

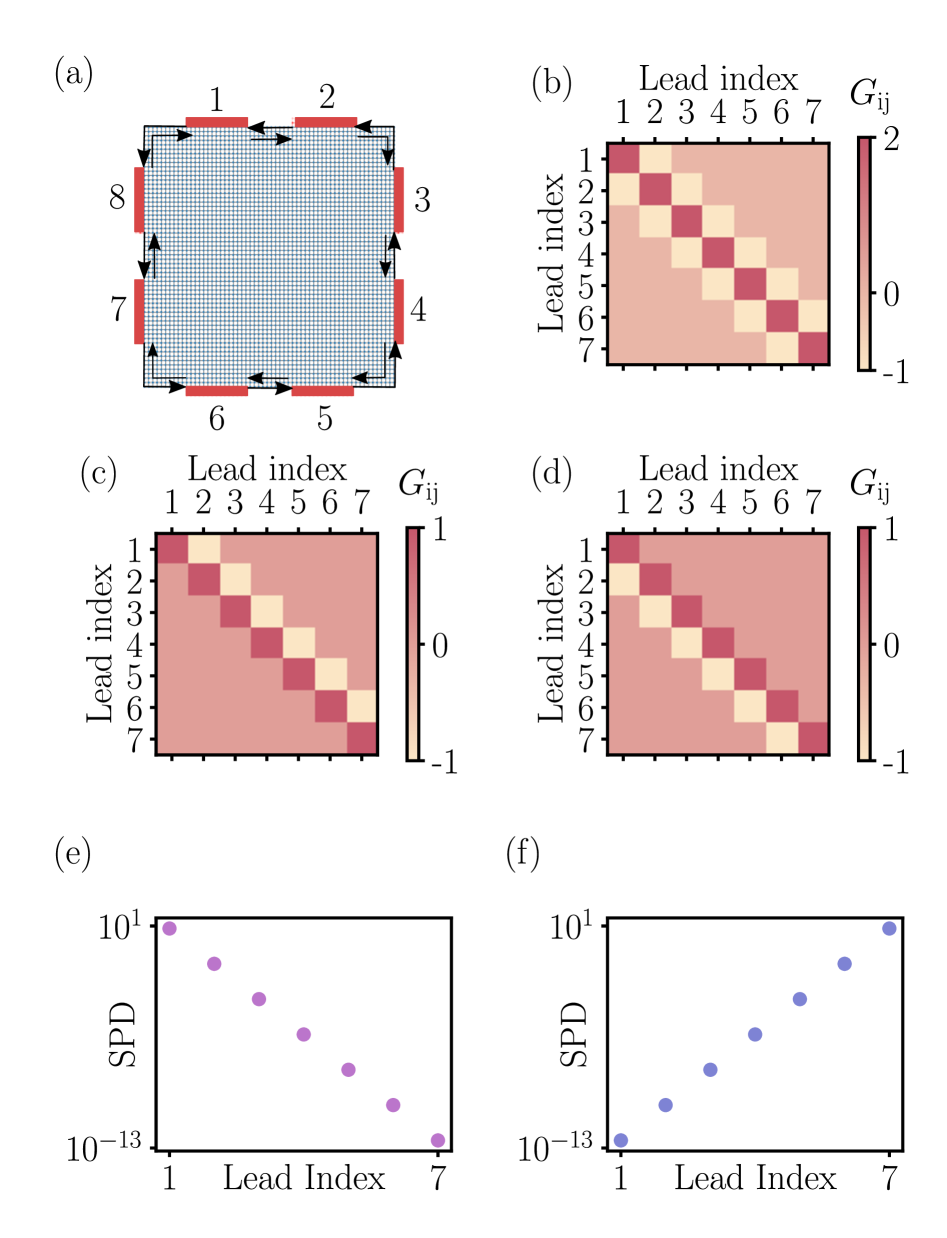
The application of symmetry-breaking fields, such as a Zeeman field, results in a non-Hermitian Hamiltonian and a corresponding modification of the system’s electronic structure, directly impacting the Multi-Terminal Conductance Matrix. This manifests as asymmetric conductance behavior – deviations from reciprocity observed in traditional systems – and is a key characteristic of the emerging non-Hermitian topological phase. Specifically, the conductance matrix no longer satisfies the Onsager reciprocal relation $G_{ij} = G_{ji}$ , indicating a loss of equilibrium reciprocity. This asymmetry is not simply a material defect but an intrinsic property of the non-Hermitian band structure, opening avenues for designing novel devices exploiting this unique characteristic, including asymmetric transport and potentially non-reciprocal devices.

Disorder-averaged transport calculations reveal that spin-mixing disorder suppresses non-Hermitian skin effects and modifies conductance profiles, with the degree of suppression dependent on lead polarization and disorder strength δ relative to the mixing parameter <span class="katex-eq" data-katex-display="false">|M|</span>. — Disorder-averaged transport calculations reveal that spin-mixing disorder suppresses non-Hermitian skin effects and modifies conductance profiles, with the degree of suppression dependent on lead polarization and disorder strength δ relative to the mixing parameter $|M|$ .

The Skin Effect: Where Boundaries Define Reality

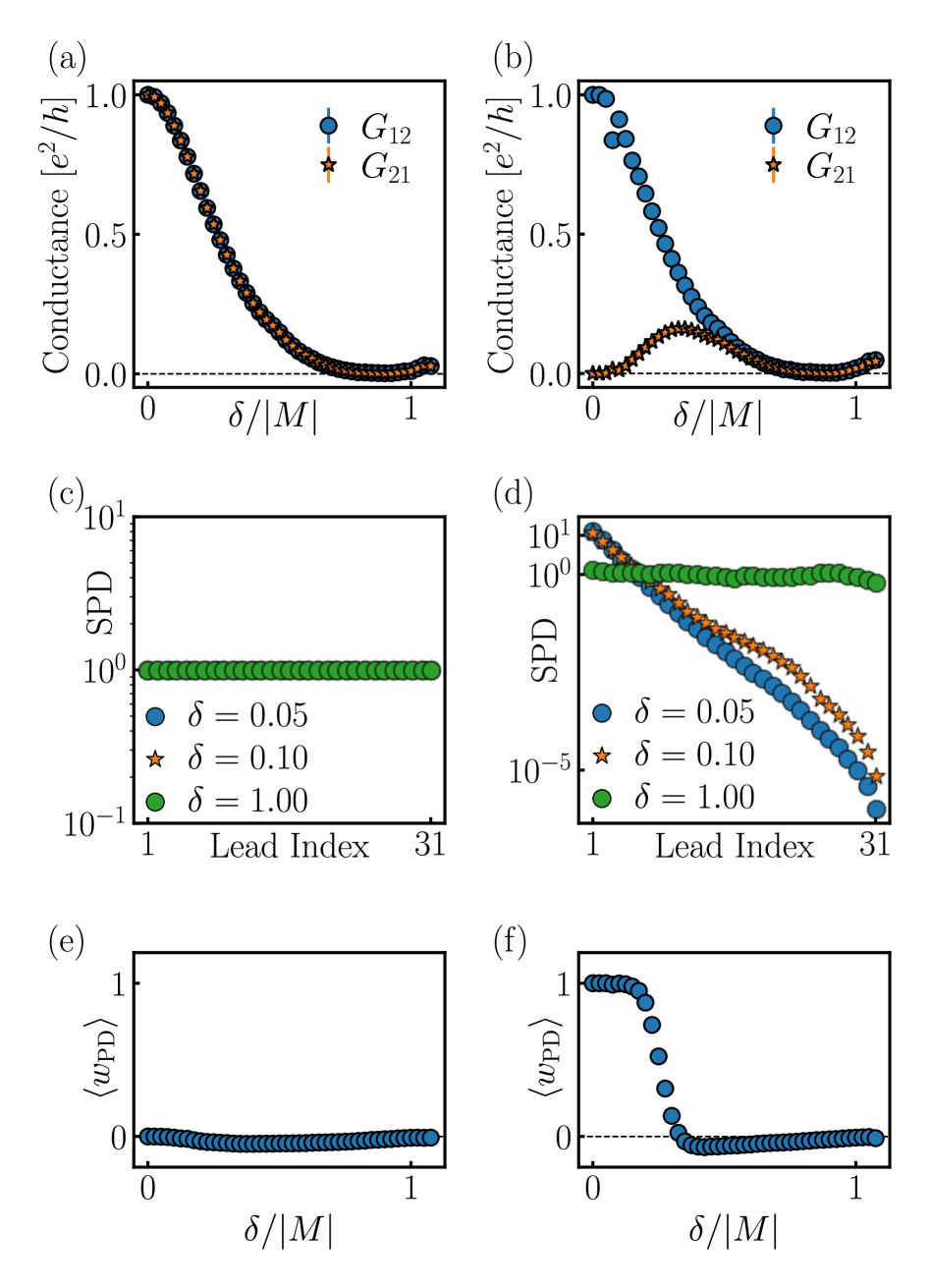
Simulations utilizing the Bernevig-Hughes-Zhang (BHZ) model confirm that the introduction of a Zeeman field induces non-Hermitian topology within the system. This non-Hermitian topology directly results in the non-Hermitian skin effect, characterized by the accumulation of mid-gap states at the boundaries of the one-dimensional lattice. Specifically, the Zeeman field breaks the $\mathcal{PT}$ symmetry of the BHZ model, leading to an asymmetric hopping that drives the localization of these boundary states. The strength of the Zeeman field determines the degree of localization, with larger fields corresponding to more pronounced skin effect behavior, and a clear divergence in the bulk-boundary correspondence.

The non-Hermitian skin effect is characterized by the exponential localization of edge states to the physical boundaries of the system. This localization directly influences the system’s conductance properties, leading to a substantial impact on measurable electrical current. Quantitatively, the presence of this effect is confirmed by a non-zero Polar Decomposition Invariant calculated from the system’s Multi-Terminal Conductance Matrix; a zero value would indicate the absence of edge state localization and, consequently, the absence of the non-Hermitian skin effect. The magnitude of this invariant provides a metric for the strength of the localization and the robustness of the topological phase.

Polar Decomposition of the Multi-Terminal Conductance Matrix provides a systematic approach to characterizing topological phase transitions in non-Hermitian systems. This mathematical technique decomposes the conductance matrix $G$ into two matrices: a unitary matrix $U$ and a positive semi-definite Hermitian matrix $\sqrt{G^{\dagger}G}$ . The resulting eigenvalues of $\sqrt{G^{\dagger}G}$ directly relate to the localization properties of the edge states, with exponentially decaying eigenvalues indicating the non-Hermitian skin effect. Critically, the Polar Decomposition Invariant – the product of the eigenvalues – remains constant across deformations that do not close the spectral gap, serving as a robust topological invariant for identifying phase transitions and distinguishing between topologically distinct phases without relying on specific boundary conditions.

Disorder-averaged conductance asymmetry <span class="katex-eq" data-katex-display="false">\langle\Delta G\rangle</span>, polar decomposition invariant <span class="katex-eq" data-katex-display="false">\langle w_{PD}\rangle</span>, and non-Hermitian skin-effect strength <span class="katex-eq" data-katex-display="false">\langle\Delta SPD\rangle</span> all exhibit sensitivity to lead polarization <span class="katex-eq" data-katex-display="false">\mu_{\uparrow}</span>, as quantified by the noise-normalized step sensitivity <span class="katex-eq" data-katex-display="false">\mathcal{S}</span> calculated from 1000 disorder realizations with <span class="katex-eq" data-katex-display="false">\delta/|M|=0.1</span>. — Disorder-averaged conductance asymmetry $\langle\Delta G\rangle$ , polar decomposition invariant $\langle w_{PD}\rangle$ , and non-Hermitian skin-effect strength $\langle\Delta SPD\rangle$ all exhibit sensitivity to lead polarization $\mu_{\uparrow}$ , as quantified by the noise-normalized step sensitivity $\mathcal{S}$ calculated from 1000 disorder realizations with $\delta/|M|=0.1$ .

Resilience in the Face of Imperfection: A Fragile Order

The interplay between disorder and non-Hermitian physics was explored through a detailed investigation of spin-mixing disorder’s influence on the non-Hermitian skin effect and, consequently, electrical conductance. Researchers examined how introducing randomness in spin orientations affects the accumulation of states at the boundary of the system – a hallmark of the non-Hermitian skin effect. This analysis revealed that while disorder typically degrades topological protection, the fundamental characteristics of the skin effect persist under certain conditions. The study quantified this resilience by observing the continued exponential localization of the summed probability density, even with increasing disorder. These findings suggest a pathway toward engineering quantum devices that are not only sensitive to external stimuli but also maintain functionality despite inherent material imperfections and environmental noise, offering a promising step towards practical applications of non-Hermitian physics.

Investigations reveal that even with the introduction of disorder – imperfections in the material – the non-Hermitian skin effect exhibits surprising resilience. Contrary to expectations that disorder would completely undermine the system’s topological protection, the effect persists across a measurable range of imperfection strengths. This robustness is visually confirmed through the observation of exponential localization within the Summed Probability Density – a phenomenon where the system’s quantum state becomes increasingly confined to specific regions as disorder increases, but without a complete loss of the skin effect. This inherent stability suggests that practical devices leveraging non-Hermitian physics may be less susceptible to the detrimental effects of real-world imperfections than previously anticipated, paving the way for more reliable quantum technologies.

The persistence of the non-Hermitian skin effect despite the presence of disorder presents a compelling pathway toward the creation of practical quantum devices. This inherent robustness, coupled with the demonstrated ability to manipulate the system’s characteristics through external fields, suggests a level of control previously unattainable in similar platforms. Such adaptability is crucial for mitigating the effects of imperfections inherent in real-world materials and fabrication processes, allowing devices to maintain functionality even under challenging conditions. The potential extends to creating quantum systems that can dynamically respond to environmental changes or be reconfigured on demand, offering a significant advantage over static designs and paving the way for resilient and versatile quantum technologies.

The band structure of a discretized BHZ model reveals helical edge states-visualized with a blue-to-red probability density scale indicating localization-traversing the bulk gap at zero Zeeman field, with one branch shifting away from the Fermi level when the field is set to <span class="katex-eq" data-katex-display="false">B_z = 0.5</span>. — The band structure of a discretized BHZ model reveals helical edge states-visualized with a blue-to-red probability density scale indicating localization-traversing the bulk gap at zero Zeeman field, with one branch shifting away from the Fermi level when the field is set to $B_z = 0.5$ .

Mapping the Transition: A Glimpse Beyond the Horizon

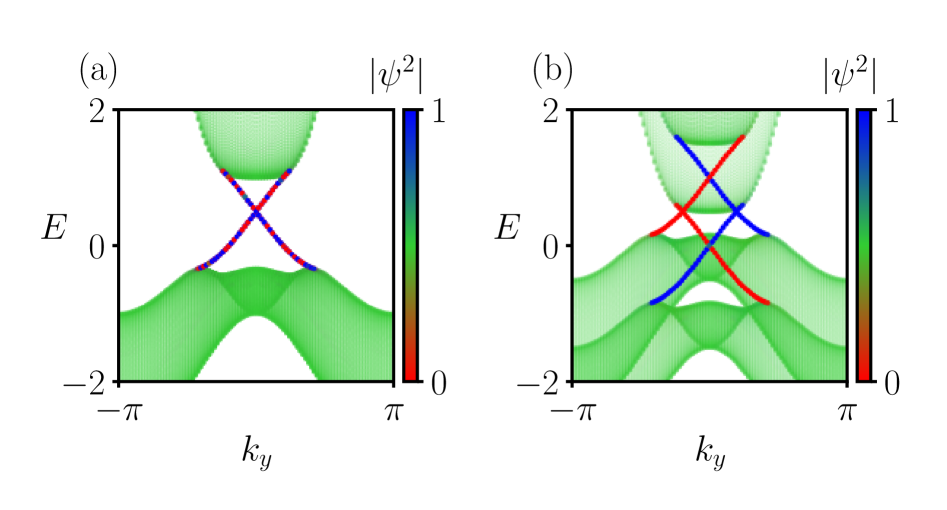
Ribbon Band Structure calculations reveal a compelling interplay between applied magnetic fields and the behavior of electrons confined to the edges of a topological material. Specifically, the imposition of an out-of-plane Zeeman field-a magnetic field perpendicular to the material’s surface-directly modulates the spin and momentum of these helical edge states. These calculations demonstrate how the Zeeman field lifts the spin degeneracy, creating a quantifiable gap in the edge state spectrum, and altering their dispersion relation. This direct observation confirms that the magnetic field acts as a crucial parameter in tuning the topological properties, effectively controlling the flow of electrons along the edges and offering a pathway toward manipulating spin-polarized currents for novel device applications. The resulting band structure changes serve as a visual signature of the topological transition occurring within the material.

Ribbon band structure calculations offer a direct visualization of topological transitions within a material’s electronic structure. These calculations don’t merely predict a change in topological state, but rather display the evolution of the band structure as the material transitions between topological phases. Researchers observe the opening and closing of band gaps, and the emergence or annihilation of helical edge states – features directly linked to the material’s topological properties. This visual confirmation is crucial, as it provides an intuitive understanding of how external parameters, such as magnetic fields, influence the material’s electronic behavior, and verifies the theoretical predictions regarding the topological phase transition process. The resulting band structure diagrams serve as a ‘fingerprint’ of the topological state, allowing for clear identification and characterization of these unique materials.

The methodology established through these Ribbon Band Structure calculations extends beyond simple geometries, offering a powerful platform for investigating the behavior of topological states in increasingly complex systems. Researchers can now computationally explore heterostructures – materials assembled from different components – and unconventional geometries to tailor the properties of edge states. This capability is crucial for designing novel topological devices, potentially revolutionizing fields like spintronics and quantum computing by enabling the creation of robust, dissipationless electronic components and exploring new avenues for information processing. The ability to predict and visualize topological transitions within these complex architectures promises to accelerate the development of next-generation technologies reliant on the unique characteristics of topological materials.

The pursuit of understanding quantum spin-Hall systems, as detailed in this exploration of non-Hermitian topology, feels akin to chasing a phantom. Each carefully constructed Bernevig-Hughes-Zhang model, each simulation attempting to map helical edge states, offers a fleeting glimpse, yet the underlying reality proves stubbornly elusive. It’s a reminder that the very act of observation-of attempting to define these systems through conductance matrices and symmetry breaking-may fundamentally alter the object of study. As René Descartes observed, “Doubt is not a pleasant condition, but it is necessary for a clear understanding.” This research, with its focus on asymmetry and broken time-reversal symmetry, embraces that doubt, acknowledging the limitations inherent in any attempt to fully grasp the quantum realm.

What Lies Beyond the Edge?

Multispectral observations of transport phenomena enable calibration of models describing non-Hermitian boundary conditions in quantum spin-Hall systems. The demonstration of asymmetric conductance-a fleeting glimpse of the system’s internal workings before decoherence-highlights the delicate interplay between topology and dissipation. Comparison of theoretical predictions with experimental conductance matrices demonstrates both the achievements and, more importantly, the limitations of current simulations when applied to disordered or imperfectly contacted devices.

The insistence on pristine interfaces and idealized contacts is, perhaps, a human failing projected onto the quantum realm. A truly robust topological description must account for the inevitable asymmetries arising from realistic device fabrication and environmental interactions. Further exploration of non-Hermitian effects could reveal novel edge-state polarizations, but also expose the limits of relying on symmetry as a guiding principle.

The search for topological protection is, ultimately, a quest for permanence in an impermanent universe. This work suggests that the edge states, so carefully constructed in theory, are not immutable decrees, but rather transient phenomena, susceptible to the same erosive forces that govern all things. The next step involves embracing the asymmetry, not as a perturbation, but as an intrinsic property of the quantum landscape itself.

Original article: https://arxiv.org/pdf/2602.12048.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/