Beyond the Usual: Observing Fractional Fermi Seas in a Quantum Gas

by

Author: Denis Avetisyan

Researchers have experimentally created and observed fractional Fermi seas – a novel quantum state of matter – within a one-dimensional Bose gas, opening new avenues for understanding interacting quantum systems.

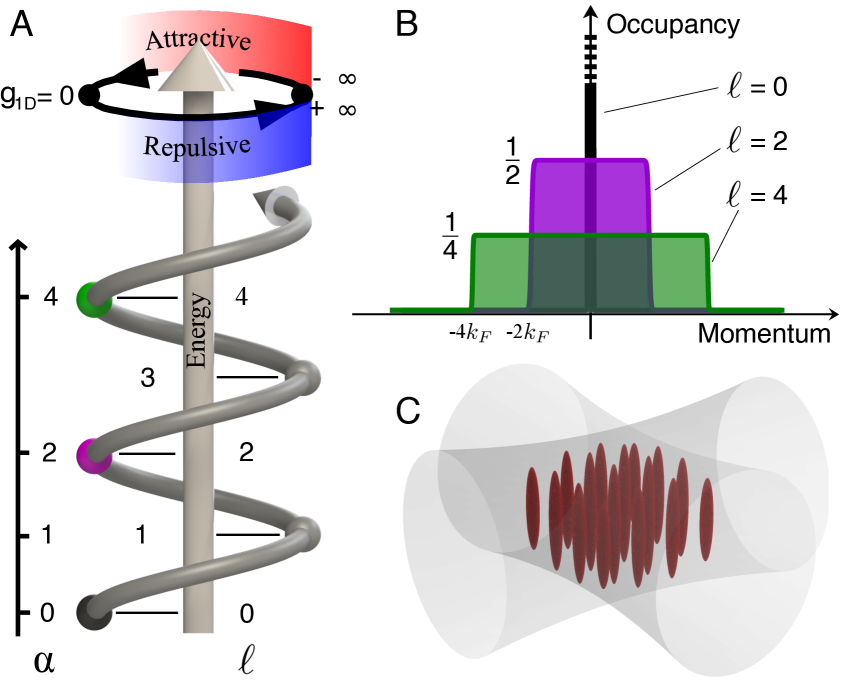
The emergence of fractional flux strings-manifestations of topology in a one-dimensional Bose gas-becomes apparent as the system transitions from repulsive to attractive interactions, passing through a singular point where these strings materialize at momenta dictated by a charge parameter, a phenomenon realized both theoretically and experimentally via arrays of vertically oriented atomic tubes within a two-dimensional optical lattice.
The emergence of fractional flux strings-manifestations of topology in a one-dimensional Bose gas-becomes apparent as the system transitions from repulsive to attractive interactions, passing through a singular point where these strings materialize at momenta dictated by a charge parameter, a phenomenon realized both theoretically and experimentally via arrays of vertically oriented atomic tubes within a two-dimensional optical lattice.

The study demonstrates the realization of fractional Fermi seas through interaction-ramping cycles, confirmed by the observation of Friedel oscillations in momentum distributions.

The Pauli exclusion principle, a cornerstone of quantum mechanics, dictates the occupancy of quantum states, yet theoretical extensions predict exotic states beyond its confines. This work, ‘Realization of fractional Fermi seas’, reports the experimental observation of these fractional states in a one-dimensional Bose gas, achieved through precisely controlled interaction ramping cycles. Specifically, the researchers demonstrate the emergence of fractional Fermi seas-characterized by uniform but fractional occupancies-evidenced by the detection of Friedel oscillations in momentum distributions. Could these stabilized, non-standard states offer new insights into quantum thermodynamics and unlock applications in quantum information technologies?

The Illusion of Simplicity: Beyond Standard Models

The conventional frameworks of fermionic and bosonic statistics, while remarkably successful in describing many materials, encounter limitations when applied to systems where interactions between constituent particles are exceptionally strong. In these strongly correlated many-body systems, the simple picture of particles each occupying a single quantum state breaks down, hindering accurate predictions of material properties. This failure stems from the inability of these established statistical methods to account for the complex entanglement and collective behavior that emerge from intense interactions. Consequently, phenomena observed in exotic materials-such as high-temperature superconductors and quantum spin liquids-remain poorly understood, demanding new theoretical approaches that move beyond the constraints of traditional particle statistics and can accurately model the intricate interplay between particles.

The concept of Fractional Fermi Seas proposes a radical departure from traditional understandings of how particles populate quantum states. In conventional systems, each fermion – a particle obeying the Pauli exclusion principle – occupies a single quantum state. However, within a Fractional Fermi Sea, strong interactions effectively allow particles to ‘fractionalize’ their occupancy, spreading across multiple states as if they were partial residents of each. This isn’t a physical splitting of the particle, but rather an emergent behavior arising from collective interactions. This phenomenon unlocks the potential to explore exotic states of matter beyond the reach of conventional Fermi-Dirac statistics, potentially revealing novel phases characterized by unique electronic and magnetic properties. \text{Instead of a single occupation number, each state is populated by a fraction.} The implications are significant, offering a pathway to understand strongly correlated materials and potentially enabling the design of materials with unprecedented functionalities.

The proposition of Fractional Fermi Seas fundamentally disrupts established understandings of matter’s organization, suggesting that conventional descriptions of quantum states are insufficient for strongly interacting systems. This isn’t merely a refinement of existing models, but a departure that anticipates entirely new phases of matter – states exhibiting properties not predicted by traditional fermionic or bosonic statistics. These emergent properties could manifest as novel superconductivity, unconventional magnetism, or exotic topological states, potentially revolutionizing materials science and condensed matter physics. The ability to engineer and observe these fractionalized states promises a deeper understanding of quantum entanglement and collective behavior, opening avenues for technological advancements based on principles beyond the standard model.

Investigating Fractional Fermi Seas demands the development of both advanced theoretical frameworks and novel experimental techniques. Current methodologies, designed for systems obeying conventional statistics, struggle to accurately model the complex interactions and emergent behavior predicted by this new phase of matter. Researchers are actively pursuing extensions to existing many-body theories, such as density functional theory and quantum Monte Carlo simulations, to account for the fractionalization of fermionic states. Simultaneously, experimental probes capable of resolving the subtle signatures of these systems are crucial; this includes high-resolution angle-resolved photoemission spectroscopy to directly observe the modified electronic structure, as well as precision measurements of transport properties and thermodynamic quantities. The ability to manipulate and characterize these exotic states will not only validate theoretical predictions but also potentially pave the way for harnessing their unique characteristics in future technological applications, requiring a concerted effort across multiple disciplines to unlock the full potential of Fractional Fermi Seas.

Experimental momentum distributions of a Bose gas, closely matching both GHD simulations (accounting for <span class="katex-eq" data-katex-display="false">5\text{ nK}</span> thermal fluctuations) and Thomas-Fermi predictions for <span class="katex-eq" data-katex-display="false">\ell = 2</span> and <span class="katex-eq" data-katex-display="false">\ell = 4</span>, confirm the presence of finite-size scaling (FFS) as evidenced by the first-order correlation function shown in panels (B) and (C).
Experimental momentum distributions of a Bose gas, closely matching both GHD simulations (accounting for 5\text{ nK} thermal fluctuations) and Thomas-Fermi predictions for \ell = 2 and \ell = 4, confirm the presence of finite-size scaling (FFS) as evidenced by the first-order correlation function shown in panels (B) and (C).

The Laboratory of the Infinitesimal: Ultracold Cesium as a Probing Ground

Ultracold cesium gas serves as a versatile experimental platform for investigating fractional Fermi seas due to its high degree of controllability. By employing laser cooling and trapping techniques, cesium atoms are reduced to temperatures on the order of nanokelvins, minimizing thermal disturbances and allowing for precise control over atomic interactions. This control is achieved through manipulation of the atomic density and the application of external magnetic fields. The resulting system allows researchers to explore many-body physics in a regime where interactions are dominant and quantum effects are pronounced, facilitating the study of emergent phenomena in strongly correlated systems. The use of cesium, specifically its \text{}^{133}\text{Cs} isotope, offers advantages in terms of laser wavelengths and scattering properties, further enhancing experimental precision.

Feshbach resonance is a technique used to manipulate the scattering length between ultracold atoms by applying an external magnetic field. This control is achieved by aligning the magnetic field to match a specific energy level where a bound molecular state merges with the continuum of free atoms. By sweeping the magnetic field near this resonance, the effective interaction strength between the atoms can be continuously tuned from weakly attractive to strongly attractive or even repulsive. This tunability allows for the creation of strongly correlated states, where atomic interactions dominate the system’s behavior, and is critical for investigating many-body physics phenomena such as the formation of Bose-Einstein condensates and the emergence of novel quantum phases.

Optical lattices, created by interfering laser beams, provide a periodic potential that confines the cesium atoms to discrete lattice sites, effectively controlling the system’s dimensionality and enabling studies in lower dimensions. Confinement-induced resonance (CIR) arises when the harmonic trapping frequency of the optical lattice becomes comparable to the scattering length of the interatomic interactions. This leads to a significant enhancement of the effective interaction strength, allowing researchers to tune the system towards strongly correlated regimes and explore novel quantum phenomena. By manipulating the lattice depth and trapping frequencies, the dimensionality of the system can be adjusted, transitioning from three-dimensional bulk behavior to one- or two-dimensional confinement, and influencing the collective behavior of the fermionic atoms.

The observation of fractional Fermi seas requires stringent experimental control over ultracold cesium gas. Specifically, these systems are cooled to a one-dimensional temperature of 5 nanokelvin to minimize thermal fluctuations that would obscure the emergent fractionalized behavior. This low temperature, combined with techniques like Feshbach resonance and optical lattices, allows researchers to precisely tailor interatomic interactions and effectively realize the strong correlation parameters predicted by theoretical models of fractional Fermi liquids. Maintaining these conditions enables the isolation and study of the unique quantum states associated with fractionalization, where fermionic particles effectively behave as non-integer quantum numbers, a phenomenon not observed in conventional materials.

Atomic loss measurements reveal irreversible interaction cycles, with the system losing atoms during attractive phases <span class="katex-eq" data-katex-display="false">g_{1D}</span> and exhibiting a sharp energy decrease due to negative binding energy as confirmed by GHD simulations.
Atomic loss measurements reveal irreversible interaction cycles, with the system losing atoms during attractive phases g_{1D} and exhibiting a sharp energy decrease due to negative binding energy as confirmed by GHD simulations.

Mapping the Many: Theoretical Frameworks for Correlation

The Lieb-Liniger model is a mathematically solvable model describing the dynamics of interacting bosons confined to one spatial dimension. It utilizes a Hamiltonian incorporating a two-body contact interaction, parameterized by the interaction strength ‘c’. This model exhibits a unique phase diagram, transitioning from a Bose-Einstein condensate for small ‘c’ to a Tonks-Girardeau gas-a realization of free fermions-at larger values. Crucially, the model’s solutions demonstrate a direct correspondence to the physics of fractional Fermi seas, where the bosonic system can be mapped onto a system of non-interacting fermions with fractional occupation numbers; specifically, the bosonic wavefunction can be expressed as a determinant of fermionic operators, linking the many-body problem to single-particle fermionic behavior. This connection allows for analytical calculations of correlation functions and provides insights into the emergent low-energy physics of strongly correlated one-dimensional bosonic systems.

Holonomy cycles, derived from the Yang-Baxter equation, provide a systematic approach to constructing and characterizing excited states within the Lieb-Liniger model. These cycles, representing closed loops in the space of particle configurations, map to transfer matrix eigenvectors and directly yield the energy and other quantum numbers of the corresponding states. Specifically, tracing these cycles around different types of impurities or defects effectively generates a complete basis for the many-body Hilbert space, enabling the calculation of dynamical correlation functions and response functions. This method bypasses the need for direct diagonalization of the Hamiltonian, which becomes computationally intractable for larger system sizes, and offers a means to explore the system’s behavior under external perturbations and time evolution, revealing key insights into its dynamic properties and non-equilibrium behavior.

Tomonaga-Luttinger Liquid (TLL) theory describes the low-energy behavior of interacting fermionic or bosonic systems confined to one dimension. Unlike Fermi liquid theory which characterizes interacting systems in higher dimensions, TLL theory predicts that the elementary excitations are no longer quasiparticles with a well-defined momentum and lifetime, but rather collective modes consisting of fractionalized excitations – spinons and holons. This leads to a power-law decay of correlation functions, with exponents determined by the interaction strength, differing fundamentally from the exponential decay observed in Fermi liquids. Specifically, the theory predicts a velocity v_F for these excitations which is renormalized by interactions, and a power-law dependence of the density of states at the Fermi level, \rho(\epsilon) \propto \epsilon^{K-1}, where K is the Luttinger parameter quantifying the strength of interactions. These emergent properties dictate the system’s transport and response characteristics, notably exhibiting a lack of a quasiparticle residue at the Fermi level.

Generalized Hydrodynamics (GHD) and the Generalized Gibbs Ensemble (GGE) provide complementary theoretical approaches to describe the time evolution of isolated, interacting quantum systems following a quench or perturbation. GHD is a macroscopic approach, formulating equations for the evolution of local conserved quantities and their spatial gradients, effectively treating the system as a continuous fluid; it predicts the formation of shock waves and the separation of different regions with distinct densities. The GGE, conversely, is a microscopic statistical ensemble defined by the expectation values of conserved quantities with respect to the initial state; it provides a stationary state description of the post-quench dynamics. By comparing predictions from GHD and GGE with experimental results – particularly in cold atom systems where many-body interactions are highly controllable – researchers can validate these theoretical frameworks and gain a deeper understanding of non-equilibrium quantum dynamics, including transport properties and relaxation processes.

Beyond Conventional Signatures: Observing the Quantum Fingerprint

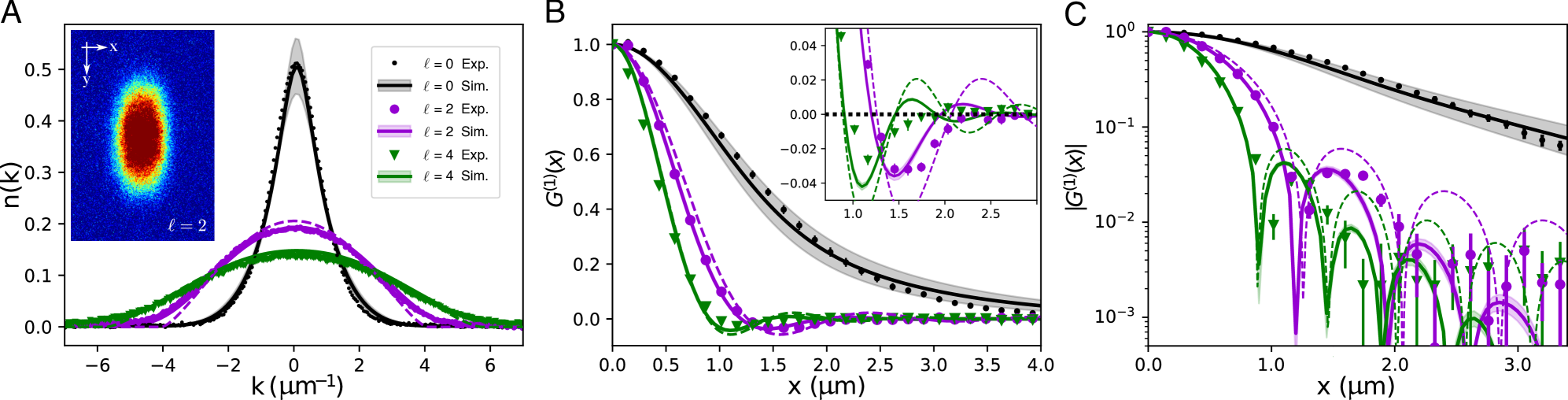
A crucial aspect of characterizing this quantum gas relies on Time-of-Flight (TOF) expansion, a technique where the ultracold atoms are released from their confining potential and allowed to spread. By observing the resulting distribution of atoms over time, researchers can precisely map the momentum distribution of the gas. This is not merely a measurement of individual particle speeds; it reveals intricate correlations between the atoms. Specifically, the observed broadening and shaping of the momentum distribution provides direct evidence of how the atoms are interacting and influencing each other’s motion, confirming the presence of collective quantum behavior. The precision of TOF expansion allows for the detection of subtle features in the momentum distribution, unveiling details about the underlying quantum state and confirming the existence of unique quantum phenomena within the gas.

The observation of Friedel oscillations within the system’s correlation functions provides compelling evidence for the existence of fractional Fermi seas – a departure from the typical, fully occupied or empty energy levels seen in conventional Fermi gases. These oscillations, a decaying pattern of density modulations, arise due to the long-range interactions between particles and are directly linked to the unique quantum statistics governing their behavior. Unlike bosons or fermions with integer occupancy, the fractional Fermi sea exhibits a distribution where particles partially occupy energy levels, leading to these distinct oscillatory patterns in the correlation functions. The presence and characteristics of these oscillations thus serve as a signature of this exotic state of matter, confirming the system’s departure from standard quantum statistical descriptions and supporting the theoretical predictions surrounding fractionalization phenomena in strongly interacting systems.

The observed sTG state proved remarkably stable, persisting for a full 5.4 seconds before significant decay occurred. This extended lifetime is crucial, as it allows for detailed spectroscopic measurements and confirms the robustness of the created quantum state against external perturbations. Such longevity distinguishes this system from many other ultracold gas experiments, where fleeting phenomena often limit the precision of investigations; the sustained coherence enables researchers to confidently map the underlying quantum correlations and verify theoretical predictions about the gas’s exotic properties. The ability to maintain this state for several seconds represents a significant advancement in the field, opening avenues for exploring more complex many-body physics and testing the limits of quantum statistics.

Detailed analysis of the gas’s momentum distribution revealed a broadening of the velocity spread, quantified by the Full Width at Half Maximum (FWHM). Measurements indicated a FWHM of 1.72 μm⁻¹ for the ℓ=0 angular momentum state, suggesting a relatively narrow momentum spread for particles with zero angular momentum. This value increased significantly to 5.19 μm⁻¹ for the ℓ=2 state, and further to 6.69 μm⁻¹ for ℓ=4, demonstrating a clear correlation between angular momentum and momentum uncertainty – higher angular momentum states exhibit a broader distribution of momenta. These values provide crucial insight into the kinetic energy and spatial confinement of the atoms within the system, and serve as a quantitative measure of the observed quantum statistics.

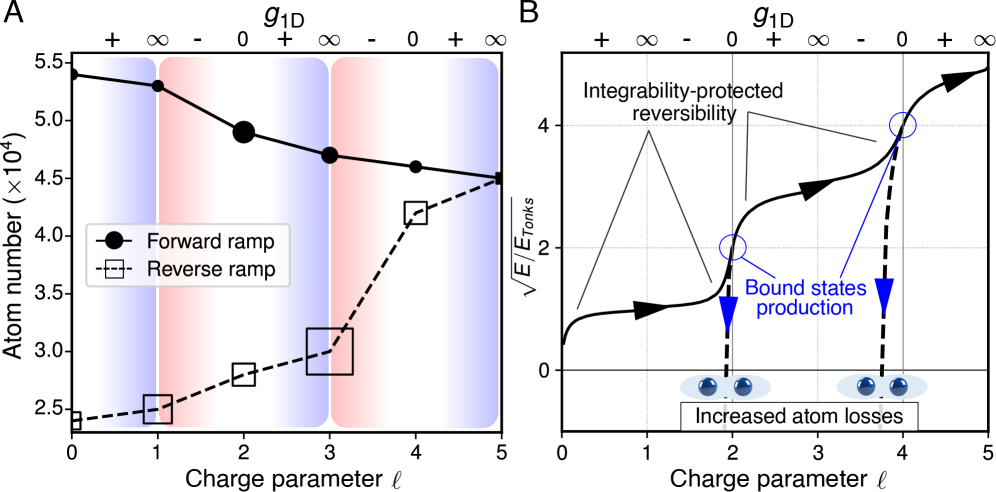
Experimental manipulation of the ultracold gas revealed a distinct asymmetry in atom loss during interaction cycles, indicating a fundamental irreversibility within the system. Specifically, a forward ramping of interaction parameters resulted in the loss of 20% of the atoms comprising the gas, whereas reversing the ramping process led to a significantly greater loss of 45%. This disparity suggests that the system does not simply return to its initial state after a cycle of interaction, and the reversal process introduces additional mechanisms contributing to atom loss – effectively demonstrating that the observed interactions are not time-reversible and hinting at the dissipation of energy within the sTG state.

The pursuit of understanding these fractional Fermi seas feels remarkably akin to chasing shadows. This work, demonstrating the realization of these seas through interaction-ramping cycles and the observation of Friedel oscillations, suggests a reality far stranger than simple exclusion statistics allowed for. It’s a delicate dance with quantum mechanics, where the theoretical elegance of integrable systems meets the messy, beautiful complexity of experiment. As Isaac Newton once noted, “I do not know what I may seem to the world, but to myself I seem to be a boy playing on the seashore.” The researchers, like that boy, are collecting the smooth stones of data, knowing full well the ocean of the unknown will always reclaim its due. Physics is the art of guessing under cosmic pressure, and this study reveals just how much pressure exists.

What Lies Beyond the Horizon?

The realization of fractional Fermi seas, as demonstrated through interaction-ramping cycles in a one-dimensional Bose gas, presents a curious juncture. The observation of Friedel oscillations offers a tangible foothold, yet serves as a stark reminder of the limits of any attempt to fully map a quantum many-body system. Any theoretical framework, no matter how elegant, ultimately rests on approximations-a simplification of reality that may, and likely will, break down under more extreme conditions. The very notion of a ‘Fermi sea’ feels almost quaint when confronted with the inherent non-equilibrium nature of these systems.

Future investigations must address the stability of these fractional states against perturbations, moving beyond the idealized conditions of current experiments. A critical challenge lies in extending these studies to spatially inhomogeneous systems-a more realistic depiction of physical reality. The relationship between these fractional Fermi seas and the broader landscape of generalized hydrodynamics remains largely unexplored, representing a significant avenue for future research. The persistence of integrability, or its eventual breakdown, under increasingly complex interactions, will be a defining question.

Ultimately, the pursuit of understanding these exotic states serves not merely to populate the theoretical landscape, but to illuminate the inherent fragility of knowledge itself. Each observation, each refinement of theory, brings into sharper focus the vastness of what remains unknown-a humbling prospect for any aspiring architect of reality.

Original article: https://arxiv.org/pdf/2602.17657.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/

See also:

2026-02-20 13:11