Why Cause Must Follow Effect

by

Author: Denis Avetisyan

A new analysis reveals a fundamental principle governing causal relationships in complex systems, suggesting that entropy consistently increases from cause to effect.

The study demonstrates a robust retro-causal regularity, wherein nearly all physical states identified as causes demonstrably originated, within a defined timeframe, from the corresponding states representing their effects, suggesting a fundamental temporal relationship beyond simple sequentiality.
The study demonstrates a robust retro-causal regularity, wherein nearly all physical states identified as causes demonstrably originated, within a defined timeframe, from the corresponding states representing their effects, suggesting a fundamental temporal relationship beyond simple sequentiality.

This paper demonstrates a causal second law for robust regularities in the special sciences under assumptions of state-supervenience and measure-preservation, with implications for understanding time asymmetry.

The seeming ubiquity of the second law of thermodynamics raises questions about its scope beyond physics, particularly concerning causal regularities in special sciences. This paper, ‘The Causal Second Law’, argues that under reasonable assumptions-including state-supervenience and measure-preservation-a parallel causal second law holds: causal entropy cannot decrease from cause to effect within these domains. Establishing this principle not only clarifies the relationship between special sciences and physics but also offers a novel perspective on time asymmetry and the nature of causal explanation. Could this framework ultimately demonstrate that the arrow of time is not solely a thermodynamic phenomenon, but a more fundamental feature of causality itself?

The Illusion of Static Causation

Conventional analyses of causation frequently treat events as isolated instances, examining a moment in time without considering the preceding or subsequent states of a system. This static approach overlooks the fundamental reality that physical processes are rarely, if ever, instantaneous; instead, they unfold dynamically over time, with effects becoming new causes in an ongoing chain of interactions. A system’s current state isn’t simply the result of prior causes, but actively shapes future possibilities, rendering a single snapshot insufficient to fully grasp the causal web. Consequently, traditional methods often fail to identify crucial feedback loops, emergent behaviors, and the subtle interplay of forces that define complex systems – from weather patterns to biological organisms – ultimately limiting their predictive power and explanatory depth.

Conventional analyses of cause and effect often falter when applied to systems that change over time, because they treat causation as a singular event rather than a process unfolding across a history. A complete understanding requires acknowledging that an effect at one moment can become a contributing cause at a later one, creating feedback loops and complex dependencies. This is particularly evident in biological systems, where developmental pathways and evolutionary adaptations demonstrate how prior states fundamentally shape future outcomes. Simply identifying a present cause for a present effect overlooks the crucial role of past influences and the accumulated changes that define a system’s current state; therefore, a static view provides an incomplete, and potentially misleading, picture of causal relationships.

The fundamental asymmetry of time presents a significant challenge to defining causation, demanding a framework that acknowledges the inherent directionality of natural processes. Many physical laws appear time-reversible at a microscopic level, yet macroscopic events consistently unfold in a single direction – from past to future. A comprehensive theory of causation, therefore, cannot simply identify a correlation between events; it must explain why a cause precedes its effect and why reversing that temporal order typically yields an unintelligible or impossible scenario. This necessitates incorporating concepts like entropy and the second law of thermodynamics, which dictate an overall increase in disorder over time, providing an ‘arrow of time’ that aligns with our perception of causality. Successfully accounting for this irreversibility is crucial for distinguishing genuine causal relationships from mere statistical correlations and for building predictive models that accurately reflect the behavior of complex systems.

A robust causal regularity, observable as a connection between sets of physical states over time, reveals how a dynamical system evolves from one physical state to another.
A robust causal regularity, observable as a connection between sets of physical states over time, reveals how a dynamical system evolves from one physical state to another.

Modeling Causation as Dynamic Evolution

A Dynamical Systems Approach to causation posits that causal relationships are not static connections, but rather emerge from the time-dependent evolution of physical systems. This framework models systems as existing in a state that changes continuously according to deterministic or stochastic rules, effectively viewing causation as a process of state transition. Rather than identifying causes as discrete events, this approach focuses on the underlying physical laws and initial conditions that govern how a system’s state evolves over time, with any observed causal relationship being a manifestation of these underlying dynamics. Consequently, understanding causation requires tracking the system’s trajectory through its state space and identifying how changes in one variable predictably alter the future state of the system, thereby defining a causal influence.

State supervenience is a foundational principle for connecting abstract causal relationships, as defined in special sciences like psychology or economics, to the underlying physical reality. This principle asserts that any difference at a higher-level of description – for example, a change in a belief or a market fluctuation – necessarily corresponds to a difference in the physical state of the system. Without state supervenience, causal claims made at the special science level would lack a concrete basis in physical laws and mechanisms; a change in a higher-level property must be realized by a change in some physical property, even if that property is complex and difficult to identify. This correspondence is crucial for grounding causal explanations in the physical world and allows for the possibility of reducing or explaining special science phenomena in terms of physical processes.

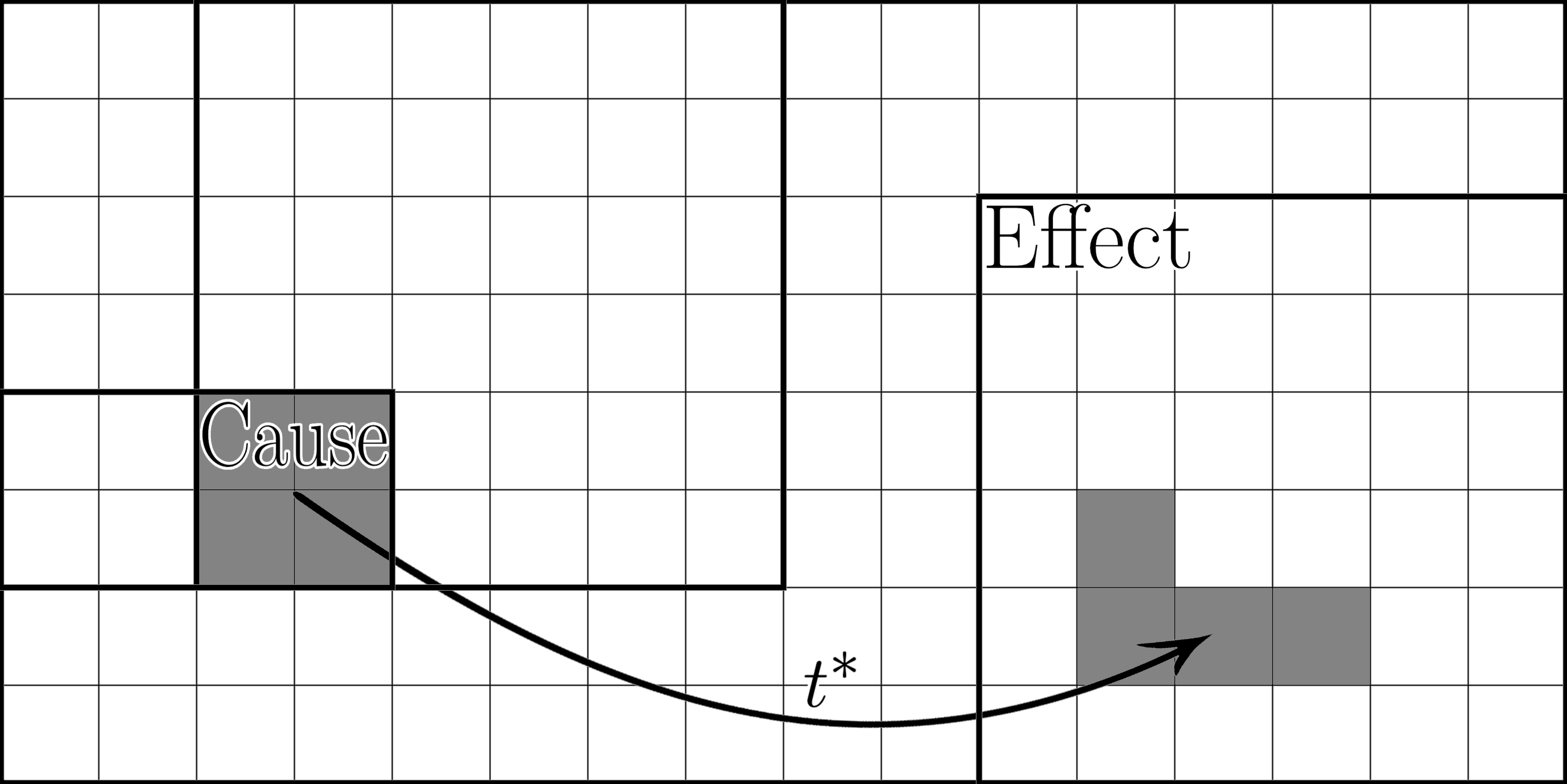
Causation, within a dynamical systems framework, is defined by state transitions occurring within a system’s PhaseSpace. PhaseSpace represents the complete set of possible states for a given system, where each point corresponds to a unique combination of variables describing the system’s condition. A causal relationship is therefore understood not as a static connection, but as the deterministic or probabilistic evolution of the system from an initial state to a subsequent state within this space. Specifically, if state x_t at time t leads to state x_{t+1} at time t+1 according to the system’s governing equations, this constitutes a causal link. Analyzing trajectories within PhaseSpace allows for the identification of attractors, bifurcations, and other dynamical features which characterize the system’s behavior and define the range of possible causal outcomes.

Special science states of affairs, including situations, causal factors, and effects, are represented by an Euler diagram and correspond to underlying physical states through state-supervenience.
Special science states of affairs, including situations, causal factors, and effects, are represented by an Euler diagram and correspond to underlying physical states through state-supervenience.

Quantifying Causal Direction and Stability

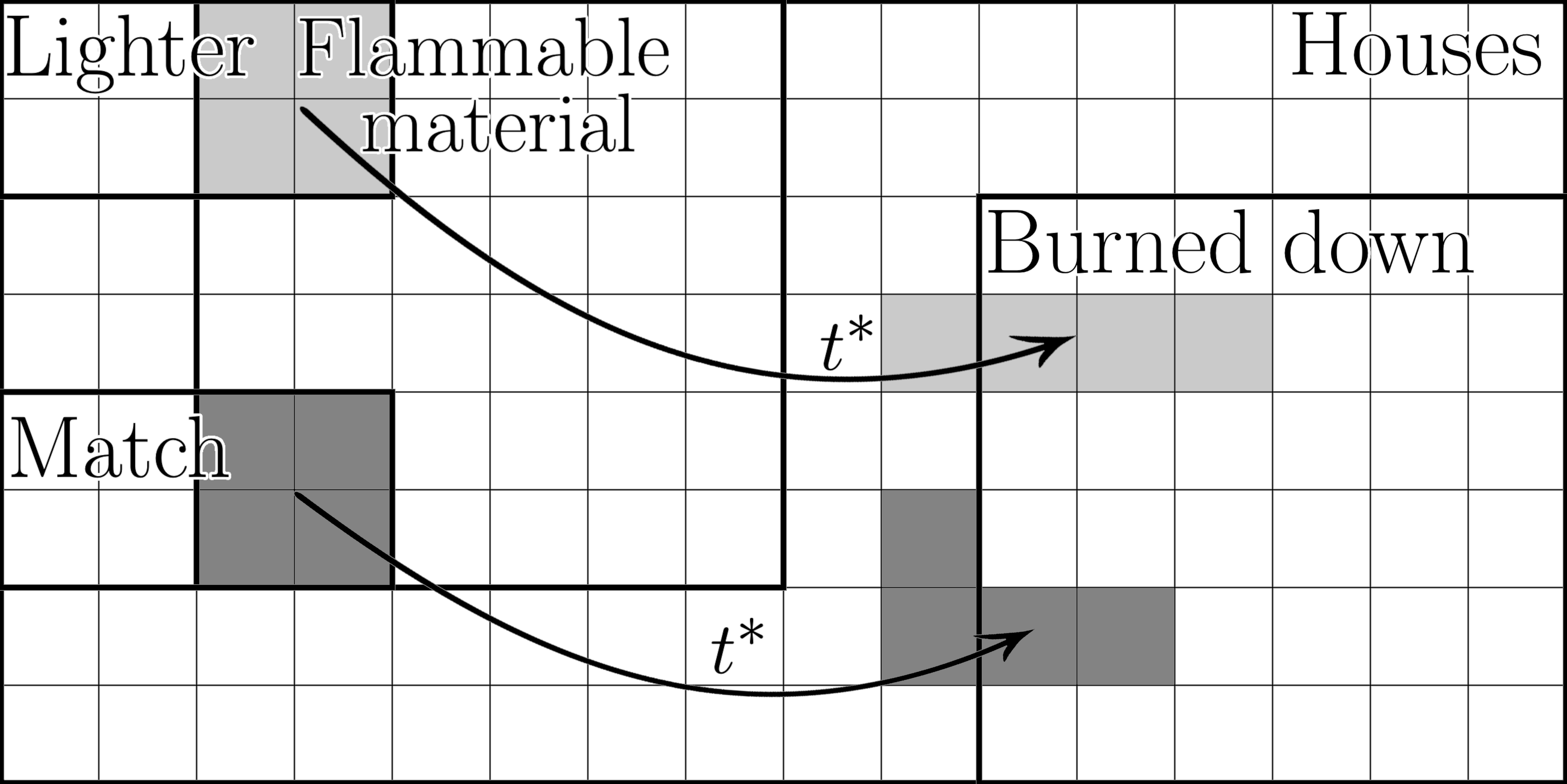
HistorySupervenience is utilized to determine the directional component of causation by analyzing state evolution through TransitionRelativeFrequency. This metric quantifies the probability of transitioning from one state to another; a value of 1 indicates a deterministic relationship where the current state entirely determines the subsequent state. This establishes a TransitionRelativeFrequency of 1 as the threshold for defining a robust causal regularity – meaning, given an initial condition, the system’s future evolution is predictably determined by that condition. Essentially, HistorySupervenience identifies causal direction by verifying that effects consistently follow their causes over time, and a TransitionRelativeFrequency of 1 signifies a consistently observed, robust causal link.

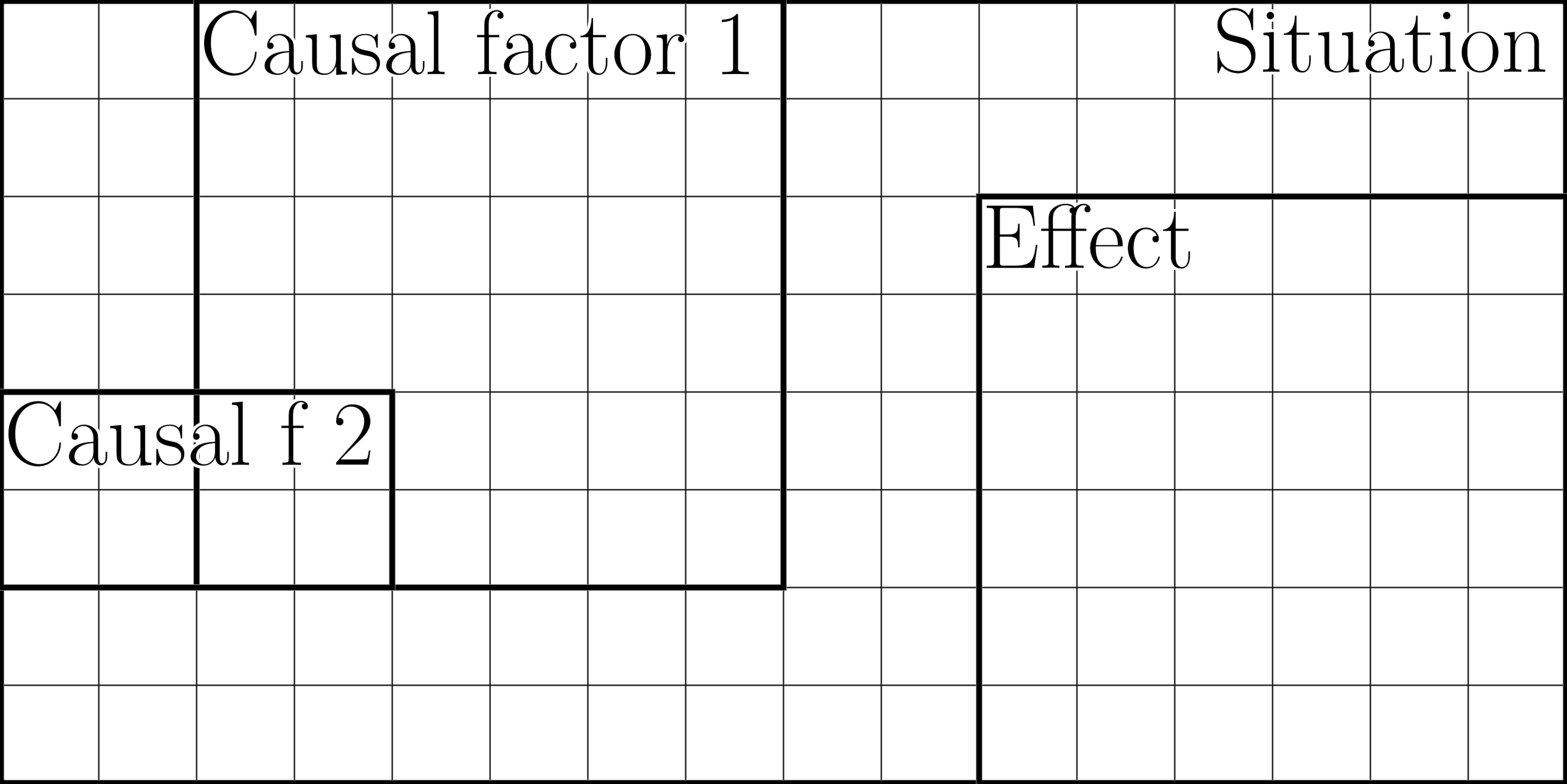
CausalEntropy quantifies the multiplicity of physical realizations for a given cause or effect, effectively measuring the ‘volume’ of possible causal pathways. This metric is fundamentally a non-decreasing quantity, a property derived from the principles of measure-preserving dynamics and state-supervenience. Measure-preserving dynamics ensures that the total ‘volume’ of states remains constant over time, while state-supervenience dictates that higher-level states are fully determined by lower-level states; together, these principles guarantee that causal entropy can only remain stable or increase, reflecting a consistent expansion of possible causal instantiations rather than a contraction. \Delta S_c \geq 0 , where S_c represents CausalEntropy.

RobustCausalRegularity denotes a condition where predictable evolution characterizes nearly all physical states within a system. This regularity is fundamentally supported by the CausalSecondLaw, which posits that causal entropy-a quantification of possible causal pathways-never decreases over time. Specifically, consistent application of this law ensures that as a system evolves, the ‘volume’ of instantiations of cause-and-effect relationships either remains constant or increases, thereby reinforcing the predictability of state transitions and solidifying the observed regularity. The principle of non-decreasing causal entropy is established through measure-preserving dynamics and state-supervenience, providing a mathematical foundation for this observed robustness.

Causal regularities in special sciences can be demonstrated using only transition frequencies, independent of the underlying physical states of cause and effect.
Causal regularities in special sciences can be demonstrated using only transition frequencies, independent of the underlying physical states of cause and effect.

Beyond Conventional Causation: Exploring the Boundaries of Time and Probability

The study of causality isn’t limited to the conventional flow from past to future; this framework permits the investigation of retrocausality – where future events influence the past – without introducing paradoxes or breaking established physics. By grounding causal relationships within the mathematics of dynamical systems, effects preceding causes become a permissible, albeit unusual, characteristic of certain system behaviors. This isn’t a claim that effects always precede causes, but rather that the model doesn’t inherently rule it out, offering a space to explore scenarios where future states can, under specific conditions, exert influence on prior states. The framework achieves this by focusing on the relationships between states, rather than imposing a strict temporal order, allowing for a more nuanced understanding of how information and influence can propagate within a system, even seemingly against the arrow of time.

The conventional understanding of causation often implies a complete predictability – that a cause will always result in a specific effect. However, PortionalCausalRegularity proposes a more nuanced reality, acknowledging that many causal relationships are fundamentally probabilistic. This framework suggests that a cause doesn’t guarantee an effect in every instance, but rather influences a portion of possible states, transitioning them predictably. Crucially, the existence of any causal link, even a partial one, is quantified by an ‘efficacy’ value α. A value of α greater than zero indicates that a cause has some, albeit potentially limited, influence on the system’s evolution; a value of zero implies no causal relationship whatsoever. This approach moves beyond deterministic views, recognizing that even seemingly reliable connections may operate with inherent probabilities, and offering a quantifiable measure of causal strength beyond simple presence or absence.

The consistency of any dynamical system – and therefore the validity of exploring non-standard causal relationships – fundamentally relies on the principle of Measure Preservation. This principle dictates that the total ‘volume’ of probability within the system remains constant over time, preventing the emergence of paradoxical scenarios where probabilities are created or destroyed. Without Measure Preservation, the system’s evolution would become unphysical, potentially allowing for effects without causes or violating the laws of conservation. By explicitly incorporating this established physical constraint, the framework ensures that even while investigating phenomena like retrocausality or partial determinism, the underlying mathematical structure remains grounded in established principles, avoiding logical inconsistencies and maintaining a connection to observable reality. This adherence to Measure Preservation provides a robust foundation for exploring the boundaries of causation itself.

Proportional causal regularities are demonstrated with efficacy of <span class="katex-eq" data-katex-display="false">\\frac{3}{4}</span> for a lit lighter and <span class="katex-eq" data-katex-display="false">\\frac{1}{2}</span> for a burning match.
Proportional causal regularities are demonstrated with efficacy of \\frac{3}{4} for a lit lighter and \\frac{1}{2} for a burning match.

The pursuit of a causal second law, as detailed in the paper, necessitates a careful consideration of how regularities within special sciences relate to underlying physical laws. The analysis hinges on assumptions regarding state-supervenience and measure-preservation – conditions that, if unmet, could reveal the fragility of seemingly robust causal claims. This echoes Richard Feynman’s sentiment: “The first principle is that you must not fool yourself – and you are the easiest person to fool.” Just as self-deception obscures truth, failing to rigorously examine the foundations of causal inference – to test how sensitive conclusions are to deviations from ideal conditions – risks building explanatory structures on unstable ground. The paper’s emphasis on identifying conditions under which entropy cannot decrease from cause to effect exemplifies this commitment to honest evaluation, a process of continual refinement through the identification of potential failures.

Where Do We Go From Here?

The demonstration of a causal second law, even within the constrained domain of robust causal regularities, doesn’t resolve the deeper issue of time’s arrow. It merely pushes the question downward, demanding a rigorous accounting of what constitutes ‘measure-preservation’ at each level of scientific description. The assumption of state-supervenience, while common, remains a point of contention – particularly when considering systems exhibiting emergent behavior. If the supervenience base isn’t fully determinate, the causal second law’s applicability becomes probabilistic, not absolute.

Future work must address these limitations. Quantifying the degree of supervenience-or demonstrating its failure-in complex systems is paramount. Furthermore, extending this framework beyond idealized dynamical systems-to encompass stochastic processes and genuinely open systems-will prove challenging. The paper’s reliance on measure-preservation invites investigation into alternative formulations of causality that might circumvent this requirement, perhaps at the cost of predictive power.

Ultimately, the true test isn’t theoretical consistency, but empirical falsification. If reproducible violations of this proposed causal second law are identified-even rare, localized ones-the framework will require substantial revision. Until then, it remains a useful, if provisional, step towards understanding why effects consistently follow causes, and not the other way around.

Original article: https://arxiv.org/pdf/2602.17150.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/

See also:

2026-02-21 00:58