Gravity’s Chaotic Echo: Fermions and the Limits of Prediction

Author: Denis Avetisyan

New research reveals a surprising link between three-dimensional gravity, fermionic particles, and the hallmarks of quantum chaos in their two-dimensional counterparts.

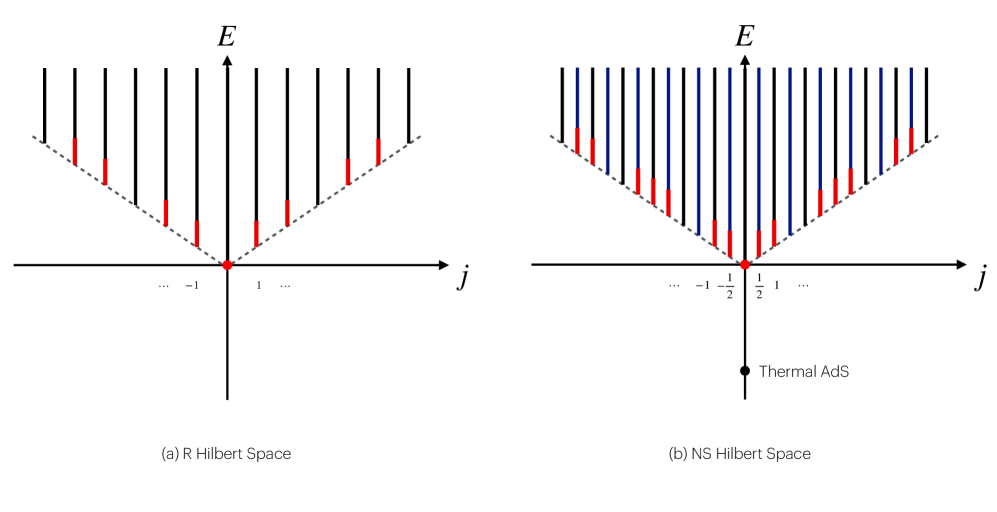
The study of fermionic gravity, as demonstrated through gravitational path integrals on a solid torus, reveals a spectrum of states-including bosonic and fermionic black holes denoted by energy thresholds <span class="katex-eq" data-katex-display="false">E \geq |j|</span> where <span class="katex-eq" data-katex-display="false">j \in \mathbb{Z}</span>-and further distinguishes these states through the presence of both positive and negative energy contributions, each characterized by an edge proportional to <span class="katex-eq" data-katex-display="false">1/\sqrt{E-|j|}</span>. — The study of fermionic gravity, as demonstrated through gravitational path integrals on a solid torus, reveals a spectrum of states-including bosonic and fermionic black holes denoted by energy thresholds $E \geq |j|$ where $j \in \mathbb{Z}$ -and further distinguishes these states through the presence of both positive and negative energy contributions, each characterized by an edge proportional to $1/\sqrt{E-|j|}$ .

This study demonstrates that the spectral form factor of fermionic 3D gravity exhibits behavior consistent with chaotic systems, providing insights into holographic duality and connections to random matrix theory.

The holographic principle suggests a deep connection between gravity and quantum field theory, yet incorporating fermions-fundamental particles with intrinsic angular momentum-into these dualities remains a significant challenge. This research, presented in ‘3D Gravity and Chaos in CFTs with Fermions’, investigates a novel theory of fermionic 3D gravity and its correspondence to a 2D conformal field theory, revealing a surprising link to quantum chaos. Specifically, we demonstrate that the spectral form factor derived from gravity calculations aligns with the characteristics of chaotic systems, even in the absence of bulk fermionic matter, and is consistent with anomalies predicted by fermionic CFT classifications. Could this framework offer new insights into the emergence of spacetime and the nature of quantum gravity itself?

Symmetry’s Delicate Dance: Anomalies and the Fabric of Spacetime

The pursuit of a consistent theory of quantum gravity demands meticulous attention to anomalies-subtle breakdowns in the expected symmetries of physical systems. These deviations aren’t merely mathematical curiosities; they represent fundamental obstructions to constructing a self-consistent theory where gravity and quantum mechanics coexist. Anomaly cancellation-the requirement that these symmetry violations precisely balance out-becomes a stringent constraint on the allowed mathematical structures and particle content of any viable quantum gravity model. Failing to address anomalies can lead to inconsistencies like non-gauge invariance or the appearance of unphysical particles, effectively rendering a theory untenable. The very fabric of spacetime, therefore, is subject to these delicate balancing acts, highlighting the profound connection between symmetry, consistency, and the quantum nature of gravity.

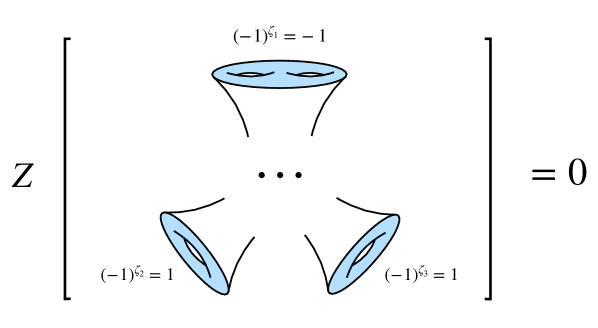
The emergence of quantum anomalies isn’t merely a mathematical curiosity, but a consequence of the underlying topology of spacetime itself. Cobordism, a branch of topology concerned with manifolds differing only by the addition of ‘handles’ or ‘caps’, provides a powerful framework for classifying these anomalies. Essentially, anomalies arise when a physical theory, perfectly consistent on a given manifold, becomes inconsistent when the manifold undergoes a topologically allowed deformation. This isn’t a failure of the theory, but a reflection of the manifold’s inherent structure – a specific cobordism class dictates the permissible symmetries and, crucially, the types of anomalies that can appear. By understanding how manifolds relate through cobordisms, physicists gain insight into the origin of these anomalies and can construct consistent quantum theories that respect the fundamental geometry of spacetime; a manifold’s topological invariants directly constrain the allowed symmetry configurations, thereby resolving potential inconsistencies and offering a pathway toward a complete theory of quantum gravity.

The fundamental nature of fermions-particles with half-integer spin-introduces a critical constraint on the symmetries permitted in a quantum gravity theory. Unlike bosons, fermions cannot occupy the same quantum state, and this antisymmetry requirement profoundly impacts how they interact with spacetime geometry. Specifically, consistent descriptions necessitate careful consideration of spin structures – a way of defining the quantum mechanical spin of particles on a given manifold. These structures dictate allowable boundary conditions, effectively shaping the topological properties of spacetime and determining which symmetry configurations are physically viable. A mismatch between the spin structure and the underlying geometry results in anomalies – breakdowns of classical symmetries at the quantum level – potentially leading to inconsistencies in the theory. Therefore, understanding and classifying these spin structures is crucial for constructing a self-consistent framework for quantum gravity, ensuring that the fermionic content of the universe does not destabilize the very fabric of spacetime.

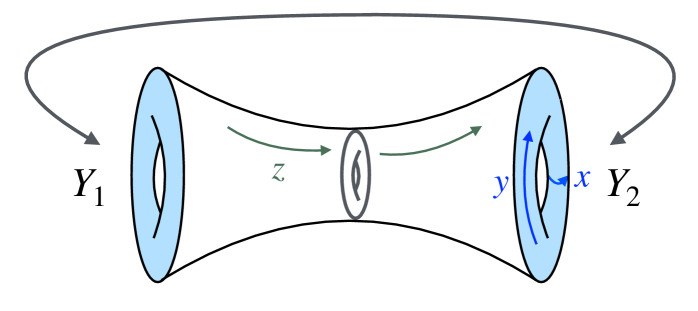
Cobordism invariance on a manifold with boundary is computed on a compact manifold by patching together two 2-tori with differing spin structures connected by a codimension-one defect, resulting in a 3D mapping torus.

Holographic Duality: A Potential Path Through the Chaos

The investigation of three-dimensional gravity incorporating fermionic fields provides a specific model for examining the holographic principle, also known as the AdS/CFT correspondence. This approach establishes a duality between a gravitational theory in three dimensions and a two-dimensional Conformal Field Theory (CFT) residing on the boundary of the gravitational space. The inclusion of fermions complicates the analysis, requiring careful consideration of their quantum properties and interactions within the gravitational background. This particular 3D gravity/2D CFT pairing offers a tractable system for studying the general principles of holographic duality, allowing for calculations and predictions that can be compared between the gravitational and field theory descriptions, potentially resolving long-standing problems in quantum gravity and strongly coupled systems.

Modular invariance, a crucial consistency condition in the context of 3D gravity and its holographic connection to 2D Conformal Field Theory (CFT), dictates that the partition function $Z$ remains unchanged under specific transformations known as modular transformations. These transformations relate different ways of summing over gravitational states. The requirement of modular invariance constrains the allowed spectrum of states and couplings within the gravitational theory. Critically, the specific choice of spin structure-which defines how fermions are treated under parity transformations-directly impacts the modular properties of the partition function and, therefore, the consistency of the gravitational calculation. Different spin structures lead to different modular transformation rules and necessitate corresponding adjustments to maintain a consistent holographic duality.

The holographic duality between three-dimensional gravity and two-dimensional Conformal Field Theory (CFT) provides a mathematical equivalence allowing problems traditionally addressed using gravitational theories to be reformulated and solved within the framework of CFT. This translation is achieved through a mapping of gravitational degrees of freedom to those of the CFT, enabling the calculation of quantities like correlation functions in the CFT that correspond to amplitudes in the gravitational theory. Consequently, strongly coupled gravitational systems-those intractable with conventional perturbative methods-can be analyzed through the weakly coupled CFT side, and vice versa, offering a non-perturbative approach to both gravitational physics and conformal field theories. This correspondence facilitates calculations of $\text{S}_{\text{CFT}}$ which are equivalent to calculating the gravitational partition function $Z_{\text{gravity}}$ .

The gravitational path integral vanishes when the sum of all boundary spin values is odd <span class="katex-eq" data-katex-display="false">\sum_{i}\zeta_{i}=1~\\text{mod}~2</span>, implying that a 3D spin surface cannot exist for non-zero spin values and applies to both tori and more complex surfaces. — The gravitational path integral vanishes when the sum of all boundary spin values is odd $\sum_{i}\zeta_{i}=1~\\text{mod}~2$ , implying that a 3D spin surface cannot exist for non-zero spin values and applies to both tori and more complex surfaces.

Randomness and Order: Probing Chaos with Spectral Statistics

The Spectral Form Factor (SFF), denoted as $S(t) = \sum_i e^{i \epsilon_i t}$ , quantifies the fluctuations of energy levels in a quantum system and is a central observable for diagnosing quantum chaos. In the context of the dual Conformal Field Theory (CFT), the SFF measures the sensitivity of the CFT to perturbations and provides information about the distribution of energy level spacings. Specifically, a linear increase in the SFF with time $t$ is characteristic of the spectral statistics predicted by Random Matrix Theory (RMT) for chaotic systems, while non-chaotic systems exhibit different behaviors like logarithmic growth or saturation. Therefore, deviations from RMT predictions in the SFF directly indicate a departure from chaotic behavior within the dual CFT, serving as a key diagnostic tool.

Random Matrix Theory (RMT) offers a statistical description of the energy levels observed in quantum systems exhibiting chaotic behavior. Specifically, RMT predicts universal fluctuations in spectral properties, independent of the microscopic details of the system. These predictions, derived from ensembles of random matrices – such as the Gaussian Orthogonal Ensemble (GOE) or Gaussian Symplectic Ensemble (GSE) – provide a quantifiable benchmark against which to compare the Spectral Form Factor (SFF). By examining the statistical properties of the SFF, and demonstrating its agreement with RMT predictions – specifically concerning the growth rate and late-time behavior – one can infer the presence and degree of quantum chaos in the system under investigation. The universality of RMT makes it a particularly valuable tool for analyzing complex systems where detailed knowledge of the Hamiltonian is unavailable.

The RMT2 framework establishes a quantitative connection between the Spectral Form Factor (SFF) and the modular completion of data generated from random matrix ensembles. This framework allows for the precise calculation of the SFF based on the statistical properties of random matrices, providing a benchmark against which to compare the behavior of the dual Conformal Field Theory (CFT). Specifically, the modular completion process relates the SFF to the behavior of the system under modular transformations, revealing information about the underlying chaotic dynamics. Agreement between the analytically calculated SFF derived from RMT2 and the numerically computed SFF of the dual CFT provides strong evidence supporting the claim that the CFT exhibits chaotic behavior, offering a concrete, quantifiable measure of this characteristic.

Higher-dimensional bulk topological quantum field theory effects can be investigated through twisted gluings, as demonstrated by the repulsion observed when gluing black hole double-cone boundaries after applying a transformation <span class="katex-eq" data-katex-display="false">\xi\xi</span> (potentially a large diffeomorphism, fermion parity, or <span class="katex-eq" data-katex-display="false">{\\sf RT}</span>) and the resulting modification to the black hole spectrum when gluing two black holes with the same twist. — Higher-dimensional bulk topological quantum field theory effects can be investigated through twisted gluings, as demonstrated by the repulsion observed when gluing black hole double-cone boundaries after applying a transformation $\xi\xi$ (potentially a large diffeomorphism, fermion parity, or ${\\sf RT}$ ) and the resulting modification to the black hole spectrum when gluing two black holes with the same twist.

A Delicate Balance: Fermion Parity and Gravitational Consistency

The foundational structure of a conformal field theory (CFT) incorporates a unitary ℤ2 symmetry, which mathematically represents fermion parity – the inherent property distinguishing fundamental particles like electrons and quarks. This symmetry isn’t merely a theoretical elegance; it actively constrains calculations within the corresponding gravitational theory. Specifically, any consistent calculation of gravitational interactions must respect this parity, meaning transformations that flip the ‘handedness’ of fermions cannot lead to inconsistencies. Violations of this constraint signal a breakdown in the theory’s self-consistency, potentially indicating the need for new physics or a revised understanding of gravity’s interplay with matter. Essentially, the ℤ2 symmetry acts as a powerful regulator, ensuring that gravitational calculations remain physically meaningful and avoid paradoxical results, highlighting a deep connection between particle physics and the fabric of spacetime itself.

The introduction of fermions into three-dimensional gravity isn’t without its challenges, primarily stemming from potential violations of fermion parity – a symmetry dictating how fermions transform under certain operations. When this symmetry breaks down, it results in anomalies – mathematical inconsistencies that threaten the self-consistency of the gravitational theory. These anomalies aren’t merely theoretical curiosities; they directly impact the allowed interactions and properties of the gravitational field, potentially leading to unphysical predictions like infinite probabilities or violations of fundamental conservation laws. Consequently, ensuring the preservation of fermion parity – or carefully accounting for its breakdown – becomes crucial for constructing a viable and consistent theory of gravity that incorporates matter described by fermionic fields, demanding a delicate balancing act between symmetry principles and the mathematical structure of the theory itself.

The pursuit of a consistent theory of gravity incorporating fermions reveals a surprisingly fragile interplay between fundamental symmetry and inevitable anomalies. Maintaining fermion parity-a core symmetry dictating particle-antiparticle correspondence-places strict limitations on gravitational calculations; any deviation results in anomalies that threaten the theory’s mathematical coherence. These anomalies aren’t merely technical glitches, but rather indicators of a deeper tension: the attempt to reconcile quantum mechanics with general relativity, especially when matter is involved, demands an exquisite balance. A slight misalignment – a violation of this delicate symmetry – can render the entire gravitational framework inconsistent, underscoring that seemingly abstract mathematical requirements reflect the very fabric of physical reality and the constraints on constructing viable models of the universe.

The <span class="katex-eq" data-katex-display="false">D-1</span>-dimensional boundary is characterized by its topology, metric, and spin structure <span class="katex-eq" data-katex-display="false">\mathfrak{s}</span>, and the gravitational path integral sums over all <span class="katex-eq" data-katex-display="false">D</span>-dimensional manifolds with compatible bulk spin structures. — The $D-1$ -dimensional boundary is characterized by its topology, metric, and spin structure $\mathfrak{s}$ , and the gravitational path integral sums over all $D$ -dimensional manifolds with compatible bulk spin structures.

Looking Ahead: Holography and the Future of Quantum Gravity

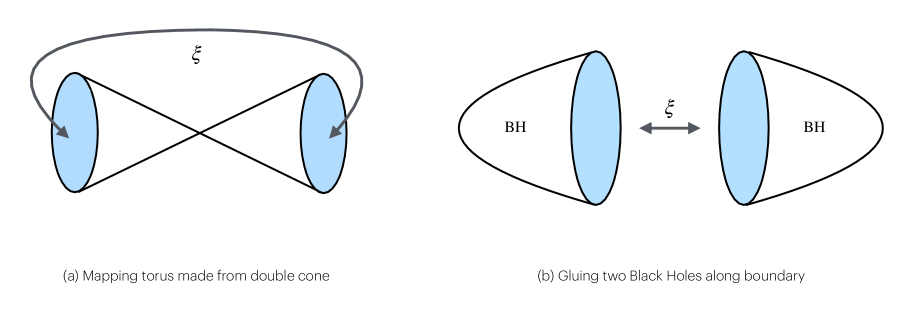
Holographic duality offers a surprising and potent framework for investigating quantum chaos within systems governed by gravity. This principle posits a correspondence between a gravitational theory in a given number of dimensions and a quantum field theory (CFT) residing in one fewer dimension – effectively projecting the gravitational system’s information onto a lower-dimensional ‘holographic screen’. This isn’t merely a mathematical trick; it transforms notoriously difficult calculations in quantum gravity into more manageable problems within the well-established toolkit of CFT. By studying the behavior of this dual CFT, researchers can indirectly probe the chaotic dynamics of the original gravitational system – including black holes – providing unprecedented insights into how information is scrambled and potentially recovered, even in the face of extreme gravitational forces. The power lies in leveraging the simplicity of the CFT to illuminate the complexities of gravity, offering a new lens through which to explore the fundamental nature of chaos in the universe.

The remarkable correspondence at the heart of holographic duality enables a translation of intensely complex gravitational problems into the framework of conformal field theory (CFT), a significantly more manageable theoretical landscape. This isn’t merely a mathematical trick; it’s a profound connection suggesting that all the information contained within a volume of space can be encoded on its boundary, much like a hologram. Consequently, researchers can leverage the well-developed tools of CFT – including perturbative techniques and numerical simulations – to analyze phenomena in strongly coupled gravitational systems, such as black holes, which are otherwise notoriously difficult to approach. This opens entirely new avenues for research, allowing for the investigation of quantum gravity effects and providing potential insights into the very fabric of spacetime, offering a path toward resolving long-standing paradoxes and furthering understanding of the universe’s fundamental laws.

The continued investigation of holographic duality holds the potential to fundamentally reshape understanding of gravity, quantum chaos, and the very fabric of reality. This theoretical framework suggests a deep connection between gravitational systems and quantum field theories, implying that the behavior of gravity can be described by principles governing quantum mechanics – and vice versa. By leveraging this correspondence, researchers aim to resolve long-standing paradoxes in physics, such as the information loss paradox in black holes, and to gain insight into the emergence of spacetime itself. The implications extend beyond theoretical physics, potentially influencing cosmology and our comprehension of the early universe, as well as providing novel approaches to studying complex quantum systems that defy traditional analytical methods. Ultimately, this pursuit promises to unveil previously hidden connections between seemingly disparate areas of physics, offering a more complete and unified picture of the universe’s fundamental laws.

The two-boundary torus wormhole is characterized by boundary moduli <span class="katex-eq" data-katex-display="false">$\\tau\\_{1},\\bar{\\tau}\\_{1}\$</span> and <span class="katex-eq" data-katex-display="false">$\\tau\\_{2},\\bar{\\tau}\\_{2}\$</span>, along with spin structures <span class="katex-eq" data-katex-display="false">$\\mathfrak{s}\\_{1}\$</span> and <span class="katex-eq" data-katex-display="false">$\\mathfrak{s}\\_{2}\$</span>. — The two-boundary torus wormhole is characterized by boundary moduli $\\tau\\_{1},\\bar{\\tau}\\_{1}\$ and $\\tau\\_{2},\\bar{\\tau}\\_{2}\$ , along with spin structures $\\mathfrak{s}\\_{1}\$ and $\\mathfrak{s}\\_{2}\$ .

The pursuit of elegant theoretical frameworks, even those attempting to bridge gravity with quantum field theory, invariably encounters the blunt reality of implementation. This research, connecting fermionic 3D gravity to the spectral form factor and holographic duality, feels less like a revolution and more like an exquisitely detailed specification. As Simone de Beauvoir observed, “One is not born, but rather becomes, a woman.” Similarly, these theoretical constructs don’t simply exist in a perfect state; they become manifest through the messy process of calculation and, ultimately, empirical scrutiny. The observed characteristics aligning with quantum chaos suggest a path forward, but it’s a path paved with approximations and the inevitable need for further refinement. If the code looks perfect, no one has deployed it yet.

The Road Ahead

The correspondence established between fermionic 3D gravity, spectral fluctuations, and the hallmarks of quantum chaos is, predictably, not a destination. It is merely a more elaborate scaffolding upon which future inconsistencies will accumulate. The observed agreement with random matrix theory offers a convenient benchmark, yet the precise mechanisms driving this behavior remain obscured – a familiar pattern. The elegance of holographic duality should not be mistaken for explanatory power; it’s a mapping, not a reduction.

Future work will undoubtedly focus on extending these calculations to more realistic, albeit messier, systems. The introduction of interactions, boundaries, or even a modicum of non-trivial topology will almost certainly reveal the limitations of current approaches. The spectral form factor, while a useful diagnostic, is ultimately a single observable. A comprehensive understanding will require probing a wider range of quantities, and bracing for further discrepancies.

It is worth remembering that ‘innovation’ in this field largely consists of repackaging established techniques with new mathematical flourishes. The goal isn’t deeper insight, but a slightly more resilient architecture before the inevitable entropy sets in. The question isn’t whether this framework will break down, but when. The field doesn’t need more sophisticated models-it needs fewer illusions.

Original article: https://arxiv.org/pdf/2602.17618.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/