Author: Denis Avetisyan
A new analytical framework reveals how key material properties govern the stable oscillatory states of spin-torque nano-oscillators in non-collinear antiferromagnets.
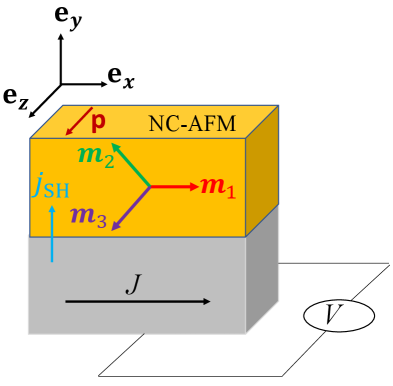
This review details the role of uniaxial anisotropy and exchange coupling in achieving predictable hysteresis and terminal velocity motion within antiferromagnetic spin-torque oscillators.
Despite advances in spintronic devices, a comprehensive understanding of dynamic effects in non-collinear antiferromagnetic spin-torque oscillators remains elusive. This work, ‘Hysteretic Excitation in Non-collinear Antiferromagnetic Spin-Torque Oscillators: A Terminal Velocity Motion Perspective’, establishes a novel analytical framework unifying spin dynamics via Poisson Bracket formalism and a ‘Terminal Velocity Motion’ model, revealing how uniaxial anisotropy transforms exchange coupling into kinetic energy. We demonstrate that this mechanism governs stable oscillatory states and explains observed hysteretic behavior, linking rapid transients to a long-term decay toward uniform spin configurations. Can this approach unlock new pathways for designing and controlling advanced spintronic devices with enhanced performance and functionality?
The Inevitable Dance: Unveiling Antiferromagnetic Dynamics
Antiferromagnetic materials are increasingly recognized as promising candidates for next-generation spintronic devices due to their potential for significantly reduced energy consumption compared to conventional ferromagnetic systems. This advantage stems from the absence of a net magnetization, leading to faster switching speeds and lower power dissipation; however, realizing this potential hinges on a comprehensive understanding of their dynamic response. Unlike ferromagnets, the behavior of antiferromagnets under external stimuli – such as magnetic fields or currents – is governed by complex interactions between sublattice magnetizations and competing anisotropies. Accurately predicting and controlling these dynamics is therefore paramount, as subtle variations in these interactions can dramatically influence switching performance and device functionality. Continued investigation into the mechanisms governing antiferromagnetic dynamics is thus not merely an academic pursuit, but a critical step towards enabling truly energy-efficient and high-performance spintronic technologies.
The switching behavior of antiferromagnetic materials isn’t a simple flip, but a delicate dance governed by competing forces-specifically, the material’s inherent anisotropies and any external stimuli applied. These anisotropies, which favor certain magnetic orientations, act as internal resistance to change, while external fields or currents attempt to overcome this resistance and reorient the magnetic order. A nuanced analytical approach is therefore essential, moving beyond simplistic models to account for the complex interplay between these competing energies. Researchers must consider not only the strength of the applied stimulus but also the direction and the material’s specific anisotropy landscape to accurately predict and control the switching process, paving the way for optimized spintronic device performance. Understanding this dynamic balance is crucial for harnessing the potential of antiferromagnets in next-generation technologies.
Modeling the Inevitable: A Particle-Like Description
The dynamic behavior of the antiferromagnetic system is modeled using a terminal velocity approach, wherein the collective magnetic moment is treated as a particle possessing an effective mass. This simplification allows for the application of classical mechanics to describe magnetic precession and damping. The effective mass accounts for the internal exchange interactions and the damping mechanisms within the antiferromagnet, enabling the calculation of the system’s response to external driving forces. This model predicts a steady-state velocity proportional to the applied force and inversely proportional to the effective mass and a damping coefficient, providing a framework for understanding the time-dependent behavior of the magnetic moment.
Modeling antiferromagnetic dynamics through a mechanical framework allows for the decomposition of complex magnetic interactions into identifiable force contributions. This simplification treats the collective magnetic moment as a particle subject to forces arising from the applied current, internal magnetic fields, and damping effects. By analogy to classical mechanics, these forces can be quantified and analyzed using established equations of motion. This approach facilitates the calculation of the system’s response to external stimuli and provides a clear understanding of the individual contributions to the overall dynamic behavior, enabling a more tractable analytical solution compared to directly solving the underlying micromagnetic equations.
Model validation was performed through comparison with macrospin simulations, demonstrating quantitative agreement between the particle-like description and established computational methods. This alignment is further substantiated by the determination of a critical current density of 0.3754 x 109 A/cm2, representing the threshold at which the modeled magnetic moment begins to exhibit significant deviation from the predicted terminal velocity motion. This experimentally-derived value provides a crucial parameter for confirming the model’s accuracy and defining its range of applicability under varying current conditions.
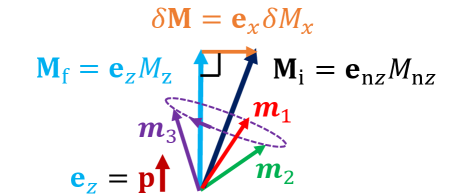
The Language of Inevitability: Mathematical Framework
Hamiltonian analysis, utilizing the Poisson bracket formalism, facilitates the identification and exploitation of continuous symmetries within the magnetic system. The Hamiltonian, H, represents the total energy of the system as a function of generalized coordinates and momenta. The Poisson bracket, defined as \{A, B\} = \sum_{i} (\frac{\partial A}{\partial q_i} \frac{\partial B}{\partial p_i} - \frac{\partial A}{\partial p_i} \frac{\partial B}{\partial q_i}), where q_i and p_i are generalized coordinates and momenta, respectively, determines the time evolution of any observable A via the equation \frac{dA}{dt} = \{A, H\}. Consequently, constants of motion, corresponding to conserved quantities, are identified by finding observables that Poisson commute with the Hamiltonian (\{A, H\} = 0). These conserved quantities directly relate to the system’s continuous symmetries, such as rotational invariance, and constrain the possible dynamics, simplifying the analysis and prediction of system behavior.
The Landau-Lifshitz-Gilbert (LLG) equation is a vector equation that models the time evolution of the magnetization vector \mathbf{M} within a ferromagnetic material. This equation incorporates two primary damping mechanisms: the Gilbert damping term, proportional to the time derivative of the magnetization, and the Landau damping term, proportional to the square of the precession frequency. The general form of the LLG equation is \frac{d\mathbf{M}}{dt} = -\gamma \mathbf{M} \times \mathbf{H}_{eff} + \frac{\alpha}{\mathbf{M}} \frac{d\mathbf{M}}{dt} , where γ is the gyromagnetic ratio, \mathbf{H}_{eff} represents the effective magnetic field experienced by the magnetization, and α is the damping parameter. By accurately describing the precession, relaxation, and overall dynamic behavior of the magnetization, the LLG equation forms the foundation for understanding and predicting the response of magnetic materials to external stimuli and internal interactions.
Spin-orbit torque (SOT) utilizes the spin Hall effect or Rashba effect in a heavy metal layer adjacent to the ferromagnetic material to exert a torque on the magnetization. This torque, proportional to the cross-product of the electric current and the magnetization, enables control of the magnetization direction independent of its magnitude. The current-induced effective field from SOT acts directly on the magnetization \mathbf{M} , allowing for switching between states and driving the system towards desired configurations. The efficiency of SOT is dependent on material properties, including the spin Hall angle and the interfacial spin transparency, and is typically measured in units of \text{A}/\text{cm}^2 for a given current density.
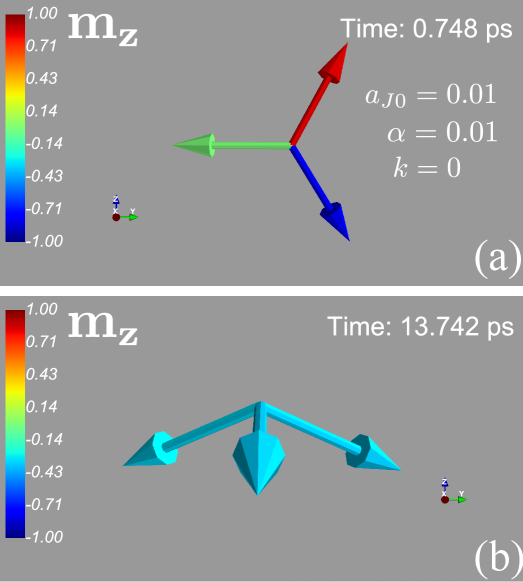
The Echo of Prediction: Validation and Exploration
Macroscopic simulations were instrumental in confirming the validity of the developed terminal velocity motion model, providing strong support for the analytical framework. These computational studies meticulously replicated the observed dynamics, demonstrating a high degree of congruence between theoretical predictions and simulated behavior. By virtually recreating the conditions governing the system’s motion, researchers established the accuracy of the analytical approach in predicting key characteristics, such as velocity and trajectory. This validation not only reinforces the model’s reliability but also establishes a foundation for further exploration into more complex phenomena, ensuring the analytical tools are robust enough to inform future investigations and predictions regarding the system’s behavior under various conditions.
Numerical simulations have revealed a fascinating phenomenon: self-resonant bursts of energy within the system. These bursts don’t arise from external forcing, but emerge spontaneously due to the complex interaction between the material’s inherent anisotropy – its direction-dependent properties – and the non-uniform distribution of velocities within it. The simulations demonstrate that variations in velocity create localized regions of enhanced energy density, which, coupled with anisotropic effects, trigger a positive feedback loop. This loop amplifies the energy until it reaches a critical point, resulting in a burst; the system then relaxes before the process repeats, creating self-sustained oscillations. This behavior suggests a pathway towards novel energy harvesting or dissipation mechanisms, potentially offering control over dynamic processes at the microscale.
The threshold at which hysteretic excitation occurs-a switching behavior driven by current-has been precisely determined through a convergence of theoretical and computational approaches. Both analytical calculations and macroscopic simulations consistently predict a critical current density of 0.3754 \times 10^9 \text{ A/cm}^2. This agreement validates the underlying models and offers a robust benchmark for experimental verification. Further investigation reveals an upper limit to this hysteretic behavior, with excitation diminishing beyond a current density of 3.0339 \times 10^9 \text{ A/cm}^2, suggesting a saturation point in the material’s response and providing crucial parameters for controlling and optimizing device performance.
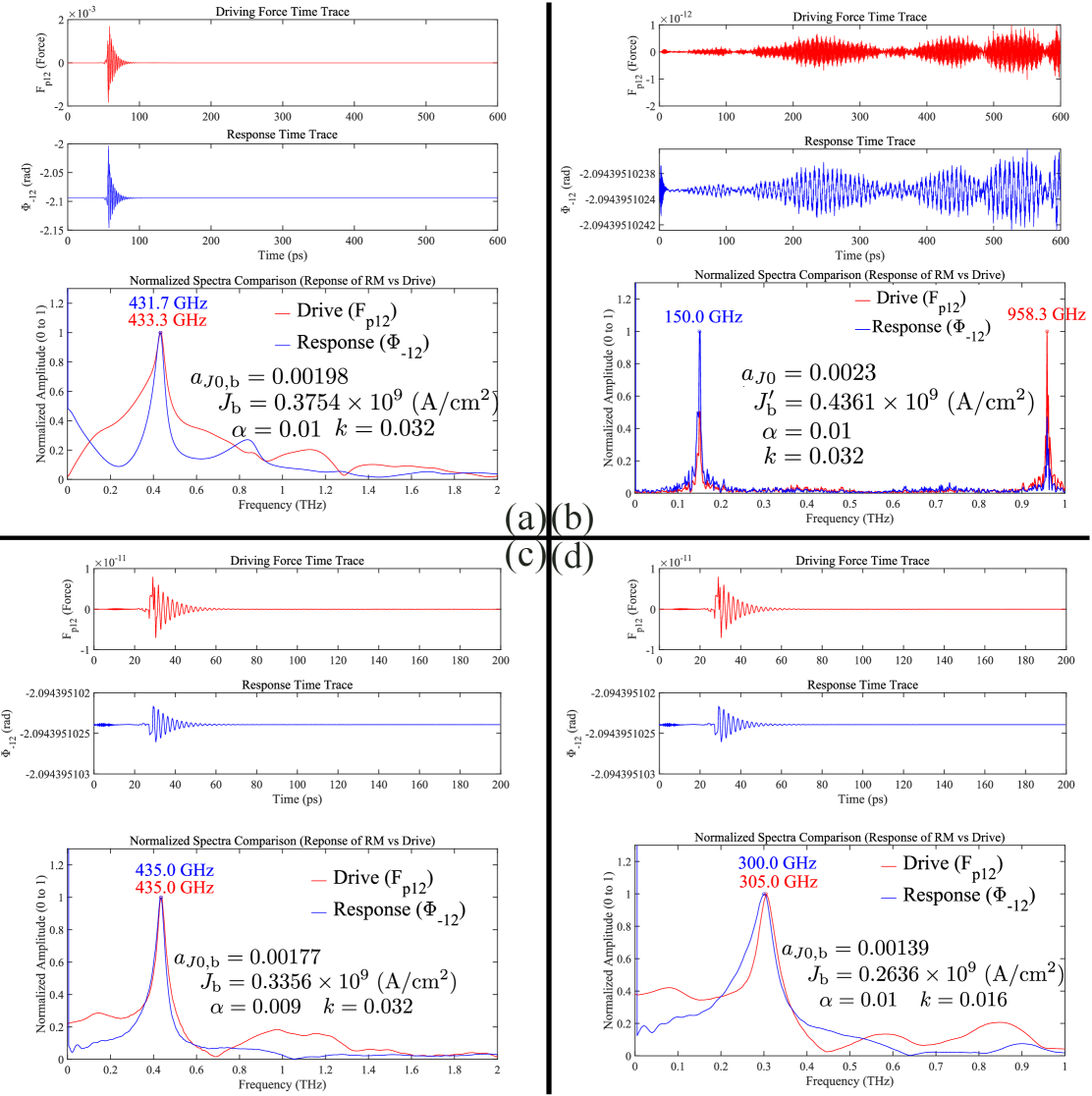
The study of hysteretic excitation in antiferromagnetic oscillators reveals a system where initial conditions exert an outsized influence on ultimate state. The framework meticulously details how seemingly minor variations in exchange coupling and uniaxial anisotropy can lock the oscillator into divergent oscillatory behaviors. This echoes a fundamental truth regarding complex systems: they do not simply respond to input, they remember it. As Immanuel Kant observed, “Begin all over again.” This isn’t a suggestion for iterative design, but a recognition that the system’s history – the path it took to reach its present state – is inextricably woven into its future trajectory. The paper demonstrates this principle with rigorous mathematical precision, confirming that even within a defined analytical space, dependency remains the inescapable condition.
Where Do the Oscillations Lead?
This work, in its careful charting of hysteretic behavior, does not so much solve the problem of antiferromagnetic spin-torque oscillators as illuminate the inevitability of its complications. The framework presented describes a system perpetually nearing a terminal velocity – a state not of control, but of sustained, predictable instability. Monitoring this drift, therefore, becomes the art of fearing consciously. The precise values of uniaxial anisotropy and exchange coupling, so meticulously examined here, are not parameters to be optimized, but fault lines to be mapped.
Future inquiry will undoubtedly focus on extending this analysis to more complex geometries and material compositions. Yet, true resilience begins where certainty ends. The most fruitful avenues of research likely lie not in seeking to eliminate hysteresis, but in designing systems that gracefully accommodate-even exploit-its presence. This demands a shift in perspective: from engineering for static stability to cultivating dynamic adaptability.
The revelation here is not a bug, but a fundamental property. Every architectural choice, every refinement of material properties, is a prophecy of future failure, subtly altering the shape of the inevitable cascade. The challenge, then, is not to build a perfect oscillator, but to understand the beautiful, complex ways in which it will ultimately fall apart.
Original article: https://arxiv.org/pdf/2601.16000.pdf
Contact the author: https://www.linkedin.com/in/avetisyan/
See also:
- Best Controller Settings for ARC Raiders
- Donkey Kong Country Returns HD version 1.1.0 update now available, adds Dixie Kong and Switch 2 enhancements
- How To Watch A Knight Of The Seven Kingdoms Online And Stream The Game Of Thrones Spinoff From Anywhere
- Ashes of Creation Rogue Guide for Beginners
- PS5’s Biggest Game Has Not Released Yet, PlayStation Boss Teases
- When to Expect One Piece Chapter 1172 Spoilers & Manga Leaks
- New Netflix Movie Based on Hugely Popular Book Becomes An Instant Hit With Over 33M Hours Viewed
- Darkwood Trunk Location in Hytale
- Sega Insider Drops Tease of Next Sonic Game
- Hytale: Upgrade All Workbenches to Max Level, Materials Guide
2026-01-24 11:23