Beyond Bell: Detecting Quantum Entanglement with Everyday Systems

by

Author: Denis Avetisyan

A new framework demonstrates that entanglement can be detected using rotationally covariant measurements, even with seemingly mundane systems like a glass of lemonade.

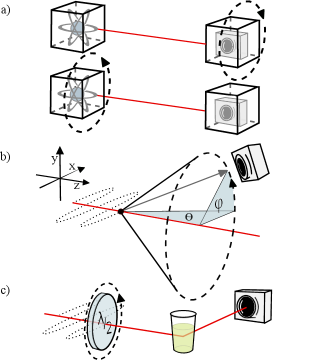
Rotational covariance emerges as a fundamental principle across diverse physical systems-from measurements invariant under $2\pi$ rotations, to the behavior of polarized photons in Compton scattering exhibiting covariance with respect to angle $\varphi$, and even extends to experimental setups like the manipulation of photon polarization via half-wave plates and subsequent detection-demonstrating that rotating the preparation or detection process yields equivalent descriptions.
Rotational covariance emerges as a fundamental principle across diverse physical systems-from measurements invariant under $2\pi$ rotations, to the behavior of polarized photons in Compton scattering exhibiting covariance with respect to angle $\varphi$, and even extends to experimental setups like the manipulation of photon polarization via half-wave plates and subsequent detection-demonstrating that rotating the preparation or detection process yields equivalent descriptions.

This review details a novel approach to entanglement detection using positive operator-valued measures (POVMs) and rotationally covariant observables, extending beyond traditional Bell inequality tests.

Detecting quantum entanglement remains a formidable challenge, particularly when constrained by realistic measurement devices. This work, ‘Entanglement Detection with Rotationally Covariant Measurements – From Compton Scattering to Lemonade’, introduces a framework for characterizing entanglement detection using measurements governed solely by rotational symmetry. We demonstrate that such measurements, exemplified by the Klein-Nishina formula for Compton scattering, are fully specified by a single parameter, and surprisingly, can be implemented with commonplace systems – even a glass of lemonade. Could this simplicity pave the way for accessible, practical quantum experiments and novel entanglement certification protocols?

Unveiling the Quantum Enigma: Beyond Classical Expectations

Classical physics operates on the principle of locality – that an object is only directly influenced by its immediate surroundings – and realism, the idea that objects have definite properties independent of observation. However, certain experimental results reveal correlations between particles that are far too strong to be explained by any theory adhering to both of these principles. These “local hidden variable” theories posit that particles carry pre-determined instructions dictating their behavior, but even the most sophisticated formulations fail to account for the observed strength of quantum correlations. This discrepancy isn’t simply a matter of incomplete knowledge; it fundamentally challenges the classical worldview, suggesting that either locality, realism, or both must be abandoned to accurately describe the behavior of the universe at a quantum level. The implications extend beyond foundational physics, hinting at the possibility of phenomena – like quantum entanglement – that defy classical intuition and unlock new technological possibilities.

Quantum entanglement, a phenomenon where two or more particles become linked and share the same fate no matter how far apart they are, is not merely a theoretical curiosity but the foundational principle underpinning the burgeoning field of quantum information science. This interconnectedness allows for correlations between particles that are demonstrably stronger than anything achievable through classical physics, defying intuitive notions of locality and realism. It is this non-classical correlation that enables protocols like quantum cryptography – promising unconditionally secure communication – and quantum teleportation, the transfer of quantum states, not matter, between locations. Furthermore, entanglement is a crucial resource for quantum computing, allowing quantum computers to perform certain calculations exponentially faster than their classical counterparts by leveraging the superposition and interference of quantum states. Without entanglement, many of the potential advantages of quantum technologies would remain unrealized, making it the central ingredient driving innovation in this revolutionary field.

Establishing genuine quantum entanglement isn’t simply observing correlation; it demands rigorously excluding all conceivable classical explanations for that correlation. This presents a formidable experimental hurdle, as any observed connection between particles could, in principle, arise from shared pre-existing properties – a ‘local hidden variable’ – or from subtle influences traversing the space between them. Researchers must therefore meticulously design experiments that close ‘loopholes’ – potential weaknesses in the setup that could allow for classical mimicry of quantum behavior. Bell’s theorem provides a mathematical framework for identifying correlations that are fundamentally incompatible with any local hidden variable theory, but realizing these predictions in a real-world experiment necessitates confronting technical challenges like detector inefficiencies and imperfect particle sources. The pursuit of loophole-free entanglement demonstrations isn’t merely academic; it’s crucial for validating the foundations of quantum technologies, from secure communication to powerful quantum computation, where entanglement serves as a vital resource.

Entanglement detection, simulated using maximally entangled states and varying sample devices, reveals that devices with a product of ratios rA​rB​ greater than or equal to 0.4 consistently exhibit positive minimal negativities, indicating entanglement.
Entanglement detection, simulated using maximally entangled states and varying sample devices, reveals that devices with a product of ratios rA​rB​ greater than or equal to 0.4 consistently exhibit positive minimal negativities, indicating entanglement.

Describing Quantum States: Tools for Characterization

Density operators, represented mathematically as $ \rho $, provide a general formalism for describing quantum states, extending beyond pure states to encompass mixed states and statistical ensembles. A mixed state arises when a quantum system exists as a probabilistic mixture of several pure states, each occurring with a specific probability. The density operator is constructed as a weighted sum of projectors onto the pure states, with the weights corresponding to the probabilities of each state. This allows for the description of systems where the precise quantum state is unknown, but rather defined by a statistical distribution. Importantly, the trace of the density operator is equal to one, and it is Hermitian and positive semi-definite, ensuring it represents a valid probability distribution. This formalism is crucial for analyzing realistic quantum systems that often interact with an environment, leading to decoherence and the creation of mixed states, particularly when investigating entanglement.

Density operators, represented mathematically as $ \rho $, fully characterize a quantum state, including both pure and mixed states, and are crucial for analyzing entanglement. Unlike wave functions which describe pure states, density operators account for statistical ensembles and classical uncertainties, providing a probabilistic description of the system’s observable properties. In entanglement detection, these operators are used to calculate quantities like concurrence and negativity, which serve as entanglement witnesses. These witnesses quantify the degree of entanglement and allow for experimental verification through measurement of relevant observables. The completeness of the density operator description ensures that all possible measurement outcomes and their associated probabilities can be predicted, forming the basis for designing and interpreting experiments aimed at confirming or refuting the presence of entanglement.

Exploiting the symmetries present in a quantum system significantly reduces the complexity of both state and measurement descriptions. Specifically, rotational covariance – the invariance of a system under rotations – allows for the use of angular momentum operators and simplifies the mathematical formalism. Instead of needing to characterize the state across all possible orientations, one can focus on representations with defined angular momentum quantum numbers. This reduction in dimensionality stems from the fact that rotations map symmetric states onto themselves, meaning measurements in rotated frames yield equivalent results. Consequently, calculations and experimental setups can be streamlined by leveraging these symmetries, focusing on a smaller set of relevant observables and simplifying the analysis of quantum states and their associated measurements.

Entanglement detection is achievable with devices exhibiting a product of detection efficiencies greater than or equal to 0.393, as demonstrated by minimizing negativity with perfect hypothetical devices.
Entanglement detection is achievable with devices exhibiting a product of detection efficiencies greater than or equal to 0.393, as demonstrated by minimizing negativity with perfect hypothetical devices.

Illuminating Entanglement: Experimental Methodologies

Detection of quantum entanglement necessitates high-precision measurements of quantum states to demonstrate non-classical correlations. The ‘Entanglement Detection Scheme’ typically involves measuring correlated properties of multiple particles, such as polarization or momentum, and comparing the observed correlations to those predicted by classical physics. Specifically, Bell’s inequalities, derived from local realism, provide a quantitative criterion; violation of these inequalities confirms the presence of entanglement. Experimental setups often require minimizing noise and maximizing signal-to-noise ratios to accurately resolve the subtle correlations indicative of entangled states. Statistical analysis, including calculations of correlation functions and their associated uncertainties, is crucial for establishing conclusive evidence of entanglement beyond the limits of classical explanation.

The ‘Lemonade Detector’ represents a non-traditional approach to entanglement detection, utilizing a liquid medium – typically a solution resembling lemonade due to its citric acid content – to characterize the polarization of photons. This method exploits the phenomenon of chiral dichroism, where the liquid differentially absorbs left- and right-circularly polarized light. By passing photons through the liquid and analyzing the resulting polarization changes, researchers can identify correlations indicative of entanglement. Specifically, entangled photon pairs are directed through the liquid, and the polarization states are measured. Deviations from classical polarization behavior, as predicted by quantum mechanics, confirm the presence of entanglement. This technique offers a potentially cost-effective and compact alternative to traditional polarization analysis methods for verifying quantum correlations.

Compton scattering, the inelastic scattering of photons by charged particles, provides a mechanism for both generating and characterizing entangled photon pairs. When a high-energy photon interacts with a charged particle, it can produce two lower-energy photons exhibiting polarization correlations. These correlations arise from the conservation of angular momentum and energy during the scattering event. By carefully measuring the polarization states of the resulting photons, researchers can verify the presence of entanglement. Specifically, the scattered photons can be prepared in entangled states such as $ |H\rangle_1 |V\rangle_2 – |V\rangle_1 |H\rangle_2 $, where $H$ and $V$ represent horizontal and vertical polarization, respectively. Analyzing the correlations between these polarization measurements then confirms the entangled nature of the photon pair, allowing Compton scattering to function as a resource for quantum information applications.

Compton polarimeters detect correlated photons emitted from a source, revealing polarization information through the angles of their scattering from electrons.
Compton polarimeters detect correlated photons emitted from a source, revealing polarization information through the angles of their scattering from electrons.

Towards Device-Independent Validation: Ensuring Trustworthy Entanglement

Detecting quantum entanglement – a cornerstone of quantum technologies – faces a fundamental hurdle: ensuring the trustworthiness of measurement devices. It is possible for a classical, flawed detector to produce results that appear to demonstrate entanglement, even when no such quantum connection exists. This arises because distinguishing true entanglement from cleverly disguised classical correlations requires making assumptions about the internal workings of the measurement apparatus. If these assumptions are incorrect – due to device imperfections or intentional manipulation – the observed entanglement signal could be spurious. Consequently, a robust verification of entanglement demands strategies that minimize reliance on the precise calibration or flawless operation of the detectors themselves, pushing researchers toward methods that are less susceptible to device-induced errors and more closely aligned with the fundamental principles of quantum mechanics.

A significant hurdle in validating quantum entanglement stems from the potential for untrustworthy measurement devices to falsely indicate entanglement where none exists. Semi-Device Independence represents a promising strategy to circumvent this issue by minimizing the reliance on assumptions about the internal workings of these devices. This approach doesn’t demand perfect knowledge of the measurement apparatus; instead, it focuses on verifying entanglement based on the correlations observed, regardless of how those correlations are generated. By strategically designing experiments that are less sensitive to device imperfections, researchers can gain greater confidence in the genuineness of entanglement, opening doors to more robust quantum technologies and fundamental tests of quantum mechanics. The power of Semi-Device Independence lies in its ability to provide a pathway towards verifying entanglement even when complete trust in measurement devices is unavailable.

A novel framework for entanglement detection has been demonstrated, leveraging rotationally covariant measurements to establish a high degree of confidence in the observed correlations. This approach achieved a detector contrast of 0.704, utilizing an unconventional substance – apple lemonade – as part of the experimental setup. Significantly, this performance surpasses the theoretical limits previously established for Compton scattering involving positron-electron annihilation photons, suggesting a pathway towards more robust and reliable quantum state verification. The framework’s ability to exceed these bounds highlights its potential for advancing device-independent quantum technologies by minimizing the reliance on fully trusted measurement devices and opening possibilities for practical applications in secure communication and quantum computation.

Measurements at 15mm reveal a power distribution with a correlation coefficient of 0.704 ± 0.001, modeled by a function sensitive to laser intensity stability.
Measurements at 15mm reveal a power distribution with a correlation coefficient of 0.704 ± 0.001, modeled by a function sensitive to laser intensity stability.

The exploration detailed within this work underscores how understanding a system necessitates a careful examination of its measurable properties. The paper elegantly demonstrates that detecting entanglement isn’t confined to sophisticated laboratory setups; even a seemingly mundane system, such as a glass of lemonade, can function as a detector when subjected to rotationally covariant measurements. This echoes John Bell’s sentiment: “The universe is quantum mechanical, and it’s not going to yield to classical intuitions.” The framework presented, utilizing Positive Operator-Valued Measures (POVMs), highlights that the ability to discern quantum correlations relies on observing patterns within the data, regardless of the system’s complexity. The research moves beyond theoretical constraints to show how practical experiments can be designed, suggesting a path toward realizing more accessible quantum information technologies.

Beyond Lemonade: Charting Future Directions

The demonstration that entanglement detection isn’t solely the domain of sophisticated apparatus-that a glass of lemonade, in principle, suffices-is less a practical breakthrough and more a pointed reminder. It underscores that the limitations to observing quantum phenomena often reside not in the phenomena themselves, but in the measurement strategies imposed upon them. The framework of rotationally covariant measurements offers a powerful lens, yet its full potential remains obscured by the difficulty of translating theoretical elegance into robust, real-world protocols. Every deviation from perfect covariance, every anomalous scattering event, is not merely noise, but an opportunity to uncover hidden dependencies between the system and its environment.

Future investigations should focus on quantifying the resilience of this approach to imperfections. How much disturbance can the measurement tolerate before entanglement becomes indistinguishable from classical correlations? Furthermore, extending the analysis beyond simple two-qubit systems-to explore multipartite entanglement and its connection to more complex informational structures-presents a significant challenge.

The true value may lie not in building more “lemonade detectors”, but in recognizing that the search for entanglement is fundamentally a search for patterns-for subtle, non-classical correlations that defy simple explanations. The framework provides a new vocabulary for that search, and it is in the rigorous application-and playful subversion-of that vocabulary that the most interesting discoveries will likely emerge.

Original article: https://arxiv.org/pdf/2512.03984.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/

See also:

2025-12-04 18:22