Author: Denis Avetisyan
This review explores the theoretical landscape of next-generation fractional quantum Hall states, moving beyond established models to characterize exotic topological phases of matter.
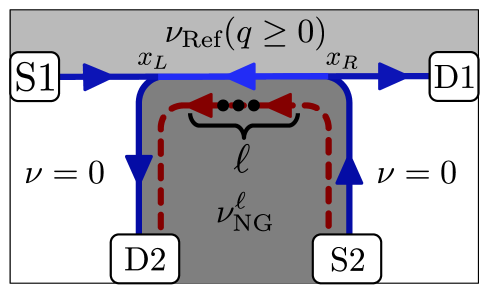
The article details the properties, wavefunctions, and potential experimental signatures of these states, including their thermal Hall conductance and edge state characteristics.
While conventional fractional quantum Hall descriptions struggle to fully capture emerging states beyond simple composite fermion liquids, this work, ‘Theory of Next-Generation Even-Denominator States’, develops a comprehensive theoretical framework for understanding these novel phases. We demonstrate that these ‘next-generation’ states-observed at filling factors like \nu = \frac{3}{4}, \frac{3}{8}, and \frac{3}{10}-possess distinct characteristics from competing phases like Bonderson-Slingerland states, despite sharing identical quasiparticle charges and exchange statistics. Our analysis elucidates experimental signatures in edge transport and bulk properties, alongside detailed wavefunctions and the surprising invariance of interface mode stability under flux attachment. Could these findings pave the way for identifying and characterizing more exotic topological orders in two-dimensional electron systems?
The Emergence of Order: Beyond Conventional Matter
The Fractional Quantum Hall effect demonstrates that matter can exist in states fundamentally different from those traditionally understood, challenging the conventional focus on single-particle properties. When electrons are confined to a two-dimensional plane and subjected to strong magnetic fields at extremely low temperatures, the resulting electronic behavior defies explanation by standard physics. Instead of observing integer-quantized Hall plateaus, experiments reveal plateaus at fractional values, indicating the emergence of quasiparticles with fractional electric charge and statistics. These aren’t mere imperfections or disturbances; they are genuinely new entities – anyons – that neither behave as bosons nor fermions, and whose exchange alters the quantum state of the system. This discovery suggests that the collective behavior of electrons, driven by strong interactions, gives rise to emergent phenomena and novel states of matter with potentially revolutionary applications in quantum technologies.
The emergence of topologically ordered states of matter fundamentally challenges traditional physics, which often focuses on the properties of individual particles. These novel phases aren’t defined by broken symmetries, as with conventional materials, but by the collective, entangled behavior of many particles. Instead of characterizing the system by the properties of its constituents, understanding these states demands a shift in perspective – focusing on the correlations between particles and the resulting emergent phenomena. These correlations give rise to quasiparticles with fractional charge and exotic exchange statistics, properties impossible to explain through single-particle descriptions. It’s this collective behavior, a holistic property of the system, that dictates the unique characteristics and potential applications of topologically ordered matter, opening new avenues for materials science and quantum technologies.
The emergence of exotic states of matter, like those observed in the Fractional Quantum Hall effect, is critically governed by the `FillingFactor`, a ratio defining the number of electrons relative to the available magnetic flux quanta. This parameter doesn’t simply influence whether a novel phase appears, but actively sculpts the landscape of possible emergent phenomena. At specific fractional values – such as 1/3, 2/5, or 5/2 – the intricate interplay of electron-electron interactions leads to the formation of quasiparticles with fractional charge and unusual exchange statistics. Altering the `FillingFactor` is akin to tuning a dial, revealing a rich tapestry of topological order and allowing researchers to explore fundamentally new forms of matter governed by collective behavior rather than individual particle properties. This precise control offered by the `FillingFactor` makes these systems ideal platforms for both fundamental research and the potential development of robust quantum technologies.
Topological order offers a pathway toward remarkably stable quantum computation. Unlike conventional qubits, which are easily disrupted by environmental noise, topologically protected qubits encode information not in individual particles, but in the global properties of the system – specifically, in the way particles are braided around each other. This means that local disturbances, such as stray electromagnetic fields or particle interactions, cannot easily corrupt the encoded quantum information; the information is distributed and protected by the topology of the system itself. This inherent robustness stems from the fact that altering the information requires a large-scale, coordinated change, rather than a local perturbation. Consequently, these states hold significant promise for building fault-tolerant quantum computers capable of performing complex calculations with unprecedented reliability, representing a major leap forward in the field of quantum information processing.
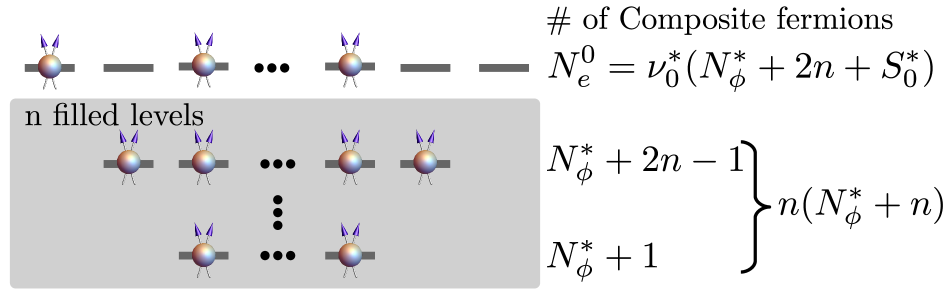
Evidence of Anyonic Behavior: The 5/2 State
The filling fraction ν = 5/2 state in the fractional quantum Hall effect demonstrates non-Abelian statistics, meaning that the exchange of two quasiparticles does not simply acquire a phase factor, but undergoes a more complex transformation represented by a matrix. This contrasts with fermions and bosons which exhibit exchange statistics governed by factors of -1 or +1, respectively. Specifically, the 5/2 state supports quasiparticles with anyonic statistics, where the exchange operation results in a unitary transformation within a degenerate ground state manifold. The degeneracy of this manifold is related to the number of filled Landau levels and is directly observable in transport measurements. This non-Abelian behavior arises from the collective many-body interactions and topological order inherent in the system, making the 5/2 state a prominent example for investigations into topological quantum computation.
The \nu = 5/2 quantum Hall state is accurately described by the HaldaneMooreRead (HMR) composite fermion theory utilizing a Pfaffian wavefunction. This wavefunction, antisymmetric for any pair of electrons, accounts for the observed fractional statistics – specifically, any two quasiparticles exhibit exchange statistics differing from both bosons and fermions. The Pfaffian wavefunction, expressed as a determinant of a skew-symmetric matrix, mathematically captures the correlated pairing of electrons necessary to form these anyonic excitations. Crucially, the HMR description predicts a zero-energy mode localized at impurities, a characteristic experimentally verified and confirming the topological order inherent in the 5/2 state and the validity of the Pfaffian ansatz.
Experimental verification of the 5/2 state and the Pfaffian wavefunction relies heavily on characterizing the behavior of edge states in quantum Hall devices. These states, localized at the physical boundaries of the two-dimensional electron gas, exhibit conductance quantization in units of e^2/h. Precise measurements of these conductance values, alongside tunneling experiments probing the fractional charge and statistics of quasiparticles at the edges, provide crucial evidence for the non-Abelian nature of the 5/2 state. Specifically, the observation of a 1/2 conductance anomaly, and the suppression of backscattering, strongly support the theoretical predictions derived from the Pfaffian wavefunction, differentiating it from Abelian states and confirming the presence of Majorana modes within the edge states.
The successful characterization of the 5/2 state and its description via the ν = 5/2 Pfaffian wavefunction establishes a methodology for investigating other non-Abelian fractional quantum Hall states. These more complex states, observed at filling fractions beyond 5/2, often exhibit increased topological order and more intricate quasiparticle excitation spectra. The techniques developed for probing edge states and characterizing the fusion rules of quasiparticles in the 5/2 state are directly applicable – though requiring refinement for the specific symmetry and filling fraction – to these higher-order states. This allows researchers to move beyond the relatively simple 5/2 case and map out the landscape of topological order in two-dimensional electron systems, potentially leading to the discovery of states suitable for topological quantum computation.
Probing the Invisible: Experimental Techniques
Fractional quantum Hall (FQH) states are characterized by conducting edge states that are fundamentally different from those found in integer quantum Hall systems. These edge states, arising from the gapped bulk and topologically protected boundary conditions, exhibit fractional charge and statistics. Experimental investigation of these edge states relies on techniques such as measuring conductance as a function of magnetic field and temperature, and observing the quantization of conductance in multiples of e^2/h. Precise control of sample geometry, low-temperature environments (typically in the milliKelvin range), and high magnetic fields are essential for isolating and characterizing the chiral edge modes and detecting signatures of the underlying topological order. Further analysis often involves examining the robustness of these edge states to perturbations, such as impurities or disorder, to confirm their topological protection.
Characterizing topological order in fractional quantum Hall states relies on sensitive electrical transport measurements. Upstream noise measurements detect current fluctuations arising from tunneling events between quantum Hall edges, providing information about the edge state properties and revealing the presence of fractional charges. Scaling of tunneling currents, specifically analyzing the current-voltage relationship of tunneling junctions, allows for the determination of fractional charge and the identification of non-Abelian statistics. Finally, coherent conductance measurements, performed on constrictions or quantum point contacts, probe the transmission probabilities of edge states and can differentiate between different topological phases based on the number of conducting edge modes and their chiralities; the measured conductance is quantized in units of e^2/h and directly reflects the topological properties of the system.
The KK matrix formalism provides a mathematical framework for characterizing the low-energy quasiparticle excitations in topologically ordered systems. This approach directly links theoretical predictions about quasiparticle content – including their quantum numbers, fusion rules, and braiding statistics – to experimentally measurable quantities. Specifically, the KK matrix relates the topological sector labels to the corresponding degenerate ground states, allowing for the calculation of transport coefficients and response functions. By comparing experimentally determined KK matrix elements with theoretical models, researchers can verify the presence of non-Abelian anyons and determine the underlying topological order of the system. This methodology is crucial for validating theoretical predictions and interpreting experimental results in the field of topological quantum matter.
Thermal Hall conductance measurements are a key experimental probe of neutral excitations in topological systems, allowing for differentiation between distinct topological phases. This quantity, \kappa_{xy} , is sensitive to the properties of these excitations, particularly their chirality and pairing channel. Specifically, the calculated value of \kappa_{xy} is directly dependent on the nature of the edge modes – their chiralities (whether they propagate in a specific direction) and the pairing symmetry of the underlying excitations. Different topological phases exhibit unique thermal Hall signatures due to variations in these edge mode characteristics, providing a means for experimental identification and characterization beyond conventional charge transport measurements.
Beyond the Known: New Frontiers in FQH Physics
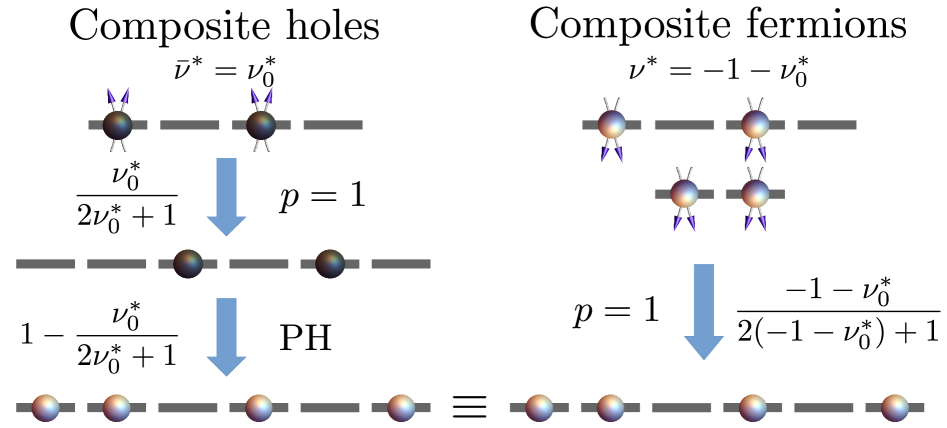
The pursuit of understanding the fractional quantum Hall effect (FQHE) has revealed a landscape extending beyond the well-established Jain sequence of states. These so-called “NextGenerationStates” exhibit properties not predicted by current theoretical frameworks, necessitating a deeper exploration of electron correlations in two-dimensional systems. Characterized by fractionalized excitations and exotic topological order, these states challenge conventional descriptions of electron behavior and hint at fundamentally new phases of matter. The emergence of these states isn’t merely an incremental addition to existing knowledge; it signals a need for innovative theoretical approaches capable of capturing the intricate interplay of interactions and symmetries that govern their formation. Research suggests these states could potentially unlock pathways to novel quantum technologies, leveraging their unique properties for robust quantum computation and information storage, but first, a complete theoretical understanding must be achieved.
The emergence of fractional quantum Hall states beyond the conventional Jain sequence suggests the possibility of entirely new forms of electron pairing, potentially leading to the creation of paired superfluids. Unlike conventional superconductivity, which relies on Cooper pairs formed from electrons with opposite momentum and spin, these novel states propose more exotic pairing mechanisms. Theoretical investigations indicate that these paired states aren’t limited to simple pairings; instead, they could involve more complex correlations, influencing the emergent properties of the electron system. This shift in pairing behavior could manifest as unconventional superconductivity, characterized by unusual temperature dependencies, gap structures, and responses to external fields – potentially opening pathways to materials with unprecedented superconducting characteristics and applications. The exploration of these paired superfluids represents a significant frontier in condensed matter physics, challenging established paradigms and offering a glimpse into the rich diversity of quantum matter.
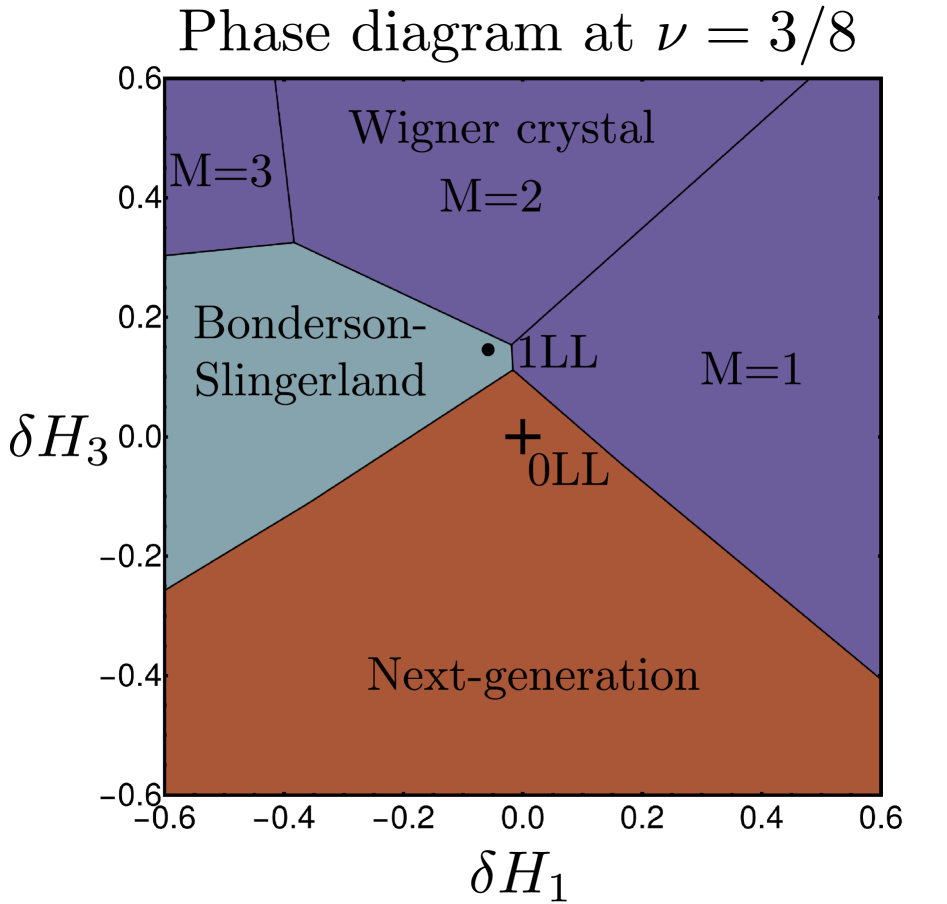
The emergence of novel fractional quantum Hall states beyond the Jain sequence necessitates exploration of theoretical frameworks capable of describing their exotic properties, and models based on Bonderson-Slingerland states offer a promising avenue. These non-Abelian states, characterized by topologically protected zero modes, provide a potential explanation for the observed unconventional behavior, particularly the emergence of anyonic excitations with fractional statistics. The framework predicts a rich phase diagram with various topological orders, potentially accounting for experimental observations of plateaus at fractional filling fractions not explained by conventional Laughlin or Jain sequences. Calculations within this framework suggest that the peculiar behavior arises from the collective interactions of these anyons, leading to unique transport properties and a departure from the standard paradigm of single-particle excitations, offering a pathway to understanding these newly discovered quantum phases of matter.
The pursuit of understanding NextGenerationStates in fractional quantum Hall physics necessitates exploration beyond conventional frameworks, potentially requiring a reassessment of the electron system’s fundamental organization. Theoretical investigations suggest that, in certain regimes, electrons may not behave as a uniform fluid but instead coalesce into spatially ordered phases like Wigner crystals or charge density wave states. These alternative arrangements are mathematically described by complex Ψ wavefunctions, which, when analyzed, predict fractional quantum Hall plateaus at unusual filling factors – specifically, calculated shifts ranging from 7/3 to 11/6. These non-integer values deviate from the Jain sequence and hint at novel interactions and emergent phenomena within the two-dimensional electron gas, demanding new theoretical tools and experimental probes to fully characterize these exotic states of matter.
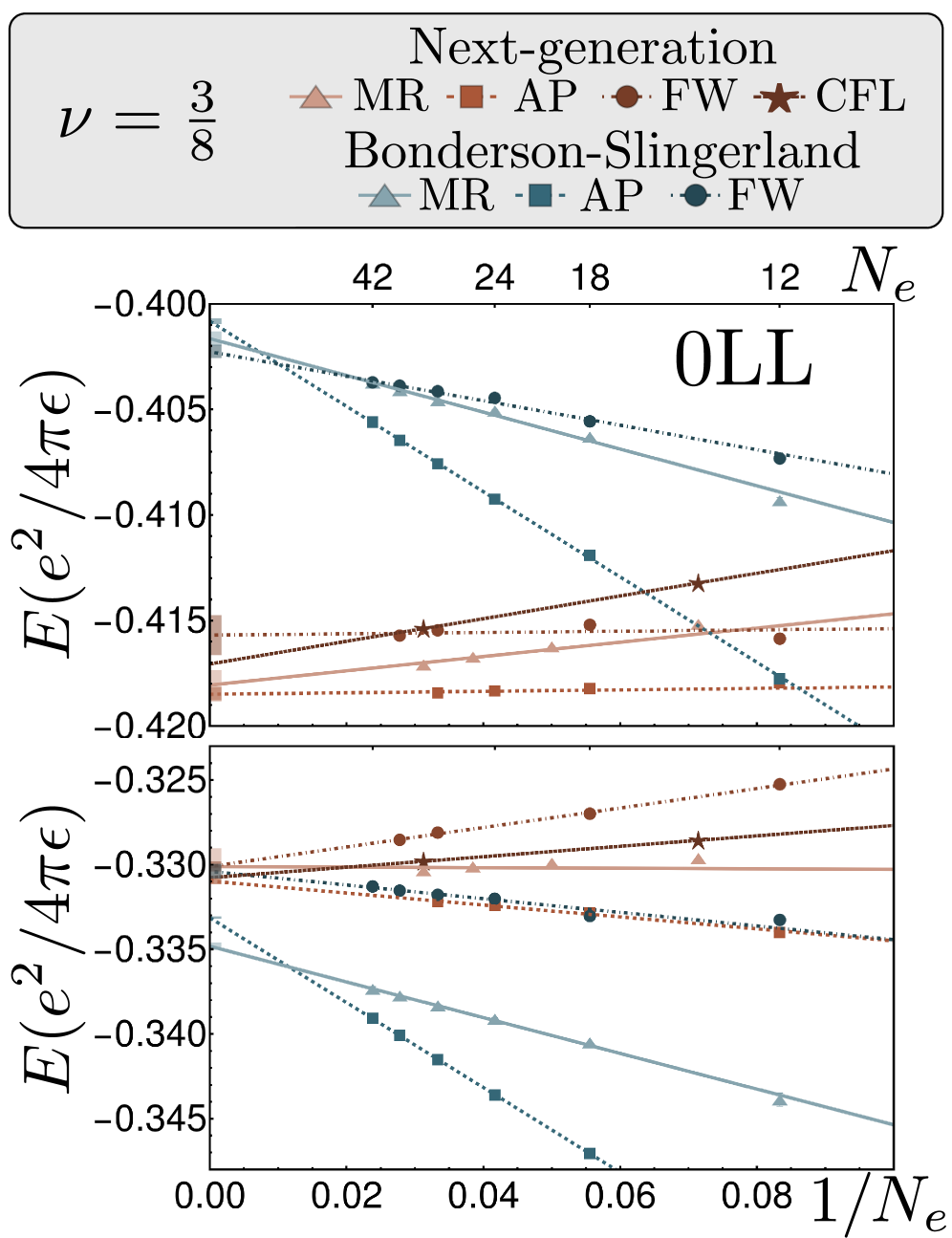
The pursuit of differentiating next-generation fractional quantum Hall states demands rigorous simplification. This work, concerning even-denominator states and their topological order, benefits from stripping away extraneous complexity to reveal underlying structure. One recalls René Descartes’ assertion: “It is not enough to have a good mind; the main thing is to use it well.” The exploration of thermal Hall conductance and edge states, as detailed within, isn’t about amassing data, but judiciously applying theoretical tools. The true signature of these states-the unique wavefunction characteristics-emerges not from complication, but from clarity of definition.
What Remains to be Seen
The pursuit of even-denominator fractional quantum Hall states, as detailed within, is not merely a search for novel quantum fluids. It is, at its core, a refinement of the question: what constitutes a truly robust topological order? Existing theoretical frameworks, while predictive, often rely on extrapolations from composite fermion pictures. The value lies not in extending these frameworks, but in recognizing their inherent limitations. Future investigations must prioritize the development of genuinely variational wavefunctions, unburdened by pre-conceived notions of quasi-particle statistics.
The experimental landscape demands a more nuanced interrogation of thermal Hall conductance. Current measurements, while suggestive, remain susceptible to contributions from phonon transport and sample disorder. Distinguishing between genuinely topological edge states and trivial excitations will require an order of magnitude improvement in measurement precision, and perhaps, a fundamental shift in experimental design. The signal, after all, is not louder with more noise.
Ultimately, the differentiation of these states-Bonderson-Slingerland or otherwise-is less a matter of identifying a unique fingerprint and more a process of rigorous exclusion. Each observed characteristic serves to narrow the possibilities, to subtract potential explanations until only the essential remains. The goal is not a more complex theory, but a simpler truth.
Original article: https://arxiv.org/pdf/2601.15386.pdf
Contact the author: https://www.linkedin.com/in/avetisyan/
See also:
- Best Controller Settings for ARC Raiders
- Donkey Kong Country Returns HD version 1.1.0 update now available, adds Dixie Kong and Switch 2 enhancements
- How To Watch A Knight Of The Seven Kingdoms Online And Stream The Game Of Thrones Spinoff From Anywhere
- Ashes of Creation Rogue Guide for Beginners
- PS5’s Biggest Game Has Not Released Yet, PlayStation Boss Teases
- When to Expect One Piece Chapter 1172 Spoilers & Manga Leaks
- Sega Insider Drops Tease of Next Sonic Game
- New Netflix Movie Based on Hugely Popular Book Becomes An Instant Hit With Over 33M Hours Viewed
- Darkwood Trunk Location in Hytale
- Hytale: Upgrade All Workbenches to Max Level, Materials Guide
2026-01-24 04:45