Author: Denis Avetisyan
New research explores how non-equilibrium effects influence the transport properties of hadronic matter, impacting our understanding of the quark-gluon plasma and heavy-ion collisions.
This review details how Tsallis statistics, applied within the Fokker-Planck equation, modifies drag and diffusion coefficients for hadrons in a non-equilibrium medium.
While conventional descriptions of the quark-gluon plasma often assume thermal equilibrium, the highly energetic hadronic medium created in heavy-ion collisions likely deviates from this idealization. This work, ‘Influence of Non-extensivity on the drag and diffusion coefficients of hadronic matter’, investigates the transport properties of hadrons within this non-equilibrium environment using the Fokker-Planck equation and Tsallis nonextensive statistics. Our analysis reveals that drag and diffusion coefficients are significantly impacted by both temperature and the degree of non-equilibrium, as well as the inclusion of heavier hadronic resonances. Understanding these effects is crucial for accurately modeling the thermal and dynamical evolution of the hadronic phase preceding freezeout-how might these non-equilibrium dynamics ultimately influence our interpretation of collective behavior in these extreme conditions?
The Primordial Echo: Probing the Quark-Gluon Plasma
The quest to understand the universe’s infancy and the dense cores of neutron stars necessitates investigation into the quark-gluon plasma (QGP), a truly exotic state of matter. Predicted by quantum chromodynamics, the theory governing the strong nuclear force, the QGP emerges when matter is heated to trillions of degrees Celsius – conditions mirroring those fractions of a second after the Big Bang. At such extreme temperatures, protons and neutrons dissolve into their constituent quarks and gluons, forming a fluid-like soup where these particles move freely. Studying the QGP isn’t merely an academic exercise; it offers a unique window into the fundamental forces shaping reality and the evolution of the cosmos, providing crucial insights into the building blocks of matter itself and the conditions that governed the universe’s earliest moments.
Heavy mesons, subatomic particles composed of a quark and an antiquark, function as invaluable tools for investigating the quark-gluon plasma (QGP). Their interaction with the dense, intensely hot QGP reveals crucial insights into this primordial state of matter, yet accurately deciphering their behavior is profoundly complex. As these mesons traverse the QGP, they undergo various interactions – including scattering, absorption, and recombination – altering their momentum and number. A comprehensive understanding of these interactions, which are influenced by the QGP’s transport properties and internal dynamics, is essential for correctly interpreting experimental data. Failing to account for the nuances of these meson-medium interactions could lead to misinterpretations of the QGP’s temperature, viscosity, and overall composition, hindering progress in unraveling the mysteries of the early universe and the extreme conditions found within neutron stars.
Current investigations into the quark-gluon plasma frequently rely on models that presume a state of thermal equilibrium, a simplification that may inadvertently mask the complex, rapidly evolving dynamics inherent to this extreme environment. While computationally efficient, these equilibrium approaches struggle to capture the non-equilibrium effects arising from the QGP’s creation and subsequent transition into hadronic matter. This is particularly relevant when analyzing the behavior of heavy mesons, as their interactions with the surrounding medium are sensitive to these transient conditions. A more nuanced understanding requires theoretical frameworks capable of describing the QGP as a far-from-equilibrium system, acknowledging the fleeting correlations and collective flows that characterize its initial stages and influence the formation of observable hadrons.
Beyond Static Equilibrium: Modeling Hadronic Interactions
The evolution from the Quark-Gluon Plasma (QGP) to a hadronic medium is not a smooth, instantaneous process occurring at complete thermodynamic equilibrium. Evidence suggests rapid changes in temperature and density, leading to deviations from equilibrium conditions. Standard statistical descriptions, such as the Boltzmann-Gibbs framework, assume equilibrium and rely on exponential distributions of particle momenta and energies. These models fail to accurately represent the observed particle spectra in heavy-ion collisions, particularly at high transverse momenta. The non-equilibrium state necessitates the use of statistical frameworks that can account for long-range correlations and deviations from exponential behavior, requiring a departure from the assumptions inherent in traditional Boltzmann statistics to effectively model the resulting hadronic phase.
Tsallis statistics represent a non-extensive generalization of Boltzmann-Gibbs statistics, utilizing a q-parameter to modify the usual exponential distribution. Unlike traditional approaches which assume equilibrium, Tsallis statistics account for systems with long-range interactions or correlations, frequently observed during the transition from the quark-gluon plasma to hadronic matter. The resulting particle distributions are parameterized by a power-law behavior, enabling a more accurate description of high-transverse momentum spectra and enhanced particle production commonly seen in heavy-ion collisions. Specifically, the Tsallis distribution takes the form f(p) \propto [1 + (p/T)^2]^{-q/2}, where p is the particle momentum, T is the temperature, and q quantifies the degree of non-extensivity; a value of q=1 recovers standard Boltzmann statistics.
The application of Tsallis statistics to the hadronic medium allows for the modeling of deviations from standard thermal behavior expected during the transition from the quark-gluon plasma. This approach utilizes a non-extensive q-parameter which modifies the particle distribution function, effectively altering observed particle multiplicities and transverse momentum spectra. Specifically, values of q greater than one indicate enhanced production of high-transverse momentum particles, while values less than one suppress them relative to a Boltzmann distribution. Empirical fitting of experimental data from heavy-ion collisions demonstrates that the q-parameter is not constant across particle species, indicating that different hadrons experience the non-equilibrium effects of the transition to varying degrees, and that the parameter is sensitive to collision energy and system size.
Mapping the Dynamics: Particle Trajectories in a Dense Medium
The Fokker-Planck equation is a partial differential equation used to model the time evolution of the probability distribution function for particles subject to random forces. In the context of heavy meson dynamics within a hadronic medium, it provides a theoretical framework to describe the stochastic processes of momentum transfer and energy loss experienced by these particles. The equation accounts for both deterministic forces, such as the average interaction with the medium, and stochastic forces representing the numerous uncorrelated interactions. Specifically, the solution to the Fokker-Planck equation yields the probability of finding a heavy meson with a particular momentum at a given time as it propagates through the dense medium, allowing for quantitative predictions of its behavior. \frac{\partial f}{\partial t} = -v \frac{\partial f}{\partial x} + \frac{\partial}{\partial p} \left[ A(p) f \right] + \frac{\partial^2}{\partial p^2} \left[ B(p) f \right] , where f is the distribution function, v is the particle’s velocity, and A and B represent the friction and diffusion coefficients, respectively.
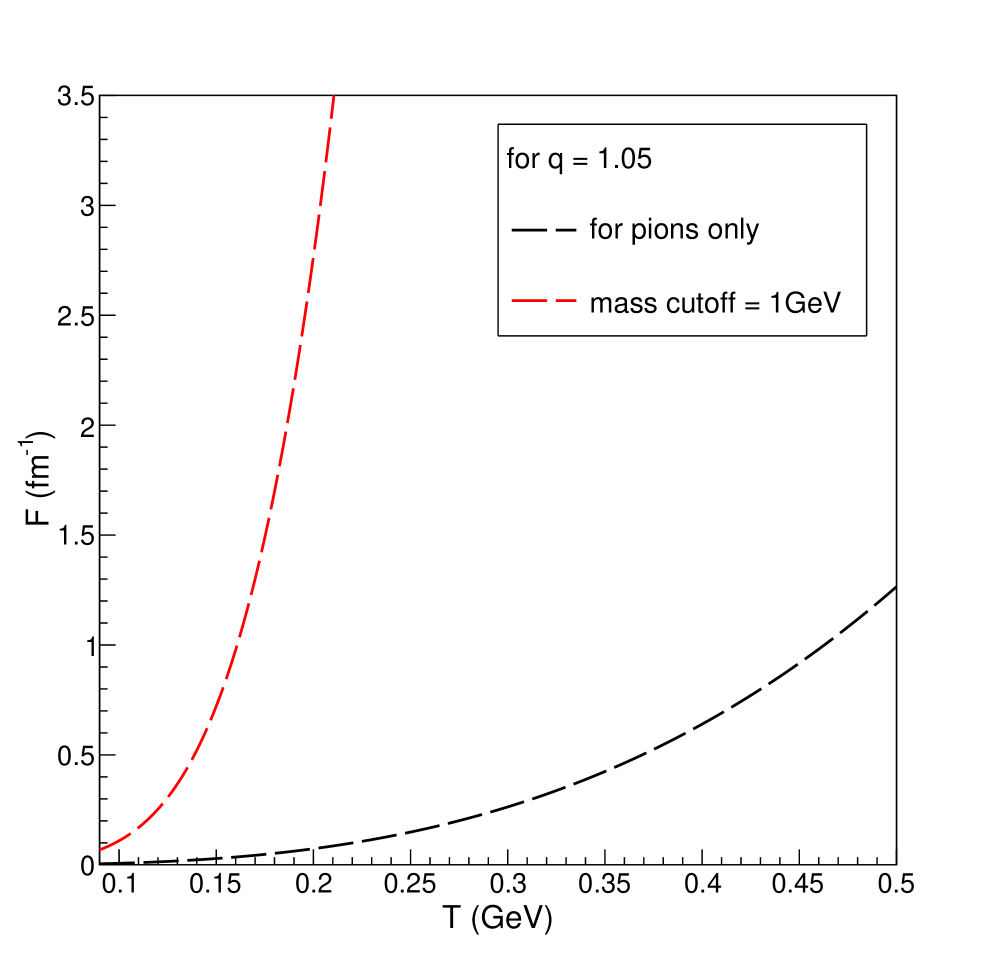
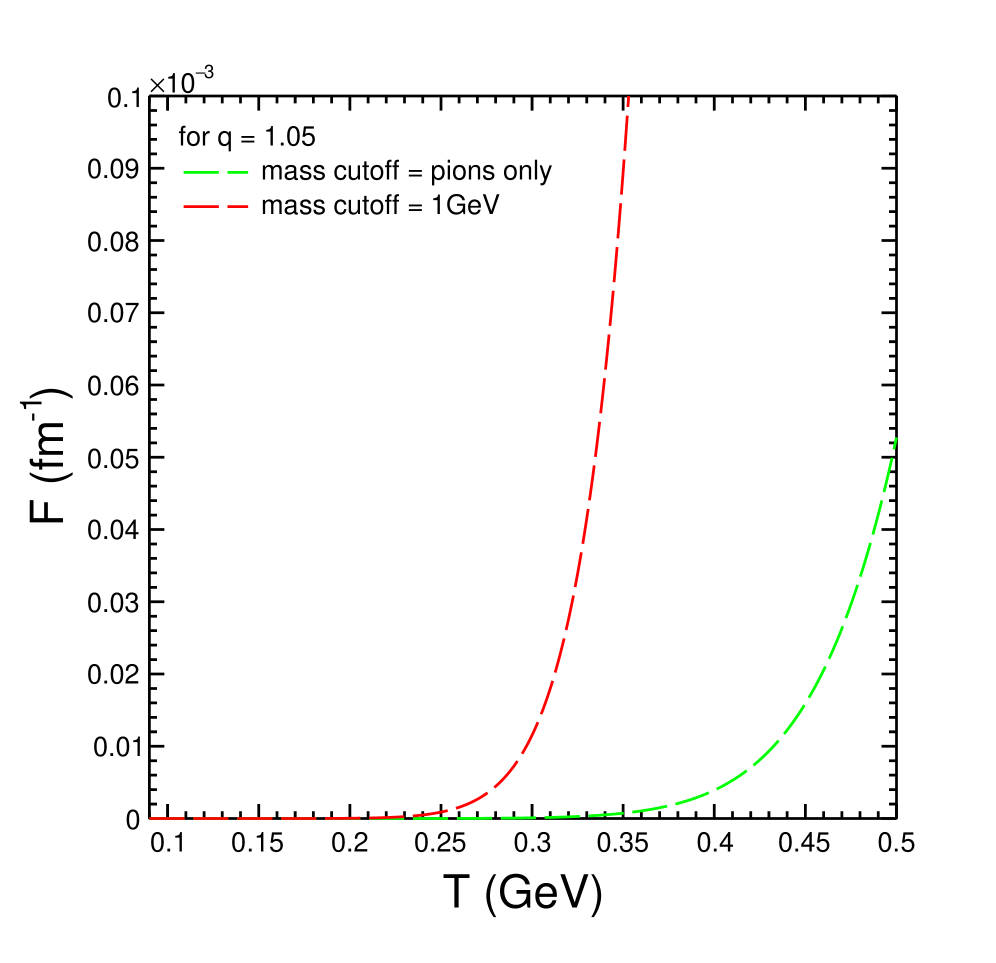
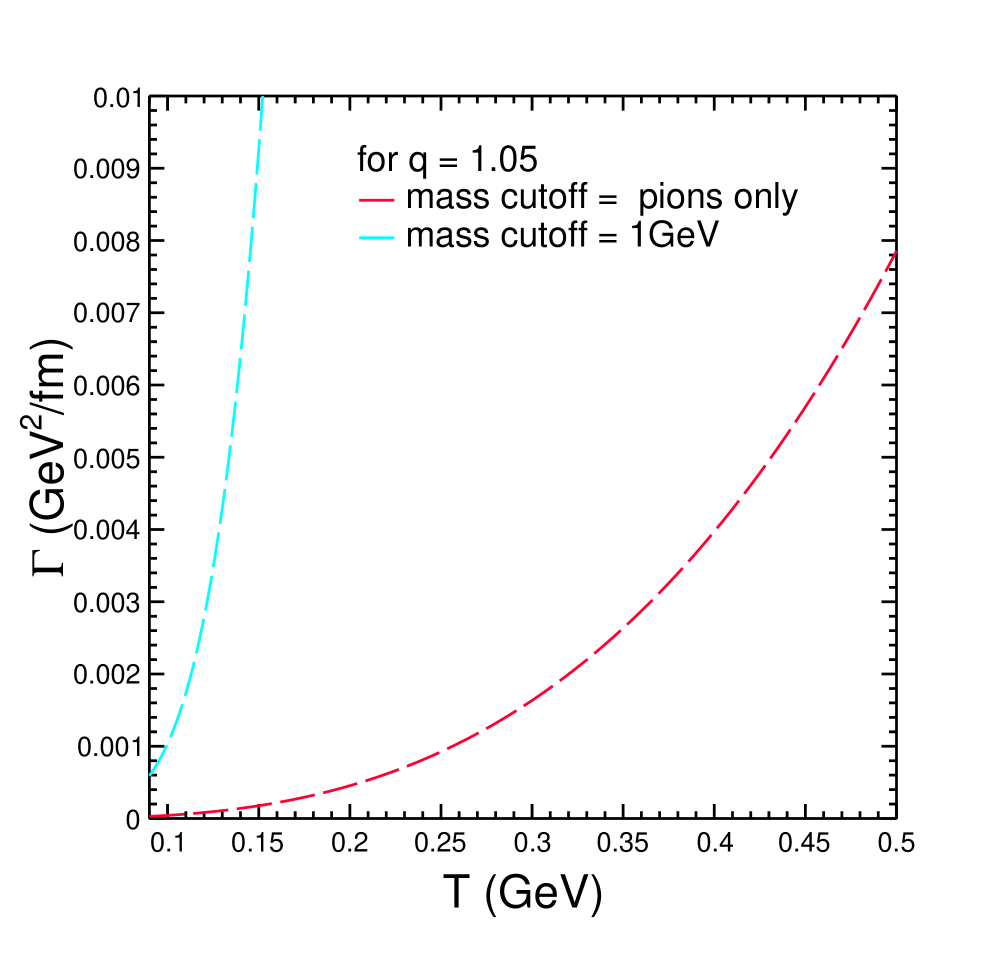
Within the Fokker-Planck equation, the drag coefficient Γ represents the average rate of momentum loss experienced by a heavy meson due to interactions with the surrounding hadronic medium. A larger Γ indicates a more rapid deceleration. Conversely, the momentum diffusion coefficient D quantifies the rate of random momentum transfer; it describes the fluctuations in momentum induced by collisions and scattering processes. A higher D signifies increased stochasticity in the meson’s trajectory. These coefficients are not independent; the ratio D / \Gamma determines the characteristic scale of momentum fluctuations relative to the rate of momentum loss, influencing the overall transport behavior of the heavy meson within the medium.
Analysis of heavy meson dynamics within the hadronic medium demonstrates an exponential relationship between the drag and momentum diffusion coefficients, and several key parameters. Specifically, both coefficients increase exponentially with rising temperature, the Tsallis ‘q’ parameter – which governs the degree of non-equilibrium – and increasing hadronic mass cutoff. This behavior suggests a strengthened coupling between the heavy meson and the medium constituents, leading to more frequent and substantial random momentum exchanges. Quantitatively, higher temperatures and larger mass cutoffs directly contribute to increased collision rates, while a larger Tsallis ‘q’ parameter indicates enhanced long-range correlations and a greater deviation from thermal equilibrium, both intensifying the random momentum transfer and thus elevating both the drag and diffusion coefficients. D \propto e^{\alpha T} and \Gamma \propto e^{\beta T}, where D is the drag coefficient, Γ is the momentum diffusion coefficient, and α and β are constants dependent on the hadronic mass cutoff and the Tsallis ‘q’ parameter.
Revealing the Medium’s Signature: Quantifying Properties and Limitations
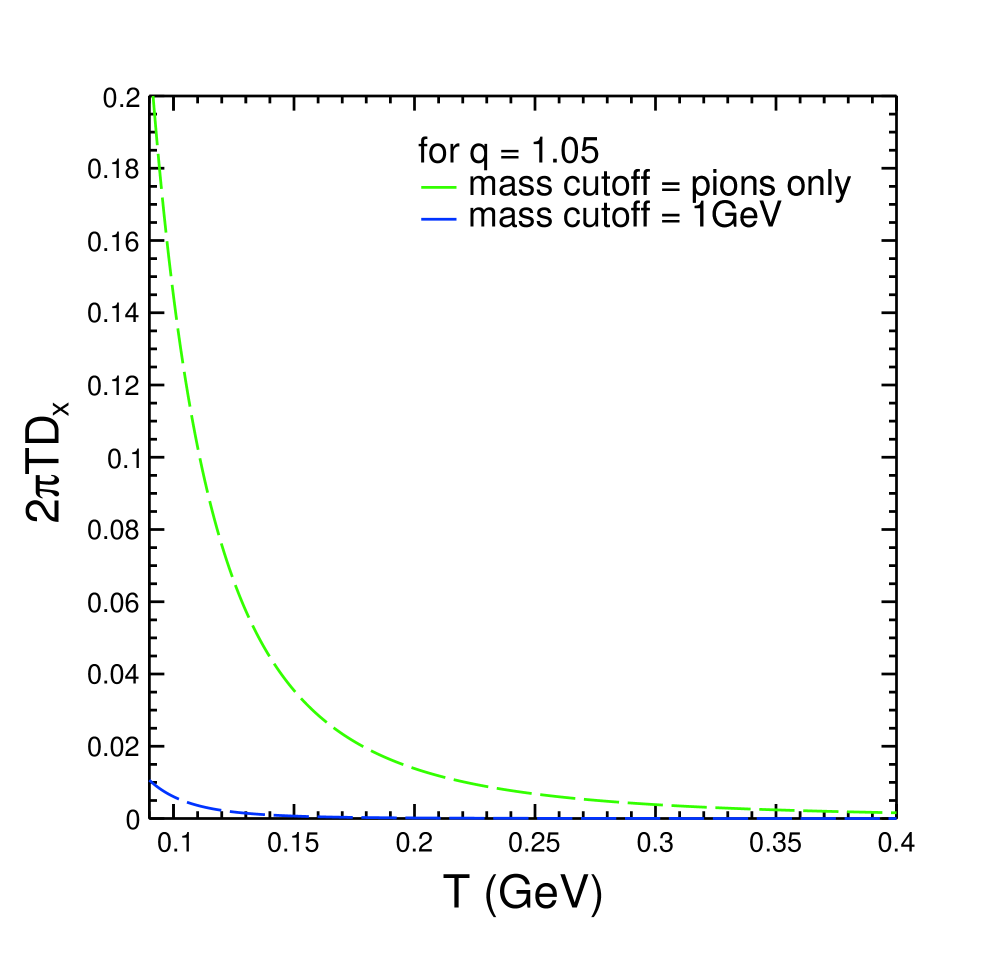
The spatial diffusion coefficient, calculated through the Fokker-Planck equation, quantifies the rate at which heavy mesons disperse within the dense hadronic medium. A decreasing value of this coefficient with increasing temperature, momentum transfer q, and mass cutoff signifies a strengthening of confinement – essentially, a greater resistance to the meson’s movement and a tendency to remain localized. This behavior suggests that as the medium becomes hotter or more dense, or as higher momentum interactions are considered, the heavy mesons experience increased interactions that restrict their spatial spread. Consequently, the diffusion coefficient serves as a sensitive probe of the medium’s properties, revealing details about the forces governing the behavior of these short-lived particles and providing insights into the nature of confinement in quantum chromodynamics.
The drag coefficient plays a crucial role in understanding how heavy quarks traverse the quark-gluon plasma, directly impacting the observed distributions of heavy mesons. This coefficient quantifies the resistance the medium exerts on moving particles, governing both the rate at which they lose energy and transfer momentum to the surrounding plasma constituents. A precise determination of this value is therefore essential for accurately modeling the suppression of heavy meson production in relativistic heavy-ion collisions; underestimations would lead to an overprediction of particle yields, while overestimations would mask the true extent of medium effects. Consequently, refined calculations and experimental measurements focused on the drag coefficient are vital for unraveling the transport properties of the strongly coupled plasma and gaining deeper insights into the dynamics of heavy quark diffusion, influencing the overall interpretation of collision data and the reconstruction of the plasma’s evolution.
Analysis reveals a consistent relationship between the timescales for energy loss experienced by different heavy mesons within the hadronic medium. Specifically, the relaxation time – a measure of how quickly a meson loses momentum – is approximately 2.3 to 2.9 times longer for J/ψ mesons compared to D0 mesons, and 1.6 to 1.9 times longer for Υ mesons relative to D0 mesons. Importantly, this ratio remains remarkably stable across the temperature range investigated, indicating that the suppression of heavier quarkonia – like J/ψ and Υ – relative to lighter ones, such as D0, is a robust phenomenon tied to intrinsic properties of the quarkonia themselves, rather than being significantly influenced by temperature fluctuations within the medium. This suggests a predictable pattern of heavy quark suppression that can be leveraged in understanding the dynamics of the quark-gluon plasma.
The study of hadronic matter’s transport properties, as detailed in this work, highlights the inherent temporality of physical models. Each iteration-incorporating Tsallis statistics, heavier resonances, or refinements to the Fokker-Planck equation-represents a temporary approximation of a perpetually evolving system. As Hannah Arendt observed, “The moment we begin to think, we are already old,” suggesting that even the genesis of understanding is rooted in a pre-existing condition. This resonates with the article’s approach, where adjustments to drag and diffusion coefficients aren’t definitive answers but rather successive refinements acknowledging the medium’s non-equilibrium dynamics and the limitations of current abstraction.
The Inevitable Drift
The exploration of hadronic transport via non-extensive statistical mechanics, as undertaken in this work, reveals not so much new physics as a refined understanding of its inherent limitations. The Fokker-Planck equation, a tool built on assumptions of gradual change, remains a useful, if ultimately temporary, scaffolding for describing systems destined for decay. The influence of Tsallis statistics, while offering a means to account for non-equilibrium effects, does not halt the march toward disorder; it merely shifts the parameters by which that disorder manifests. The inclusion of heavier resonances, a necessary complication, simply delays the inevitable fragmentation of the system.
Future work will undoubtedly focus on extending this framework, perhaps incorporating more sophisticated models of particle interactions or attempting to bridge the gap between theoretical descriptions and experimental observations of the quark-gluon plasma. Yet, it is crucial to acknowledge that increased complexity does not guarantee lasting accuracy. Each added layer of detail introduces new avenues for error, and the pursuit of perfect fidelity is, in essence, a chase after a receding horizon.
The true challenge lies not in perfecting the description of the present state, but in understanding the nature of the transition itself. Systems do not fail because of specific flaws; they age because time is inevitable. Stability, in many instances, is simply a prolonged postponement of the ultimate disintegration, a temporary equilibrium masking the underlying entropy.
Original article: https://arxiv.org/pdf/2602.05478.pdf
Contact the author: https://www.linkedin.com/in/avetisyan/
See also:
- Best Controller Settings for ARC Raiders
- DCU Nightwing Contender Addresses Casting Rumors & Reveals His Other Dream DC Role [Exclusive]
- 7 Home Alone Moments That Still Make No Sense (And #2 Is a Plot Hole)
- Stephen Colbert Jokes This Could Be Next Job After Late Show Canceled
- Is XRP ETF the New Stock Market Rockstar? Find Out Why Everyone’s Obsessed!
- 10 X-Men Batman Could Beat (Ranked By How Hard It’d Be)
- Supergirl Trailer Shows 1 Thing DCU Movie Does Better Than Woman of Tomorrow Comic
- Ashes of Creation Rogue Guide for Beginners
- Ghostbusters Star Confirms the Weirdest Cameo in Franchise History Is Actually Canon to the Movies
- Gold Rate Forecast
2026-02-08 09:51