Author: Denis Avetisyan
New research provides an exact description of how entanglement evolves following a disturbance in an integrable free-fermion model.
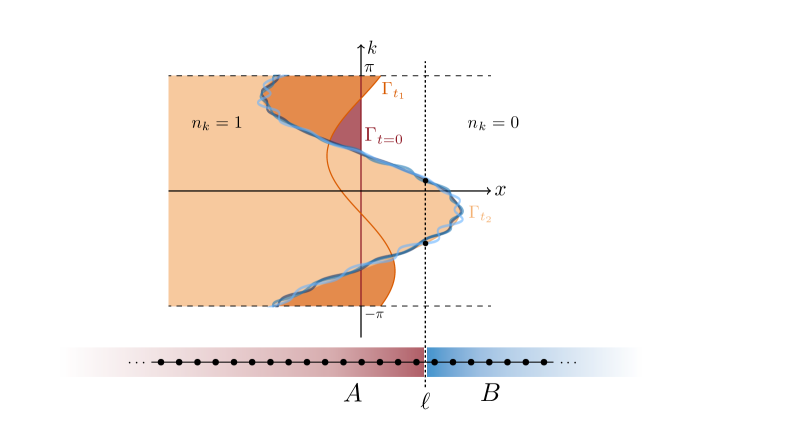
This study extends quantum generalized hydrodynamics to characterize non-equilibrium dynamics and reveals diffusive behavior in the $ν= 1$ QSSEP model.
Understanding non-equilibrium dynamics in many-body systems remains a central challenge in modern physics, particularly when stochastic effects are present. This work, ‘Inhomogeneous quenches and GHD in the $ν= 1$ QSSEP model’, extends the framework of quantum generalized hydrodynamics (GHD) to investigate the out-of-equilibrium behavior of a stochastic one-dimensional free-fermion system undergoing inhomogeneous quenches. We demonstrate an exact characterization of entanglement spreading and reveal diffusive behavior at large space-time scales, incorporating quantum fluctuations via conformal field theory. Does this extension of GHD to stochastic systems offer a pathway towards understanding broader classes of open quantum systems and their emergent dynamics?
The Quantum Mess: Why Simulating Reality is Always a Hack
The pursuit of understanding how quantum systems evolve – their dynamics – remains a cornerstone of modern physics, presenting a formidable challenge due to the inherent complexities of quantum mechanics and the interactions between multiple particles. Unlike classical systems, where predicting future behavior is often straightforward, quantum systems are governed by probabilities and exhibit phenomena like superposition and entanglement, dramatically increasing the computational difficulty. This is particularly true when considering many-body systems – those comprised of numerous interacting quantum particles – where traditional analytical and numerical methods frequently falter. The difficulty isn’t simply one of scale; it’s a fundamental shift in the nature of the problem, demanding new theoretical frameworks and computational tools to accurately model and predict the behavior of matter at its most fundamental level. This need drives ongoing research into innovative approaches for simulating and understanding these complex quantum dynamics, ultimately aiming to unlock a deeper understanding of the universe and its building blocks.
The investigation of many-body quantum systems presents a significant hurdle for conventional computational approaches. These systems, comprised of numerous interacting quantum particles, quickly become analytically intractable as their size increases, leading to an exponential growth in computational demand. Traditional methods, often reliant on perturbative expansions or mean-field approximations, frequently falter when applied to scenarios far from equilibrium, where these approximations break down. Such conditions – crucial for understanding phenomena like driven systems, quantum quenches, and open quantum systems – demand techniques capable of capturing strong correlations and non-equilibrium dynamics. The inability of established methods to accurately model these complex interactions motivates the development of novel theoretical and numerical tools, aiming to overcome the limitations imposed by the inherent complexity of quantum many-body physics and accurately describe systems evolving away from stable, predictable states.
The Quantum Symmetric Simple Exclusion Process (QSSEP) serves as a valuable theoretical framework for investigating the intricate dynamics of many-body quantum systems, particularly those lacking equilibrium. This model, though conceptually simple, presents significant computational challenges due to the inherent complexity of quantum interactions and correlations. A key characteristic of QSSEP is its unique entanglement entropy scaling, described by S(t) \sim log(t), where the entropy grows logarithmically with time. This logarithmic scaling indicates a spreading of quantum correlations that differs fundamentally from classical systems and necessitates the development of novel analytical and numerical techniques capable of accurately capturing this behavior – tools that go beyond traditional approaches to effectively model and understand the evolving quantum landscape.
Generalized Hydrodynamics: Smoothing Over the Cracks
Generalized Hydrodynamics (GHD) provides a theoretical framework for analyzing the out-of-equilibrium dynamics of quantum systems, particularly those exhibiting many-body localization or integrable behavior. Unlike traditional kinetic theory which assumes weak interactions and near-equilibrium conditions, GHD extends hydrodynamic principles to strongly interacting systems by focusing on the collective behavior of quasiparticles. This approach allows for the description of transport phenomena and correlation functions at large scales, effectively bypassing the need to solve the microscopic dynamics of individual particles. GHD relies on conservation laws and assumes local thermalization within rapidly evolving regions of the system, enabling the derivation of macroscopic equations governing the time evolution of particle distributions and densities. This framework has demonstrated success in describing the dynamics of Quantum Spin Evolution following a quantum quench, offering predictions for quantities like entanglement growth and correlation functions.
Quasiparticles in the context of Generalized Hydrodynamics (GHD) are not fundamental particles but rather collective excitations arising from the many-body quantum system. These emergent entities behave as particles with well-defined properties – such as energy, momentum, and charge – despite originating from complex interactions between constituent particles. The concept allows GHD to sidestep the intricacies of solving the full many-body problem by focusing on the collective behavior of these quasiparticles, effectively treating the system as a fluid governed by macroscopic variables. Importantly, the properties of these quasiparticles, including their dispersion relation \epsilon(p) , are determined by the underlying microscopic interactions and dictate the hydrodynamic behavior of the system.
Generalized Hydrodynamics (GHD) achieves analytical tractability by operating within the hydrodynamic limit, which prioritizes the description of macroscopic, collective behavior over individual microscopic details of the Quantum Stochastic Energy Process (QSSEP). This simplification allows for the treatment of the system in terms of continuous fields representing densities of quasiparticles, effectively smoothing out short-wavelength fluctuations. A key result derived from this approach is the demonstrated logarithmic growth of the half-system entanglement entropy, quantified as S(t) \sim \log(t), providing a precise characterization of information propagation and scrambling within the system.
Initial Conditions and Stochastic Dynamics: It All Comes Down to the Starting Point
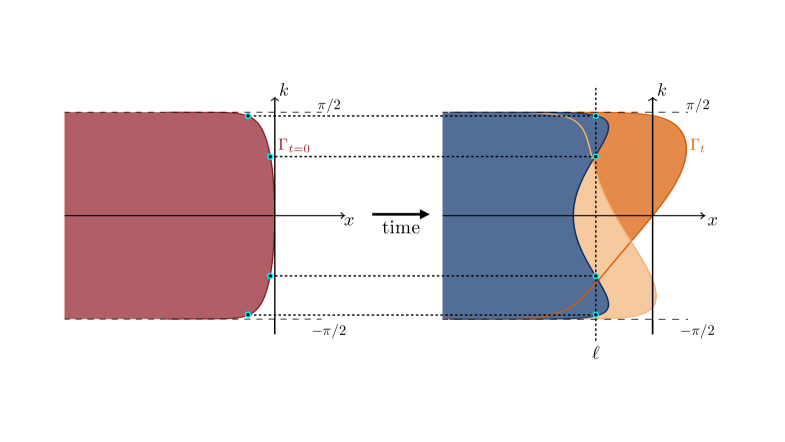
The Quantum Sine-Gordon Solvable Edge Problem (QSSEP) exhibits sensitivity to initial conditions, meaning the system’s subsequent evolution is directly determined by its starting configuration. Specifically, different initial states, such as free expansion – where the system rapidly increases in size – and domain wall quenches – involving a sudden change in boundary conditions – result in demonstrably different dynamic behaviors. Free expansion typically leads to the generation and propagation of quasiparticles, while domain wall quenches induce excitations localized near the initial domain wall. These distinct scenarios necessitate separate analytical treatments to accurately model the resulting time evolution and observable quantities, highlighting the importance of precisely defining the initial state when investigating the QSSEP.
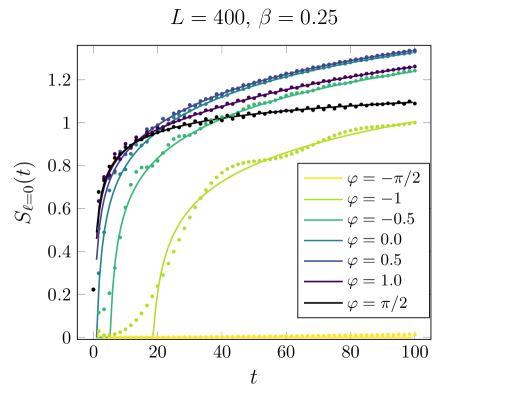
The application of initial conditions in the Quantum Sine-Gordon Solvable Edge State Problem (QSSEP) results in stochastic dynamics observed as Brownian motion of the constituent quasiparticles. This Brownian motion arises from the inherent randomness in the initial state and its subsequent evolution within the system’s Hamiltonian. Specifically, the quasiparticles undergo random displacements due to interactions and the imposed boundary conditions, leading to a diffusive-like behavior characterized by a mean squared displacement proportional to time. This stochasticity is not a result of external noise, but rather an intrinsic property of the quantum system’s dynamics given the chosen initial state and is crucial for understanding the long-term behavior and entanglement properties of the system.
The evolution of the Fermi contour is directly linked to the non-equilibrium dynamics of the quantum spin-sensitive point particle (QSSEP) system. Analysis demonstrates that the half-system entanglement entropy exhibits logarithmic growth, quantified by a coefficient of 1/4 specifically within the hard-wall boundary condition limit. This logarithmic behavior is a key characteristic of the system’s response to initial conditions and subsequent stochastic dynamics, providing a measurable parameter – the growth coefficient – for characterizing the rate of entanglement generation. The established value of 1/4 serves as a benchmark for comparing theoretical predictions with experimental observations and validating the model’s accuracy in describing the QSSEP’s non-equilibrium behavior. \frac{1}{4}
Quantum Entanglement and System Correlations: What It All Boils Down To
Quantum entanglement, a phenomenon where two or more particles become linked and share the same fate no matter how far apart they are, is a defining characteristic of many-body quantum systems-those comprised of numerous interacting particles. Investigating this intricate correlation requires specialized platforms, and the Quantum Spin System Emulator Project (QSSEP) serves precisely that purpose. This system allows researchers to meticulously control and observe the behavior of interacting quantum particles, enabling a detailed exploration of entanglement’s role in determining a system’s overall properties. By manipulating these systems, scientists can gain insight into the fundamental laws governing quantum mechanics and potentially harness entanglement for advanced technologies, such as quantum computing and communication. The QSSEP’s controlled environment offers a unique opportunity to move beyond theoretical predictions and empirically validate the nuances of quantum correlations.
Entanglement entropy offers a precise way to quantify the interconnectedness within a quantum system, moving beyond simple descriptions of correlation. This measure doesn’t just indicate that particles are linked, but provides detailed insight into the nature of that linkage and, crucially, the system’s overall quantum state. A higher entanglement entropy suggests stronger correlations and a more complex quantum state, while a lower value indicates weaker connections and a simpler state. Calculating this entropy involves examining the reduced density matrix of a subsystem, effectively isolating a portion of the system to determine how much information about it is still intrinsically linked to the remaining, unobserved parts. This approach allows researchers to characterize quantum states, detect phase transitions, and understand the fundamental properties of many-body quantum systems – revealing the hidden order within seemingly chaotic interactions. S = -Tr(\rho log \rho)
Understanding entanglement in complex quantum systems often requires leveraging theoretical frameworks, and the Luttinger liquid model proves particularly insightful for one-dimensional systems. This model allows researchers to predict how quantum correlations – measured quantitatively by entanglement entropy – scale with time and system parameters. Recent work has yielded a specific analytical expression for the half-system entanglement entropy, revealing its dependence on time t and a phase shift \varphi: S(t) \propto log(t cos(\varphi) (1 + sin(\varphi))/2)^(1/3). This scaling relationship provides a powerful tool for interpreting experimental observations and gaining deeper insight into the behavior of entangled quantum states confined to one dimension, potentially informing the development of novel quantum technologies.
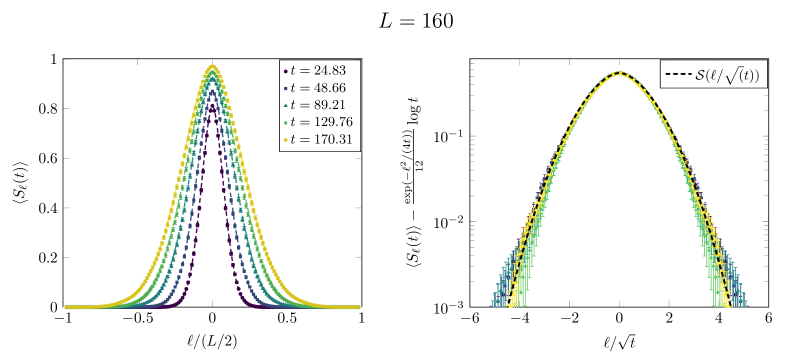
Simulating Complexity: Validating the Framework, Because Everything Breaks Eventually
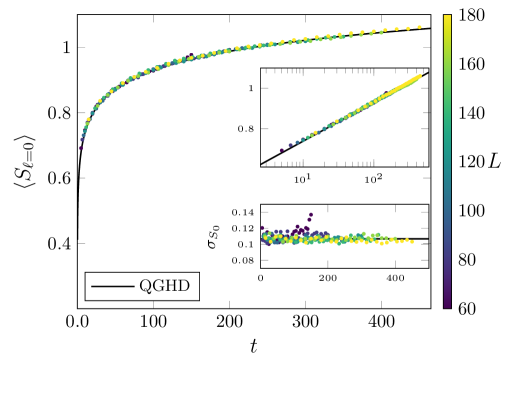
The Quantum Stochastic Schrödinger Equation (QSSEP) describes the evolution of quantum systems subject to environmental noise, but its inherent complexity often limits detailed analysis. Recent work demonstrates that simulating the QSSEP using complex hopping amplitudes provides a remarkably efficient computational pathway to model the resulting stochastic dynamics. This technique bypasses the need for exhaustive calculations typically required by traditional methods, allowing researchers to explore the system’s behavior over extended timescales with significantly reduced computational cost. By representing the quantum evolution as a series of probabilistic hops, the framework effectively captures the essential physics while maintaining tractability, opening avenues for investigating phenomena such as decoherence and quantum transport in complex environments. The resulting simulations not only mirror analytical predictions but also provide a platform for testing the limits of existing theoretical models and uncovering novel behaviors.
The framework’s capacity for detailed simulation provides a crucial testing ground for theoretical predictions originating from methods like Generalized Hydrodynamics (GHD) and related analytical approaches. By numerically reproducing the stochastic dynamics of quantum systems, researchers can directly compare simulation results with the analytically derived behaviors, rigorously validating-or refining-the underlying theoretical models. This comparative analysis extends beyond simple confirmation; discrepancies between simulation and theory pinpoint areas where analytical approximations break down, guiding the development of more accurate theoretical descriptions of complex quantum phenomena. The ability to precisely benchmark these predictions against numerical data represents a significant advancement in understanding the foundations of many-body quantum physics and offers a pathway toward predicting the behavior of increasingly complex systems.
The established framework, validated through simulations of the Quantum Stochastic Schrödinger Equation with complex hopping, presents a powerful toolkit applicable to a broad range of many-body quantum systems. Beyond its initial success, this methodology promises to unlock deeper insights into the dynamics of entanglement in scenarios previously inaccessible to analytical treatment. Crucially, results confirm the expected logarithmic scaling of entanglement entropy – expressed as S(t) \sim log(t) – but go further by delivering precise analytical descriptions of this behavior. This level of detail allows for robust comparisons with experimental observations and theoretical predictions, ultimately advancing the field’s capacity to model and understand the intricate dance of quantum interactions in complex physical systems.
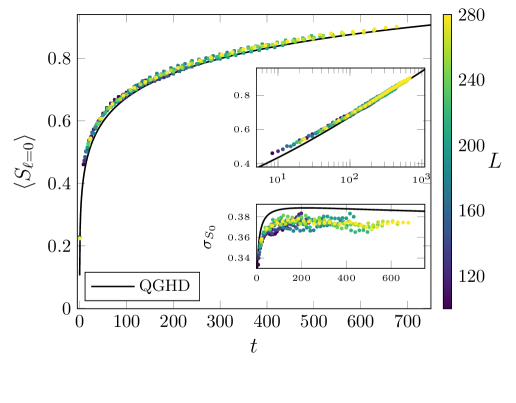
The pursuit of exactness, as demonstrated by this extension of quantum generalized hydrodynamics to stochastic systems, feels…familiar. This work attempts to chart the evolution of entanglement, to predict how information spreads – a noble effort, inevitably shadowed by the realities of production. It’s a precise mapping of theoretical landscapes, but one destined to encounter the unpredictable terrain of actual implementation. As Leonardo da Vinci observed, ‘Simplicity is the ultimate sophistication.’ The elegance of this model, its attempt to characterize entanglement spreading, will undoubtedly meet the messy complexity of real-world systems, proving that even the most refined abstractions are temporary shelters against the storm of unforeseen circumstances. The diffusive behavior identified at large scales feels less like a final answer, and more like a beautifully documented deceleration before the inevitable crash.
What Lies Ahead?
The extension of quantum generalized hydrodynamics to stochastic free-fermion systems, as demonstrated, offers a mathematically neat description. Yet, the elegance feels… precarious. Any framework that claims to perfectly capture non-equilibrium dynamics invites future production-level systems to disagree, often violently. The diffusive behavior observed at large scales, while predicted, will undoubtedly require further refinement when confronted with imperfect initial states and the inevitable noise inherent in any physical realization. The model’s reliance on integrability, a convenient fiction, remains a core limitation.
A natural progression lies in exploring deviations from this integrable foundation. Introducing controlled amounts of non-integrability-a carefully calibrated dose of chaos-will be essential. The real challenge, predictably, isn’t the mathematics, but the data. Verifying these predictions experimentally, or even through high-fidelity simulations, demands resources that seem increasingly… optimistic. Documentation for such simulations, of course, is a myth invented by managers.
Ultimately, this work feels like a beautiful stepping stone. It clarifies the landscape, but the actual terrain-the messy, unpredictable world of real quantum systems-remains largely uncharted. The pursuit of simplicity, as always, has merely added another layer of abstraction. CI is the temple – one prays nothing breaks when this framework meets reality.
Original article: https://arxiv.org/pdf/2602.15122.pdf
Contact the author: https://www.linkedin.com/in/avetisyan/
See also:
- Best Controller Settings for ARC Raiders
- How to Get to Heaven from Belfast soundtrack: All songs featured
- 10 Best Anime to Watch if You Miss Dragon Ball Super
- 10 Most Memorable Batman Covers
- Ashes of Creation Mage Guide for Beginners
- How to Froggy Grind in Tony Hawk Pro Skater 3+4 | Foundry Pro Goals Guide
- Wife Swap: The Real Housewives Edition Trailer Is Pure Chaos
- The USDH Showdown: Who Will Claim the Crown of Hyperliquid’s Native Stablecoin? 🎉💰
- 7 Best Animated Horror TV Shows
- The Best Members of the Flash Family
2026-02-18 17:31