Beyond Gaussianity: Unveiling Order in 2D Superfluids

by

Author: Denis Avetisyan

New matter-wave interferometry experiments reveal the full distribution of order parameter fluctuations in two-dimensional Bose gases, providing insights into universal behavior at the BKT transition and non-equilibrium dynamics.

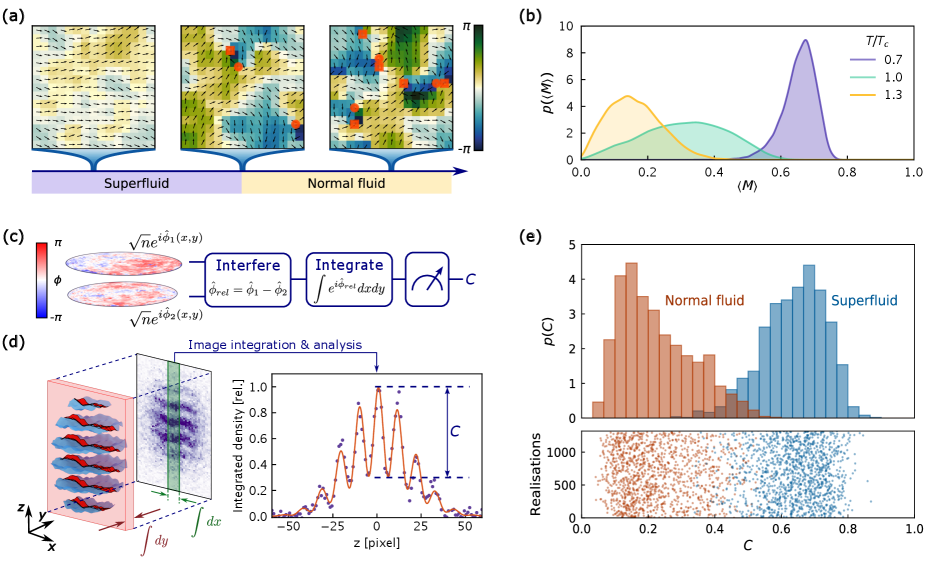
The study demonstrates that the statistical behavior of order parameters in a two-dimensional XY model-a system exhibiting a BKT (Kosterlitz-Thouless) transition-exhibits non-Gaussian features across the critical point, evidenced by matter-wave interferometry which translates relative phase fluctuations of 2D Bose gases into measurable interference patterns, and reveals a proliferation of vortex-antivortex pairs as the system transitions from a quasi-ordered superfluid regime to a normal phase with increased fluctuations.
The study demonstrates that the statistical behavior of order parameters in a two-dimensional XY model-a system exhibiting a BKT (Kosterlitz-Thouless) transition-exhibits non-Gaussian features across the critical point, evidenced by matter-wave interferometry which translates relative phase fluctuations of 2D Bose gases into measurable interference patterns, and reveals a proliferation of vortex-antivortex pairs as the system transitions from a quasi-ordered superfluid regime to a normal phase with increased fluctuations.

Researchers directly measure the non-Gaussian statistics of the order parameter in 2D superfluids, confirming theoretical predictions about the BKT transition and probing dynamics after a sudden quench.

While conventional descriptions of phase transitions often rely on Gaussian fluctuations, many-body systems exhibit rich, non-Gaussian behavior arising from strong correlations and criticality. This is explored in ‘Universal non-Gaussian order parameter statistics in 2D superfluids’, where researchers utilize matter-wave interferometry to probe the full distribution of order parameter fluctuations in two-dimensional Bose gases. Their measurements confirm the convergence of these statistics to a universal Gumbel distribution at low temperatures near the Berezinskii-Kosterlitz-Thouless (BKT) transition, and reveal parameter-independent scaling in non-equilibrium dynamics following a quench. Can these precise measurements of order parameter statistics provide further insights into the fundamental nature of quantum phase transitions and critical phenomena?

Beyond Simple Averages: Unveiling Hidden Order

Conventional descriptions of complex systems, comprised of numerous interacting components, frequently prioritize averaged properties like mean values or standard deviations. While computationally efficient, this approach can obscure crucial information about the system’s underlying statistical behaviour. Many physical phenomena exhibit significant fluctuations around these averages, and the distribution of these fluctuations is often non-Gaussian – deviating substantially from the familiar bell curve. This is particularly relevant near critical points, where subtle changes in control parameters can trigger dramatic shifts in system behaviour, and where these fluctuations aren’t merely noise, but are intrinsic to the emerging order. Ignoring the full distribution of relevant quantities, therefore, risks overlooking key insights into the system’s dynamics and potentially misinterpreting the nature of phase transitions or other collective phenomena. A complete statistical characterization, encompassing the entire probability distribution, is often necessary to accurately capture the richness and complexity of these many-body systems.

Characterizing topological phase transitions, such as the Berezinskii-Kosterlitz-Thouless (BKT) transition, necessitates moving beyond simple averages and embracing a comprehensive statistical framework – the Full Distribution Function (FDF). Unlike methods that focus solely on order parameters or their average values, the FDF provides a complete picture of the probability of finding the system in any given state. This is crucial because these transitions are often accompanied by significant fluctuations and non-Gaussian behaviour, meaning the spread of possible states is as important as the most probable one. By mapping the entire distribution of the order parameter, researchers gain a more nuanced understanding of the system’s response to external stimuli and can accurately pinpoint the critical point where the transition occurs, revealing details obscured by traditional averaging techniques. The FDF, therefore, isn’t merely a descriptive tool, but a necessary component for accurately modeling and predicting the behaviour of complex systems undergoing topological changes.

The BKT transition, prominently demonstrated within the two-dimensional XY model, serves as a crucial example of where conventional mean-field theory falters. This theory, which simplifies complex systems by focusing on average properties, often fails to capture the delicate, nuanced order that emerges near critical points. In the 2D XY model – representing, for instance, a magnetic film with continuous spins – interactions between spins create subtle correlations extending over considerable distances. These long-range correlations, and the associated topological defects like vortices, are entirely missed by mean-field approximations that neglect fluctuations. Consequently, predictions regarding the critical temperature – the point at which the system transitions to a disordered state – and the nature of the order parameter itself become inaccurate, emphasizing the necessity for methods that account for the full range of statistical behaviours beyond simple averages.

Current methodologies often fall short when charting the behaviour of order parameters as a system approaches a critical point, a limitation stemming from their reliance on simplified assumptions about the underlying statistical distributions. These approaches frequently struggle to capture the nuanced fluctuations and correlations that emerge near criticality, leading to inaccurate predictions of system behaviour. Consequently, researchers are actively pursuing innovative techniques – including advanced numerical simulations and analytical methods beyond traditional mean-field theory – to comprehensively map the full distribution function of the order parameter. This deeper understanding is crucial not only for accurately characterizing phase transitions, like the BKT transition, but also for potentially uncovering novel emergent phenomena hidden within these complex systems, demanding a shift from merely knowing if a transition occurs, to fully understanding how it unfolds at a statistical level.

Measurements of skewness, kurtosis, and the Binder cumulant of interference contrast reveal a characteristic step-like change across the BKT critical point, corroborated by both experimental data (purple markers) and Monte Carlo simulations (red lines and open markers), and consistent with critical phase-space density estimates (green and yellow shaded areas) and finite-size scaling predictions.
Measurements of skewness, kurtosis, and the Binder cumulant of interference contrast reveal a characteristic step-like change across the BKT critical point, corroborated by both experimental data (purple markers) and Monte Carlo simulations (red lines and open markers), and consistent with critical phase-space density estimates (green and yellow shaded areas) and finite-size scaling predictions.

Mapping Quantum States: A New Window onto Many-Body Physics

Ultracold atomic gases, typically created using laser and evaporative cooling techniques, offer a highly controllable environment for many-body physics investigations. Achieving temperatures on the order of nanokelvin allows for the observation of quantum effects on a macroscopic scale and minimizes thermal fluctuations. The use of neutral atoms, such as rubidium or sodium, reduces interactions with external electromagnetic fields, enhancing isolation and control. Furthermore, these gases provide access to a large number of particles – often exceeding 10^5 – enabling statistically significant measurements of collective quantum phenomena. Precise control over interatomic interactions, achieved via Feshbach resonances, allows researchers to tune the system’s Hamiltonian and explore a wide range of many-body phases and behaviors.

Matter-wave interferometry leverages the wave-particle duality of matter, specifically ultracold atomic gases, to determine the full distribution function (FDF) of a quantum system. By splitting, propagating, and recombining atomic wavepackets – analogous to light waves in an optical interferometer – interference patterns are generated. The contrast and phase of these interference patterns are directly related to the probability amplitude of finding atoms in different momentum states, thus allowing for a reconstruction of the FDF, which describes the probability distribution of atomic momenta. This technique effectively translates spatial variations in atomic density into measurable interference fringes, providing a direct method for characterizing the momentum distribution without relying on indirect measurements or simplifying assumptions.

The Contrast FDF (Full Distribution Function) Approach utilizes matter-wave interferometry to directly measure the FDF of ultracold atomic gases with enhanced precision. This technique relies on quantifying the contrast of interference patterns formed by splitting, propagating, and recombining atomic wavepackets. Specifically, the visibility of these interference fringes is directly related to the population distribution within the sample; a narrower distribution yields higher contrast. By carefully controlling the splitting and recombination processes, and employing techniques to minimize systematic errors, the Contrast FDF Approach provides a direct, quantitative measurement of the FDF P(k) in momentum space, circumventing the need for indirect inference methods often used in traditional measurements.

Traditional theoretical models of many-body physics, such as the Bose-Hubbard model, often rely on simplifying assumptions to make calculations tractable. While useful for initial understanding, these models may not accurately capture the full complexity of interacting quantum systems. The Contrast FDF approach, utilizing matter-wave interferometry, offers a pathway to circumvent these limitations by directly measuring the full distribution function (FDF) of the atomic gas. This direct observation allows researchers to assess the validity of simplified models and, crucially, to reveal correlations and statistical properties that are masked or entirely absent in those approximations. By characterizing the FDF, the approach provides access to information about many-body effects beyond the mean-field level, enabling a more complete and accurate description of the quantum system’s behavior.

Measurements of the out-of-equilibrium dynamics of a 2D Bose gas following a coherent splitting quench reveal a transition from a superfluid to a normal phase, evidenced by changes in interference contrast and described by a renormalization group flow transitioning through fixed points <span class="katex-eq" data-katex-display="false">x>0, y=0</span>.
Measurements of the out-of-equilibrium dynamics of a 2D Bose gas following a coherent splitting quench reveal a transition from a superfluid to a normal phase, evidenced by changes in interference contrast and described by a renormalization group flow transitioning through fixed points x>0, y=0.

Beyond Gaussianity: Quantifying the Shape of Fluctuations

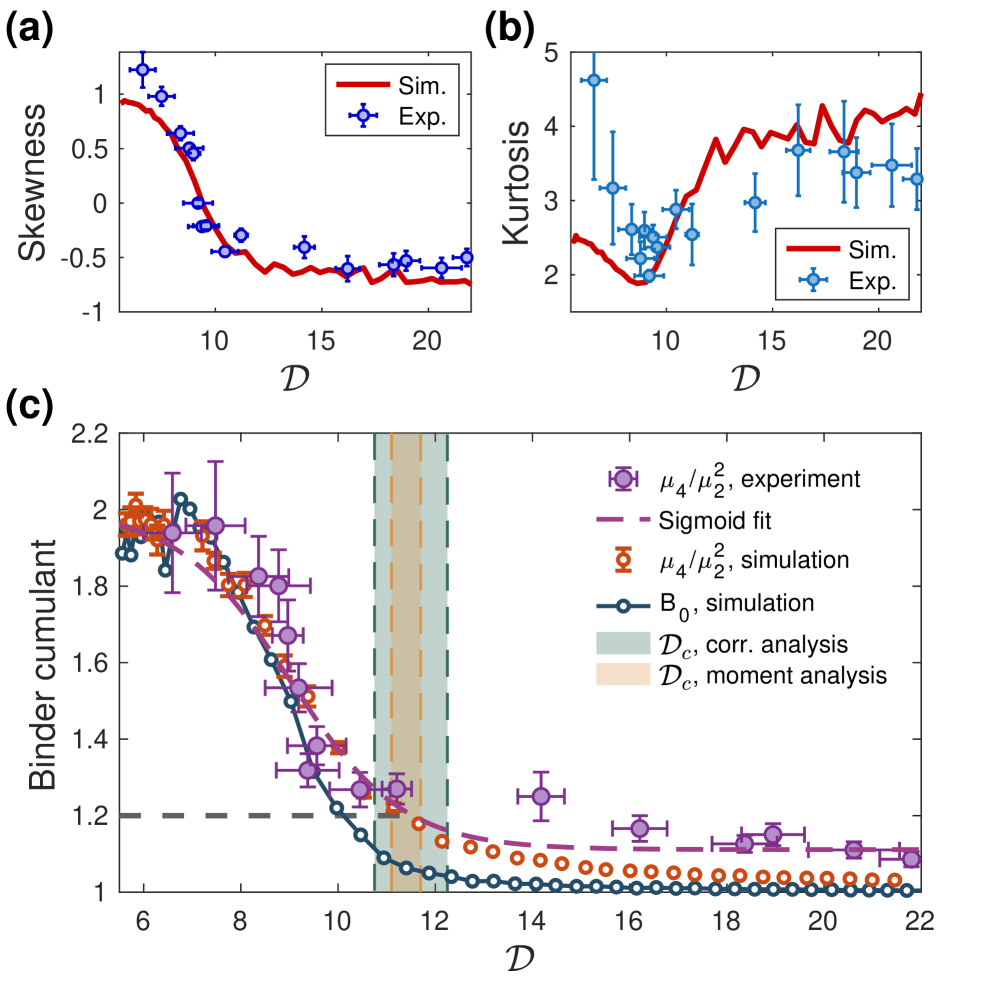
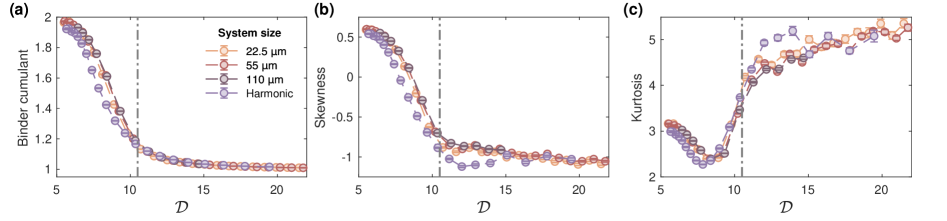
Analysis of the order parameter distribution in the vicinity of the BKT transition demonstrates a significant deviation from Gaussian behavior. Specifically, measurements indicate that the observed distributions are not adequately described by a normal distribution, suggesting the presence of heavier tails and/or asymmetry. This non-Gaussian character is quantified through higher-order statistical moments, such as skewness and kurtosis, which provide a detailed characterization of the distribution’s shape and deviate substantially from the values expected for a Gaussian distribution (skewness = 0, kurtosis = 3). The observed non-Gaussianity is indicative of increased fluctuations and correlations in the order parameter near the transition point, highlighting the limitations of mean-field approaches that assume Gaussian statistics.

Skewness and kurtosis are utilized to quantify deviations from a Gaussian distribution observed in the order parameter’s fluctuations. Skewness, a measure of asymmetry, indicates the degree to which the distribution is skewed to the left or right, while kurtosis describes the “tailedness” of the distribution – specifically, the concentration of probability in the tails versus the center. Analysis reveals a measured skewness bias of 8.5 x 10-3 and a kurtosis bias of -0.045, determined through finite-sampling analysis with N > 1000 samples, with standard deviations of 0.14 and 0.85 respectively. These statistical moments provide detailed information about the shape of the Fluctuations Density Function (FDF), revealing characteristics beyond those described by a simple Gaussian model.

Analysis of the fluctuations in the order parameter within the superfluid phase indicates a distribution consistent with an extreme value distribution, specifically the Gumbel distribution. This finding suggests that large fluctuations, rather than typical values, dominate the behavior of the system near the BKT transition. The Gumbel distribution is characterized by a heavy tail, implying a higher probability of observing extreme events compared to a Gaussian distribution. This is in contrast to systems where fluctuations are well-described by Gaussian statistics, and confirms the non-Gaussian nature of the order parameter distribution observed experimentally.

The observed non-Gaussian behavior of the order parameter distribution near the BKT transition indicates that fluctuations are a primary driver of this phase transition, a phenomenon not adequately described by conventional mean-field treatments which typically assume a homogeneous system. Measurements conducted during this study achieved a critical phase-space density of 11.4 ± 0.3, a value that aligns with results obtained through alternative experimental methodologies. This consistency reinforces the importance of considering fluctuations when modeling the BKT transition and highlights the limitations of approaches that rely solely on averaged quantities.

Finite-sampling analysis, utilizing N > 1000 samples, revealed systematic biases in the measured skewness and kurtosis of the order parameter distribution. The estimated skewness bias was determined to be 8.5 x 10-3, with a standard deviation of 0.14. A kurtosis bias of -0.045 was observed, accompanied by a standard deviation of 0.85. These values quantify the deviation from true statistical moments due to the limitations of finite sample sizes and are crucial for accurate interpretation of the non-Gaussian characteristics near the BKT transition.

Following a quench across the BKT transition in 2D Bose gases, the time evolution of higher-moment observables-skewness, kurtosis, and the Binder cumulant-exhibits universal dynamics when scaled by the crossover time <span class="katex-eq" data-katex-display="false">t_{c}</span>, closely matching equilibrium simulations via the mapping <span class="katex-eq" data-katex-display="false">η ightarrow m_{eq}</span>.
Following a quench across the BKT transition in 2D Bose gases, the time evolution of higher-moment observables-skewness, kurtosis, and the Binder cumulant-exhibits universal dynamics when scaled by the crossover time t_{c}, closely matching equilibrium simulations via the mapping η ightarrow m_{eq}.

Driving the System: Unveiling Dynamics Through Controlled Perturbations

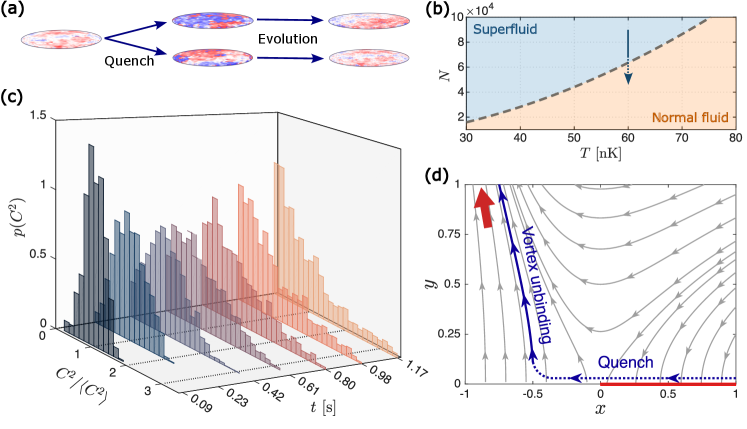
Researchers leverage precisely controlled quenches – abrupt alterations to key system parameters – as a powerful method for investigating the dynamic behavior of complex systems far from equilibrium. By swiftly changing conditions, such as temperature or interaction strength, the system’s initial state is disrupted, initiating a cascade of responses that reveal underlying physical processes. This approach allows scientists to observe how the system evolves over time, tracking the emergence of order, the relaxation towards a new equilibrium, and the propagation of fluctuations. The resulting data provides critical insights into the system’s response to external stimuli and offers a means of validating theoretical models describing non-equilibrium dynamics, furthering understanding of phenomena ranging from condensed matter physics to cosmology.

Researchers leverage a technique called Coherent Splitting to initiate studies of dynamic system behavior. This method involves rapidly dividing a single, ultra-cold gas into two spatially separated and non-interacting clouds. By starting with a single, well-defined quantum state and then partitioning it, scientists establish a highly controlled initial condition for observing how the system evolves away from equilibrium. This precise preparation is crucial, as it allows for detailed comparisons with theoretical predictions and isolates the effects of interactions and external driving forces, offering a unique window into the fundamental physics governing the system’s response.

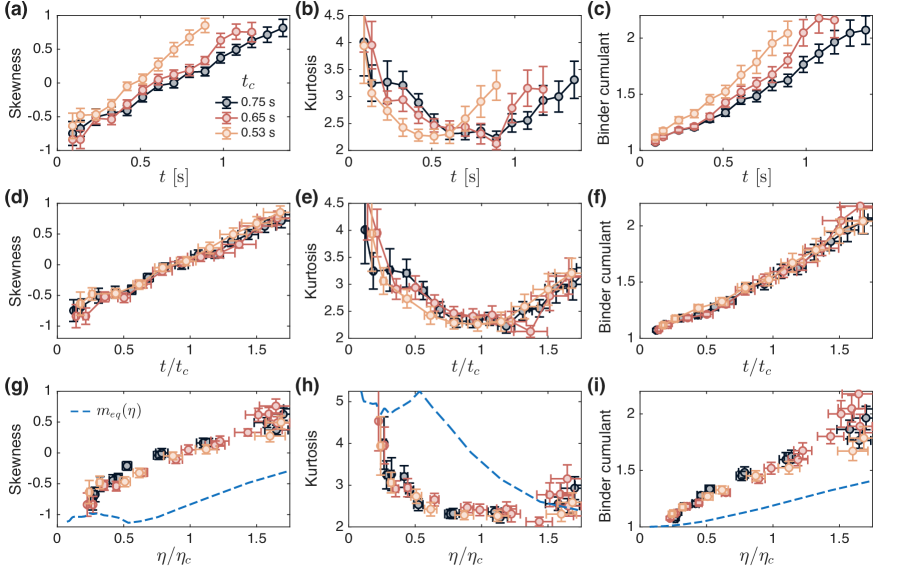
The Real-Time Renormalization Group (RTRG) offers a powerful lens through which to examine the intricate dance of parameters as a system evolves away from equilibrium. Unlike traditional renormalization group methods focused on static properties, RTRG dynamically tracks how effective interactions and relevant scales change over time. This approach doesn’t simply predict a system’s eventual state; it maps the flow of parameters – essentially, how they ‘run’ with time – revealing the underlying mechanisms driving the system’s behavior. By applying RTRG to experiments involving sudden changes – or ‘quenches’ – researchers can dissect the non-equilibrium dynamics, gaining insights into how fluctuations grow, how correlations emerge, and ultimately, how the system navigates towards a new, potentially ordered, state. The framework effectively allows scientists to observe the system’s internal ‘response’ to external stimuli and determine the dominant processes at play, offering a detailed understanding of complex, time-dependent phenomena.

Investigations into driven systems undergoing rapid parameter changes demonstrate a compelling evolution of fluctuations, offering crucial insights into the BKT transition – a hallmark of two-dimensional physics. By observing how these fluctuations respond to varying external forces, researchers can map the dynamic flow of relevant parameters, effectively tracing the system’s path towards or away from the ordered phase. This process illuminates the critical mechanisms at play, revealing how interactions and energy scales shift during the transition and providing a detailed picture of the system’s response to disturbance. Ultimately, understanding this evolution of fluctuations under different driving conditions allows for a deeper comprehension of the BKT transition and the broader principles governing non-equilibrium dynamics.

Analysis of interference contrast statistics from simulations, using up to 150,000 realizations, reveals a critical point-indicated by the grey dashed line-consistent with finite-size scaling observed in Binder cumulant analysis.
Analysis of interference contrast statistics from simulations, using up to 150,000 realizations, reveals a critical point-indicated by the grey dashed line-consistent with finite-size scaling observed in Binder cumulant analysis.

The pursuit of understanding phase transitions, as demonstrated in this study of 2D superfluids, necessitates a rigorous examination of statistical distributions. One must not simply accept initial observations as conclusive. As René Descartes noted, “Doubt is not a pleasant condition, but certainty is absurd.” This research, by mapping the full distribution function of the order parameter, actively embraces that doubt. It moves beyond merely identifying the BKT transition point to characterizing the fluctuations around that point, acknowledging that true understanding arises not from a single measurement, but from a comprehensive assessment of potential deviations. Correlation, indeed, is suspicion, not proof, and this work exemplifies the discipline of uncertainty in its detailed statistical analysis.

Where Does This Leave Us?

The assertion of universality is, of course, a siren song. This work establishes a remarkable degree of consistency in the order parameter statistics of 2D superfluids, even amidst the complexities of non-equilibrium dynamics. However, a precise match to theoretical predictions-particularly regarding critical exponents-remains a subtle game of numerical refinement. One wonders if the observed deviations represent genuine corrections to the established renormalization group framework, or merely the lingering effects of finite-size scaling and imperfect experimental control. The significance level of these discrepancies deserves careful consideration.

Future investigations will likely push beyond equilibrium. Matter-wave interferometry offers a unique lens through which to observe the relaxation dynamics following a quench, but interpreting those observations will require a more nuanced understanding of the interplay between coherence and dissipation. A model isn’t a mirror of reality-it’s a mirror of its maker-and current models may be overly reliant on simplified assumptions about the system’s memory.

Perhaps the most intriguing direction lies in extending these techniques to systems further from the ideal Bose gas. Exploring the impact of interactions beyond the mean-field level, or investigating the behavior of more complex condensates, could reveal previously hidden facets of the BKT transition. A truly universal understanding, if attainable, will likely emerge not from confirming expectations, but from systematically dismantling them.

Original article: https://arxiv.org/pdf/2601.16204.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/

See also:

2026-01-23 15:15