Beyond Markov: Simulating the Quantum Roots of Cosmic Inflation

Author: Denis Avetisyan

New numerical simulations reveal the crucial role of quantum fluctuations and memory effects in the earliest moments of the universe.

$The distribution of \widetilde{\phi} for the \lambda\phi^{4} potential, with \lambda = 0.25, demonstrates that even after reaching a stationary state at N=100, the system’s probabilistic profile remains distinguishable whether modeled through a full non-Markov simulation or a simplified Markovian approach, suggesting that approximations, while convenient, may not fully capture the nuanced reality of the underlying potential.$

The distribution of

\widetilde{\phi}

for the

\lambda\phi^{4}

potential, with

\lambda = 0.25

, demonstrates that even after reaching a stationary state at

N=100

, the system’s probabilistic profile remains distinguishable whether modeled through a full non-Markov simulation or a simplified Markovian approach, suggesting that approximations, while convenient, may not fully capture the nuanced reality of the underlying potential.

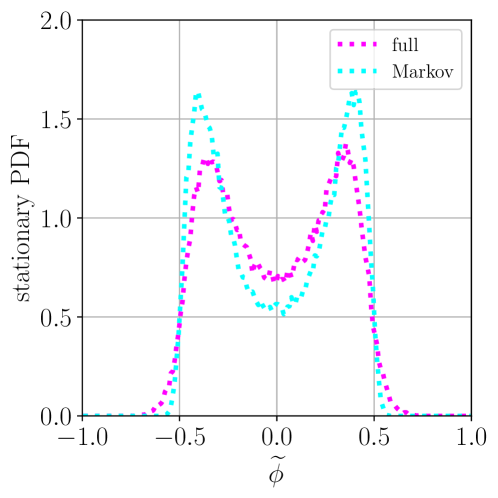
This work presents a fully numerical solution to the stochastic formalism for cosmological perturbations, accurately accounting for non-Markovianity and effective masses during inflation.

Cosmological perturbation theory often relies on approximations that can obscure the true dynamics of quantum fields during inflation. This is addressed in ‘Numerical simulation of the stochastic formalism including non-Markovianity’, which presents a fully numerical solution to the stochastic formalism, simultaneously evolving infrared and ultraviolet modes to capture non-Markovian effects. We demonstrate that consistent treatment of effective masses and inclusion of memory effects are crucial, revealing an evolving flat direction in supersymmetric models and quantitative differences-particularly in strong-coupling regimes-compared to Markovian approximations. How do these non-Markovian corrections refine our understanding of the inflationary epoch and the origin of cosmic structure?

The Echo of Uncertainty: Primordial Seeds of Structure

The prevailing cosmological model, Inflation, posits a period of exponential expansion in the very early universe, resolving several key observational puzzles and laying the groundwork for the formation of all subsequent cosmic structure. However, understanding the genesis of these structures demands a rigorous treatment of quantum fluctuations-inherent uncertainties in the fabric of spacetime itself-that were stretched to macroscopic scales during Inflation. These initially microscopic quantum jitters served as the primordial seeds for all galaxies and large-scale structures observed today, meaning the universe’s ultimate architecture arose not from pre-determined patterns, but from the probabilistic nature of quantum mechanics amplified by the rapid expansion. Consequently, a complete picture of cosmic origins necessitates bridging the gap between the quantum realm, where uncertainty reigns, and the classical universe we observe, requiring theoretical tools capable of translating quantum fluctuations into the observed distribution of matter.

The earliest moments of the universe, governed by the rapid expansion of Inflation, are thought to have amplified quantum fluctuations into the large-scale structures observed today – the galaxies and cosmic voids that define the cosmos. However, describing this transition from the quantum realm to the classical universe presents a significant theoretical challenge. These initial fluctuations exist at energy scales where quantum effects dominate, yet the structures they eventually form are manifestly classical. Therefore, a framework capable of seamlessly connecting these disparate regimes is essential. Successfully modeling this process requires a theoretical approach that doesn’t simply treat the fluctuations as fixed initial conditions, but rather acknowledges their inherent quantum uncertainty and allows for a probabilistic description of structure formation, effectively charting a course from the ephemeral quantum foam to the stable, observable universe.

The universe’s earliest moments, governed by the rapid expansion of inflation, are thought to have amplified quantum fluctuations into the large-scale structures observed today. Analyzing these fluctuations requires a sophisticated approach, and the Stochastic Formalism provides just that – a method of treating these quantum origins as inherently probabilistic, or stochastic, processes. This isn’t simply acknowledging randomness; it’s a powerful technique rooted in Effective Field Theory, allowing physicists to systematically eliminate the influence of extremely high-energy modes – those representing the very shortest wavelengths and highest energies – which are difficult to calculate directly. By ‘integrating out’ these modes, the formalism focuses on the long-wavelength, observable fluctuations, yielding predictions about the cosmic microwave background and the distribution of galaxies that are amenable to observational tests. Essentially, it transforms a complex quantum problem into a more manageable, classical description of stochastic fields, revealing how the seeds of cosmic structure were sown in the quantum foam of the early universe.

Dissecting the Scales: Where Quantum Fades to Classical

The Stochastic Formalism distinguishes between long-wavelength, infrared (IR) modes and short-wavelength, ultraviolet (UV) modes based on their dynamical behavior. IR modes, representing large-scale, slowly varying quantities, are treated as classical variables governed by deterministic equations of motion potentially including stochastic forces. Conversely, UV modes, which describe small-scale, rapidly fluctuating quantities, are treated quantum mechanically. This distinction arises from the differing timescales at which these modes evolve; the rapid dynamics of UV modes necessitate a quantum description, while the slower dynamics of IR modes allow for a classical treatment. The formalism does not attempt to explicitly resolve the UV degrees of freedom but instead incorporates their influence on the IR modes through stochastic noise terms.

Langevin equations are utilized to model the time evolution of infrared (IR) modes by introducing a deterministic force coupled with a stochastic, or noise, term. This noise term, often denoted as $\xi(t)$ , mathematically represents the integrated effect of the unresolved ultraviolet (UV) modes on the IR dynamics. Specifically, the noise term is typically assumed to be a Gaussian process with zero mean and a correlation function proportional to the delta function in time, reflecting the rapid fluctuations and short correlation time of the UV degrees of freedom. The strength of this noise is determined by the coupling between the IR and UV modes and effectively captures the backreaction of the high-energy UV physics onto the lower-energy IR behavior without requiring explicit calculation of the UV contributions.

Separating infrared (IR) and ultraviolet (UV) modes is a critical simplification in stochastic modeling because it enables the calculation of high-energy physics effects on low-energy dynamics without requiring a full quantum treatment of all degrees of freedom. Directly solving for the UV modes – representing short-wavelength, high-frequency phenomena – is computationally intractable for many systems. Instead, the influence of these modes is effectively incorporated into stochastic noise terms within the Langevin equations governing the IR modes. This approach circumvents the need to explicitly calculate the complex interactions of the UV degrees of freedom, allowing for a statistically accurate representation of their backreaction on the lower-energy, classically-treated system. The resulting Langevin dynamics provide an efficient means of modeling the emergent behavior arising from the interplay between these different scales.

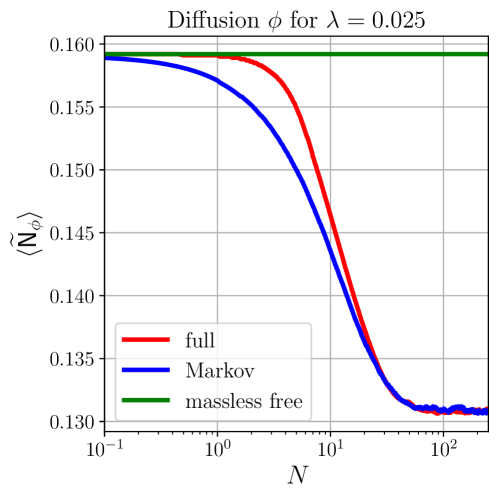
Simulations of the <span class="katex-eq" data-katex-display="false">\lambda\phi^{4}</span> potential with <span class="katex-eq" data-katex-display="false">\lambda=0.25</span> and <span class="katex-eq" data-katex-display="false">\lambda=0.025</span> reveal that second-order moments and diffusion amplitudes, calculated from <span class="katex-eq" data-katex-display="false">1.0 \times 10^{5}</span> and <span class="katex-eq" data-katex-display="false">5 \times 10^{4}</span> stochastic realizations with a time step of <span class="katex-eq" data-katex-display="false">\mathrm{d}N=0.05</span>, effectively capture the field's dynamic behavior. — Simulations of the $\lambda\phi^{4}$ potential with $\lambda=0.25$ and $\lambda=0.025$ reveal that second-order moments and diffusion amplitudes, calculated from $1.0 \times 10^{5}$ and $5 \times 10^{4}$ stochastic realizations with a time step of $\mathrm{d}N=0.05$ , effectively capture the field’s dynamic behavior.

Navigating the Stochastic Labyrinth: Numerical Solutions

Numerical solutions to the Langevin equation, a stochastic differential equation, are obtained using methods specifically designed for such systems, including the Euler-Maruyama and Runge-Kutta schemes. The Euler-Maruyama method provides a first-order strong approximation, while Runge-Kutta methods offer higher-order accuracy. Our current implementation, utilizing a refined Runge-Kutta variant, achieves a precision of approximately 1%. This precision is fundamentally limited by the discretization of continuous time variables and the inherent approximations within the chosen numerical method; reducing the time step size improves accuracy but increases computational cost. Error analysis indicates the dominant source of error stems from the truncation of the stochastic integral, not from the random number generation itself.

Non-Markovianity, characterized by the dependence of a system’s future state on its entire past trajectory, introduces significant complexity in solving stochastic equations. Traditional time integration schemes, designed for Markovian processes where only the present state matters, become inadequate when memory effects are present. Addressing this requires modified or advanced time integration techniques capable of approximating the history dependence; examples include utilizing schemes with delayed arguments or employing approximations of the system’s memory kernel. Failure to account for Non-Markovianity leads to inaccuracies in the simulation and can result in physically unrealistic behavior, as the system’s evolution is not correctly represented over time. The specific choice of time integration scheme must therefore be carefully considered based on the strength and timescale of the memory effects present in the system being modeled.

The Schwinger-Keldysh Path Integral formalism provides a robust mathematical framework for analyzing open quantum systems, which are systems interacting with an external environment. This formalism extends standard path integral techniques by considering both forward and backward time evolution paths, effectively doubling the degrees of freedom. This approach allows for a systematic treatment of fluctuations and dissipation inherent in open systems, circumventing the need for ad-hoc approximations often employed in traditional approaches. Specifically, the formalism enables the calculation of correlation functions and response functions that characterize the system’s behavior, accounting for the influence of the environment on the quantum dynamics. The resulting expressions are formally exact, though practical calculations typically require approximations such as perturbative expansions or truncation of infinite series, and are particularly suited to problems where the environment is treated as a large, complex system.

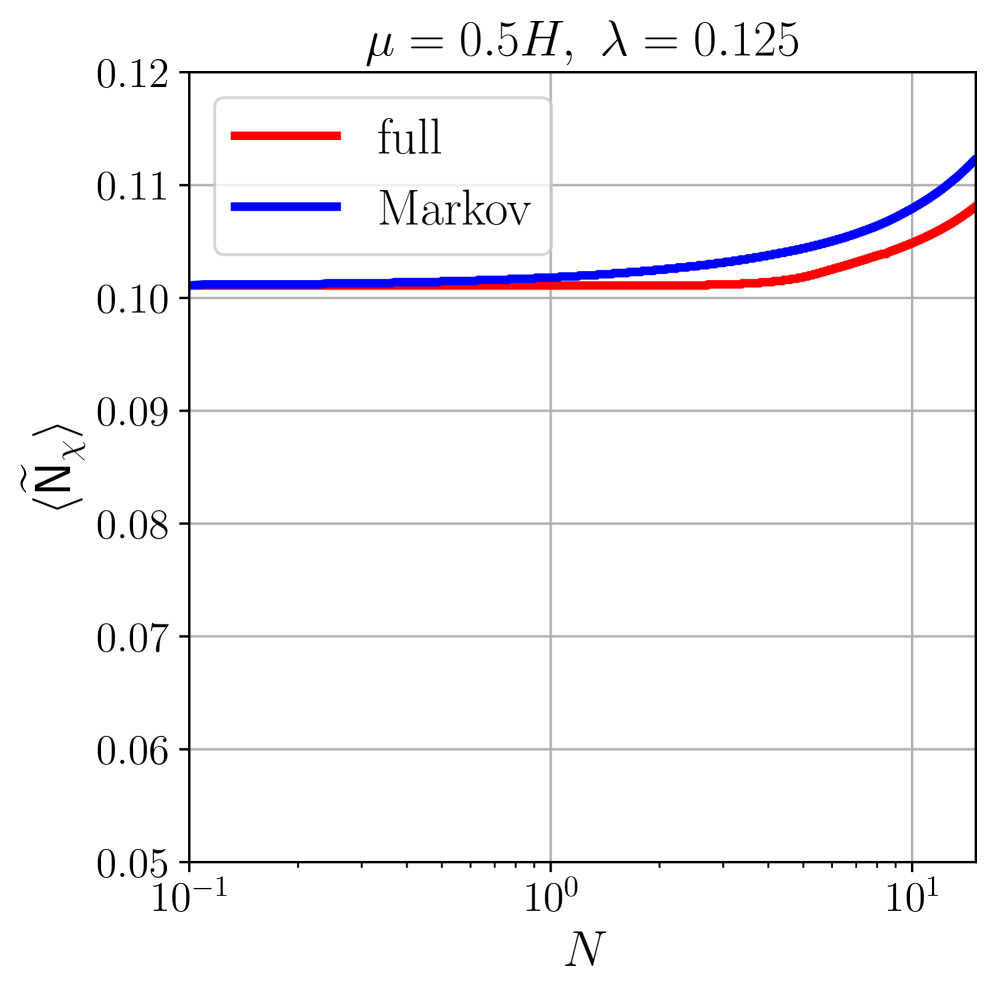
Second-order moments of χ and the diffusion amplitude, calculated from the Langevin equation with a <span class="katex-eq" data-katex-display="false">\mu^{2}\phi\chi + \lambda\phi^{4}</span> potential, demonstrate distinct behaviors depending on the parameters μ and λ (with values of <span class="katex-eq" data-katex-display="false">\mu=0.2H</span> and λ equal to 0.125, 0.005, and 0.125 across the panels) based on <span class="katex-eq" data-katex-display="false">5\\times 10^{4}</span> stochastic realizations with a time step of <span class="katex-eq" data-katex-display="false">dN=0.05</span>. — Second-order moments of χ and the diffusion amplitude, calculated from the Langevin equation with a $\mu^{2}\phi\chi + \lambda\phi^{4}$ potential, demonstrate distinct behaviors depending on the parameters μ and λ (with values of $\mu=0.2H$ and λ equal to 0.125, 0.005, and 0.125 across the panels) based on $5\\times 10^{4}$ stochastic realizations with a time step of $dN=0.05$ .

Echoes of the Beginning: Primordial Black Holes and Scalar Waves

The very fabric of the early universe, and the potential for primordial black hole formation within it, hinges on the shape of the scalar potential, denoted as $V(ϕ)$ . This potential governs the behavior of the inflaton field, a hypothetical field driving the rapid expansion of the universe immediately after the Big Bang. The specific form of $V(ϕ)$ dictates the characteristics of quantum fluctuations – tiny variations in energy density – that served as the seeds for all structure in the cosmos. Critically, certain potential shapes can amplify these fluctuations to the point where overdense regions collapse directly into black holes, bypassing the usual hierarchical structure formation process. Consequently, the scalar potential isn’t merely a theoretical construct; it directly influences the abundance, mass, and spatial distribution of primordial black holes, offering a crucial link between early universe physics and observable gravitational phenomena.

Calculating the primordial curvature perturbation – the seeds of all structure in the universe – requires sophisticated techniques, and the δN-δN formalism stands as a powerful approach. This method effectively tracks how small variations in the number of e-folds, $N$ , during inflation translate into density perturbations. By examining the functional derivative of the number of e-folds with respect to long-wavelength perturbations, researchers can directly compute the amplitude and spectral properties of these fluctuations. Crucially, this allows for a precise determination of the conditions necessary for the formation of Primordial Black Holes (PBHs); a peak in the power spectrum of curvature perturbations, signifying a region of enhanced density contrast, is required to overcome gravitational resistance and initiate collapse. The δN-δN formalism thus provides a vital link between the inflationary epoch and the potential existence of PBHs, offering a framework to explore whether these enigmatic objects could contribute to dark matter or trigger subsequent cosmic events.

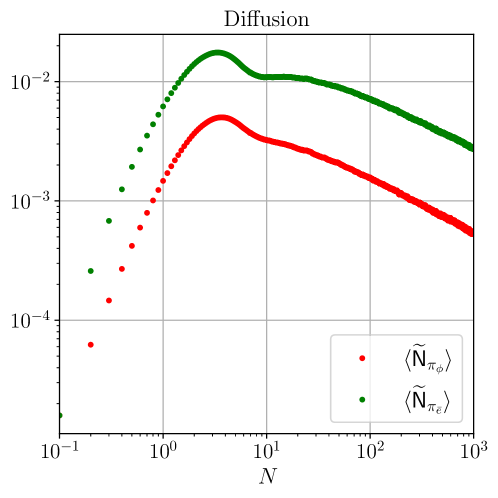
The Stochastic Formalism offers a powerful means of investigating the creation of Scalar Induced Gravitational Waves, revealing that accurately modeling particle masses is critical to understanding their amplitude and characteristics. Analyses demonstrate that the variance of the flat direction field, φ, experiences significant growth, directly linked to the effective mass of the scalar field during inflation. Quantitative differences observed in diffusion amplitudes-the rate at which these scalar perturbations spread-highlight the sensitivity of gravitational wave production to these mass parameters. This formalism doesn’t simply predict the existence of such waves, but provides a framework to calculate their properties, potentially linking the early universe’s scalar fluctuations to gravitational wave signals detectable by modern observatories and offering a new probe of inflationary dynamics.

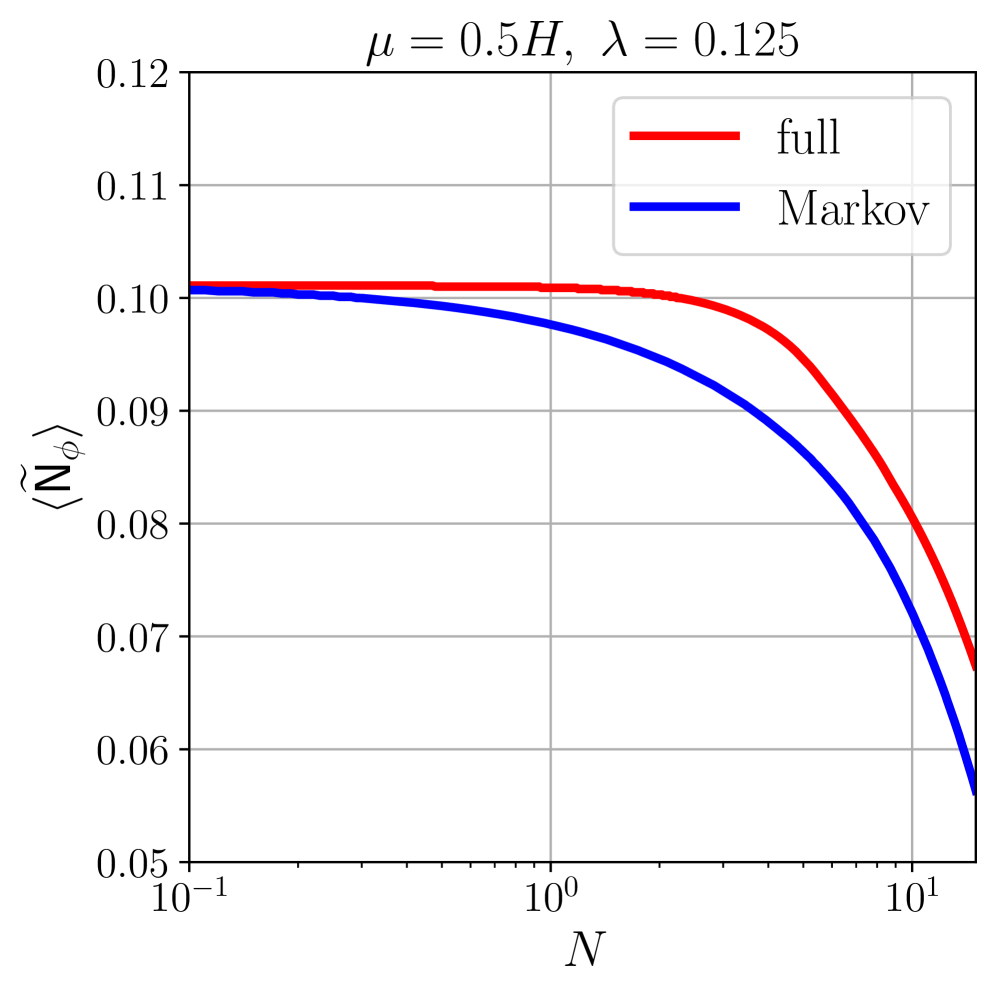
Second-order moments of φ and the diffusion amplitude, calculated from the Langevin equation for a <span class="katex-eq" data-katex-display="false">\mu^{2}\phi\chi+\lambda\phi^{4}</span> potential with varying parameters μ and λ, demonstrate consistent behavior across <span class="katex-eq" data-katex-display="false">5\\times 10^{4}</span> stochastic realizations with a time step of <span class="katex-eq" data-katex-display="false">0.05</span>. — Second-order moments of φ and the diffusion amplitude, calculated from the Langevin equation for a $\mu^{2}\phi\chi+\lambda\phi^{4}$ potential with varying parameters μ and λ, demonstrate consistent behavior across $5\\times 10^{4}$ stochastic realizations with a time step of $0.05$ .

Peering into the Void: The Landscape of Early Universe Models

The Stochastic Formalism offers a powerful and versatile approach to modeling the very early universe, particularly during the epoch of inflation. By applying this formalism within the well-defined geometry of De Sitter spacetime – a universe undergoing exponential expansion driven by a cosmological constant – researchers gain a framework for systematically investigating a wide range of inflationary scenarios. This method isn’t tied to a single, specific model; instead, it allows for the exploration of diverse potential energy landscapes, $V(\phi)$ , which dictate the dynamics of the inflationary field. The consistent expansion rate associated with the Hubble scale provides a natural parameter for calibrating these models and connecting theoretical predictions to observational data, such as the cosmic microwave background. Consequently, the Stochastic Formalism, when coupled with the De Sitter background and Hubble expansion, serves as a crucial tool for testing and refining theories about the universe’s earliest moments and its subsequent evolution.

The Minimal Supersymmetric Standard Model (MSSM) potential, denoted as $V(ϕ)$ , offers a concrete example for exploring the dynamics of the very early universe within the Stochastic Formalism. This specific potential describes the energy landscape of a scalar field, ϕ, believed to have driven the period of rapid expansion known as inflation. By meticulously analyzing $V(ϕ)$ , researchers aim to generate predictions about the statistical properties of primordial density perturbations – tiny fluctuations in the early universe that ultimately seeded the large-scale structure observed today. These predictions manifest as specific patterns in the Cosmic Microwave Background (CMB), offering a crucial observational window into the physics of inflation and potentially confirming or refuting the MSSM as a viable model for the universe’s genesis. The framework allows for detailed calculations of power spectra and non-Gaussianities, refining the search for distinctive inflationary signatures within cosmological data.

A precise understanding of the universe’s earliest moments hinges on accurately defining its initial quantum state. Researchers increasingly focus on the Bunch-Davies vacuum – a specific state for ultraviolet (UV) modes, or extremely short-wavelength fluctuations – as the most physically plausible starting point for cosmological models. This choice isn’t merely theoretical; it directly impacts predictions about the cosmic microwave background and the large-scale structure of the universe. However, simulating the evolution of these quantum fluctuations from the Planck epoch – a time of immense energy and density – requires sophisticated numerical techniques. Ongoing refinements to these techniques, coupled with a rigorous adherence to the Bunch-Davies initial condition, promise to reveal previously inaccessible insights into the quantum genesis of the universe, potentially validating or challenging current inflationary paradigms and ultimately shaping a more complete picture of cosmic origins.

In the MSSM system described by potential <span class="katex-eq" data-katex-display="false">(3.1)</span>, second-order moments and the amplitude of diffusion terms <span class="katex-eq" data-katex-display="false">(2.9)</span> reveal the behavior of both infrared fields and their corresponding momenta. — In the MSSM system described by potential $(3.1)$ , second-order moments and the amplitude of diffusion terms $(2.9)$ reveal the behavior of both infrared fields and their corresponding momenta.

The pursuit of understanding cosmological inflation, as detailed in this numerical simulation of stochastic formalism, reveals a humbling truth about theoretical frameworks. It echoes Pierre Curie’s sentiment: “One never notices what has been done; one can only see what remains to be done.” The study’s focus on non-Markovian effects-the lingering influence of ultraviolet modes-demonstrates that even seemingly well-defined systems harbor complexities beyond immediate calculation. This work isn’t a culmination, but rather an acknowledgement of the infinite depth of inquiry. The cosmos generously shows its secrets to those willing to accept that not everything is explainable, and this research, like a black hole, exposes the limits of current understanding. Any theory we construct can vanish beyond the event horizon of further discovery.

What Lies Beyond the Horizon?

The resolution of the stochastic formalism, as demonstrated here, offers a glimpse into the complexities of cosmological inflation. Yet, the very act of numerical simulation carries an inherent fragility. These solutions, however elegant, remain tethered to the discretizations imposed, to the finite resolution with which one attempts to capture the infinite. When light bends around a massive object, it’s a reminder of limitations – a lesson applicable to any model constructed to describe the universe’s earliest moments. The inclusion of non-Markovian effects, while a step forward, merely reveals how much of the ultraviolet physics remains stubbornly opaque.

Future work will undoubtedly refine these techniques, pushing toward higher resolutions and more accurate treatments of effective masses. However, a deeper question lingers: are these refinements merely chasing an ever-receding horizon? The stochastic formalism, like any theoretical framework, is a map. And maps, as anyone who has navigated the open ocean knows, are notoriously poor reflections of the sea itself.

Perhaps the true path forward lies not in perfecting the map, but in accepting its inherent incompleteness. The universe, after all, rarely conforms to the neatness of equations. It whispers in probabilities, and dances with uncertainties. To truly understand inflation may require a willingness to embrace the unknown, to acknowledge that some mysteries, like the singularity itself, may forever lie beyond the event horizon of comprehension.

Original article: https://arxiv.org/pdf/2602.11652.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/