Beyond Order: Unveiling Hidden Quantum Structure

Author: Denis Avetisyan

A new framework leveraging quantum hyperuniformity reveals previously obscured phases and transitions in quantum systems by characterizing the suppression of long-range fluctuations.

The Aubry-André model exhibits a complex phase diagram characterized by hyperuniformity classes, revealing scaling behaviors of <span class="katex-eq" data-katex-display="false">SQS_Q</span> that depend on both the parameter λ and the Fermi level’s position relative to the band edges-with scaling exponents of 1, 0.618, and 2 for Fermi levels crossing bands at λ = 1, 2, and 3, respectively-and a nuanced landscape of the scaling exponent ν that diversifies significantly at λ = 2, all within a system size of N = 17711. — The Aubry-André model exhibits a complex phase diagram characterized by hyperuniformity classes, revealing scaling behaviors of $SQS_Q$ that depend on both the parameter λ and the Fermi level’s position relative to the band edges-with scaling exponents of 1, 0.618, and 2 for Fermi levels crossing bands at λ = 1, 2, and 3, respectively-and a nuanced landscape of the scaling exponent ν that diversifies significantly at λ = 2, all within a system size of N = 17711.

This review explores quantum hyperuniformity as a probe for identifying critical states and gapless phases, with specific application to quasiperiodic systems like the Aubry-André model.

Identifying and characterizing quantum phases often requires navigating the complexities of many-body interactions and emergent behavior. This is addressed in ‘Quantum Hyperuniformity and Quantum Weight’, which introduces a framework leveraging the suppression of long-wavelength quantum fluctuations-quantum hyperuniformity-to reveal distinct quantum phases and transitions. The study demonstrates that these phases, exemplified in the Aubry-André model, exhibit unique scaling behaviors detectable through the charge-density structure factor and quantified by a ‘quantum weight’ that directly relates to gap size. Could this novel approach offer a practical, universal fingerprint for probing quantum criticality in aperiodic systems and beyond?

The Allure of Hidden Order: Unveiling Many-Body Localization

Contrary to expectations in many areas of physics, quantum systems riddled with disorder don’t always spread out; instead, they can undergo a transition to a localized state. This phenomenon, known as many-body localization, sees the quantum wavefunctions – which describe the probability of finding a particle – become effectively trapped within specific regions of the system. Unlike conventional localization arising from strong, static potentials, this localization emerges from the collective effects of disorder and quantum interactions. The implications are profound, as localized systems resist heating and can retain quantum coherence for extended periods – a crucial attribute for potential quantum technologies. This challenges established understandings of thermalization and opens avenues for exploring fundamentally new phases of matter where interactions prevent the usual spread of quantum information, creating a landscape where $\hbar$ itself dictates an unusual stability.

The ability to predict and control the transitions into many-body localization (MBL) holds significant promise for materials science and fundamental physics research. A deeper comprehension of these transitions allows for the potential design of novel quantum materials with tailored properties; materials that might otherwise be unstable or quickly lose quantum coherence could be stabilized through engineered disorder. Beyond materials, studying MBL provides a unique window into the ergodic versus non-ergodic phases of quantum systems, challenging conventional understandings of thermalization and equilibration. This research area isn’t simply about finding localized states, but rather about understanding how systems avoid heating up and losing quantum information – a critical factor in the development of robust quantum technologies and a powerful tool for probing the foundations of statistical mechanics, potentially revealing entirely new phases of matter governed by previously unknown principles.

Characterizing many-body localization presents a significant challenge to conventional condensed matter physics techniques. Established theoretical approaches, such as mean-field theory and perturbative expansions, often falter when confronted with the strong interactions and substantial disorder inherent in these systems. These methods typically rely on assumptions of translational symmetry or weak interactions, which break down in the highly disordered regime. Numerical simulations, while powerful, are hampered by the exponentially growing Hilbert space associated with many-body quantum systems, limiting the size and timescale of accessible simulations. Consequently, a complete understanding of the interplay between disorder and quantum effects – how these factors collectively dictate the system’s behavior and the precise nature of the localization transition – remains elusive, necessitating the development of novel theoretical frameworks and computational strategies.

The probability distributions of momentum-space wavefunctions for adjacent critical states in the Aubry-André model at <span class="katex-eq" data-katex-display="false">\lambda = 2t</span> reveal distinct patterns based on eigenenergy index <span class="katex-eq" data-katex-display="false">n</span>. — The probability distributions of momentum-space wavefunctions for adjacent critical states in the Aubry-André model at $\lambda = 2t$ reveal distinct patterns based on eigenenergy index $n$ .

Beyond Symmetry: A New Language of Order

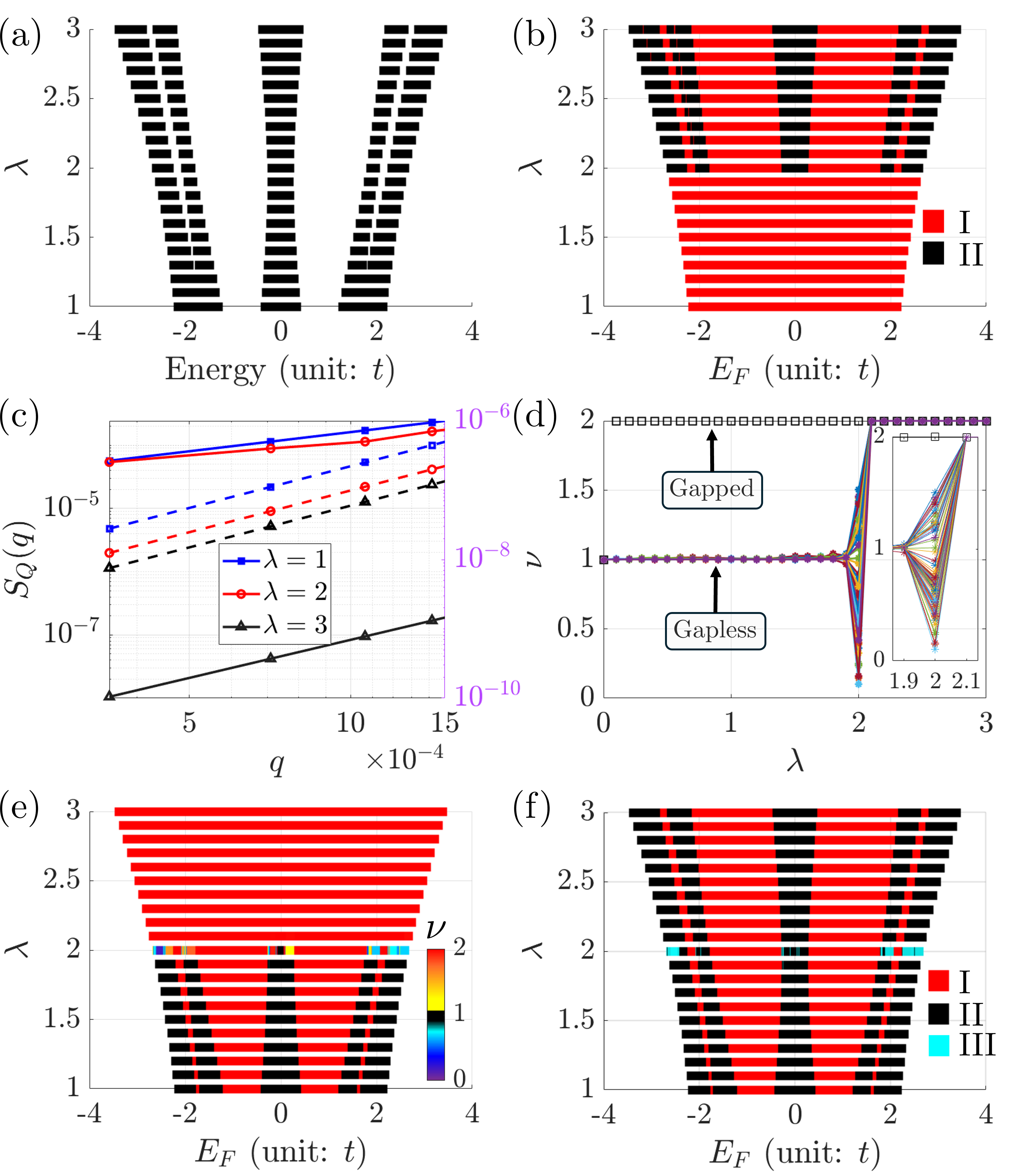
Quantum hyperuniformity (QHU) represents a departure from conventional notions of order based on translational symmetry, as found in crystals. Traditional order relies on repeating patterns across space; QHU, however, defines order through the suppression of density fluctuations at all length scales. This suppression is mathematically characterized by a structure factor, $S(k)$ , which approaches zero as the wavevector $k$ tends to zero, indicating a lack of long-range density correlations. Critically, QHU does not require any symmetry; disordered systems, such as those exhibiting localization, can still exhibit QHU if density fluctuations are sufficiently suppressed, allowing for the detection of hidden order in systems where traditional symmetry-based analysis would fail. This makes QHU a versatile tool for analyzing a broad range of physical systems, extending beyond the realm of crystalline materials.

Quantum hyperuniformity (QHU) is characterized by the suppression of density fluctuations at all length scales, deviating from the expected fluctuations in disordered systems. This suppression is mathematically quantified using the Charge Density Structure Factor, $S(q)$ , where $q$ represents the wavevector. A system exhibiting QHU demonstrates $S(q) \rightarrow 0$ as $q \rightarrow 0$ , indicating a lack of long-range density correlations. Importantly, QHU does not require periodicity; systems can be hyperuniform without possessing Bragg peaks, distinguishing it from conventional crystalline order. The magnitude of $S(q)$ directly relates to the compressibility of the system, with hyperuniform systems exhibiting reduced compressibility due to the suppressed fluctuations.

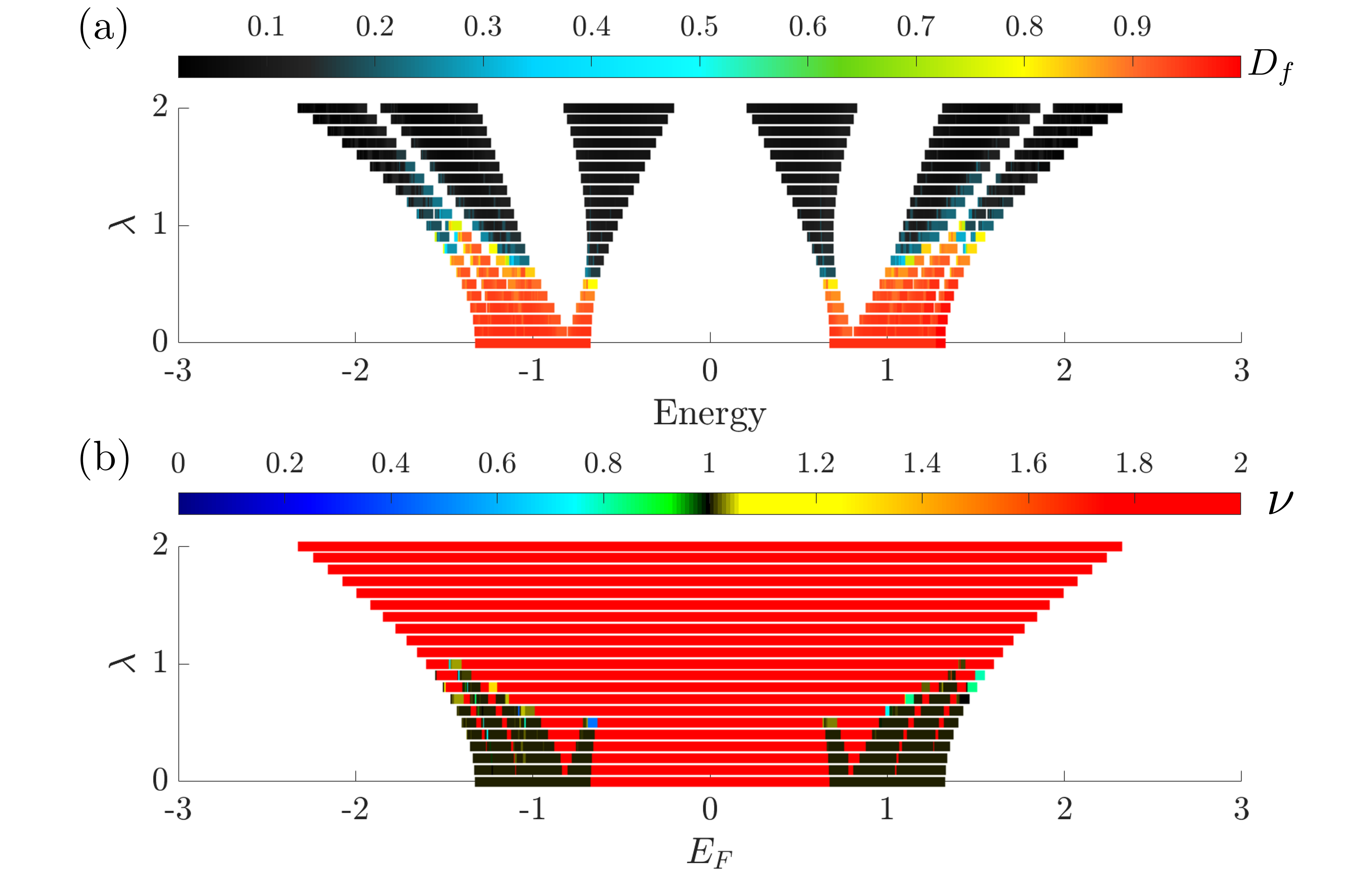
The Aubry-André model, a one-dimensional tight-binding model with a quasi-random potential described by $V_n = \lambda \cos(2\pi \beta n)$ , provides a well-defined system for studying the relationship between quantum hyperuniformity and the localization transition. This model exhibits a transition from extended states to localized states as the potential strength, λ, increases. Critically, studies have shown that quantum hyperuniformity, evidenced by a suppressed density structure factor at large wavelengths, emerges precisely at the localization transition point. The parameter β, representing the incommensurate modulation of the potential, plays a key role in determining the characteristics of this hyperuniform state, and variations in β can tune the degree of hyperuniformity observed. This allows researchers to empirically link the mathematical properties of hyperuniformity to the physical process of Anderson localization.

Phase diagrams for the Aubry-André model at system size <span class="katex-eq" data-katex-display="false">N=17711</span> and time <span class="katex-eq" data-katex-display="false">t=1</span> reveal distinct hyperuniformity classes for CHU, QHU, and total hyperuniformity. — Phase diagrams for the Aubry-André model at system size $N=17711$ and time $t=1$ reveal distinct hyperuniformity classes for CHU, QHU, and total hyperuniformity.

Decoding Criticality: The Language of Scaling

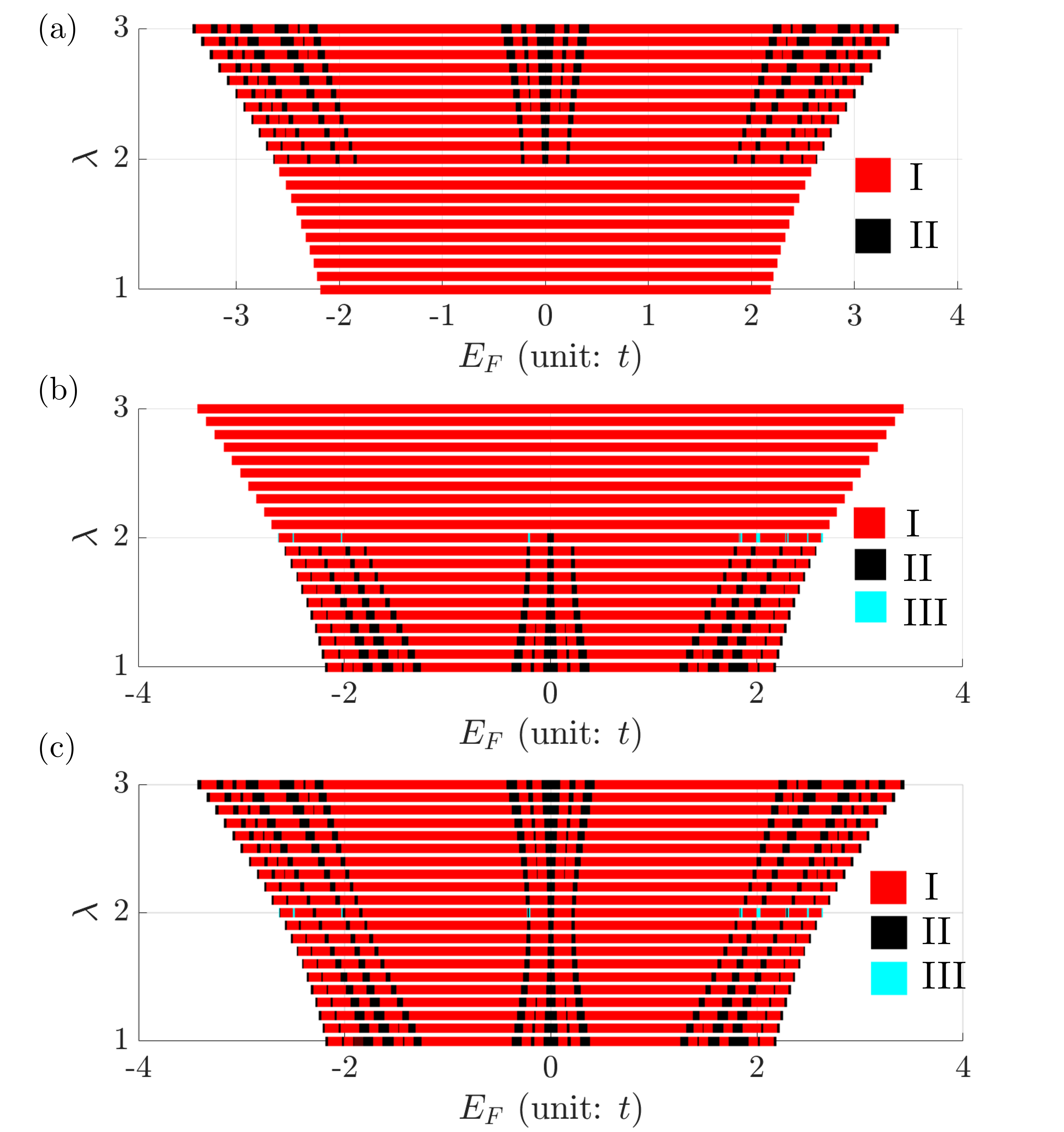
The scaling exponent ν, a defining characteristic of critical phases in condensed matter physics, exhibits a direct correlation with the behavior of the Charge Density Structure Factor (CDSF) in Quasi-Harmonic Universality (QHU) systems. Unlike conventional critical phenomena where ν is typically greater than 1, QHU systems demonstrate a broader range, with observed values of ν falling both below and above 1. Specifically, analysis of the CDSF reveals that ν can equal 2 in certain phases, indicating a unique critical behavior distinct from traditional models. This variability in ν provides a diagnostic tool for identifying and characterizing the critical phase transitions within these systems, as the value of ν is directly determined from the power-law decay of the CDSF in momentum space.

Quasi-harmonic analysis (QHU) extends beyond simply identifying the localization transition; it offers a methodology for characterizing the critical phase itself through scaling analysis. Specifically, the behavior of the Charge Density Structure Factor, as determined by QHU, reveals information about the system’s scaling exponent ν. This exponent, which deviates from the mean-field value, can range from less than 1 to greater than 1, and assumes a value of 2 in specific critical phases. By analyzing how various properties scale with system size – a process facilitated by QHU – researchers can precisely define the universality class of the critical phase and gain insight into its underlying physics, effectively moving beyond mere detection to detailed characterization.

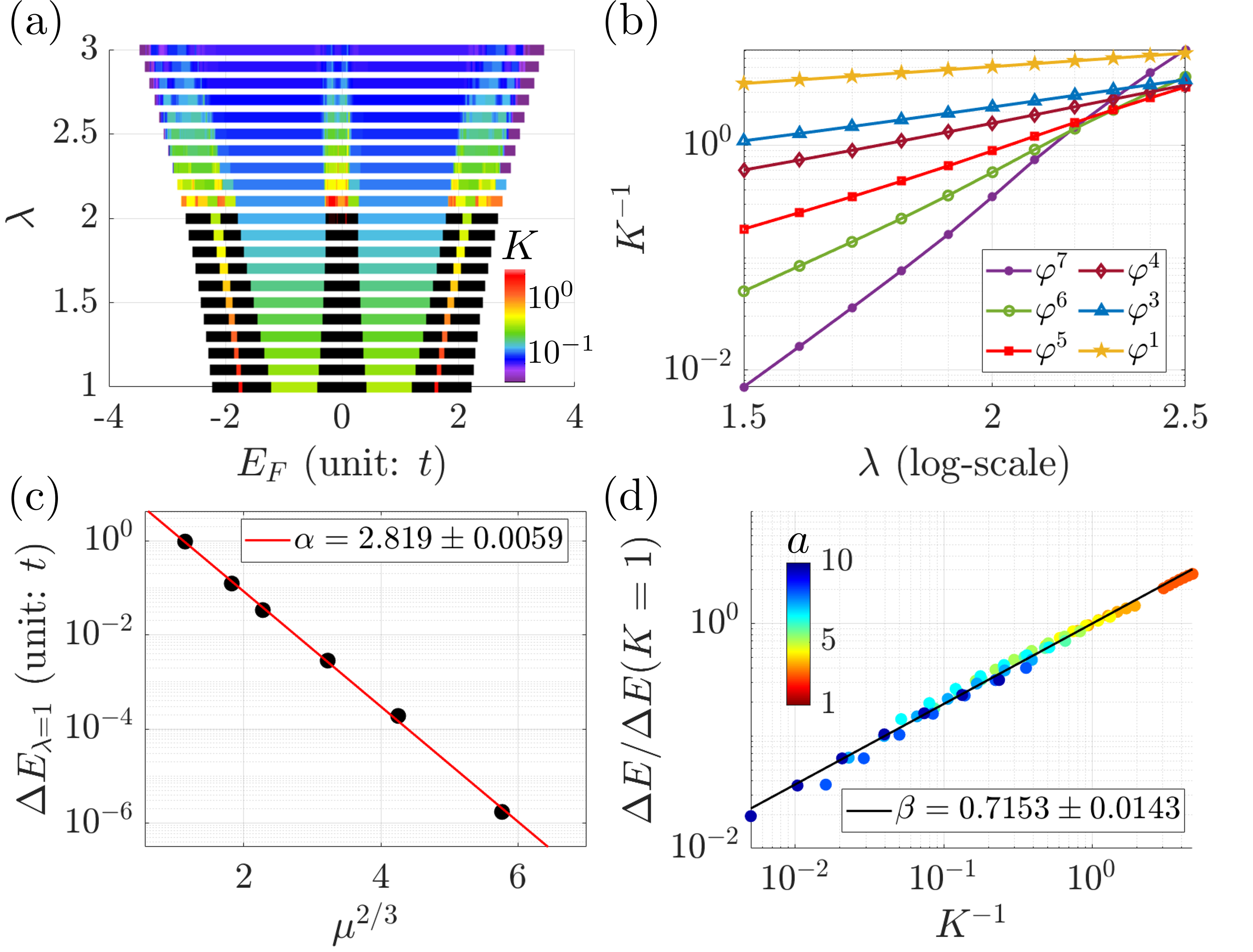
Combining Quasicrystalline Hyperuniformity (QHU) analysis with the Inverse Participation Ratio (IPR) provides a refined characterization of wavefunction localization. The IPR quantifies the degree to which a wavefunction is spatially confined; lower values indicate greater delocalization. Critically, the relationship between the energy gap size and the quantum weight $K$ – a measure of the wavefunction’s intensity at the localization center – can be established through the power law relation: Gap Size ∝ $K^{-β}$ , where β is a universal constant approximately equal to 0.7153. This allows for quantitative assessment of localization strength and provides a link between spectral properties (gap size) and spatial characteristics (quantum weight) of the localized states.

Analysis of the Aubry-André model reveals that quantum weights <span class="katex-eq" data-katex-display="false">K</span> scale as <span class="katex-eq" data-katex-display="false">K \\propto |\lambda|^{-\mu}</span>, with gap sizes <span class="katex-eq" data-katex-display="false">\Delta E</span> exhibiting relationships of <span class="katex-eq" data-katex-display="false">\Delta E_{\lambda=1} \\propto e^{-\alpha \mu^{2/3}}</span> and <span class="katex-eq" data-katex-display="false">K^{-\beta}</span> universal scaling across varying filling fractions and system sizes <span class="katex-eq" data-katex-display="false">N=17711</span>. — Analysis of the Aubry-André model reveals that quantum weights $K$ scale as $K \\propto |\lambda|^{-\mu}$ , with gap sizes $\Delta E$ exhibiting relationships of $\Delta E_{\lambda=1} \\propto e^{-\alpha \mu^{2/3}}$ and $K^{-\beta}$ universal scaling across varying filling fractions and system sizes $N=17711$ .

Beyond Disorder: A Universal Framework for Quantum Phases

Quantum Harris droplet universality (QHU) and its associated scaling behaviors, initially demonstrated in disordered quantum systems, extend surprisingly to a broader range of complex quantum phases. Research indicates these principles aren’t limited to randomness, but are also applicable to systems exhibiting intricate, fractal geometries. This suggests a fundamental connection between the emergence of localized states and the underlying dimensionality of the quantum phase itself, irrespective of whether that dimensionality arises from disorder or inherent structural complexity. The implications are significant, hinting at a unifying framework where the same set of scaling laws can describe the behavior of quantum systems across vastly different physical scenarios – from electrons trapped in disordered potentials to exotic states of matter with non-integer dimensions, potentially revolutionizing the understanding and design of novel quantum materials.

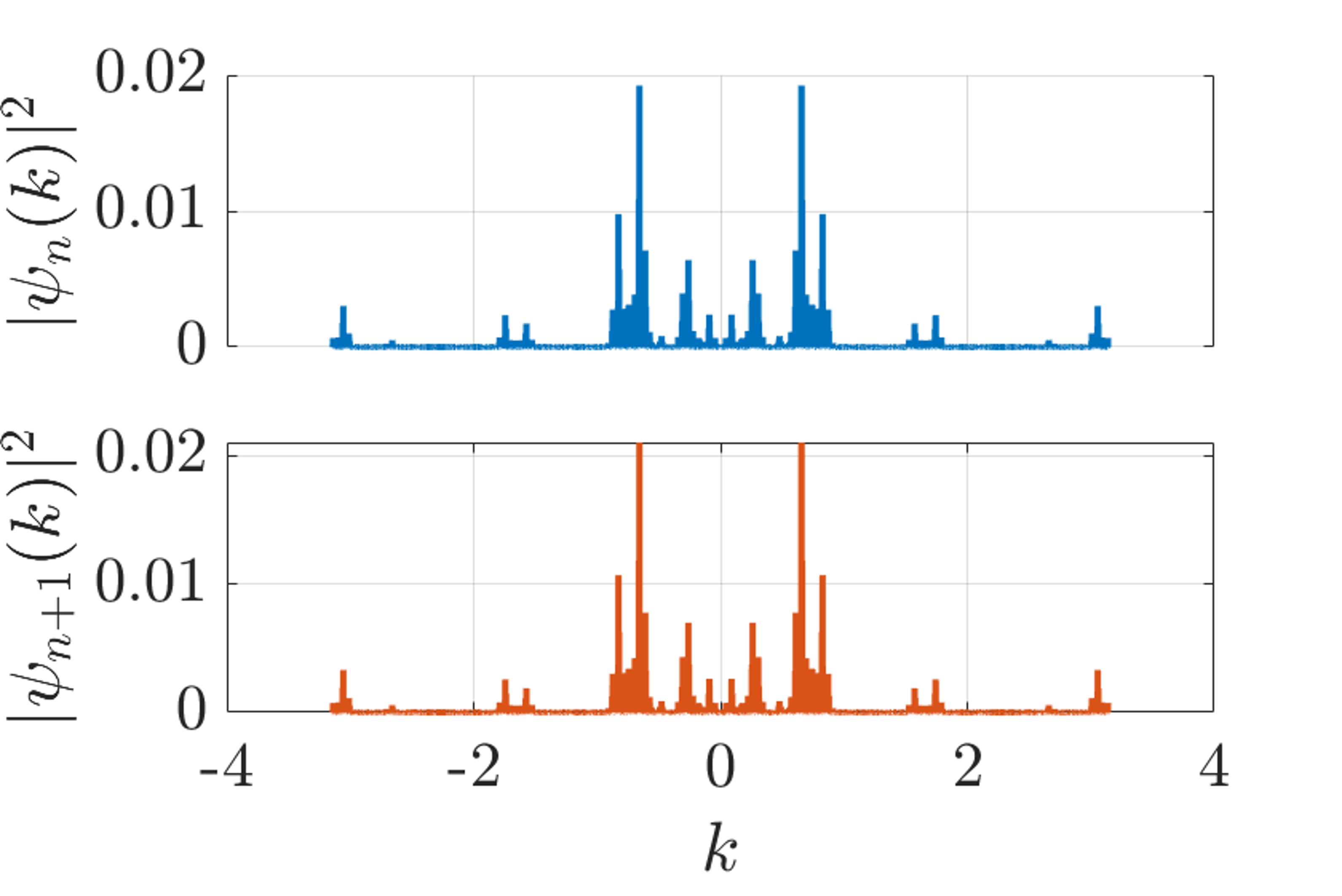
Recent investigations reveal a profound connection between Quantum Hall Universality (QHU), the localization of quantum states, and the intricate structure of wavefunctions in momentum space, offering promising strategies for materials discovery. The spatial extent of a wavefunction directly correlates with its momentum distribution; highly localized states exhibit broad momentum profiles, while extended states possess sharp features. By carefully manipulating these relationships – for instance, through strain engineering or the application of external fields – researchers can tailor the electronic properties of materials. This approach moves beyond simply identifying materials with desirable characteristics; it enables the design of materials with specific, pre-determined quantum behaviors, potentially leading to breakthroughs in areas like superconductivity and topological electronics. Understanding how QHU impacts the momentum space representation of localized states provides a powerful toolkit for predicting and controlling material properties at the quantum level, paving the way for a new era of materials innovation.

A crucial link between a material’s quantum weight, denoted as $K$ , and its energy gap, $\Delta E$ , is emerging as a potent predictive tool in materials science. Recent investigations demonstrate that the energy gap is exponentially related to the quantum weight via the equation $\Delta E \propto e^{- \alpha \mu^2 / 3}$ , where μ represents a system-dependent parameter and α is a constant. This relationship allows researchers to estimate the insulating or conducting behavior of materials-and thus their potential for technological applications-simply by calculating the quantum weight. Unlike complex computational methods, this approach offers a relatively straightforward path to screen candidate materials and guide the design of novel quantum materials with tailored electronic properties, potentially accelerating the discovery of superconductors and advanced semiconductors.

The finite-size fractal dimension of Hamiltonian eigenstates <span class="katex-eq" data-katex-display="false">Eq.(S34)</span> reveals landscape features, while the scaling exponent of <span class="katex-eq" data-katex-display="false">SQ_Q</span> exhibits a dependence on Fermi energy and λ for system size <span class="katex-eq" data-katex-display="false">N=10946</span> with parameters <span class="katex-eq" data-katex-display="false">t_1=1</span> and <span class="katex-eq" data-katex-display="false">t_2=0.3</span>. — The finite-size fractal dimension of Hamiltonian eigenstates $Eq.(S34)$ reveals landscape features, while the scaling exponent of $SQ_Q$ exhibits a dependence on Fermi energy and λ for system size $N=10946$ with parameters $t_1=1$ and $t_2=0.3$ .

The Horizon of Hyperuniformity: Towards a New Quantum Technology

Classical hyperuniformity (CHU) establishes a baseline for understanding spatial order that extends beyond the traditionally crystalline. While often associated with periodic structures, CHU describes systems exhibiting suppressed density fluctuations at all wavelengths, a characteristic also found in certain quantum hyperuniform (QHU) states. This connection isn’t merely coincidental; CHU provides a crucial comparative framework for identifying and characterizing the genuinely quantum mechanical origins of order in QHU systems. By demonstrating that similar suppression of fluctuations can arise from purely classical arrangements, researchers can more rigorously define the uniquely quantum features of these exotic states – distinguishing true quantum order from classical mimicry. This broadened perspective allows for a more nuanced understanding of spatial correlations, ultimately aiding in the design and manipulation of materials with tailored properties, and deepening the exploration of the boundary between order and disorder in both classical and quantum realms.

Quantum hyperuniformity, while already demonstrating surprising connections to seemingly disordered systems, gains further nuance when considered alongside more complex quantum states. Investigations into the relationship between quantum hyperuniformity and phenomena like topological order, many-body localization, and quantum entanglement promise to redefine conventional understandings of order and disorder. It is becoming increasingly clear that hyperuniformity isn’t simply the absence of order, but rather a distinct type of order that can manifest even within highly complex quantum systems. This interplay suggests that spatial correlations, even in the absence of long-range periodicity, can serve as a fundamental organizing principle governing the behavior of matter at the quantum level, potentially revealing hidden symmetries and emergent properties previously obscured by traditional analytical methods. The exploration of these connections may ultimately provide a pathway towards a more complete and unified theory encompassing both order and complexity in the quantum realm.

The deliberate engineering of quantum hyperuniform materials holds immense potential across diverse technological landscapes. By harnessing the principles of quantum hyperuniformity, researchers envision crafting materials with unprecedented control over energy flow and particle interactions. This precision could lead to significant advancements in energy storage, where enhanced efficiency and capacity are paramount; imagine batteries that charge faster and last longer. Furthermore, the unique properties arising from hyperuniformity – such as suppressed density fluctuations and enhanced wave propagation – are ideally suited for building robust and scalable quantum computers. These materials could serve as the foundation for qubits with increased coherence times and reduced error rates, overcoming critical hurdles in the pursuit of practical quantum computation. Beyond these headline applications, the design of hyperuniform structures also promises breakthroughs in areas like advanced sensing, imaging, and metamaterial fabrication, effectively opening new frontiers in materials science and engineering.

The exploration of quantum hyperuniformity, as detailed in this study, reveals a compelling relationship between order and complexity. It echoes a principle of elegant design – that true sophistication arises not from excessive ornamentation, but from the subtle suppression of unnecessary noise. Jürgen Habermas observed, “The medium is not merely a channel for transferring content; it constitutes the very world within which understanding can occur.” Similarly, quantum hyperuniformity doesn’t just indicate a phase transition; it defines the conditions under which coherent quantum behavior-understanding, if you will-can emerge, revealing distinct classes based on the delicate balance of quantum fluctuations. This work demonstrates how identifying and characterizing these fluctuations is paramount to understanding the underlying structure of matter.

Beyond the Horizon

The introduction of quantum hyperuniformity as a diagnostic for quantum phases feels less like a culmination and more like a carefully tuned instrument pointed towards a previously blurred landscape. The immediate success with models like the Aubry-André suggests a sensitivity to subtle order – or, perhaps more interestingly, to the precise absence of conventional order. The true test, however, will lie in its application to systems where the underlying physics is less elegantly constrained, where disorder isn’t a parameter to be dialed, but an inherent property. Consistency is empathy; a metric that fails to illuminate the messy reality of many-body systems is, ultimately, a beautiful distraction.

A persistent question arises: is quantum hyperuniformity merely detecting a localization transition, or is it revealing something deeper about the nature of gapless phases themselves? The connection to suppressed long-wavelength fluctuations hints at a fundamental interplay between order and criticality. Further exploration should focus on extending this framework to higher dimensions and interacting systems, where the signatures of hyperuniformity may be far more elusive.

One suspects that the elegance of the structure factor, so readily interpreted in these initial studies, will give way to complexity as the systems under investigation become less idealized. But it is in that complexity – in the struggle to discern signal from noise – that true understanding resides. Beauty does not distract, it guides attention; and this new tool, while promising, demands rigorous scrutiny and a healthy dose of skepticism.

Original article: https://arxiv.org/pdf/2601.18331.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/