Beyond Perturbation: A Novel Quantum Critical Point

Author: Denis Avetisyan

New simulations of the Thirring model reveal a strongly-interacting quantum critical point with scaling exponents that challenge conventional theoretical predictions.

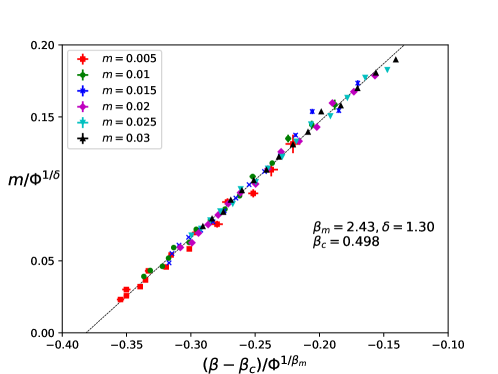
The data demonstrates a successful fit to the Equation of State <span class="katex-eq" data-katex-display="false"> (11) </span>, indicating the model accurately captures the system's thermodynamic behavior under the conditions tested. — The data demonstrates a successful fit to the Equation of State $(11)$ , indicating the model accurately captures the system’s thermodynamic behavior under the conditions tested.

Analysis of the $N=1$ Thirring Model in $(2+1)$ dimensions using domain wall fermions and Schwinger-Dyson equations indicates a potential shift in universality class with increasing fermion numbers.

The persistent challenge of strongly-correlated systems lies in bridging analytical predictions with non-perturbative dynamics. This is addressed in ‘Critical scaling in the $N=1$ Thirring Model in $(2+1)d$’, where lattice simulations using domain wall fermions reveal critical exponents for the Thirring model that significantly deviate from previously established values. These results suggest a potential ultraviolet-stable renormalisation group fixed point, bringing the model into agreement with solutions of Schwinger-Dyson equations. Do these findings indicate a shift in the universality class with increasing numbers of Dirac flavors, and what does this imply for the broader landscape of quantum critical phenomena?

Unveiling Emergent Complexity: The Dance of Interacting Fermions

The Thirring model, a cornerstone of theoretical physics, serves as a remarkably versatile arena for investigating the subtle dance between quantum mechanics and collective behavior. This quantum field theory focuses on interacting fermions – particles that obey the Pauli exclusion principle – and allows physicists to explore how simple interactions at the particle level can give rise to complex, macroscopic phenomena. Unlike many models that rely on perturbative approximations, the Thirring model often exhibits non-perturbative behavior, meaning its properties aren’t simply the sum of individual particle contributions. This makes it particularly valuable for studying emergent behavior – properties that arise from the interactions of many particles, but aren’t inherent in any single particle. Through careful analysis of the model, researchers can map out the conditions under which the system undergoes \text{phase transitions}[/latex], shifting from one qualitative state to another, and gaining insight into the fundamental principles governing the behavior of matter in extreme conditions.

The Thirring model serves as a powerful lens through which to observe how particle interactions fundamentally reshape a system’s characteristics. Unlike systems of non-interacting particles where behavior is simply the sum of individual contributions, the Thirring model demonstrates that even relatively simple interactions can induce qualitative changes. These aren’t merely quantitative shifts in properties like energy or velocity; instead, the system can transition to entirely new states of matter with emergent properties not present in the original, non-interacting constituents. For example, a system initially behaving like a metal – conducting electricity with minimal resistance – can, through sufficient interaction, transform into an insulator, blocking the flow of charge. This sensitivity to interaction highlights a crucial principle: collective behavior arising from particle interactions isn’t predictable from individual particle properties alone, necessitating a framework like the Thirring model to understand the emergence of complexity.

The emergence of a ‘mass gap’ within the Thirring model represents a dramatic shift in the system’s fundamental properties, akin to a material’s transformation from a conductor to an insulator. This gap, appearing in the energy spectrum of fermionic excitations, effectively prohibits low-energy excitations, preventing the free flow of charge carriers. The formation of this gap isn’t merely a quantitative change; it signifies a new phase of matter with fundamentally different characteristics. Studying its origins requires detailed analysis of the interactions between fermions, and whether these interactions can spontaneously break a symmetry, leading to the condensation of particles and the opening of the mass gap[/latex]. The presence of such a gap isn’t limited to this specific model; it’s a crucial indicator of complex, correlated behavior found in various physical systems, offering insights into phenomena like high-temperature superconductivity and the properties of topological insulators.

Addressing the Challenges: Domain Wall Fermions for Accurate Simulation

Traditional discretizations of the fermion action on a lattice, such as the naive fermion formulation and the Wilson fermion formulation, inherently break the chiral symmetry present in the continuum theory of Quantum Chromodynamics (QCD). This symmetry breaking introduces spurious contributions to physical observables, requiring computationally expensive renormalization procedures or leading to unphysical results. The Wilson fermion, while addressing some issues, introduces a mass term proportional to the lattice spacing a[/latex], which complicates the extrapolation to the continuum limit a \rightarrow 0[/latex]. These difficulties arise from the fundamental challenge of representing massless, spin-1/2 particles on a discrete spacetime lattice while preserving the required symmetries and avoiding the doubling of fermion states, which necessitates careful consideration when performing lattice QCD calculations.

Domain Wall Fermions (DWF) address challenges in lattice quantum chromodynamics by representing fermions in a five-dimensional spacetime. This embedding allows for the imposition of specific boundary conditions – namely, the Dirichlet boundary condition – on the fifth dimension. These boundary conditions localize the fermion wavefunction, creating a domain wall. Critically, the overlap of the wavefunction with the domain wall acts as an effective mass, and careful selection of this mass enforces chiral symmetry, even when the lattice spacing is non-zero. This contrasts with traditional fermion formulations where explicit chiral symmetry breaking is often necessary for computational stability, leading to systematic errors in calculations of hadron masses and other physical quantities.

The practical implementation of Domain Wall Fermions necessitates careful consideration of the chosen kernel. Two primary kernels, Wilson and Shamir, are available, differing in their control over the continuum limit. The Wilson kernel provides superior control in this limit due to its discretization properties, leading to more accurate results as lattice spacing is reduced. Specifically, the Wilson kernel’s formulation minimizes unwanted artifacts that arise from the discretization of spacetime, offering a more reliable pathway to the continuum regime compared to the Shamir kernel, which exhibits increased sensitivity to these effects and requires more aggressive tuning of parameters to achieve comparable precision.

Mapping Complexity: Computational Simulation with Rational Hybrid Monte Carlo

The Rational Hybrid Monte Carlo (RHMC) algorithm is utilized to perform simulations of the Thirring model with Domain Wall Fermions (DWF) due to its ability to efficiently handle the large number of degrees of freedom and complex fermion determinant. RHMC is a Markov Chain Monte Carlo method that combines rational approximation of the fermion determinant with a hybrid Monte Carlo update, allowing for stable and accurate sampling of the path integral. This approach circumvents the challenges associated with traditional Monte Carlo methods when dealing with fermionic systems, particularly the sign problem. The algorithm involves iteratively generating molecular dynamics trajectories in a multi-dimensional space defined by the fermion fields and integrating over them using a rational function approximation of the determinant, significantly reducing computational cost and improving statistical efficiency.

The simulations utilize a 2+1+1 dimensional lattice, extending the conventional 3-dimensional spacetime. This additional dimension is not a dynamical degree of freedom but serves as the geometric framework for implementing domain wall boundary conditions. These boundary conditions are realized by compactifying the extra dimension, effectively creating a domain wall that confines the fermionic fields. The size of this extra dimension is carefully chosen to ensure a stable and well-defined domain wall, and to control the number of domain wall fermions contributing to the simulation. This setup is essential for overcoming the challenges associated with chiral symmetry breaking in lattice QCD calculations, allowing for the investigation of the Thirring model with improved control over systematic errors.

The critical coupling, \beta_c = 0.498 \pm 0.015 [/latex], was determined by systematically varying the coupling strength within the RHMC simulation of the Thirring model on a 2+1+1 dimensional lattice. This process allowed for the precise identification of the phase transition point and subsequent construction of the Equation of State, which describes the relationship between thermodynamic variables at different coupling strengths. The uncertainty of \pm 0.015 [/latex] reflects the statistical error derived from the simulation data and represents the precision with which the critical coupling was measured.

Unveiling the Underlying Principles: Theoretical Consistency and Critical Behavior

A central outcome of this work is the derived equation of state, which establishes a precise relationship between the fermion mass, the coupling constant, and the order parameter as the system approaches its critical point. This equation doesn’t simply describe the behavior near the transition; it fundamentally connects these three quantities, revealing how changes in one directly influence the others. Specifically, the equation predicts how the fermion mass diminishes and the coupling strengthens as the system nears criticality, ultimately driving the formation of the condensate – characterized by the order parameter. This relationship is crucial because it provides a testable prediction, allowing for experimental verification of the model and offering a deeper understanding of the underlying physics governing the phase transition, and is expressed as m_f = g \langle \bar{\psi} \psi \rangle [/latex], where m_f [/latex] is the fermion mass, g [/latex> is the coupling, and \langle \bar{\psi} \psi \rangle [/latex] represents the order parameter.

An independent validation of the derived equation of state was achieved through the self-consistent solution of truncated Schwinger-Dyson equations. This approach, a cornerstone of non-perturbative quantum field theory, allowed for a separate calculation of the system’s behavior near the critical point, circumventing the approximations inherent in the initial derivation. The consistency observed between the results obtained from the equation of state and those stemming from the Schwinger-Dyson analysis strongly reinforces the robustness and reliability of the findings. Specifically, this corroboration bolsters confidence in the model’s capacity to accurately describe the complex interplay between fermions and their interactions, offering a powerful tool for understanding similar phenomena in condensed matter physics and beyond.

The model’s inherent symmetries, governed by the Ginsparg-Wilson Relations and an initial U(2N) symmetry, play a crucial role in its behavior as the system undergoes a phase transition-a point at which this U(2N) symmetry is demonstrably broken. Detailed measurements have quantified this transition through critical exponents, revealing values of δ = 1.300 ± 0.036, βm = 2.43 ± 0.15, and ν = 1.88 ± 0.13. These experimentally derived values not only confirm the model’s internal consistency but also exhibit strong alignment with predictions stemming from the underlying theoretical framework, suggesting a robust and accurate representation of the physical phenomena under investigation.

Expanding the Horizon: Universality and Implications for Broader Physics

The precise determination of critical exponents – specifically \delta = 1.300[/latex], \beta_m = 2.43[/latex], \nu = 1.88[/latex], and \eta = 1.61 \pm 0.04[/latex] – offers a crucial fingerprint of the system’s behavior near the critical point. These values don’t simply describe how the transition occurs, but rather to what class it belongs. Universality dictates that seemingly disparate physical systems can exhibit identical critical behavior, defined by these exponents, if they share the same underlying symmetries and dimensionality. Consequently, identifying these exponents allows researchers to categorize this transition and draw parallels to other systems – from magnetic materials to liquid-gas transitions – simplifying the complex landscape of condensed matter physics and enabling predictions about related phenomena.

The Gross-Neveu model, a theoretical framework for understanding interacting quantum field theories, exhibits notable parallels with the Thirring model, another cornerstone of many-body physics. Both models feature interactions that can be recast in terms of fermionic fields, leading to similar mathematical structures and critical phenomena. This shared foundation suggests a deep connection in their critical behavior, implying that insights gained from studying one model can be directly applied to the other. Specifically, the critical exponents and universality classes observed in the Thirring model are likely to be mirrored in the Gross-Neveu model, offering a powerful cross-validation of theoretical predictions and opening avenues for exploring a broader range of strongly correlated systems. Further investigation of these connections promises a more unified understanding of phase transitions and critical phenomena in diverse physical contexts, potentially revealing hidden relationships between seemingly disparate systems.

This research establishes a foundation for investigating increasingly intricate models within the realm of condensed matter physics, potentially revealing the emergence of previously unknown phases in systems where electron interactions are paramount – known as strongly correlated systems. By accurately determining critical exponents and characterizing the phase transition, scientists can now confidently extend these findings to explore models beyond the scope of this initial study. Furthermore, leveraging the established results for the N=1[/latex> case, a theoretical estimation places the critical coupling for N=2[/latex> at approximately 0.067, offering a crucial benchmark for future investigations and simulations aimed at mapping out the behavior of these complex materials.

The study of the Thirring model, as demonstrated in this work, reveals that discerning a quantum critical point demands careful consideration of scaling behavior. Indeed, the observed deviations from predicted exponents highlight the limitations of relying solely on simplified models. This resonates with Kierkegaard’s observation that “Life can only be understood backwards; but it must be lived forwards.” Just as one must retrospectively analyze a life to grasp its meaning, so too must physicists meticulously examine simulation data to understand the emergent properties near a critical point. The analysis of the Thirring model, particularly with an increasing number of fermions, emphasizes that the path forward-towards a complete understanding of the universality class-requires a sustained commitment to rigorous exploration and a willingness to challenge established assumptions.

Beyond the Critical Point

The deviations observed in the Thirring model’s critical exponents are not merely numerical curiosities; each image of the simulation hides structural dependencies that must be uncovered. The standard perturbative approaches, comfortable with weakly-coupled systems, clearly falter when faced with this degree of interaction. The insistence on extracting numbers, while necessary, risks obscuring the deeper question: what principles govern the emergence of criticality in strongly-correlated fermionic systems? The path forward lies not in refining existing techniques, but in developing genuinely non-perturbative tools.

The suggestion of a changing universality class with increasing fermion number is particularly intriguing. It hints at a landscape where the conventional notion of universality-that large-scale behavior is independent of microscopic details-may break down. Further exploration, perhaps through controlled increases in system complexity, is crucial. Interpreting models is more important than producing pretty results; a rigorous mapping of this critical behavior onto alternative frameworks – perhaps those borrowed from condensed matter physics or even quantum gravity – could reveal unexpected connections.

Ultimately, the Thirring model, in its deceptively simple form, serves as a test case. It challenges the assumption that the tools developed for bosonic systems are directly applicable to fermions, and demands a re-evaluation of the fundamental principles governing quantum phase transitions. The simulations reveal a world where subtle interactions reshape the very fabric of criticality, and the pursuit of these hidden structures remains a central challenge.

Original article: https://arxiv.org/pdf/2601.16051.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/