Beyond Perturbation: Unveiling Hidden Structures in Superconformal Field Theories

Author: Denis Avetisyan

New research connects the seemingly complex world of four-dimensional superconformal Yang-Mills theory to a surprisingly simple two-dimensional picture, revealing a deep link between instantons and unstable configurations.

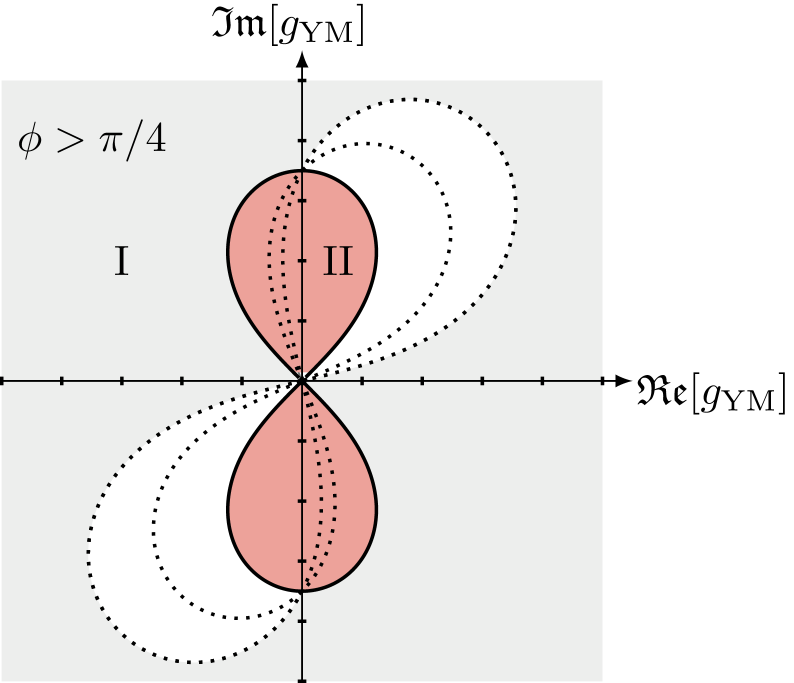
The convergence of <span class="katex-eq" data-katex-display="false">\mathcal{Z}(g\_{\text{YM}},\phi)</span> and <span class="katex-eq" data-katex-display="false">\mathcal{Z}\_{\text{ScYM}}(g\_{\text{YM}},\phi)</span> is dictated by rotational symmetry-a φ rotation of the integration contour induces a corresponding rotation of the divergent region, expanding until, at <span class="katex-eq" data-katex-display="false">\phi=\pi/4</span>, divergence dominates the second and fourth quadrants, after which convergence is localized within figure-eight domains through continued rotation beyond <span class="katex-eq" data-katex-display="false">\arg(a)>\pi/4</span>, with the formal sum of residues converging within the shaded regions and mirrored across the yy-axis for the negative contour. — The convergence of $\mathcal{Z}(g\_{\text{YM}},\phi)$ and $\mathcal{Z}\_{\text{ScYM}}(g\_{\text{YM}},\phi)$ is dictated by rotational symmetry-a φ rotation of the integration contour induces a corresponding rotation of the divergent region, expanding until, at $\phi=\pi/4$ , divergence dominates the second and fourth quadrants, after which convergence is localized within figure-eight domains through continued rotation beyond $\arg(a)>\pi/4$ , with the formal sum of residues converging within the shaded regions and mirrored across the yy-axis for the negative contour.

This work demonstrates that poles in the localized path integral of $\mathcal{N} = 2$ superconformal Yang-Mills correspond to unstable instantons in an embedded 2D gauge theory, providing two complementary interpretations of the same underlying physics.

Despite established techniques for calculating observables in four-dimensional gauge theories, ambiguities arise when analytically continuing localization results beyond their original domain of convergence. This work, ‘The resurgence of errors in the localization of $\mathcal{N} = 2$ superconformal Yang-Mills’, resolves these issues by establishing a surprising connection between the poles of the localized path integral and the spectrum of unstable instantons in a related two-dimensional gauge theory. Specifically, the authors demonstrate that these poles can be interpreted as arising from 2D instanton configurations within a chiral algebra subsector, offering a complementary perspective to traditional Higgs branch localization. Could this duality unlock new methods for non-perturbative calculations in superconformal field theories and provide insights into the broader landscape of resurgence phenomena?

Unlocking the Quantum Vault: The Four-Sphere Partition Function

The partition function in four-dimensional N=2 supersymmetric gauge theory holds a pivotal, yet frustrating, position in theoretical physics. This mathematical object, fundamentally encoding the probabilities of different quantum states, is crucial for understanding a wide range of phenomena, from black hole entropy to the dynamics of strongly coupled systems. However, a direct calculation of this partition function proves remarkably intractable. The integrand involved – a complex, high-dimensional integral over field configurations – is notoriously difficult to handle with conventional path integral techniques. This isn’t simply a matter of computational power; the integrand’s inherent complexity stems from the intricate interplay of supersymmetry and gauge symmetry, necessitating the development of entirely novel mathematical tools and approximation schemes to glean even partial insights from this cornerstone of theoretical investigation. The quest to understand this function drives much of the research in areas like string theory and quantum field theory.

The conventional techniques employed to solve quantum field theories, specifically path integrals, encounter insurmountable obstacles when applied to the four-dimensional N=2 supersymmetric gauge theory. These methods rely on evaluating a highly complex integral – the partition function – which is expressed as a sum over all possible field configurations. The integrand, representing the contribution of each configuration, quickly becomes prohibitively intricate due to the non-perturbative nature of the theory and the presence of instantons-tunneling effects crucial for a complete description. Consequently, direct numerical evaluation or standard analytical approximations prove inadequate, necessitating the development of novel mathematical tools and conceptual frameworks to extract meaningful physical predictions from this otherwise intractable system. The pursuit of these innovative approaches has driven significant advances in areas like localization techniques and topological string theory, offering glimpses into the underlying mathematical structure governing the partition function $Z$ .

For contours within the shaded region where <span class="katex-eq" data-katex-display="false">\pi/4 < \text{arg}(a) < 3\pi/4</span>, the Yang-Mills functional <span class="katex-eq" data-katex-display="false">g_{YM}</span> can be selected to equate the contour integral to the sum of residues, as demonstrated by the highlighted blue path. — For contours within the shaded region where $\pi/4 < \text{arg}(a) < 3\pi/4$ , the Yang-Mills functional $g_{YM}$ can be selected to equate the contour integral to the sum of residues, as demonstrated by the highlighted blue path.

Breaking the Integral: Localization as a Path to Finiteness

Localization techniques in gauge theory provide a method for transforming a typically infinite-dimensional path integral into a finite-dimensional integral defined over the moduli space of the gauge theory. The moduli space parameterizes the different solutions to the classical equations of motion, subject to certain boundary conditions or constraints. By exploiting topological symmetries and focusing on the contributions from these stationary points – solutions to the classical equations – the integral effectively reduces to a sum over these finite number of solutions. This simplification is achieved because the integrand, while complex in the original path integral formulation, becomes concentrated around these stationary points, allowing for a significant reduction in the dimensionality of the integration space and, consequently, computational complexity.

Localization techniques significantly reduce the computational complexity of path integrals by identifying and evaluating integrals at stationary points of the action functional. This process leverages topological symmetries within the gauge theory to restrict integration to a finite-dimensional moduli space, effectively transforming an infinite-dimensional integral into a manageable, finite-dimensional one. The identification of these stationary points, often related to classical solutions like instantons or monopoles, allows for a saddle-point approximation where the integral is dominated by contributions near these points. This drastically lowers the computational cost compared to attempting a full integration over all field configurations, as only the fluctuations around these stationary points need to be considered.

The localized path integral, reduced to an integral over the moduli space, relies heavily on the calculation of one-loop determinants. These determinants arise from fluctuations around the stationary points of the action and are not generally tractable without specific techniques. Monopole Spherical Harmonics provide a basis for representing these fluctuations in gauge theories, particularly those with $N=2$ supersymmetry. Utilizing these harmonics allows for the decomposition of the one-loop determinant into a sum of eigenvalues corresponding to the monopole harmonics’ angular momentum, simplifying the calculation and yielding a finite, computable contribution to the integral. The precise form of these determinants is crucial for determining the physical quantities derived from the path integral, such as partition functions and correlation functions.

Shadows of Non-Perturbation: Poles as Revelations

The localization technique, when applied to calculations of path integrals in supersymmetric gauge theories, frequently results in an integral containing poles in the complex plane. These poles are not artifacts of the calculation but rather signal the presence of non-perturbative effects that are otherwise obscured by the limitations of perturbative expansions. Specifically, the locations of these poles directly correspond to solutions with finite action that are not visible at weak coupling, such as Seiberg-Witten monopoles in $\mathcal{N} = 2$ supersymmetric Yang-Mills theory. The residue at each pole provides information about the contribution of the corresponding non-perturbative object to the overall path integral, effectively allowing for a calculation of effects that would be exponentially suppressed in a perturbative approach.

Resurgent analysis offers a mathematical toolkit for examining the analytic properties of the partition function, particularly its behavior beyond the radius of convergence of the perturbative series. This technique exploits the fact that the partition function, formally represented as a divergent series, possesses a hidden analytic continuation defined through a complex plane. The analytic continuation is not merely a formal extension; it reveals exponentially small, non-perturbative contributions that become significant when approaching singularities – specifically, poles – in the complex plane. By analyzing the residues of these poles, resurgent analysis establishes a precise connection between the perturbative expansion, valid for weak coupling, and the non-perturbative regime, allowing for the calculation of corrections that are otherwise inaccessible through traditional methods. The process relies on identifying a basis of transseries solutions, combining perturbative power series with exponentially suppressed terms $e^{-S/\hbar}$ , where $S$ is a specific action.

The identification of poles within the localized integral is not merely a mathematical curiosity; residue calculations performed at these poles yield direct correspondence to specific physical solutions. Specifically, these poles map onto Seiberg-Witten monopoles, which are non-perturbative solutions to supersymmetric Yang-Mills theory, and unstable instantons. The residue at each pole provides information about the contribution of the corresponding monopole or instanton to the partition function. The magnitude of the residue is directly related to the action of the non-perturbative object, while the location of the pole in the complex plane determines its contribution to the overall quantum effects. This allows for a quantitative link between the analytic structure of the partition function and the spectrum of non-perturbative configurations.

Mirroring Reality: A Two-Dimensional Echo of Four-Dimensional Physics

A remarkable equivalence exists between the complexities of four-dimensional Yang-Mills theory and a significantly simpler two-dimensional counterpart, rooted in their shared partition functions. This isn’t merely an analogy; the mathematical object-the partition function-that encapsulates all possible states of the system is identical in both descriptions. Consequently, calculations that are intractable in the full four-dimensional theory become manageable within the two-dimensional framework, offering a powerful tool for probing the fundamental properties of Yang-Mills interactions. This dimensional reduction doesn’t sacrifice physical insight; rather, it provides an alternative, streamlined approach to understanding a notoriously difficult theory, revealing hidden connections and enabling precise calculations of quantities like $S$ -matrix elements and correlation functions.

A remarkable duality emerges when considering Yang-Mills theories in different dimensions: instantons in the two-dimensional (2d) formulation aren’t merely analogous to features of the four-dimensional (4d) theory, but directly map onto its poles. These instantons, representing tunneling effects in the 2d theory, manifest as singularities in the 4d description, establishing a potent correspondence between the two. This connection isn’t simply a mathematical curiosity; it allows physicists to leverage the relative simplicity of the 2d theory – where calculations are often more tractable – to gain insights into the far more complex 4d Yang-Mills theory, a cornerstone of the Standard Model of particle physics. Effectively, studying instantons in the 2d world provides a unique window into understanding the behavior of the 4d theory at strong coupling, a regime notoriously difficult to explore directly.

A remarkable correspondence arises when considering a specific configuration of the gauge theory: with precisely two flavors of fermions ( $N_f = 2$ ) and a gauge group with four colors ( $N_c = 4$ ), the strength of the interaction in the two-dimensional theory-quantified by the two-dimensional gauge coupling $g_{2d}$ -becomes directly linked to the interaction strength in the original four-dimensional Yang-Mills theory, denoted by $g_{YM}$ . This relationship isn’t merely analogous; the coupling constants are mathematically connected by the equation $g_{2d}^2 = -g_{YM}^2 / (4\pi)$ . The negative sign, while initially surprising, hints at a subtle difference in the mathematical treatment of the theories, and this precise connection allows for calculations performed in the simplified two-dimensional framework to directly inform understanding of the more complex four-dimensional physics, offering a powerful tool for theoretical investigation.

Beyond the Horizon: A Broader Mathematical Landscape

The partition function, a central object in statistical mechanics and quantum field theory, often conceals surprising mathematical connections. Recent investigations reveal the emergence of the Barnes G function within its structure, a special function possessing deep roots in complex analysis and number theory. This isn’t merely a mathematical curiosity; the Barnes G function encodes information about multiple zeta values and polylogarithms, hinting at a profound relationship between seemingly disparate areas of mathematics. Its appearance suggests that the seemingly simple task of counting states in a physical system is intimately linked to sophisticated mathematical machinery, potentially unlocking new avenues for both theoretical physics and pure mathematics. Specifically, the function’s properties, including its analytic continuation and functional equations, provide crucial insights into the behavior of the partition function and the underlying physical system it describes, offering a more complete understanding of its quantum properties and statistical behavior – expressed formally as $G(z+1) = \Gamma(z)G(z)$ .

Investigations into gauge theories reveal that the effective spin of fundamental fields isn’t a fixed property, but rather a dynamic quantity intricately linked to the background geometry and the presence of exotic objects like magnetic monopoles. This means that a field’s intrinsic angular momentum – typically considered a constant – is demonstrably altered by the surrounding spacetime curvature and the topological defects within it. Specifically, the introduction of gauge charges and monopole backgrounds effectively ‘twists’ the field, modifying its spin value and influencing its interactions. This interplay isn’t merely a perturbative effect; it suggests a deeper connection between the field’s quantum mechanical properties and the geometric structure of spacetime, hinting at a framework where geometry and quantum mechanics are fundamentally intertwined and $\hbar$ itself might be emergent from the underlying structure.

A comprehensive grasp of the superconformal theory at the heart of this duality is paramount to broadening the applicability of these techniques. This theoretical framework, extending conventional symmetry concepts, provides a robust set of tools for analyzing strongly coupled systems where traditional perturbative methods fail. By meticulously dissecting the theory’s intricate structure – including its representations, correlation functions, and operator product expansions – researchers can unlock insights into phenomena beyond the reach of simpler approximations. Consequently, a deeper understanding of superconformal principles not only refines existing calculations but also paves the way for tackling more complex physical systems, potentially unveiling novel connections between seemingly disparate areas of theoretical physics – from string theory and quantum field theory to condensed matter physics and even cosmology. The ability to leverage this symmetry to constrain calculations and identify universal behaviors represents a significant step towards a more complete and unified understanding of the physical world.

The study dissects established frameworks, revealing how seemingly divergent physical systems – 4D superconformal gauge theories and 2D gauge theories – are intrinsically linked through unstable instantons. It’s a deliberate probing of the boundaries of localization, questioning whether the poles encountered aren’t signals of a deeper, underlying structure. One finds resonance with the ancient wisdom of Epicurus: “It is not possible to live pleasantly without living prudently and honorably and justly.” The ‘pleasant life’ here isn’t hedonistic, but a harmonious understanding – a ‘just’ mapping – between theoretical constructs, demanding a rigorous, ‘prudent’ examination of the assumptions underpinning the localized path integral and its connection to Seiberg-Witten monopoles.

Beyond the Horizon

The correspondence established here – mapping the poles of a localized path integral to the instability of 2D instantons – feels less like a resolution and more like a carefully constructed invitation. It suggests the current techniques for extracting non-perturbative information from gauge theories are, at best, incomplete glimpses into a more fundamental structure. The real challenge isn’t refining the mapping itself, but dismantling the assumptions that necessitated it. Why rely on a dual description when the original, albeit obscured, theory should, in principle, yield the same answers?

The focus now inevitably shifts to understanding the precise mechanisms driving these instanton instabilities. Are they merely mathematical artifacts of the localization procedure, or do they represent genuine degrees of freedom – perhaps hinting at a deeper connection to Seiberg-Witten monopoles and the chiral algebra? The persistent appearance of 2D physics within this 4D context begs the question: is the true theory inherently two-dimensional, with the higher-dimensional manifestation an emergent property?

One anticipates that extending this analysis to more complex gauge groups and matter content will reveal not just more poles, but more inconsistencies. It is in those very failures – those moments where the mapping breaks down – that the most profound insights are likely to emerge. The game, after all, isn’t about finding the pieces that fit, but about discovering why some refuse to.

Original article: https://arxiv.org/pdf/2602.05733.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/