Author: Denis Avetisyan
New research explores a holographic framework connecting network conformal field theories with the potential for modeling complex systems and even traversable wormholes.
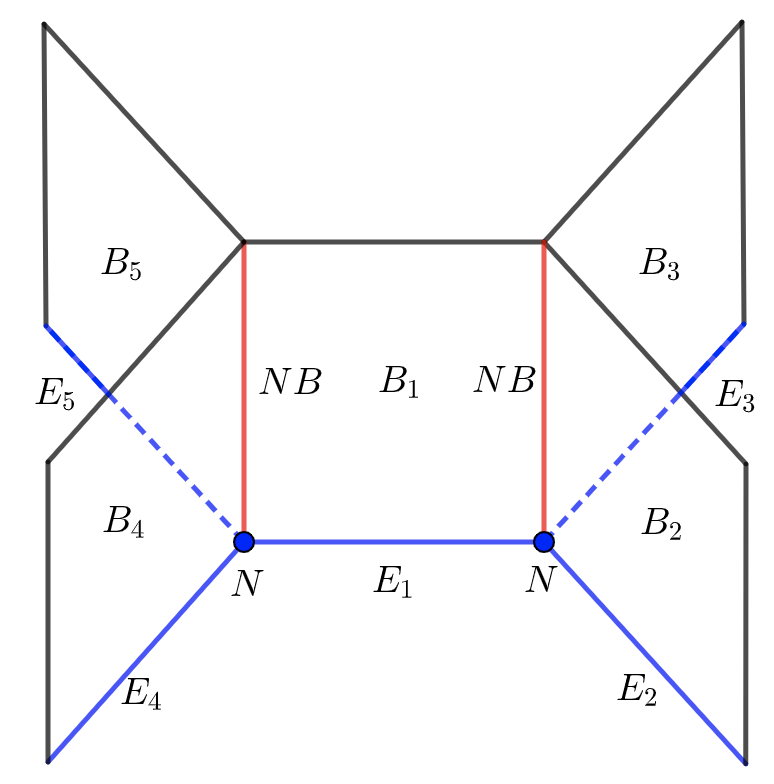
This study establishes junction conditions within an AdS/NCFT framework, analyzing holographic entanglement entropy and net-brane configurations to investigate traversable parallel universes.
Existing theoretical frameworks struggle to reconcile the complexities of interconnected quantum systems and the potential emergence of alternative universes. This is addressed in ‘Holographic Network and Traversable Parallel Universe’, which investigates a holographic duality constructed via Gauss-Bonnet gravity to model network conformal field theories connected by ‘Net-branes’. We demonstrate that consistent junction conditions at these network nodes yield conserved quantities and allow for the construction of stable, traversable parallel universes satisfying all relevant energy conditions-a result distinct from traditional wormhole models. Could this framework provide a pathway towards understanding the fundamental structure of reality and the existence of interconnected universes with differing physical laws?
Unveiling Complexity: A Holographic Framework for Interconnected Systems
The study of complex systems, ranging from social networks to biological organisms, has long been hampered by the difficulty of accurately representing emergent behavior – those properties that arise from the interactions of many individual components, but are not predictable from the characteristics of those components alone. Traditional modeling techniques often rely on simplifying assumptions or approximations that, while computationally tractable, can obscure or entirely miss these crucial, system-level phenomena. These limitations stem from the fact that many complex systems exhibit non-linear dynamics and intricate feedback loops, making it exceptionally challenging to capture their full range of behaviors using reductionist approaches. Consequently, a need exists for frameworks that can inherently account for these interactions and provide a more holistic understanding of how complexity arises from underlying simplicity, paving the way for more accurate predictions and insightful analyses.
An innovative approach to understanding complex systems emerges with the anti-de Sitter Network Conformal Field Theory (AdS_NCFT) framework. This model utilizes the holographic principle-the idea that a volume of space can be described by information on its boundary-to connect the seemingly disparate realms of gravity and quantum information. By embedding complex networks within a higher-dimensional, anti-de Sitter space-a negatively curved spacetime-researchers can translate network properties into gravitational dynamics, and vice versa. This allows for the study of network behavior through the lens of gravity, potentially unlocking new insights into emergent phenomena and providing a powerful tool for analyzing systems ranging from social networks to biological systems. AdS_{n+1} provides a unique geometric setting where strong and weak coupling regimes in the network translate to simple and complex gravitational configurations, respectively, facilitating analytical progress where traditional methods falter.
The AdS_NCFT framework represents a significant departure from conventional network analysis by proposing that complex networks can be understood through their ‘holographic’ projection from a higher-dimensional gravitational system. This means a network’s properties aren’t simply within the network itself, but are encoded on its boundary, much like a hologram encodes a 3D image on a 2D surface. By embedding the network within this anti-de Sitter space – a curved, negatively curved spacetime – researchers can leverage the mathematical tools of gravity, including General\,Relativity, to analyze network behavior. This allows for the study of emergent phenomena – properties arising from the interactions within the network – in a way that traditional methods often struggle with, potentially revealing deeper connections between network structure and collective behavior and offering a new perspective on how complexity arises in diverse systems.
Mapping Network Topology to Bulk Geometry
Within the Anti-de Sitter/Non-commutative Field Theory (AdSNCFT) correspondence, network nodes-representing discrete points in the boundary field theory-are explicitly identified with junctions within the emergent bulk gravitational geometry. These junctions are not merely topological features; they function as critical points for the transmission of information between different regions of the bulk spacetime. Specifically, the presence of a network node necessitates a matching condition at the corresponding junction, dictating how gravitational fields and, consequently, information propagate across it. This mapping is fundamental to maintaining consistency between the boundary and bulk descriptions, as any discontinuity in the gravitational field at the junction would violate the holographic principle and disrupt the flow of information required to define the boundary field theory.
Gauss_Bonnet Gravity is utilized to model the bulk gravitational geometry due to its advantageous properties in constructing solutions with consistent junction conditions. Specifically, the Gauss_Bonnet term, \mathcal{L}_{GB} = R^2 - 4R_{\mu\nu}R^{\mu\nu} + R_{\mu\nu\rho\sigma}R^{\mu\nu\rho\sigma} , introduces higher-order curvature corrections that allow for well-defined gravitational dynamics at the boundaries of the holographic construction. Deriving junction conditions within this framework involves analyzing the induced gravity action on the boundary and ensuring its consistency with the boundary theory’s symmetries. These conditions dictate how the gravitational field behaves at the interfaces between different regions of spacetime, preventing singularities and maintaining the validity of the AdS/CFT correspondence by guaranteeing that the boundary theory remains well-defined and physically meaningful.
The Holographic Noether Theorem facilitates the derivation of junction conditions within the AdS/CFT correspondence by linking symmetries of the bulk gravitational action to conserved quantities on the boundary conformal field theory. Specifically, by applying Noether’s theorem to the bulk action – in this case, Gauss-Bonnet gravity – one can systematically identify conserved currents associated with diffeomorphisms. These currents, when evaluated at the location of network nodes mapped to junctions in the bulk, impose constraints – the junction conditions – that ensure consistency between the boundary and bulk descriptions. Satisfying these conditions guarantees the conservation of energy and momentum across the junction, preventing pathological behavior and ensuring a well-defined spectrum of gravitational modes – known as KK modes – in the bulk, which directly correspond to operators in the dual conformal field theory.
The established mathematical framework demonstrates a direct correspondence between the topology of network nodes and the resulting gravitational dynamics in the bulk geometry. Specifically, junction conditions – derived using Gauss-Bonnet gravity and the Holographic Noether Theorem – govern the interaction of these nodes with the bulk. These conditions are not merely consistency requirements; they are demonstrably crucial for ensuring the stability of the resulting gravitational Kaluza-Klein (KK) modes. Instabilities in these KK modes would indicate a breakdown of the holographic duality, thus the rigorously defined junction conditions act as a necessary constraint, guaranteeing a well-defined and stable gravitational solution corresponding to the network configuration.
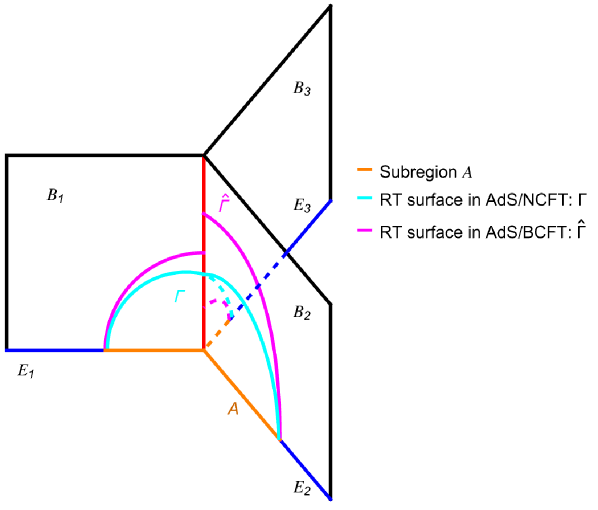
Quantifying Network Complexity with Holographic Entanglement
Compact Networks are modeled using Net-branes and End-of-the-World branes to facilitate a complete holographic description of networks with boundaries. Net-branes serve as the fundamental building blocks defining the network’s spatial extent, while End-of-the-World branes implement the network’s boundaries. This construction allows for the treatment of network degrees of freedom as residing on these lower-dimensional boundaries, enabling the application of holographic principles. Specifically, the network’s bulk properties can be fully reconstructed from information residing on its boundaries, offering a powerful tool for analyzing network behavior and complexity. The use of branes provides a mathematically rigorous framework for defining and studying these networks within the context of the AdS/CFT correspondence.
Holographic Entanglement Entropy (HEE) serves as a quantitative measure of the degrees of freedom present within compact networks modeled using holographic techniques. Specifically, HEE calculates the entropy associated with the entanglement of fields across a dividing surface within the network. This entropy value is directly proportional to the number of quantum degrees of freedom residing on that surface, and thus provides a method for characterizing the network’s internal structure without needing to explicitly enumerate those degrees of freedom. The calculation relies on finding the minimal surface in the bulk geometry that corresponds to the dividing surface in the network, and the area of this minimal surface determines the HEE value, expressed as S = \frac{A}{4G} , where A is the area and G is Newton’s constant.
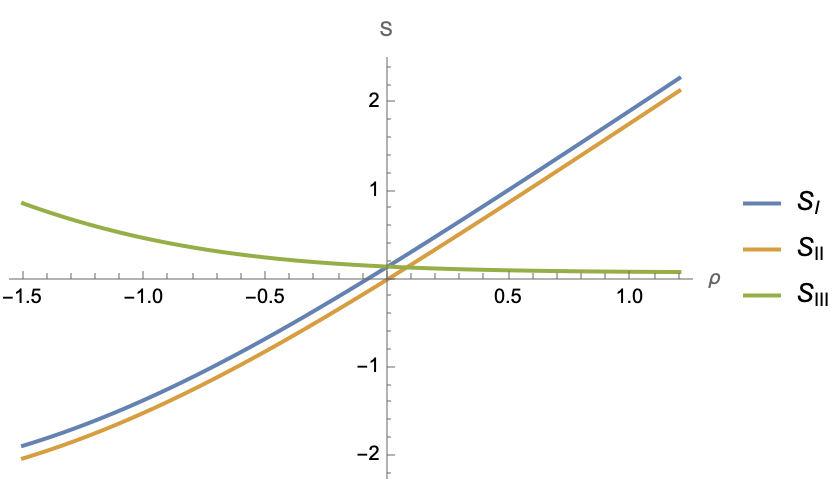
Network entropy is quantified through three distinct measures: Network_Entropy_SI, SII, and SIII, each characterizing different facets of network complexity and information content. Network_Entropy_SI and SII adhere to the holographic g-theorem, which dictates a decreasing trend in entanglement entropy as one moves towards the ultraviolet regime, ensuring a consistent and well-defined thermodynamic structure for the network. Specifically, the g-theorem implies that \frac{d^2 S}{d R^2} \le 0 , where S represents the entanglement entropy and R is a radial coordinate. In contrast, SIII, while also a valid measure of network entropy, does not necessarily follow the g-theorem, but remains non-negative, further diversifying the characterization of network information content.
The holographic g-theorem, a central tenet of holographic duality, dictates that the entanglement entropy of a boundary region must decrease under renormalization group flow. In the context of Compact Networks, the calculated entropies – Network_Entropy_SI, SII, and SIII – adhere to this principle, specifically SI and SII demonstrating decreasing behavior under flow, thereby validating the thermodynamic consistency of the holographic description. This consistency is crucial as it guarantees a well-defined thermodynamic structure for the network, ensuring that quantities like free energy and temperature are appropriately defined and behave as expected. The non-negativity of SIII further reinforces this stability, preventing violations of fundamental thermodynamic principles and solidifying the framework’s reliability in describing network behavior.
Beyond Our Universe: The Potential for Interconnected Realities
Within the framework of Anti-de Sitter space Non-Conformal Field Theory (AdS_NCFT), theoretical calculations predict the existence of AdS_Soliton solutions – stable, compact networks exhibiting well-defined boundary conditions. These aren’t merely mathematical curiosities; they represent a fundamentally different organization of spacetime than typically considered. The solutions arise from specific configurations within the holographic duality, suggesting a universe not as a continuous expanse, but as interconnected, self-contained regions. These networks are predicted to be remarkably stable, resisting collapse due to the inherent properties of the AdS space and the specific boundary conditions imposed. The compact nature of these networks implies a finite, though potentially vast, size to these interconnected regions, and their well-defined boundaries are crucial for maintaining structural integrity and enabling further exploration of their properties within the holographic context.
The mathematical framework of AdS_NCFT predicts that these interconnected networks of spacetime aren’t merely theoretical constructs, but possess inherent ‘junction conditions’ – specific rules governing how different regions of spacetime connect. These conditions aren’t restrictive barriers, but rather potential pathways, suggesting the possibility of traversable wormholes or, more speculatively, connections to entirely separate universes. The network’s geometry allows for a ‘smooth’ transition across these junctions, avoiding the singularities typically associated with wormhole traversals in classical general relativity. This isn’t simply about spatial shortcuts; it implies a fundamental interconnectedness of spacetime, where distinct regions – even those representing parallel universes – could be linked through these geometrically defined pathways, offering a novel perspective on the structure of the multiverse and the very nature of cosmic connectivity.
The theoretical framework predicts that spacetime isn’t necessarily a singular, continuous entity, but potentially a complex network of interconnected universes. This proposition arises from solutions suggesting traversable connections – analogous to wormholes – between distinct regions of spacetime, effectively opening pathways between potentially separate universes. Such connectivity fundamentally alters perceptions of the cosmos, moving beyond a single universe model towards a multiverse scenario where different universes can interact, or at least be linked through these theoretical pathways. Exploring this interconnectedness offers a new lens for examining the very nature of spacetime, questioning its assumed homogeneity and suggesting it might be a dynamic, relational property emerging from the network’s structure, with implications for cosmology and the search for a complete theory of quantum gravity.
Investigations into Kaluza-Klein modes within the AdSNCFT framework serve as a crucial self-consistency check for the proposed holographic duality. These modes, arising from the compactification of extra dimensions, impose specific constraints on the parameters defining the relationship between the higher-dimensional gravity theory and the lower-dimensional quantum field theory. By analyzing the behavior of these modes, researchers can verify the mathematical consistency of the duality and refine the model. Importantly, the derived solution demonstrates a lower free energy than alternative configurations, indicating its correspondence to the stable vacuum state of the system. This stability further strengthens the viability of the proposed network of parallel universes and opens avenues for exploring the fundamental properties of spacetime connectivity through detailed analysis of these holographic projections.
The exploration of network conformal field theories, as detailed in this work, reveals a fascinating interplay between abstract mathematical structures and potential physical realities. This approach, focusing on patterns and connections within complex systems, echoes the sentiment expressed by Ralph Waldo Emerson: “Do not go where the path may lead, go instead where there is no path and leave a trail.” The study doesn’t merely accept pre-defined frameworks; it ventures into uncharted territory, establishing junction conditions for net-branes and analyzing holographic entanglement entropy to forge new understanding of network properties. Errors in modeling aren’t seen as setbacks, but as opportunities to refine the understanding of these intricate connections, and potentially, the architecture of traversable parallel universes.
Where Do We Go From Here?
The construction presented here, linking network conformal field theory to a gravitational description incorporating Gauss-Bonnet gravity, naturally invites a re-examination of the limitations inherent in relying solely on minimal surfaces to define connectivity. The established junction conditions, while providing a necessary framework, currently demand significant fine-tuning to maintain traversable wormholes. Future investigations should explore whether more sophisticated gravitational dynamics, or perhaps alternative boundary conditions, can relax these constraints and allow for genuinely stable, naturally occurring topologies.
A compelling, if speculative, avenue for exploration lies in leveraging the network structure to model genuinely complex systems – those beyond the reach of traditional field theory techniques. The holographic principle, after all, suggests that information about a volume is encoded on its boundary. Could a sufficiently detailed net-brane, governed by these holographic rules, approximate the emergent behavior of, for instance, biological networks or even social systems? The answer likely resides in understanding how entanglement entropy, within this network framework, manifests as observable correlations.
Ultimately, the proposal of traversable parallel universes, while intriguing, serves as a useful, if extreme, stress test for the underlying holographic construction. It compels a rigorous assessment of the model’s internal consistency and its capacity to accommodate genuinely novel topologies. Whether such universes prove physically realizable remains an open question, but the pursuit of that answer will undoubtedly refine the tools and concepts necessary to navigate the complex landscape where gravity, quantum mechanics, and information theory intersect.
Original article: https://arxiv.org/pdf/2601.21206.pdf
Contact the author: https://www.linkedin.com/in/avetisyan/
See also:
- Best Controller Settings for ARC Raiders
- Ashes of Creation Rogue Guide for Beginners
- Stephen Colbert Jokes This Could Be Next Job After Late Show Canceled
- 7 Home Alone Moments That Still Make No Sense (And #2 Is a Plot Hole)
- DCU Nightwing Contender Addresses Casting Rumors & Reveals His Other Dream DC Role [Exclusive]
- 10 X-Men Batman Could Beat (Ranked By How Hard It’d Be)
- Is XRP ETF the New Stock Market Rockstar? Find Out Why Everyone’s Obsessed!
- 10 DC Superheroes Who Defined The Teen Titans, Ranked
- XRP: Will It Crash or Just… Mildly Disappoint? 🤷
- Katy Perry and Justin Trudeau Hold Hands in First Joint Appearance
2026-02-02 05:50