Beyond Spin: Geometric Origins of Magnetization

Author: Denis Avetisyan

New research reveals a hidden source of magnetization in quantum materials arising not from electron spin, but from the curvature of momentum space.

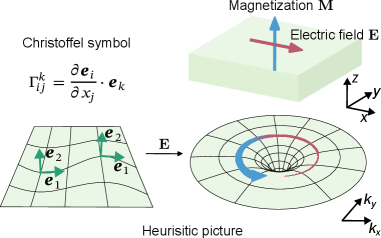
Nonlinear magnetization arises from an induced curvature in quantum space-analogous to the Christoffel symbols describing transformations in curved spacetime-which drives electron orbital motion and results in a magnetization proportional to the square of the applied electric field.

This work introduces the quantum Christoffel symbol to describe a nonlinear orbital magnetization independent of spin-orbit coupling and linked to the Berry curvature in topological materials.

Conventional understanding of magnetization typically relies on spin-orbit coupling and broken inversion symmetry. Here, in ‘Quantum Christoffel Nonlinear Magnetization’, we report the discovery of a distinct nonlinear orbital magnetization in quantum materials, characterized by a geometric quantity – the quantum Christoffel symbol – defined within the Hilbert space of quantum states. This emergent magnetization arises from the curvature of momentum space and is independent of conventional mechanisms, potentially manifesting in materials like BiF$_3$ and Ru$_4$Se$_5$. Could this novel interplay between geometry and magnetism unlock new paradigms for controlling and detecting quantum phenomena via optical and transport measurements?

The Geometry of Spacetime and Quantum States

Einstein’s theory of General Relativity fundamentally reimagines gravity not as a force, but as a manifestation of the curvature of spacetime. This curvature isn’t arbitrary; it’s mathematically described by the $Christoffel\ symbol$ , a set of coefficients that quantify how the coordinate system itself changes from point to point within spacetime. These symbols, derived from the metric tensor which defines distances, allow physicists to calculate the geodesic – the shortest path between two points in curved spacetime – which objects follow under the influence of gravity. Essentially, massive objects warp the geometry of spacetime around them, and other objects move along the curves created by this warping. This geometric interpretation elegantly explains phenomena like the bending of light around massive objects and the subtle precession of planetary orbits, replacing Newtonian gravity with a far more nuanced and accurate model of the universe.

The traditionally geometric description of spacetime, foundational to General Relativity, is finding echoes in the seemingly disparate realm of quantum mechanics through the concept of the Quantum Metric. This mathematical tool defines a distance not within physical space, but between quantum states – the fundamental descriptions of a quantum system. Unlike classical distances, the Quantum Metric isn’t about spatial separation, but rather the dissimilarity between these states, quantifying how much one state must change to become another. Researchers posit that this isn’t merely an analogy; the very structure of quantum information, and potentially the emergence of spacetime itself, may be rooted in these geometric relationships between quantum states. $g_{ij}$ – the components of the Quantum Metric – effectively provides a way to measure the ‘quantum geometry’ of the system, suggesting a deep, and potentially unifying, connection between the fabric of spacetime and the fundamental building blocks of quantum reality.

Emergent Quantum Properties: Orbital Magnetization and Berry Curvature

Orbital magnetization arises from the cumulative effect of electron orbital angular momentum within a material, and is not simply a sum of individual atomic contributions. This macroscopic magnetization is fundamentally connected to the Berry curvature, $\Omega_n(k)$ , a property defined in reciprocal space (k-space) that describes the geometric phase acquired by an electron’s wavefunction as it moves through the Brillouin zone. The Berry curvature effectively acts as a fictitious magnetic field experienced by electrons, influencing their dynamics and contributing to various quantum phenomena. A non-zero Berry curvature, and therefore a non-trivial Berry phase, implies the existence of topological band structures and is directly proportional to the change in the wavefunction phase with respect to changes in the electron’s momentum in k-space. Consequently, the integral of the Berry curvature over a closed loop in k-space is quantized, directly linking it to observable physical quantities like orbital magnetization and anomalous Hall conductivity.

Wave Packet Dynamics and the Boltzmann Equation are complementary computational techniques used to characterize orbital magnetization and Berry curvature in materials. Wave Packet Dynamics directly simulates the time evolution of an electron’s wave function under periodic potential, allowing for the precise calculation of Berry curvature as the integral of the fictitious magnetic field $\mathbf{B} = \nabla \times \mathbf{A}$ , where $\mathbf{A}$ is the vector potential. The Boltzmann Equation, conversely, provides a semi-classical approach, treating electrons as quasi-particles subject to external forces and scattering events; its solution yields the distribution function from which both orbital magnetization and Berry curvature contributions to transport phenomena can be determined. While Wave Packet Dynamics is computationally intensive but highly accurate, the Boltzmann Equation offers a more tractable method for analyzing complex systems and larger length scales, often requiring approximations for scattering rates and band structure details.

The Quantum Anomalous Hall Effect (QAHE) is characterized by the appearance of quantized Hall conductance, specifically $e^2/h$ , in the absence of an external magnetic field. This phenomenon arises from the intrinsic Berry curvature within the material’s band structure, effectively mimicking the role of an external field. The Berry curvature acts as an effective magnetic field in momentum space, leading to the chiral edge states responsible for dissipationless current flow and the observed quantization. Materials exhibiting QAHE typically require specific band structures with non-trivial topology and strong spin-orbit coupling to generate the necessary Berry curvature and support this unique state of matter.

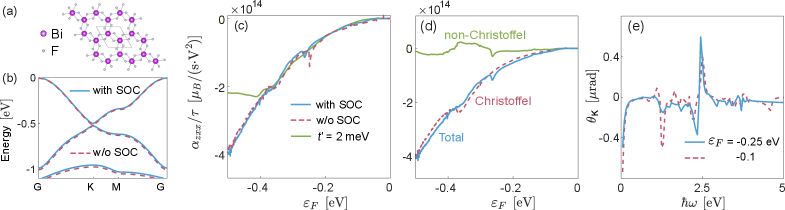
First-principles calculations reveal that the 2D BiF3 lattice structure and band structure, incorporating spin-orbit coupling and a Haldane-like perturbation, exhibit a significant nonlinear magnetization coefficient <span class="katex-eq" data-katex-display="false">\alpha_{zxx}</span> dependent on Fermi energy and a corresponding Kerr rotation angle that directly probes magnetization. — First-principles calculations reveal that the 2D BiF3 lattice structure and band structure, incorporating spin-orbit coupling and a Haldane-like perturbation, exhibit a significant nonlinear magnetization coefficient $\alpha_{zxx}$ dependent on Fermi energy and a corresponding Kerr rotation angle that directly probes magnetization.

The Geometric Origin of Nonlinear Response

Nonlinear Orbital Magnetization (NOM) describes a material response where the induced magnetization is not directly proportional to the applied electric field. In materials exhibiting NOM, the magnetization $M$ responds to an electric field $E$ such that $M \propto E^n$ , where $n > 1$ . This deviates from the linear, or dielectric, response commonly observed, and arises from the complex interplay between electronic band structure and orbital currents. The magnitude of the nonlinear response is dependent on material properties like the density of states and the specific symmetry of the electronic bands, indicating that NOM is not a universal phenomenon but rather a characteristic of specific materials and conditions.

The nonlinear response observed in orbital magnetization to applied electric fields is accurately described by the Quantum Christoffel Symbol, which provides a geometric interpretation of this relationship. This symbol, derived from the system’s band structure, directly connects the electric field-induced changes in orbital magnetization, effectively quantifying the nonlinear susceptibility. Calculations demonstrate that the contribution of the Quantum Christoffel Symbol to the overall nonlinear response significantly outweighs that of any non-Christoffel terms, establishing it as the dominant mechanism governing this behavior. The magnitude of this effect is directly related to the curvature of the band structure in momentum space, specifically $\nabla \times \mathbf{F}$ , where $\mathbf{F}$ is the Berry connection.

The observation of nonlinear orbital magnetization, described by the Quantum Christoffel Symbol, is fundamentally linked to the properties of materials exhibiting Particle-Hole Symmetry and Dirac Fermions. Particle-Hole Symmetry dictates a correspondence between electron and hole excitations, influencing the system’s response to external fields. Dirac Fermions, characterized by their linear energy dispersion, contribute to enhanced sensitivity to these fields. Consequently, manipulation of quantum transport phenomena becomes possible through control of the electric field-induced nonlinear orbital magnetization, offering potential avenues for device applications reliant on precise control of electron flow and spin dynamics within these materials.

The nonlinear magnetization coefficient <span class="katex-eq" data-katex-display="false">\alpha_{zxx}</span>-calculated using an effective model [Eq. (B1)]-exhibits complex dependencies on the Fermi energy, particle-hole symmetry breaking parameter, and tight-binding parameter, demonstrating how symmetry variations impact this material property, as illustrated by comparisons of band structures with and without particle-hole symmetry. — The nonlinear magnetization coefficient $\alpha_{zxx}$ -calculated using an effective model [Eq. (B1)]-exhibits complex dependencies on the Fermi energy, particle-hole symmetry breaking parameter, and tight-binding parameter, demonstrating how symmetry variations impact this material property, as illustrated by comparisons of band structures with and without particle-hole symmetry.

Bismuth Trifluoride: A Promising Material Platform

Bismuth trifluoride (BiF₃) presents a promising material platform for the study of Nonlinear Orbital Magnetization (NOM) due to its specific electronic configuration. The Bi³⁺ ion possesses a lone pair of 6s electrons which, combined with the strong spin-orbit coupling inherent in bismuth, results in a substantial mixing of spin and orbital degrees of freedom. This electronic structure leads to a large orbital magnetic moment and a pronounced response to electric fields, enhancing the material’s susceptibility to NOM effects. Furthermore, BiF₃ crystallizes in a relatively simple structure, facilitating both theoretical modeling using techniques like Density Functional Theory and experimental characterization of its nonlinear optical properties.

Density Functional Theory (DFT) calculations are fundamental to understanding the electronic structure of BiF₃, providing the ground state energy, electron density, and band structure necessary for analyzing its properties. Specifically, the use of Wannier Functions, post-processing DFT results, allows for the construction of tight-binding models and the accurate description of orbital polarization and hybridization. These models are crucial for predicting the material’s response to external stimuli, such as electromagnetic radiation, by enabling the calculation of relevant quantities like the nonlinear optical susceptibility tensor. The combination of DFT and Wannier Functions facilitates the determination of the electronic band structure and the identification of key orbital contributions to the nonlinear optical response, thereby providing a theoretical framework for interpreting experimental observations.

Detection of the Kerr Effect in BiF₃ would serve as direct experimental confirmation of the theoretically predicted nonlinear magnetization response. This magneto-optical effect manifests as a rotation of the polarization plane of light reflected from the material when subjected to a magnetic field. Computational modeling suggests a Kerr rotation angle on the order of a few micro-radians (μrad) for BiF₃, a magnitude considered readily measurable with standard magneto-optical Kerr effect (MOKE) instrumentation and techniques. Successful observation and quantification of this rotation would therefore validate the accuracy of the Density Functional Theory and Wannier function calculations used to predict the material’s nonlinear optical properties.

Toward Quantum Technologies and Beyond

The precise manipulation of quantum states through nonlinear magnetization offers a promising pathway for advancements in both spintronics and quantum information processing. This technique leverages the geometric properties of electron spins, allowing for control beyond traditional electrical or magnetic fields. By carefully tailoring the material’s magnetization-specifically exploiting its nonlinear response-researchers can sculpt and direct quantum information carriers, potentially leading to more robust and efficient quantum bits, or qubits. This approach circumvents some limitations of conventional methods, offering greater stability against decoherence and enabling the creation of complex entangled states crucial for quantum computation. Furthermore, the ability to geometrically control spins opens doors for novel spintronic devices with enhanced functionality, such as ultra-sensitive magnetic sensors and energy-efficient data storage, potentially revolutionizing data handling and processing technologies.

The pursuit of materials displaying Flat-Band Superconductivity and Fractional Chern Insulator properties promises a substantial leap forward in the geometric control of quantum states. These exotic materials, characterized by their unique electronic band structures, offer enhanced nonlinear magnetization responses due to the increased density of states near the Fermi level. Specifically, Flat-Band Superconductivity provides a robust platform for maintaining coherence, while Fractional Chern Insulators introduce topologically protected edge states that can be harnessed for manipulating quantum information. Combining these features with existing techniques could lead to the creation of more efficient and stable quantum devices, potentially unlocking advanced functionalities in spintronics and quantum computation. The inherent robustness of these states against disorder and external perturbations offers a pathway toward scalable and fault-tolerant quantum technologies, exceeding the limitations of current material systems.

The ability to control quantum states through nonlinear magnetization signifies a fundamental departure from conventional methods of quantum manipulation, potentially revolutionizing fields reliant on precise quantum control. This approach doesn’t simply refine existing techniques; it introduces a novel mechanism where the material’s internal magnetic properties directly dictate quantum behavior, bypassing the need for external fields in certain applications. Crucially, estimations place the magnitude of this nonlinear magnetization at 10^-4 μ_B, a value considered substantial enough to induce measurable and controllable effects on quantum systems. This relatively strong nonlinearity suggests the possibility of creating robust and efficient quantum devices, and paves the way for innovations in spintronics, quantum computing, and beyond, by offering a new degree of freedom for tailoring quantum interactions.

The pursuit of fundamental properties within quantum materials demands a stripping away of unnecessary complexity, a focus on the underlying geometric essence. This research, detailing a nonlinear orbital magnetization governed by a quantum Christoffel symbol, exemplifies this principle. It reveals a phenomenon independent of spin-orbit coupling, isolating a core geometric effect within momentum space. As Stephen Hawking once stated, “Intelligence is the ability to adapt to any environment.” This adaptation, in the context of condensed matter physics, manifests as the ability to discern fundamental mechanisms-like this magnetization-from the noise of extraneous interactions, achieving clarity through focused investigation of quantum geometry.

Where to Now?

The identification of a magnetization effect stemming from momentum-space geometry, divorced from the usual suspect of spin-orbit coupling, necessitates a reassessment of established frameworks. The quantum Christoffel symbol, as presented, is not merely a mathematical curiosity; it suggests a previously unacknowledged channel for manipulating magnetic properties through band structure engineering. The immediate challenge lies in experimental verification, a pursuit complicated by the predicted subtlety of the effect. Existing techniques may prove inadequate, demanding novel probes sensitive to these geometric contributions.

The current work offers a compelling argument for a more holistic understanding of magnetization. It invites consideration of whether similar geometric mechanisms underpin other, seemingly unrelated, phenomena in topological materials. A crucial direction will involve exploring the interplay between this nonlinear magnetization and established concepts like the anomalous Hall effect. Disentangling these contributions-determining where geometry ends and conventional physics begins-will be no small task.

Ultimately, the elegance of this discovery resides in its reductionism. A complex phenomenon, magnetization, is traced back to a fundamental property of momentum space. Further research should embrace this principle, striving not for increasingly intricate models, but for ever-simpler explanations. The goal is not to add layers of complexity, but to reveal the underlying unity of physical laws.

Original article: https://arxiv.org/pdf/2602.03597.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/