Beyond Steady State: How Quantum Systems Retain Memory of Their Past

Author: Denis Avetisyan

New research reveals that open quantum systems don’t simply settle into a stable state, but continue to be influenced by their initial conditions and transient dynamics.

The study demonstrates how quasiprobability distributions, calculated from trajectory-eigenstate overlaps, reveal the stochastic time evolution of quantum systems-specifically, an XXZ chain defined by equations $11$ and $12$ with parameters $N=4$, $\Delta=0.7$, and $J^{\prime}$ varying between $2.0$ and $0.5$, and a Bose-Hubbard dimer described by equations $24$ and $25$ with $N_c=3$, $F=3$, and $\Delta$ ranging from $2.5$ to $8$-suggesting that even seemingly well-defined quantum models are subject to inherent uncertainties in their probabilistic representation.

The full spectrum of the Liouvillian superoperator governs the late-time behavior of open quantum systems, demonstrating persistent delocalization of quantum trajectories.

Conventional wisdom posits that the late-time dynamics of open quantum systems are dominated solely by the steady state and slowest-decaying modes, yet this work-‘Localization and Delocalization of Quantum Trajectories in the Liouvillian Spectrum’-demonstrates a surprising persistence of influence from the full Liouvillian spectrum. By analyzing individual quantum trajectories, we reveal that these trajectories can remain delocalized across transient eigenstates even after reaching a steady state, challenging the notion of complete decoherence into the stationary subspace. This delocalization correlates strongly with the purity of trajectory-averaged observables, establishing a novel connection between individual quantum trajectories and ensemble descriptions. Could a more complete understanding of this spectral influence unlock new strategies for controlling open quantum systems and harnessing their non-equilibrium dynamics?

The Illusion of Isolation: Quantum Systems and Their Surroundings

The foundations of quantum mechanics are often presented with the assumption of isolated systems, entities perfectly shielded from external influences. However, this is largely a theoretical idealization; in reality, every quantum system inevitably interacts with its surrounding environment. These interactions, however subtle, constitute a continuous exchange of energy and information, blurring the boundaries between the system and its surroundings. Consider a single atom – it isn’t truly alone, but constantly bombarded by electromagnetic radiation, jostled by thermal fluctuations, and influenced by the presence of other particles. These environmental ‘couplings’ are not merely perturbations to be ignored; they fundamentally shape the system’s behavior, preventing it from evolving in the pristine, predictable manner dictated by the Schrödinger equation in isolation. Consequently, understanding and modeling these interactions is crucial for accurately describing the dynamics of any real-world quantum system, from microscopic particles to macroscopic devices.

The relentless interaction between a quantum system and its surroundings introduces dynamics that deviate from the predictable, isolated evolution described by unitary transformations. This interplay isn’t merely a perturbation; it fundamentally reshapes the system’s behavior through a process called decoherence. Decoherence effectively diminishes quantum superposition and entanglement – the very features that distinguish quantum mechanics – as information leaks into the environment. Consequently, a system’s quantum state collapses into a classical-like mixture, exhibiting probabilistic behavior governed by the density matrix $ \rho $. This transition from coherent quantum evolution to decoherent, classical-like behavior is not a failure of quantum mechanics, but rather an inevitable consequence of its application to realistic, open systems constantly exchanging energy and information with their surroundings.

The conventional Schrödinger equation, predicated on the principle of unitary evolution, proves insufficient when modeling realistic quantum systems. These systems invariably interact with their surroundings, leading to the exchange of energy and information-a process fundamentally described by non-unitary dynamics. To accurately represent this interplay, physicists employ techniques like the Lindblad master equation and quantum trajectory methods. These approaches introduce dissipation and decoherence terms, effectively accounting for the system’s entanglement with its environment and the resulting loss of quantum coherence. Consequently, the system’s state is no longer governed by a simple, predictable evolution, but rather by a probabilistic description reflecting the influence of external interactions and the inevitable transition towards classical behavior. This shift in perspective is crucial for understanding phenomena ranging from the operation of quantum technologies to the behavior of molecules in complex chemical environments.

The Language of Open Systems: Density Matrices and the Liouvillian

The density matrix, denoted as $\rho$, offers a complete state description for quantum systems, particularly those interacting with an environment – termed ‘open’ systems. Unlike the wave function, which fully describes a closed quantum system, $\rho$ is a $N \times N$ matrix, where $N$ is the dimension of the Hilbert space. It accounts for both pure states – represented by a single ket $| \psi \rangle$ where $\rho = | \psi \rangle \langle \psi |$ – and mixed states, which are probabilistic ensembles of pure states. A mixed state is represented as a convex combination: $\rho = \sum_{i} p_{i} | \psi_{i} \rangle \langle \psi_{i} |$, where $p_{i}$ are probabilities and $\sum_{i} p_{i} = 1$. Crucially, $\rho$ fully characterizes the system’s quantum state, including effects like decoherence and dissipation arising from environmental interactions, which are not captured by the pure state formalism.

The time evolution of the density matrix, $\rho(t)$, for an open quantum system is determined by the Master Equation: $d\rho(t)/dt = -i\mathcal{L}\rho(t)$, where $\mathcal{L}$ is the Liouvillian operator. This operator encapsulates all system-environment interactions and dissipation processes. The Liouvillian is not necessarily Hermitian; its eigenvalues generally possess negative real parts, corresponding to decay rates of system coherence and population imbalances. Solving the Master Equation allows for the prediction of the system’s state at any given time, accounting for both unitary dynamics and non-unitary effects arising from the environment. The form of the Liouvillian depends on the specific system-environment coupling and the employed approximations, such as the Born-Markov approximation.

The eigenbasis of the Liouvillian operator, often denoted by the set of eigenstates {$L_i$}, provides critical insight into the time evolution of an open quantum system. Each eigenstate $L_i$ is associated with an eigenvalue $\gamma_i$, which represents the rate at which the corresponding state either decays to equilibrium or contributes to persistent oscillations. Analyzing this eigenbasis allows for the decomposition of the system’s initial density matrix into a superposition of these fundamental modes. Consequently, the time evolution of the density matrix can be determined directly from the contribution of each eigenstate, weighted by its corresponding eigenvalue. Steady states of the system correspond to the zero-eigenvalue (or null space) components of the Liouvillian, representing states that do not change with time. Therefore, identifying the Liouvillian’s eigenbasis is essential for predicting system behavior and characterizing its long-term stability.

Analysis of the XXZ spin chain reveals that both the center of mass and inverse participation ratio exhibit time-dependent behavior, demonstrated through averages across multiple trajectories with standard deviation indicated, and further detailed by single-trajectory insets, mirroring parameter sets from prior analysis.

Simulating the Unseen: From Quantum Trajectories to Circuits

Quantum trajectories offer a stochastic approach to solving the Master Equation, which describes the time evolution of an open quantum system’s density matrix, $ \rho $. Instead of directly evolving $ \rho $, the trajectory method represents the system’s state as a collection of individual, pure state wavefunctions, $|\psi_i(t)\rangle$, each associated with a specific realization of the system’s random environment. The evolution of each trajectory is governed by a stochastic Schrödinger equation, and the ensemble average of these trajectories recovers the solution to the original Master Equation. This ‘unraveling’ allows for the simulation of open system dynamics using techniques typically reserved for closed quantum systems, effectively replacing a complex operator equation with an ensemble of simpler, deterministic equations for pure states.

The Monte Carlo Wavefunction (MCWF) method facilitates the simulation of quantum trajectories by stochastically sampling wavefunctions that satisfy the Schrödinger equation coupled to a bath environment. This is achieved through the introduction of random jumps corresponding to the measurement of bath degrees of freedom, allowing for the efficient calculation of expectation values and time evolution without explicitly solving for the entire density matrix. The method scales favorably with system size, making it a practical technique for simulating open quantum systems where traditional approaches become computationally prohibitive. Specifically, the MCWF method generates an ensemble of trajectories, each representing a possible evolution path, and utilizes these trajectories to estimate the system’s properties, effectively replacing the complex integration required in solving the Master Equation with a statistical sampling process.

Non-Hermitian Random Quantum Circuits offer a distinct methodology for simulating open quantum system dynamics by directly implementing the effects of environmental interactions within a quantum computation. These circuits utilize complex-valued circuit elements, specifically allowing for non-Hermitian Hamiltonians, to model dissipation and decoherence without explicitly simulating an environment. The dynamics are governed by a stochastic process derived from random matrix theory, where each circuit application represents a time step in the evolution of the open system. By repeatedly applying these random circuits to an initial quantum state, the system’s density matrix can be efficiently approximated, providing a computationally tractable alternative to solving the Master Equation or employing trajectory-based methods. This approach is particularly suited for near-term quantum devices as it avoids the resource overhead associated with encoding and simulating a large environment.

Analysis of the XXZ chain reveals that steady-state purity, concurrence (CM), and information propagation rate (IPR) exhibit consistent qualitative behavior across varying parameters, with concurrence and IPR decreasing as purity increases, as demonstrated by heatmaps and trajectory-averaged data.

Symmetry, Localization, and Entanglement: Signatures of Open System Behavior

Quantum systems interacting with their environment, known as open quantum systems, can display symmetries distinct from those found in isolated, or ‘closed’, systems; these are termed ‘weak symmetries’. This arises because the environmental interaction effectively alters the system’s Hamiltonian, introducing new constants of motion or modifying existing ones. Consequently, a system that might appear to lack symmetry when considered in isolation can exhibit symmetry when its interaction with the environment is accounted for. This phenomenon is not merely a theoretical curiosity; it fundamentally impacts the system’s dynamics and steady-state properties, influencing everything from energy transport to the stability of quantum phases. Understanding these weak symmetries is crucial for accurately modeling and predicting the behavior of real-world quantum devices, which are invariably coupled to some external reservoir.

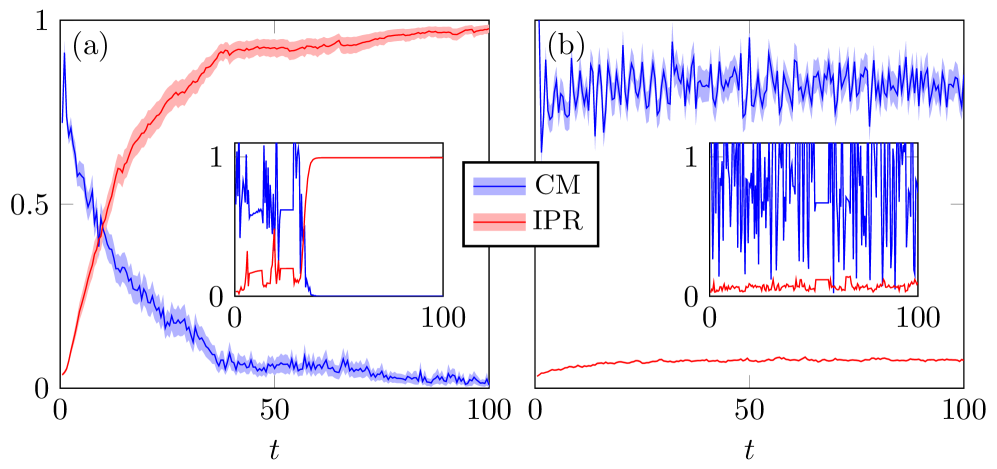
The behavior of open quantum systems can be understood by examining how quantum states localize, a characteristic quantified by the Inverse Participation Ratio (IPR). Calculated from the numerous possible quantum trajectories a system can take, the IPR effectively measures the ‘spread’ of a state – a high IPR indicates a highly localized state, while a low value suggests a more delocalized one. Research demonstrates a strong correlation between this localization, as determined by the IPR, and the purity of the system’s steady state – the state it settles into over time. This purity is further characterized by two related metrics: the Center of Mass, reflecting the average position of the quantum state, and, crucially, another calculation of the Inverse Participation Ratio applied to the steady state itself. A highly pure steady state correlates with both a low Center of Mass and a high steady-state IPR, indicating a concentrated, localized final condition, while mixed states exhibit opposite characteristics, revealing fundamental insights into the system’s dynamics and its response to external influences.

Analysis of the Bose-Hubbard and Heisenberg XXZ chains, employing techniques that quantify localization and symmetry, demonstrates a clear connection between entanglement and symmetry breaking. These models exhibit transitions between distinct phases characterized by varying degrees of entanglement, reflected in the steady state purity – ranging from nearly pure states ($1$) to mixed states with lower purity. This purity is not arbitrary; it correlates directly with the Center of Mass, which indicates the system’s spatial distribution, and the Inverse Participation Ratio, a measure of state localization. A high Inverse Participation Ratio – approaching $1$ – signifies a localized state, while lower values indicate delocalization, and these values shift in tandem with changes in the Center of Mass and the overall system purity as parameters are adjusted, revealing the underlying phase transitions and how symmetry is broken or restored.

The behavior observed in Figure 3 also applies to the Bose-Hubbard chain with parameters J and U.

Beyond Equilibrium: Transient Dynamics and the Path Forward

The evolution of a quantum system immediately following a disturbance isn’t random, but rather dictated by its Liouvillian’s transient eigenstates. These eigenstates aren’t solutions for long-term behavior, but instead detail the precise way a quantum state unravels or decays in the brief moments after being perturbed. Essentially, they provide a ‘snapshot’ of the system’s short-time dynamics, revealing how initial conditions influence its immediate future. Analyzing these transient states allows researchers to understand how a system loses memory of its initial preparation, and how quickly it approaches a steady state. This understanding is crucial because many quantum processes, such as energy transfer or the response to external fields, occur on timescales where these transient dynamics dominate, and classical approximations break down. Furthermore, characterizing these eigenstates provides a foundation for predicting and controlling the system’s behavior, potentially leading to advancements in quantum information processing and spectroscopy.

The abstract mathematical framework of the Liouvillian, while powerful for describing quantum decay, benefits from connection to real-world measurements through the concept of quasi-probabilities. These functions, though not strictly probabilities due to their potentially negative values, offer a bridge between the Liouvillian’s eigenbasis-which details how quantum states evolve-and the probabilities of detecting specific outcomes in quantum experiments. By carefully interpreting these quasi-probabilities, researchers can reconstruct possible quantum trajectories, essentially charting the paths a quantum system could take during its evolution. This connection is crucial because it allows theoretical predictions derived from the Liouvillian to be tested against experimental observations, ultimately validating the model and enabling a deeper understanding of non-equilibrium quantum dynamics. Furthermore, this approach opens avenues for designing and controlling complex quantum systems by manipulating these trajectories and optimizing the likelihood of desired outcomes.

The progression of quantum research is poised to leverage recently developed tools for analyzing transient dynamics to tackle increasingly complex systems. Investigations are shifting towards applying the Liouvillian framework and associated quasi-probability methods to areas like many-body physics, open quantum systems, and non-equilibrium phenomena. This analytical approach promises a deeper understanding of system evolution beyond simple energy considerations, potentially enabling the design of more robust and efficient quantum technologies. Future studies aim to harness these insights for advancements in quantum control, error correction, and the development of novel quantum materials, ultimately bridging the gap between theoretical foundations and practical applications in fields such as quantum computing and sensing.

The study of open quantum systems, as detailed in this paper, reveals a persistent dance between localization and delocalization, even in established steady states. It seems the system resists complete resolution, echoing a fundamental uncertainty. This echoes Erwin Schrödinger’s observation that, “The task is, first, to understand what we mean by ‘reality’.” The paper demonstrates how transient eigenstates continue to exert influence, implying that any description of the system’s final state is necessarily incomplete. Any model constructed to describe these quantum trajectories is merely an echo of the observable, and beyond the reach of full comprehension, everything disappears. The Liouvillian spectrum, it appears, is less a definitive map and more a testament to the limits of knowing.

Where Do the Trajectories Lead?

The persistence of delocalized quantum trajectories, even within the supposed finality of the steady state, suggests a discomforting truth about the Liouvillian spectrum. Each measurement is a compromise between the desire to understand and the reality that refuses to be understood. The full spectrum isn’t merely a mathematical construct; it appears to be an active participant in late-time dynamics, a ghostly echo of transients that refuses to fully dissipate. This work highlights the limitations of focusing solely on the eigenvalues associated with the steady state-a natural inclination, perhaps, but one that risks overlooking a richer, more unsettling reality.

Future investigation must confront the question of how these delocalized trajectories-influenced by the entire Liouvillian spectrum-manifest in observable phenomena. Quasiprobabilistic approaches, while useful, may only offer a partial glimpse; a deeper theoretical framework is needed to reconcile the persistence of transient effects with the apparent irreversibility of open quantum systems. It is possible that the very notion of a definitive ‘steady state’ is an illusion, a convenient fiction constructed to avoid acknowledging the universe’s fundamental impermanence.

The exploration of entanglement, particularly its role in mediating these long-lived dynamics, seems a promising avenue. One does not uncover the universe-one tries not to get lost in its darkness. Perhaps the most valuable outcome of this line of inquiry will not be a complete description of open quantum systems, but a humbling realization of the limits of description itself.

Original article: https://arxiv.org/pdf/2511.19700.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/