Beyond the Dirac Cone: Unveiling Interactions in Exotic Fermions

Author: Denis Avetisyan

New research explores how long-range interactions reshape the behavior of type-II semi-Dirac fermions, impacting their fundamental properties.

The evolution of power <span class="katex-eq" data-katex-display="false">\eta(E)</span> within the density of states <span class="katex-eq" data-katex-display="false">\rho(E) \sim E^{\eta(E)}</span> demonstrates a transition from linear Dirac behavior at low energies to type-II semi-Dirac characteristics as energy increases, a phenomenon modulated by interaction strengths of <span class="katex-eq" data-katex-display="false">\alpha = 0.05, 0.10, 0.20</span> at the Hartree-Fock level and consistent with the interacting spectrum detailed previously. — The evolution of power $\eta(E)$ within the density of states $\rho(E) \sim E^{\eta(E)}$ demonstrates a transition from linear Dirac behavior at low energies to type-II semi-Dirac characteristics as energy increases, a phenomenon modulated by interaction strengths of $\alpha = 0.05, 0.10, 0.20$ at the Hartree-Fock level and consistent with the interacting spectrum detailed previously.

This review details the renormalization group analysis of interacting type-II semi-Dirac quasiparticles and reveals tunable density of states with consequences for Landau level quantization and thermodynamic observables.

Conventional descriptions of emergent fermions often assume weak interactions, neglecting the profound impact of long-range Coulomb forces. This work, ‘Interacting type-II semi-Dirac quasiparticles’, investigates the consequences of these interactions on type-II semi-Dirac fermions-quasiparticles arising in topologically nontrivial systems-revealing a tunable density of states that evolves from linear to a power-law of $|\varepsilon|^{1/3}$ . We demonstrate that this interaction-driven transformation fundamentally alters key physical characteristics, manifesting in non-universal scaling of observables like Landau levels. How might these modified low-energy excitations influence the design of novel electronic devices and materials with tailored properties?

Beyond Conventional Electronics: Unveiling Semi-Dirac Fermions

The limitations of conventional electronic materials stem from their inherent rigidity in accommodating the demands of increasingly complex device functionalities. Traditional semiconductors, while reliable, often struggle to adapt to the need for greater energy efficiency, faster processing speeds, and novel device architectures. This inflexibility arises from the fixed nature of electron behavior within these materials; electrons are typically treated as either massless or possessing a constant mass, hindering the creation of devices capable of dynamically responding to external stimuli. Consequently, researchers are actively exploring materials that allow for greater control over electron behavior, seeking to overcome these limitations and unlock possibilities beyond the scope of current silicon-based technology. This pursuit necessitates the investigation of novel quasiparticles, such as semi-Dirac fermions, which offer a pathway toward more versatile and adaptable electronic components.

Semi-Dirac fermions represent a fascinating departure from conventional electronic behavior, existing as quasiparticles that blend characteristics of both massless and massive particles. Unlike typical electrons, which possess a defined mass and energy-momentum relation, these fermions exhibit a linear energy dispersion in one direction and a quadratic dispersion in another-a unique anisotropy that dictates their movement and interactions. This peculiar behavior arises from specific material structures and symmetries, enabling the possibility of tailoring electronic properties beyond those achievable with standard semiconductors. The resulting electronic states are highly sensitive to external stimuli, suggesting potential applications in advanced devices such as high-speed transistors, novel sensors, and even topological quantum computing, where the manipulation of these unique fermions could unlock entirely new functionalities and overcome limitations of current electronic technologies.

The realization of next-generation electronic devices hinges on the ability to understand and control semi-Dirac fermions, quasiparticles exhibiting a unique blend of massless and massive behaviors. Unlike conventional electrons confined by established band structures, these fermions respond to external stimuli in novel ways, potentially enabling devices with enhanced flexibility and efficiency. Current research focuses on manipulating material structures – often through complex layering or strain engineering – to precisely tailor the properties of these fermions. This includes controlling their velocity, spin, and interactions, with the ultimate goal of creating transistors and circuits that surpass the limitations of silicon-based technology. Successfully harnessing semi-Dirac fermions promises a paradigm shift in electronics, opening doors to devices with unprecedented functionality and performance characteristics – from flexible displays to ultra-sensitive sensors and beyond.

The static polarization function for type-II semi-Dirac fermions reveals a ravine at <span class="katex-eq" data-katex-display="false">p_y = (c_1/c_2)^{3}p_x^{3/2}</span> that separates regions dominated by <span class="katex-eq" data-katex-display="false">p_x^{1/2}</span> and <span class="katex-eq" data-katex-display="false">p_y^{1/3}</span> dependence, as demonstrated by constant-<span class="katex-eq" data-katex-display="false">p_x</span> and <span class="katex-eq" data-katex-display="false">p_y</span> contours calculated with <span class="katex-eq" data-katex-display="false">c_1 = 0.196\pi</span>, <span class="katex-eq" data-katex-display="false">c_2 = 0.154\pi</span>, and <span class="katex-eq" data-katex-display="false">w = 50</span>. — The static polarization function for type-II semi-Dirac fermions reveals a ravine at $p_y = (c_1/c_2)^{3}p_x^{3/2}$ that separates regions dominated by $p_x^{1/2}$ and $p_y^{1/3}$ dependence, as demonstrated by constant- $p_x$ and $p_y$ contours calculated with $c_1 = 0.196\pi$ , $c_2 = 0.154\pi$ , and $w = 50$ .

Bilayer Graphene: A Fertile Ground for Semi-Dirac Fermions

Bilayer graphene’s band structure differs significantly from that of single-layer graphene, creating conditions conducive to hosting semi-Dirac fermions. While graphene exhibits a linear dispersion relation leading to massless Dirac fermions, the van der Waals interaction between graphene layers in bilayer structures introduces interlayer coupling. This coupling results in a modified dispersion relation with differing group velocities for the conduction and valence bands, but without a complete gap opening. Consequently, the resulting low-energy excitations behave as semi-Dirac fermions, possessing a finite density of states at the Dirac point – a characteristic absent in conventional Dirac fermions and impacting the material’s electronic and transport properties. The band structure can be further described by a $2 \times 2$ Hamiltonian, allowing for detailed analysis of the resulting fermion characteristics.

Interlayer sliding in bilayer graphene refers to the relative displacement of the two graphene layers comprising the structure. This mechanical manipulation directly impacts the electronic band structure, specifically by modifying the overlap between the π orbitals of adjacent layers. Controlled sliding can induce a linear dispersion near the Dirac point, resulting in the formation of semi-Dirac fermions characterized by a vanishing density of states at the Dirac point and a modified Fermi velocity. The degree of interlayer displacement acts as a tuning parameter, allowing for control over the carrier concentration and the resulting electronic transport properties of the bilayer graphene system.

Accurate modeling of bilayer graphene’s electronic behavior under interlayer sliding requires a comprehensive understanding of its Hamiltonian. The Hamiltonian, a mathematical operator describing the total energy of the system, must account for the interactions between the layers and the resulting modifications to the Dirac equation. Specifically, the interlayer coupling strength and the induced potential difference due to sliding significantly alter the energy dispersion relation and, consequently, the fermion characteristics. Variations in these parameters necessitate adjustments to the Hamiltonian to correctly predict the emergence of semi-Dirac cones and the associated changes in carrier mobility and density of states. $H = H_0 + V_{interlayer}$ , where $H_0$ represents the unperturbed Hamiltonian and $V_{interlayer}$ describes the interlayer interaction, is a fundamental representation used in these calculations.

The Hamiltonian <span class="katex-eq" data-katex-display="false">\mathcal{H}=\\left(g\\_{1}k\\_{x}^{2}-vk\\_{y}+\\Delta\\right)\\hat{\\sigma}\\_{x}+g\\_{2}k\\_{x}k\\_{y}\\hat{\\sigma}\\_{y}</span> exhibits a transition from three Dirac cones (<span class="katex-eq" data-katex-display="false">\Delta < 0</span>) to a type-II semi-Dirac point at the origin (<span class="katex-eq" data-katex-display="false">\Delta = 0</span>), and finally to a shifted band crossing and type-II semi-Dirac behavior at higher energies (<span class="katex-eq" data-katex-display="false">\Delta > 0</span>). — The Hamiltonian $\mathcal{H}=\\left(g\\_{1}k\\_{x}^{2}-vk\\_{y}+\\Delta\\right)\\hat{\\sigma}\\_{x}+g\\_{2}k\\_{x}k\\_{y}\\hat{\\sigma}\\_{y}$ exhibits a transition from three Dirac cones ( $\Delta < 0$ ) to a type-II semi-Dirac point at the origin ( $\Delta = 0$ ), and finally to a shifted band crossing and type-II semi-Dirac behavior at higher energies ( $\Delta > 0$ ).

Decoding the Electronic Landscape: Many-Body Effects and Spectrum Renormalization

The electronic properties of bilayer graphene are substantially modified by the Coulomb interaction between electrons, resulting in a renormalization of the energy spectrum. This interaction, arising from the long-range nature of the Coulomb potential, leads to shifts in the energy levels and alters the relationship between energy and momentum. Specifically, the bare energy dispersion $E_0(k)$ is modified to an interacting dispersion $E(k)$ , effectively changing the system’s band structure. This renormalization is not a simple energy shift; it affects the density of states and, consequently, the material’s optical and transport characteristics, necessitating theoretical approaches that account for many-body effects beyond single-particle approximations.

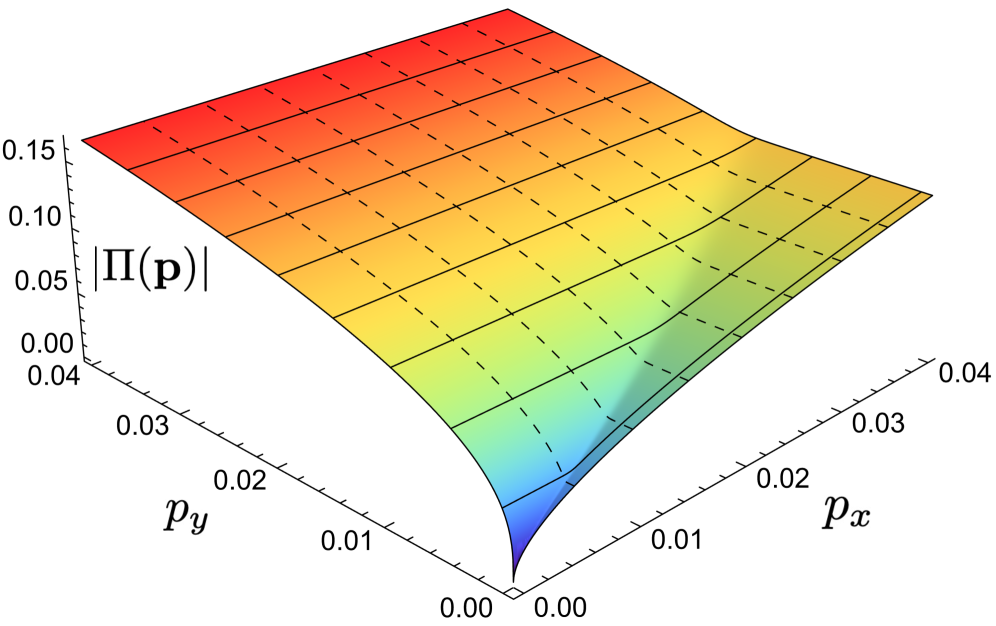
A comprehensive understanding of electron-electron interactions in bilayer graphene necessitates the use of many-body perturbation theory. This approach calculates the effects of interactions beyond the single-particle approximation by iteratively applying a perturbation to the non-interacting Hamiltonian. Crucially, the direct Coulomb interaction is modified by dielectric screening, accurately modeled using the Random Phase Approximation (RPA). The RPA introduces a frequency-dependent dielectric function that accounts for the collective response of the electrons to external perturbations, effectively reducing the strength of the Coulomb interaction. The polarization function, $\Pi(q, \omega)$ , describes the induced electron density in response to a perturbation at wavevector $q$ and frequency ω, and is central to calculating the screened Coulomb interaction within the RPA. This combination of perturbation theory, RPA screening, and the polarization function provides a reliable framework for determining the many-body effects influencing the electronic band structure and overall material properties.

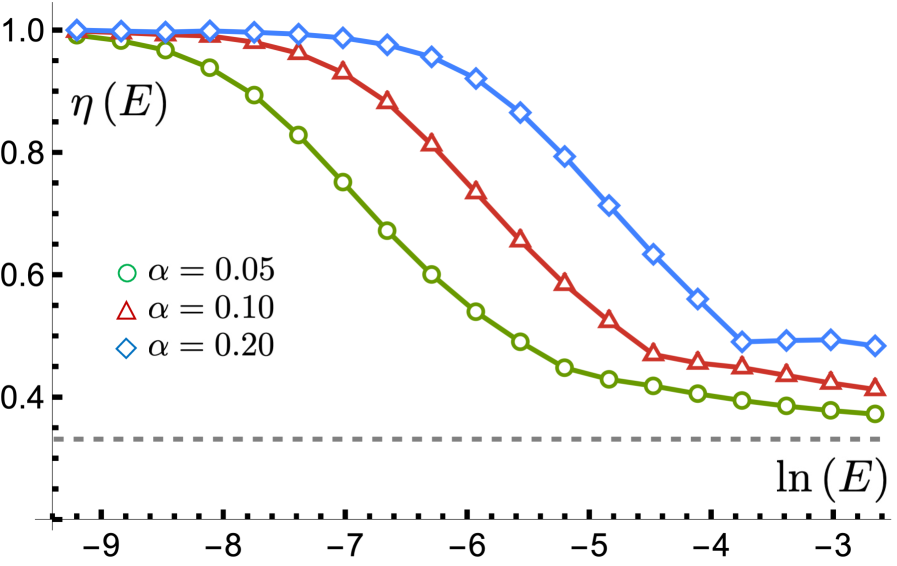
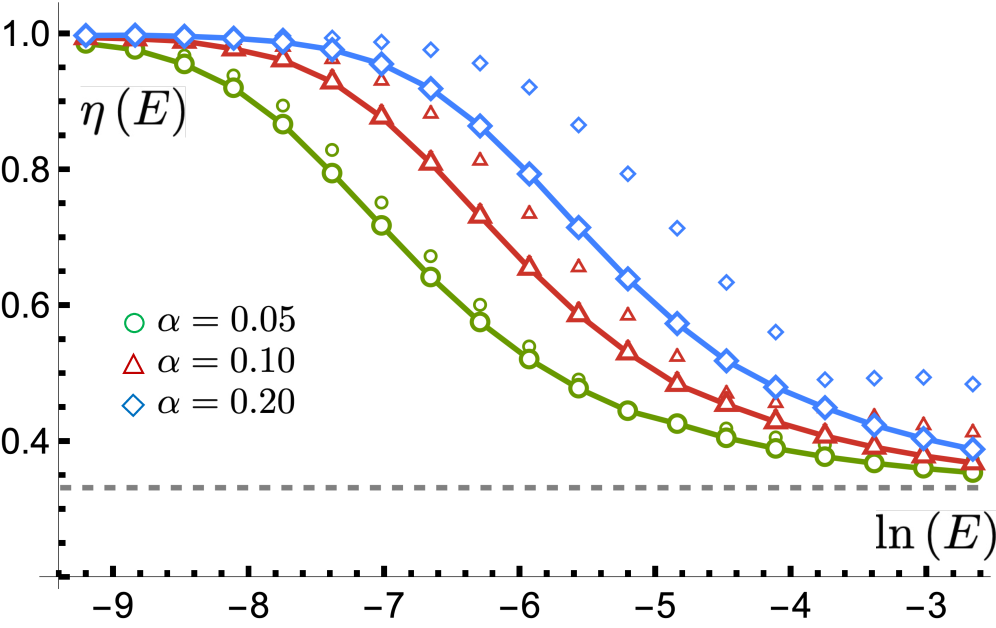
Calculations utilizing perturbation theory, RPA screening, and the polarization function demonstrate a modification of the Density of States (DOS) in bilayer graphene due to electron interactions. At low energies, the DOS exhibits a linear dependence, characterized by an exponent of $\eta = 1$ . As energy increases, the DOS transitions to a power-law dependence with an exponent of $\eta = 1/3$ . This shift in DOS behavior directly influences the material’s electronic characteristics, specifically confirming the semi-Dirac nature of the electronic spectrum, where the energy dispersion deviates from the standard Dirac cone and exhibits a modified linear dependence.

The density of states scaling <span class="katex-eq" data-katex-display="false">\eta(E)</span> exhibits weaker renormalization under the RPA screened Coulomb interaction (solid curves) compared to Hartree-Fock (unconnected markers) for interaction strengths α of 0.05, 0.10, and 0.20, with calculated values of <span class="katex-eq" data-katex-display="false">\Delta/\varepsilon_{0}</span> and <span class="katex-eq" data-katex-display="false">c/v</span> varying with α in the RPA but remaining constant at the HF level. — The density of states scaling $\eta(E)$ exhibits weaker renormalization under the RPA screened Coulomb interaction (solid curves) compared to Hartree-Fock (unconnected markers) for interaction strengths α of 0.05, 0.10, and 0.20, with calculated values of $\Delta/\varepsilon_{0}$ and $c/v$ varying with α in the RPA but remaining constant at the HF level.

Unveiling the Topology: Type-II Semi-Dirac Fermions and Their Signatures

Type-II semi-Dirac fermions emerge when two Dirac cones-relativistic, cone-shaped energy bands-merge, fundamentally altering the electronic structure of a material. This coalescence isn’t merely a structural change; it imparts a non-trivial topological characteristic known as the Berry phase. Unlike conventional materials where electrons acquire a Berry phase of zero or π, these semi-Dirac fermions exhibit a finite Berry phase, indicating a robust and protected phase that’s insensitive to small disturbances. This arises from the unique way the electron’s wavefunction changes as it moves around the Fermi surface, creating a geometric phase that dictates the material’s electronic properties. The presence of this finite Berry phase confirms the topological nature of these states and opens possibilities for utilizing them in advanced electronic devices where robustness and controlled electron behavior are paramount.

Recent material science has moved beyond theoretical prediction with the successful realization of type-II semi-Dirac fermions within layered Titanium/Vanadium Oxide Heterostructures. These artificially engineered materials demonstrate a unique electronic structure where Dirac cones coalesce, giving rise to the specific properties of these fermions. This experimental confirmation is particularly significant because it opens avenues for potential technological applications, notably in the field of spintronics. The robust nature of these states, stemming from their topological characteristics, suggests a high degree of stability and reliability, crucial for device functionality. Further research into tailoring these heterostructures promises the development of novel electronic components with enhanced performance and energy efficiency, moving beyond the limitations of conventional materials and designs.

The topological robustness of type-II semi-Dirac fermions stems from a non-zero Chern number, a mathematical quantity that characterizes the band structure’s topology and remains unchanged under continuous deformations unless a band gap closes. This inherent stability against external perturbations-such as impurities or strain-makes these materials promising candidates for spintronic devices, where reliable electron transport is paramount. Furthermore, when subjected to strong magnetic fields, the energy levels, known as Landau levels, scale differently than in conventional type-I Dirac systems; instead of the usual linear dependence on the magnetic field $nB$ , type-II semi-Dirac fermions exhibit a scaling of $[nB]^(1/(\eta+1))$ , where η represents a critical exponent characterizing the system’s low-energy behavior. This unique Landau level behavior is a direct consequence of the modified dispersion relation near the band edge and provides a key experimental signature for identifying and characterizing these novel topological states of matter.

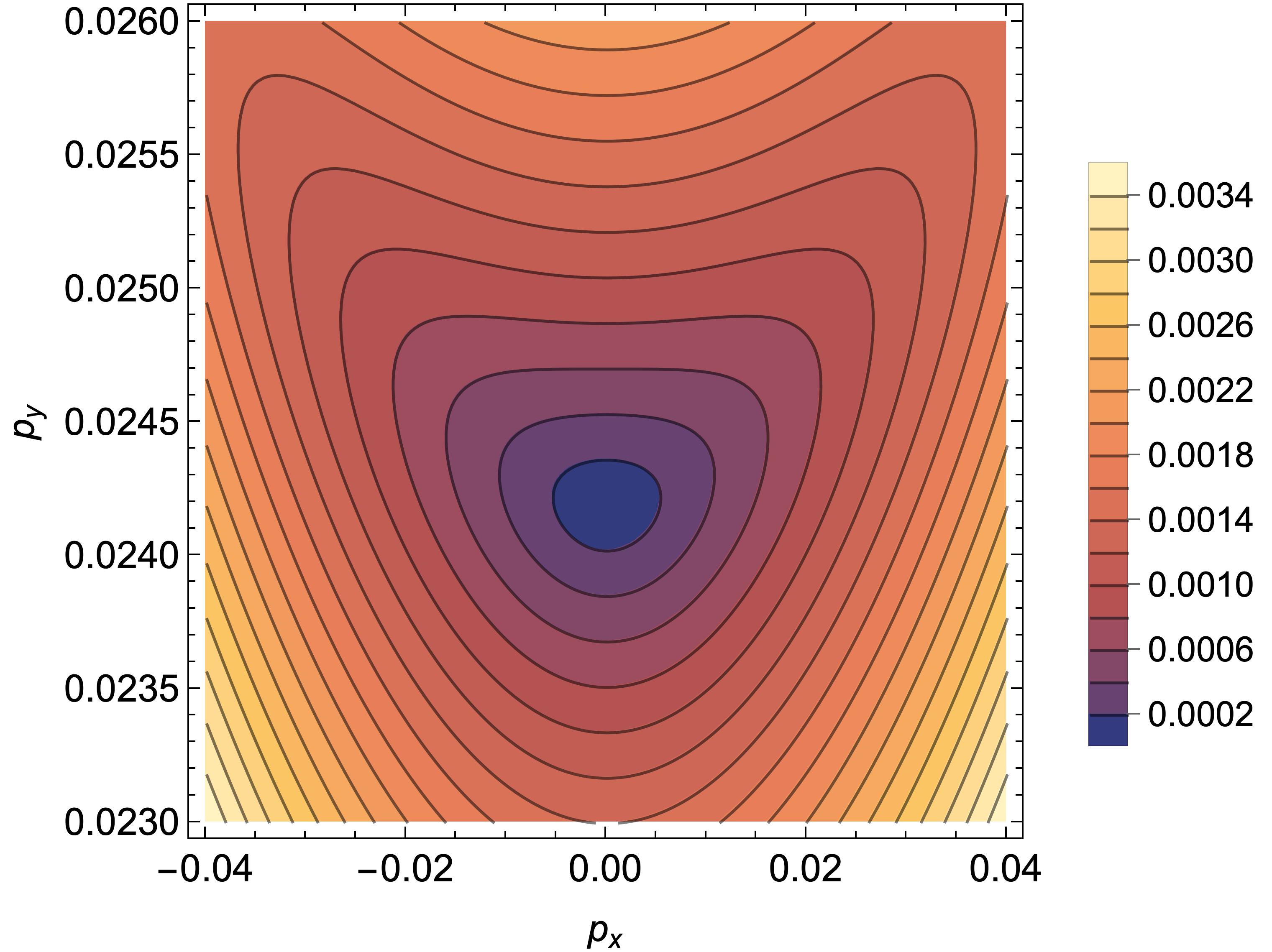
Renormalization of the Type-II semi-Dirac spectrum by the bare Coulomb interaction reveals an anisotropic Dirac cone with concave semi-Dirac behavior at higher energies, yielding values of <span class="katex-eq" data-katex-display="false">\Delta/\varepsilon_0 = 1.88/4\pi</span> and <span class="katex-eq" data-katex-display="false">c/v = 1.39/4\pi</span> using a momentum cutoff of <span class="katex-eq" data-katex-display="false">|k_{\Lambda}^{x,y}|=1.1</span>. — Renormalization of the Type-II semi-Dirac spectrum by the bare Coulomb interaction reveals an anisotropic Dirac cone with concave semi-Dirac behavior at higher energies, yielding values of $\Delta/\varepsilon_0 = 1.88/4\pi$ and $c/v = 1.39/4\pi$ using a momentum cutoff of $|k_{\Lambda}^{x,y}|=1.1$ .

Expanding the Horizon: Towards Quartic Semi-Dirac Fermions

The established semi-Dirac model, known for its unique linear-quadratic dispersion relation, finds a sophisticated extension in the realm of quartic semi-Dirac fermions. This generalization replaces the conventional quadratic term with a higher-order polynomial-specifically, a quartic function- fundamentally altering the energy-momentum relationship of these quasiparticles. This seemingly subtle shift has profound implications; by manipulating the quartic coefficient, researchers gain an unprecedented degree of control over the electronic band structure and, consequently, the material’s properties. Such control allows for the engineering of novel electronic behaviors, moving beyond the limitations inherent in simpler, quadratic-based semi-Dirac systems, and potentially unlocking advancements in areas like low-power electronics and topological quantum computation. The altered dispersion relation influences how these fermions propagate and interact, creating opportunities to design materials with tailored conductivity and responsiveness to external stimuli.

The transition to quartic semi-Dirac fermions provides a significant advancement in materials engineering, affording unprecedented manipulation of electronic behavior. By moving beyond the conventional quadratic dispersion relation, researchers gain finer control over carrier velocities and effective masses, tailoring these properties for specific applications. This expanded control isn’t merely theoretical; it directly translates to the potential for novel device functionalities, including enhanced thermoelectrics, more efficient energy harvesting, and highly sensitive sensors. The ability to engineer these quasiparticles opens doors to creating materials with custom conductivity profiles, and ultimately, devices operating with greater efficiency and performance than currently possible with conventional semiconductors.

The realization of quartic semi-Dirac fermions’ potential hinges on a deep understanding of how their topological characteristics, quantified by metrics like the Chern number, influence their dynamical conductivity-essentially, how they respond to external electromagnetic fields. Research indicates a strong correlation between these properties and measurable thermodynamic quantities; specifically, the material’s specific heat scales with temperature according to a power law of $T^{(\eta+1)}$ , where η represents a critical exponent characterizing the system’s low-energy behavior. Furthermore, the electronic compressibility-a measure of how easily the electron gas is squeezed-demonstrates a dependence on electron density, scaling as $n^{-(\eta/(\eta+1))}$ . Precisely controlling these relationships through material design and external stimuli offers a pathway to engineer novel electronic devices with tailored functionalities, potentially exceeding the limitations of conventional semiconductors.

The study of these type-II semi-Dirac fermions reveals a delicate interplay between interaction and inherent material properties, a harmony where even subtle modifications to Coulomb interactions yield measurable changes in the density of states. This echoes Thomas Hobbes’ assertion, “The life of man is solitary, poor, nasty, brutish, and short.” Though seemingly disparate, Hobbes’ observation speaks to the fundamental sensitivity of complex systems – just as a disruption to the social contract leads to chaos, a modification to the long-range interactions dramatically alters the system’s inherent characteristics and scaling behavior, as demonstrated by the renormalization group analysis and Landau level quantization detailed in the research. The interface, in this case, ‘sings’ when the delicate balance between these forces is understood.

Future Directions

The exploration of interacting type-II semi-Dirac quasiparticles, as presented, reveals a system surprisingly sensitive to even modest long-range interactions. While the renormalization group analysis and random phase approximation calculations offer a coherent picture, they necessarily rely on approximations. The true elegance of this system-the harmonious balance between its anisotropic Dirac cone and Coulombic effects-remains partially obscured. A more complete treatment would necessitate going beyond perturbative schemes, perhaps leveraging numerical techniques to map out the full phase diagram and identify any emergent, strongly correlated states.

The tunable density of states, a central finding, hints at the possibility of engineering materials with tailored electronic properties. However, realizing this potential requires bridging the gap between theoretical models and actual material systems. Identifying or creating materials that host these type-II semi-Dirac fermions-and that simultaneously allow for precise control over Coulomb interactions-presents a significant challenge. The question isn’t simply can these properties be manipulated, but how can they be expressed in a physically realizable, robust manner?

Ultimately, this work underscores a recurring theme in condensed matter physics: simplicity is a dangerous illusion. The initial promise of semi-Dirac fermions-a system ostensibly less complex than its Dirac counterpart-is quickly tempered by the reality of many-body interactions. The task now falls to future investigations to disentangle these complexities and reveal the underlying principles governing this fascinating, and stubbornly nuanced, state of matter.

Original article: https://arxiv.org/pdf/2601.21098.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/