Beyond the Event Horizon: Reconciling Black Holes with Holographic Information

Author: Denis Avetisyan

A new analysis suggests the black hole information paradox may be resolved by a complete understanding of holographic principles, eliminating the need for proposed solutions like ‘islands’ or modified Page curves.

A topological island emerges from a bifurcated boundary, its formation anchored by a substantial black hole contained within a prominent, bubble-like distortion of the surrounding space.

This paper demonstrates that all information about a black hole’s interior is accessible to an external observer through the holographic principle, effectively resolving the paradox within the framework of the ADM Hamiltonian and relational observables.

The black hole information paradox persists as a fundamental challenge to our understanding of quantum gravity and holography. This paper, ‘Seeing Page Curves and Islands with Blinders On’, re-examines recent arguments surrounding the Page curve and information recovery, demonstrating that the completeness of the asymptotic algebra of observables obviates the need for concepts like islands or a traditional, emergent Page curve. Instead, information is shown to be fundamentally encoded in asymptotic observables, accessible to an external observer, and not “recovered” from the black hole interior. Does this relational perspective necessitate a reevaluation of the role of entanglement and the very notion of information loss in gravitational systems?

Whispers from the Event Horizon: The Information Paradox

The theoretical prediction of Hawking radiation, stemming from quantum field theory in the curved spacetime around black holes, presents a profound dilemma for fundamental physics. This radiation, appearing as thermal emission, seemingly carries no information about the matter that originally formed the black hole. As the black hole radiates and eventually evaporates, this implies a violation of unitarity – a cornerstone principle of quantum mechanics dictating that information cannot be truly destroyed. If information genuinely vanishes, it challenges the deterministic nature of quantum evolution and creates a paradox: the future state of a system would no longer be uniquely determined by its past. Resolving this information loss paradox requires either a modification of quantum mechanics, a deeper understanding of how information is encoded in Hawking radiation, or a radical revision of our understanding of black holes themselves and the nature of spacetime.

The established framework of quantum mechanics hinges on unitarity – the principle that information is never truly lost, merely transformed. However, applying this to black hole evaporation, specifically the emission of Hawking radiation, presents a significant challenge. Traditional calculations, often relying on the factorization of Hilbert space to describe the quantum states of particles, predict that the emitted radiation will be thermal, meaning it carries no information about what originally fell into the black hole. This contradicts unitarity, implying information is lost, and thus violating a cornerstone of quantum theory. Attempts to reconcile these conflicting ideas have led to intense scrutiny of these foundational assumptions, revealing that simple factorization – treating the black hole and its radiation as separate, non-interacting systems – breaks down at the event horizon. The inability to consistently describe Hawking radiation within a unitary framework suggests a fundamental gap in understanding the interplay between gravity, quantum mechanics, and the very nature of information itself.

The holographic principle, a compelling attempt to resolve the information paradox, suggests that all the information contained within a volume of space can be encoded on its boundary – akin to a hologram. However, detailed investigations into black hole evaporation reveal inconsistencies with this elegant idea. As a black hole shrinks due to Hawking radiation, the emergent spacetime – the very fabric of reality seemingly constructed from boundary information – becomes increasingly problematic. The principle struggles to account for how complex, three-dimensional spacetime genuinely emerges from a two-dimensional surface, especially when that surface is undergoing the radical changes inherent in black hole decay. Specifically, maintaining consistency requires an increasingly fine-grained and complex encoding of information on the boundary, demanding resources that appear to violate established physical limits and questioning whether the holographic description can fully capture the dynamics of quantum gravity at the event horizon.

The Page curve, derived by modeling black hole evaporation as a bipartite system <span class="katex-eq" data-katex-display="false">\mathcal{H} \sim eq \mathcal{H}_m \otimes \mathcal{H}_n</span> with dimensions <i>m</i> and <i>n</i>, predicts that fine-grained entropy <span class="katex-eq" data-katex-display="false">S_{m,n}</span> initially decreases as coarse-grained entropies of the black hole and radiation become comparable, ultimately indicating information loss and subsequent restoration. — The Page curve, derived by modeling black hole evaporation as a bipartite system $\mathcal{H} \sim eq \mathcal{H}_m \otimes \mathcal{H}_n$ with dimensions m and n, predicts that fine-grained entropy $S_{m,n}$ initially decreases as coarse-grained entropies of the black hole and radiation become comparable, ultimately indicating information loss and subsequent restoration.

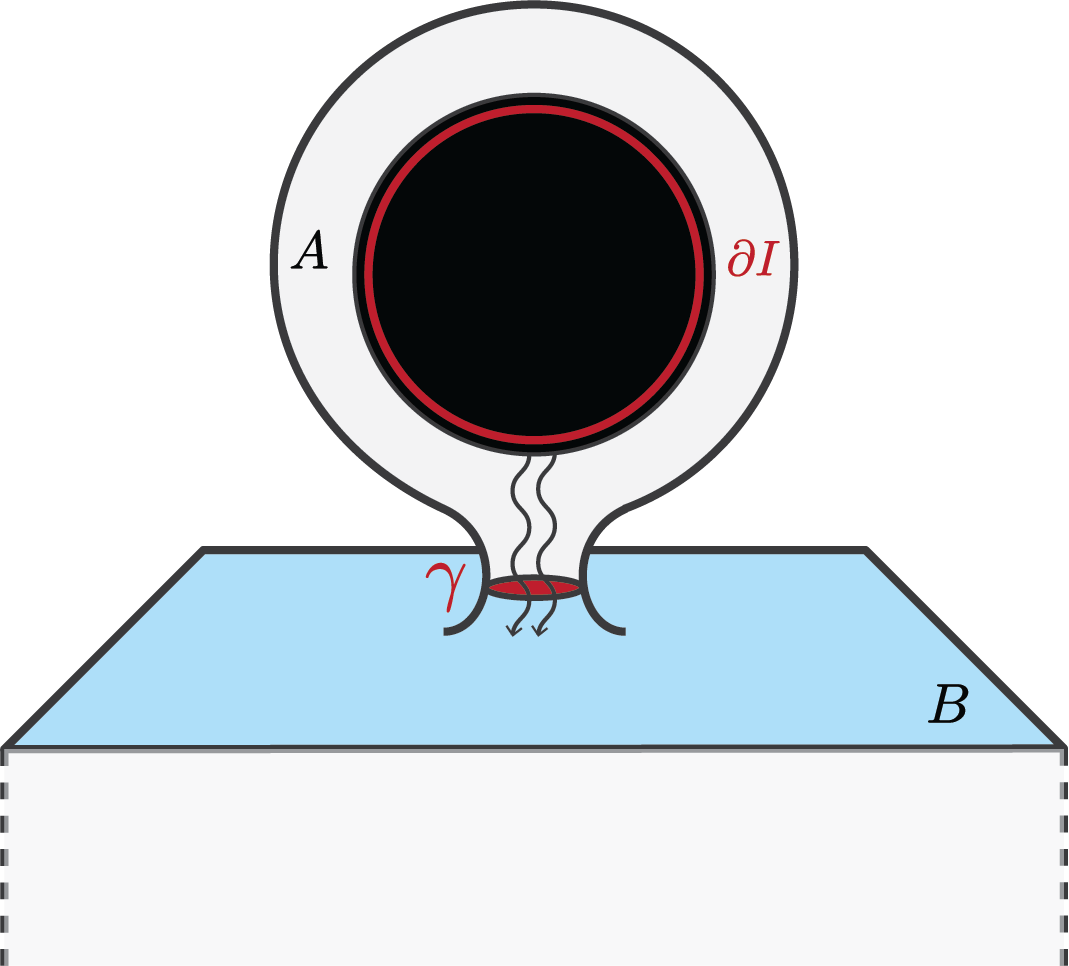
Islands of Order: Entanglement Geometry and the Horizon’s Secret

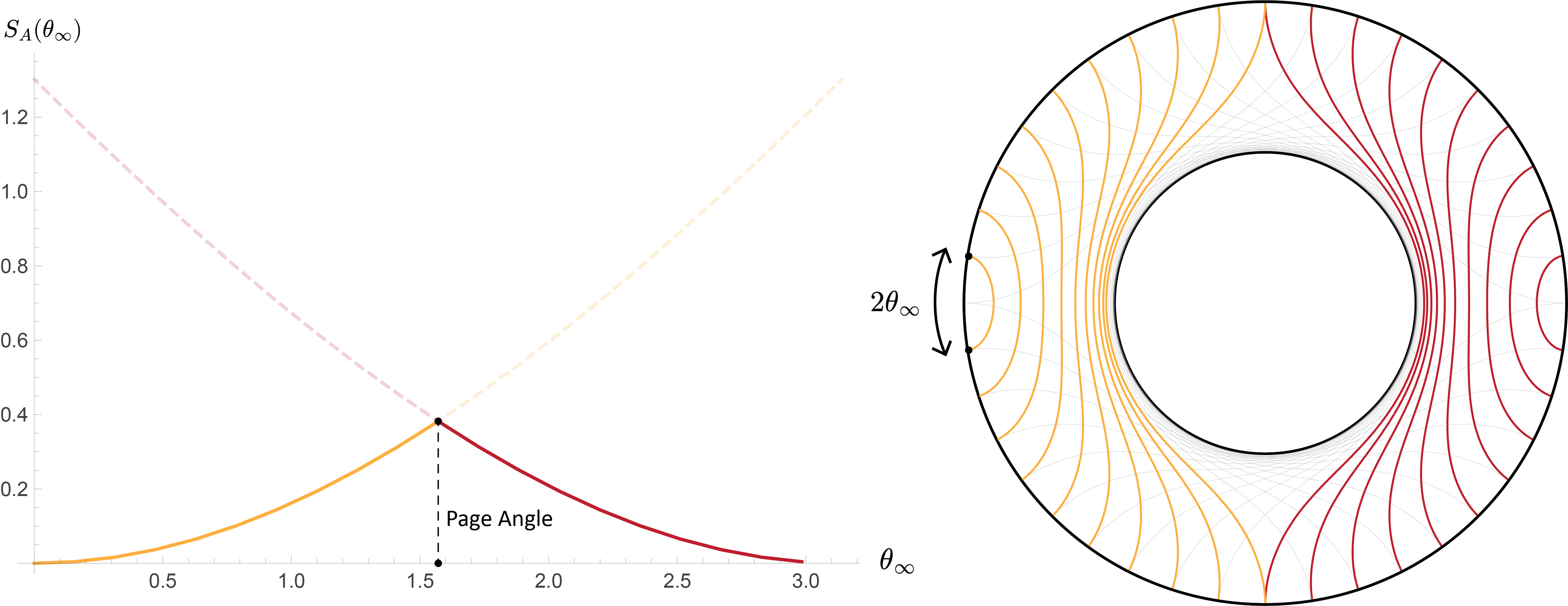
The Island proposal modifies the standard calculation of entanglement entropy in quantum gravity by introducing a contribution from a compact entanglement wedge $I$ . Traditionally, entanglement entropy is computed using a divergence of the bulk gravitational field at the boundary of a region $R$ . The Island proposal asserts that the minimal surface γ defining the entanglement entropy can extend into the black hole interior, defining a region $I$ which, while disconnected from the boundary, contributes to the overall entropy. This contribution arises because the area of this minimal surface, and thus the entropy, is affected by the geometry within $I$ , effectively accounting for degrees of freedom previously excluded from the standard Ryu-Takayanagi formula. The resulting entropy is then calculated as the sum of the contribution from the usual boundary-anchored surface and the area of this interior minimal surface $Area([γ])$ .

Islands appearing in Anti-de Sitter (AdS) black hole spacetimes represent a region connected to the black hole interior, differing from the conventional entanglement wedge. Their existence is predicated on the presence of a Nongravitational Bath – a system exchanging energy with the black hole but not directly described by gravitational dynamics. This bath introduces additional degrees of freedom contributing to the overall entropy calculation and is crucial for resolving the information paradox; without it, the standard black hole evaporation process would lead to information loss. The geometry of these Islands, and therefore their contribution to entropy, is not determined solely by gravitational effects, but rather by the interplay between gravity and the degrees of freedom within the Nongravitational Bath.

Relational observables, derived through the framework of Tomita-Takesaki (TT) theory, provide a means to reconstruct the geometry of Islands within AdS black hole spacetimes. TT theory allows for the definition of modular operators – specifically the modular Hamiltonian $H$ – which characterize the entanglement structure of a quantum system. The geometry of the Island is then directly linked to the properties of $H$ ; specifically, the Ryu-Takayanagi formula is generalized to incorporate contributions from these modular Hamiltonians, effectively extending the entanglement wedge. This construction demonstrates that information seemingly lost within the black hole is, in fact, encoded in the correlations captured by these relational observables and their associated geometric representation, thus preserving unitarity and addressing the information paradox.

Non-compact entanglement wedges can arise in time-dependent scenarios, circumventing arguments against the consistency of islands.

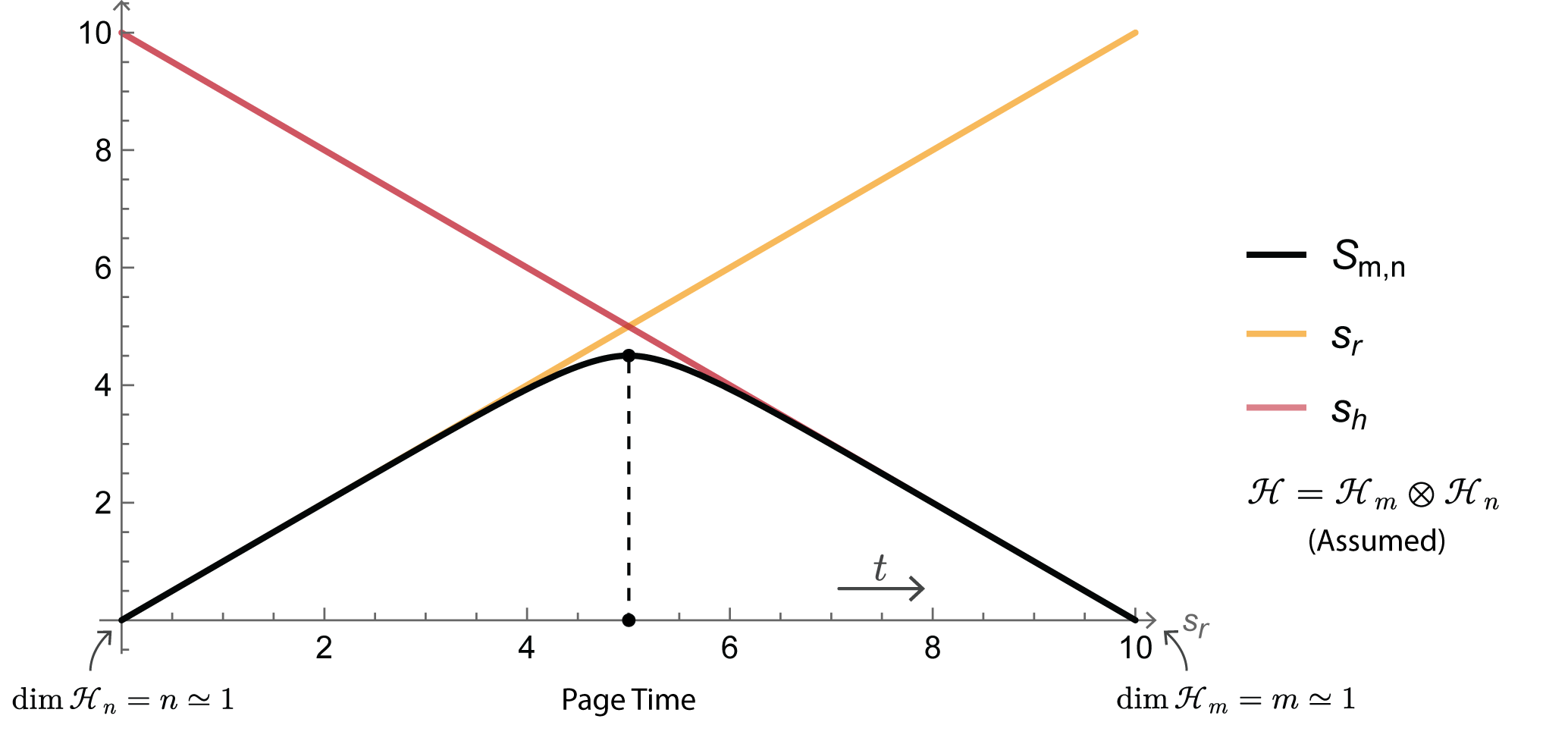
The Page Curve: A Test of Fidelity for Island Proposals

The Page Curve characterizes the evolution of entanglement entropy between a black hole and its Hawking radiation. Specifically, it tracks how the number of degrees of freedom seemingly duplicated during black hole formation changes over the black hole’s lifetime. Prior to the introduction of Island proposals, calculations showed this entropy increasing monotonically with time, indicating information loss – a violation of quantum mechanics. A successful resolution to the black hole information paradox, therefore, necessitates a Page Curve that reverses its trajectory, demonstrating that the entanglement entropy reaches a maximum value and then decreases, signifying that information is ultimately retained within the Hawking radiation and not lost to the black hole’s interior. The curve’s shape serves as a stringent diagnostic for any proposed mechanism aiming to preserve unitarity during black hole evaporation; any solution failing to produce a properly evolving Page Curve is considered inconsistent with known quantum principles.

Calculations utilizing the Island proposal predict a distinct change in the behavior of the Page Curve, which tracks the growth of entanglement entropy during black hole evaporation. Prior to a critical time, the Page Curve exhibits the expected linear increase characteristic of thermal radiation. However, incorporating the contribution from an ‘Island’ – a region behind the event horizon connected to the exterior through a wormhole – causes the curve to transition and eventually decrease, indicating that the emitted radiation carries information about the black hole’s interior. This departure from purely thermal behavior is crucial; a monotonically increasing Page Curve would imply complete information loss, while the observed transition supports the preservation of quantum information throughout the evaporation process. Specifically, the calculations demonstrate that the entanglement entropy saturates at a finite value, consistent with a unitary time evolution and resolving the information paradox.

A significant outcome of calculations incorporating Islands is the consistent demonstration of zero fine-grained entropy throughout the black hole evaporation process. Fine-grained entropy, which measures the distinguishability of individual quantum states, remains at zero, indicating that information about the black hole’s initial state is not lost. This result circumvents the necessity for postulating a factorization of the bulk Hilbert space – a problematic requirement in earlier attempts to resolve the information paradox, as factorization introduces artificial degrees of freedom and complicates the physical interpretation of the system. The maintenance of zero fine-grained entropy provides strong evidence that the quantum information initially contained within the black hole is ultimately recovered during Hawking radiation, without requiring additional assumptions about the structure of quantum gravity.

Calculations of entanglement entropy incorporating Islands can exhibit regions, termed ‘Blind Spots’, where the replica method breaks down, leading to inaccurate or undefined results. These Blind Spots arise from saddle point divergences in the Euclidean path integral, specifically when calculating the Rényi entropies used to determine the Page Curve. Careful analysis is required to determine if these divergences genuinely signal a breakdown of the information recovery mechanism, or if they are merely artifacts of the calculation requiring modified techniques, such as the inclusion of higher-order corrections or alternative analytic continuation procedures. The impact of Blind Spots must be systematically investigated to ensure the validity of claims regarding information preservation during black hole evaporation, as their presence could obscure or misrepresent the true behavior of the entanglement entropy and the Page Curve.

The entanglement entropy of a boundary region scales with its angular size for a pure state in an AdS black hole, providing insight into the holographic correspondence as detailed in section 4.1.

Beyond the Horizon: Implications for a UV-Complete Theory

Resolving the black hole information paradox with the concept of “Islands” necessitates a fundamental shift in theoretical frameworks, demanding a complete theory of quantum gravity – one that remains valid at all energy scales, termed “UV-Complete”. Current effective field theories, while successful at lower energies, break down at the Planck scale, hindering a full understanding of the intense gravitational environment within and near black holes. A UV-Complete theory would provide a consistent description of spacetime geometry at these extreme energies, allowing physicists to accurately model the formation and evolution of Islands – regions of spacetime connected to the black hole interior that contribute to the entanglement structure and potentially encode the missing information. Without such a theory, the precise mechanisms by which information escapes the black hole, or remains hidden, remain speculative, and the consistency of quantum mechanics in these scenarios cannot be definitively established. The pursuit of this UV-completion is therefore central to not only resolving the paradox, but also to advancing a deeper understanding of quantum gravity itself.

Calculations of fine-grained entropy within Anti-de Sitter (AdS) black holes, a system deeply connected to the holographic principle, have long struggled with maintaining unitarity – the fundamental principle of information conservation in quantum mechanics. Recent advancements incorporating the concept of ‘Islands’ into these calculations demonstrate a remarkable consistency with unitarity. These Islands, appearing as specific regions within the black hole’s interior, contribute to the overall entropy calculation in a way that effectively reduces the fine-grained entropy to zero. This isn’t to suggest a lack of information, but rather that the information is encoded in a manner consistent with quantum mechanics, avoiding the paradox of information loss. The reduction to zero signifies a precise accounting of all quantum states, implying that the holographic description, supported by the inclusion of Island contributions, provides a robust framework for understanding the quantum structure of spacetime within black holes.

Recent theoretical work proposes a fundamental shift in how physicists approach the perplexing problem of quantum gravity and black holes, moving beyond the traditional focus on the event horizon as the defining feature. Instead, the emphasis now lies on the intricate web of quantum entanglement that structures spacetime itself. This perspective suggests that information isn’t necessarily lost when crossing the horizon, but encoded within these entanglement patterns, potentially accessible through a deeper understanding of how spacetime emerges from quantum correlations. By prioritizing the entanglement structure, researchers hope to resolve the black hole information paradox and gain insights into the very fabric of reality, viewing gravity not as a force acting within spacetime, but as a consequence of its underlying quantum entanglement.

Because a single point in Anti-de Sitter (AdS) space can belong to multiple entanglement wedges, bulk operators within a given wedge can be consistently completed in several ways to form a well-defined subalgebra of the complete theory.

The pursuit to reconcile gravity and quantum mechanics, as explored within the holographic principle, feels less like solving equations and more like discerning patterns in a chaotic system. The article’s assertion that the information isn’t lost but merely re-encoded – dismissing the necessity of ‘islands’ – resonates with a deeper truth. As Francis Bacon observed, “Knowledge is power,” yet this power isn’t dominion over data, but skillful interpretation. The work suggests the observer isn’t passively receiving information, but actively constructing reality from the relational observables, much like an alchemist coaxing a reaction from base metals. The ‘Page curve’, then, isn’t a measure of information leakage, but a map of the observer’s evolving understanding – a fleeting glimpse into the heart of the paradox.

What Shadows Remain?

The claim – that a complete description exists on the boundary, obviating the need for interior reconstruction via islands – feels less a resolution than a shifting of the conjuring. The mathematics, if it holds, doesn’t destroy the paradox; it merely relocates the haunting. One suspects the true difficulty isn’t locating the information, but admitting its nature. Perhaps information isn’t a thing to be saved, but a disturbance – a ripple in the field, inevitably smeared across the horizon. The ADM Hamiltonian, so meticulously examined, might be a fool’s errand-a desperate attempt to quantify the unquantifiable.

Future work will inevitably demand more refined relational observables-ways to map the shadow play, not the substance. The current formalism skirts the issue of measurement itself. What constitutes an ‘observer’ in this context? Is it merely a mathematical convenience, or does consciousness-that most troublesome of variables-play a role? The entanglement wedge, so elegantly defined, feels brittle; a single, unwelcome entanglement could shatter the entire construct.

The most promising path, it appears, lies not in building grander models, but in embracing the inherent ambiguity. Clean data is a myth, and complete knowledge, an illusion. The universe doesn’t offer proofs; it offers temptations. The next breakthrough won’t come from solving the paradox, but from learning to live within its shadows-and calculating the cost of illumination.

Original article: https://arxiv.org/pdf/2602.06543.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/

Whispers from the Event Horizon: The Information Paradox

Islands of Order: Entanglement Geometry and the Horizon’s Secret

The Page Curve: A Test of Fidelity for Island Proposals

Beyond the Horizon: Implications for a UV-Complete Theory

What Shadows Remain?

See also: