Beyond the Quantum Wave: Reclaiming Particle Trajectories

Author: Denis Avetisyan

A new perspective on quantum mechanics proposes resolving long-standing paradoxes by explicitly modeling the paths of individual particles.

The study demonstrates that a quantum particle’s state-whether its ground state or a coherent state with energy $3\hbar\omega$-manifests distinct probability distributions for its position, highlighting the fundamental differences in how these states evolve within classical motion.

This review explores Quantum Analytical Mechanics, a formalism extending standard quantum mechanics through stochastic dynamics and hidden variables to address the measurement problem and provide a more complete physical picture.

The completeness of quantum mechanics and the enduring measurement problem present a fundamental tension in our understanding of physical reality. This paper introduces ‘Quantum Analytical Mechanics: Quantum Mechanics with Hidden Variables’, a framework extending standard quantum formalism via stochastic trajectories in configuration space. By deriving equations of motion for particle coordinates and orientations, this approach describes measurement not as an instantaneous collapse, but as a dynamical physical process governed by hidden variables. Could such a completion offer a more intuitive and complete description of quantum phenomena, bridging the gap between theory and observation?

Beyond Static Description: Charting a Dynamic Quantum Reality

Conventional Hilbert space quantum mechanics, despite its predictive power, fundamentally describes quantum states as existing within a fixed mathematical space, offering a snapshot rather than a continuous unfolding. While the Schrödinger equation governs the time evolution of these states, it does so by altering the wavefunction within this static framework, not by charting a dynamic path for individual particles. This approach, though remarkably effective for many scenarios, presents limitations when considering processes that demand a detailed understanding of particle trajectories – particularly in the realm of quantum measurement. The theory excels at predicting probabilities, but provides no inherent mechanism for describing how a quantum system transitions from a superposition of states to a definite outcome, leaving a gap in understanding the actual dynamic evolution of the system itself. This static perspective necessitates alternative theoretical approaches capable of resolving this dynamic incompleteness and providing a richer, more intuitive picture of quantum reality.

The limitations of a static quantum description become acutely apparent when attempting to model complex phenomena beyond simple, isolated systems. Traditional Hilbert space mechanics struggles to accurately represent measurement processes, where the act of observation fundamentally alters the quantum state; the resulting wave function collapse isn’t a dynamic evolution within the established framework, but rather an abrupt shift. Similarly, particles existing in non-equilibrium states – those not at thermal equilibrium with their surroundings – exhibit behaviors that defy easy characterization by static wave functions. These systems, crucial to understanding areas like quantum thermodynamics and many-body physics, demand a description that captures the continuous, dynamic evolution of quantum states, not merely their initial and final configurations. Consequently, progress in these fields is hampered by the inability to consistently track the trajectories and interactions of individual quantum entities as they move through phase space, necessitating a more robust and dynamic quantum theory.

A comprehensive quantum theory necessitates the description of individual particle trajectories and their evolution, moving beyond the static framework of traditional Hilbert space mechanics. Current approaches often struggle to reconcile theoretical predictions with observed quantum behavior, particularly during measurement events where the wave function collapses. Recent investigations demonstrate that by tracking the precise path of particles, a dynamically complete theory can resolve the measurement problem – the ambiguity surrounding how definite outcomes arise from probabilistic quantum states. This trajectory-based approach doesn’t require a priori assumptions about collapse; instead, it reveals that measurement outcomes are determined by the specific path each particle takes, aligning theoretical models with empirical observation and offering a potentially more intuitive understanding of quantum reality. The ability to consistently predict outcomes based on these trajectories suggests a fundamental connection between particle dynamics and the emergence of classical behavior from the quantum realm.

Nelson’s Stochastic Mechanics: A Foundation for Dynamic Quantum Description

Nelson’s Stochastic Mechanics posits that quantum particles are not governed by deterministic trajectories, but rather by diffusion processes described by a stochastic differential equation. This equation, formally expressed as $dx_i = \sqrt{2S_i(x,t)} \, dW_i(t)$, defines the particle’s position $x_i$ as a function of a Wiener process $W_i(t)$ and a time-dependent diffusion coefficient $S_i(x,t)$. The $S_i(x,t)$ term, derived from the quantum potential, dictates the rate of diffusion and is unique to each particle and its environment. Unlike standard Brownian motion, the diffusion is guided by this potential, ensuring that the statistical behavior reproduces the predictions of quantum mechanics, specifically the Schrödinger equation. Consequently, particle trajectories are irregular but statistically well-defined, offering a particle-based interpretation of wave function evolution.

Nelson’s Stochastic Mechanics posits that quantum particles are not governed by deterministic equations of motion, but rather by diffusion processes described by a stochastic differential equation. This formulation inherently defines a trajectory for each particle, even between measurements, circumventing the traditional issue of undefined particle paths in standard quantum mechanics. The diffusion is guided by a potential that incorporates both the classical potential energy and a “quantum potential” derived from the wavefunction’s curvature. Consequently, the measurement problem is addressed because the particle always has a definite, albeit probabilistically determined, trajectory, and measurement simply reveals the particle’s position along that pre-existing path; the act of measurement doesn’t collapse the wavefunction but rather reveals a value already determined by the stochastic process. This contrasts with the Copenhagen interpretation, where properties are undefined until measured.

The Madelung equations, derived from the Schrödinger equation through a transformation involving the complex-valued wave function $\Psi = \sqrt{\rho}e^{iS/\hbar}$, explicitly connect quantum and classical descriptions of particle behavior. These equations consist of a continuity equation, $\partial \rho / \partial t + \nabla \cdot (\rho v) = 0$, describing the conservation of probability density $\rho$, and a Hamiltonian-Jacobi equation, $\partial S / \partial t + \frac{1}{2m}(\nabla S)^2 + V = 0$, defining an effective potential $V$ and velocity field $v = \frac{1}{m}\nabla S$. This formulation allows for the treatment of quantum phenomena in terms of classical-like trajectories guided by the quantum potential, thereby demonstrating that the Schrödinger equation can be viewed as a fluid dynamic equation governing the evolution of a quantum fluid with density $\rho$ and velocity field $v$.

Extending the Framework: Quantum Analytical Mechanics and Empirical Validation

Quantum Analytical Mechanics builds upon Nelson’s Stochastic Mechanics by offering a more comprehensive framework for modeling complex quantum systems. While Nelson’s approach provides a stochastic description of quantum phenomena, Quantum Analytical Mechanics extends this to specifically address systems such as the Stern-Gerlach experiment, where spin-dependent forces act on particles, and to fully characterize particle behavior within configuration space. This expansion allows for detailed analysis of quantum trajectories and correlations not readily accessible in simpler stochastic models, facilitating the investigation of phenomena involving spatially distributed probabilities and dynamic interactions. The framework supports the simulation and prediction of particle behavior in complex potentials and electromagnetic fields, providing a tool for analyzing and interpreting quantum measurements.

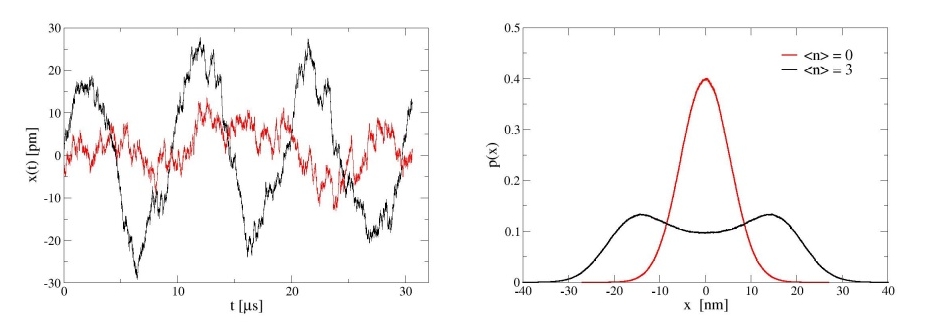
Quantum Analytical Mechanics employs stochastic processes to model particle movement, enabling the examination of individual quantum trajectories and the statistical relationships between them. This approach deviates from traditional quantum mechanics by providing a dynamic, rather than probabilistic, description of particle behavior. Recent levitation experiments have validated the framework, achieving a temporal resolution of 32 nanoseconds in tracking particle dynamics. This resolution allows for the observation of subtle fluctuations in particle paths and the quantification of correlations between successive positions, providing a more granular understanding of quantum phenomena than previously possible. The methodology allows for the calculation of transition probabilities and the reconstruction of particle histories within the configuration space.

Quantum Analytical Mechanics, leveraging the Bopp-Haag picture, enables the dynamic modeling of rotating charged particles and their associated magnetic moments. This approach circumvents the traditional issues with Zitterbewegung by incorporating internal degrees of freedom that account for rapid, intrinsic motion. Initial beam analysis utilizing this framework has demonstrated a measurable particle width of 150 μm, indicating the spatial extent of the dynamically rotating charge distribution. The Bopp-Haag picture allows for a consistent description of the particle’s spin and orbital angular momentum within the stochastic framework, facilitating the calculation of time-dependent magnetic dipole moments and their interaction with external fields.

Hidden Variables and the Quest for a Complete Quantum Description

Quantum Analytical Mechanics emerges as a sophisticated extension of hidden variable theory, directly confronting the perplexing issue of non-locality revealed by Bell’s Theorem. While conventional quantum mechanics describes correlations between particles as instantaneous regardless of distance, seemingly violating the speed of light, this framework attempts to restore a degree of locality by positing the existence of ‘hidden’ variables that predetermine particle behavior. However, fully resolving the implications of Bell’s Theorem remains a considerable challenge; even with these hidden variables, any attempt to explain quantum correlations through purely local mechanisms inevitably necessitates abandoning either realism – the idea that physical properties exist independently of observation – or locality itself. Therefore, Quantum Analytical Mechanics, though offering a potential pathway around some of the more counterintuitive aspects of quantum entanglement, still requires careful consideration of the fundamental trade-offs inherent in reconciling quantum theory with our classical intuitions about space, time, and causality.

Bohmian Mechanics offers a distinct pathway within hidden variable theories by positing that particles possess definite positions at all times, guided by a ‘quantum potential’ derived from the wavefunction. Unlike interpretations suggesting inherent randomness, this approach proposes a deterministic evolution of particle trajectories, even while reproducing all the statistical predictions of standard quantum mechanics. This framework reimagines the wavefunction not as solely describing probability, but as a ‘pilot wave’ influencing particle motion – a concept that directly addresses the non-locality revealed by Bell’s Theorem without necessitating instantaneous action at a distance. While mathematically complex, Bohmian Mechanics provides a compelling, albeit controversial, alternative to the Copenhagen interpretation, offering a potentially more intuitive picture of quantum reality where particles follow well-defined paths shaped by the quantum environment, offering a means to explore the implications of hidden variables within a fully developed analytical framework.

The adoption of Quantum Analytical Mechanics as a foundational framework enables researchers to probe the intricacies of quantum correlations and entanglement with unprecedented detail. By extending hidden variable theories, this approach moves beyond simply accounting for these phenomena to actively investigating the underlying mechanisms that give rise to them. This deeper investigation isn’t merely a refinement of existing quantum models; it directly addresses questions about the nature of reality itself, examining whether quantum entanglement represents a fundamental connection between particles that transcends spatial separation. Consequently, studies within this framework seek to determine if the observed correlations stem from pre-existing, local properties – hidden variables – or if they reflect a non-local reality where distant particles are intrinsically linked, potentially reshaping our understanding of causality and information transfer at the quantum level.

Toward a Complete Quantum Theory: Modeling Complex Systems and Future Directions

Quantum Analytical Mechanics presents a novel approach to understanding intricate quantum systems, moving beyond traditional methods often limited by complexity. This framework effectively models systems like the Quantum Harmonic Oscillator – a fundamental concept in physics describing vibrations at the quantum level – by leveraging the mathematical elegance of Coherent States. These states, resembling classical wave-like behavior, provide a remarkably accurate and simplified description of particle behavior, allowing physicists to predict and analyze quantum phenomena with greater ease. By representing quantum states as continuous variables, rather than discrete ones, Quantum Analytical Mechanics offers a powerful toolkit for tackling previously intractable problems in quantum mechanics, potentially revolutionizing fields reliant on precise quantum modeling, such as the development of advanced sensors and the design of next-generation quantum computers. The approach offers a path toward simulating and controlling quantum systems with unprecedented accuracy, promising breakthroughs in materials science and fundamental physics.

The principles underpinning Quantum Analytical Mechanics extend beyond theoretical exploration, offering tangible advancements across multiple technological frontiers. In quantum computing, a deeper understanding of coherent states and dynamically complete theories could facilitate the creation of more stable and scalable qubits – the fundamental units of quantum information. Simultaneously, quantum sensing benefits from this approach through the development of devices with unprecedented precision, capable of measuring subtle changes in physical quantities like magnetic fields or gravity. Perhaps most significantly, the ability to accurately model complex quantum systems is proving invaluable in the design and discovery of novel quantum materials – substances exhibiting exotic properties with potential applications ranging from superconductivity to advanced energy storage, promising a revolution in materials science and engineering.

The advancement of quantum technologies hinges on the development of dynamically complete quantum theories, frameworks capable of accurately predicting the time evolution of any quantum state. Current theoretical approaches, while successful in many scenarios, often rely on approximations or specific conditions, limiting their applicability to truly complex systems. Pursuing dynamically complete descriptions – those governed by a minimal set of parameters and free from inherent limitations – promises to overcome these hurdles, enabling the design of more robust quantum computers, ultra-sensitive quantum sensors, and novel materials with tailored quantum properties. Such theories aren’t merely about improving existing technology; they represent a fundamental step towards a deeper comprehension of the quantum realm, potentially revealing unforeseen phenomena and challenging established paradigms in physics. The pursuit of these complete theories demands ongoing investigation into the mathematical structures underpinning quantum mechanics, alongside innovative experimental techniques to validate and refine theoretical predictions.

The pursuit of a complete quantum mechanical description, as detailed in this work, necessitates a departure from purely probabilistic interpretations. The author posits that incorporating stochastic dynamics and explicitly defined particle trajectories offers a pathway toward resolving the measurement problem-a persistent challenge in the field. This approach aligns with a broader philosophical inclination toward seeking underlying deterministic mechanisms, even within seemingly random systems. As Louis de Broglie stated, “It is tempting to believe that all of physics can be reduced to the study of trajectories.” The paper’s emphasis on defining these trajectories-even if probabilistic-reflects a dedication to completeness and a rejection of interpretations that simply accept the limitations of the Hilbert space formalism without further investigation. If these trajectories cannot be consistently replicated through rigorous analysis, the underlying model remains incomplete.

What’s Next?

The persistent appeal of completing quantum mechanics through hidden variables – or, more precisely, stochastic dynamics beyond the Hilbert space – isn’t a search for simpler answers, but for better questions. The formalism presented here, and variations like Nelson’s mechanics, offer a mathematically consistent path for describing quantum trajectories, but a trajectory isn’t explanation. The real challenge lies not in calculating where a particle might be, but in understanding why that particular trajectory is realized, given the inherent probabilistic nature. Anything confirming expectations needs a second look.

Future work must confront the unsettling possibility that the “measurement problem” isn’t a failing of the quantum description itself, but a misapplication of classical intuition. To assume a definite outcome prior to interaction is a particularly insidious form of prejudice. A hypothesis isn’t belief – it’s structured doubt. Therefore, rigorous investigation into the ontological status of these trajectories-are they merely computational aids, or do they reflect a deeper reality?-remains paramount.

Ultimately, the value of quantum analytical mechanics may not be in providing a “complete” quantum theory-an ambition perhaps predicated on a flawed notion of completeness-but in forcing a more honest appraisal of what constitutes a physical explanation. The field needs less confirmation and more relentless attempts at falsification. The absence of paradox, after all, is not evidence of truth.

Original article: https://arxiv.org/pdf/2511.21435.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/