Author: Denis Avetisyan
This review explores how extending quantum field theory to include non-Hermitian effects impacts the behavior of electron-positron scattering at finite temperatures.
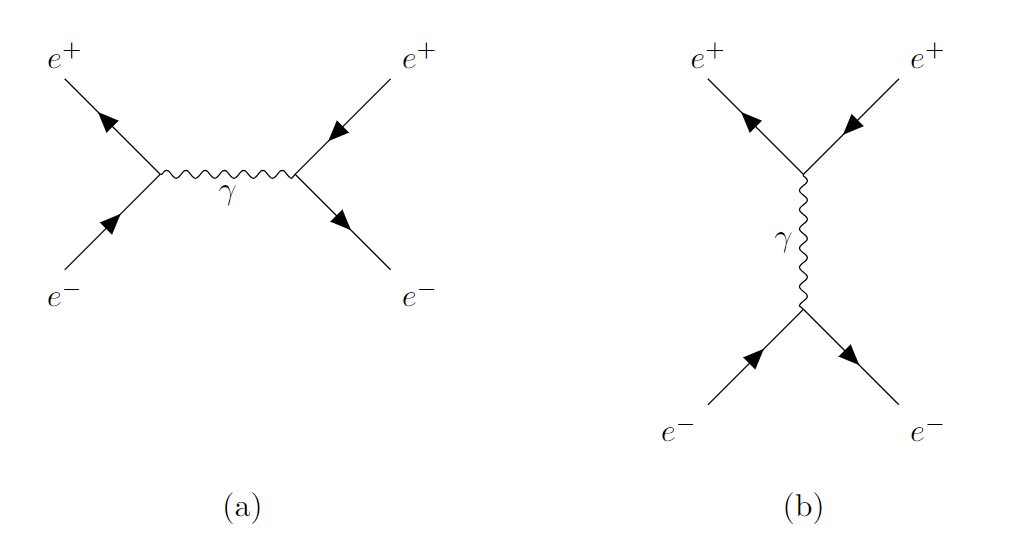
The study investigates thermal Bhabha scattering under non-Hermitian conditions, establishing limits on axial coupling parameters and analyzing the role of exceptional points.
Conventional quantum field theory relies on Hermitian operators to ensure physically realistic observables, yet extensions beyond this strict requirement offer novel theoretical landscapes. This work, ‘Thermal Bhabha scattering under the influence of non-hermiticity effects’, investigates Bhabha scattering within a non-Hermitian framework employing PT-symmetry and finite temperature effects calculated via Thermofield Dynamics. We derive the thermal differential cross section and establish constraints on the axial coupling constant, revealing its impact on scattering behavior. Under what conditions might such non-Hermitian effects become experimentally accessible, and what further insights could they provide into fundamental particle interactions?
Beyond the Boundaries of QED: A Necessary Deconstruction
Quantum electrodynamics, or QED, stands as one of the most successful theories in physics, precisely predicting interactions between light and matter. Its foundation lies in Hermitian quantum mechanics, ensuring probabilities remain normalized and physical predictions are stable. However, this very strength becomes a limitation when venturing beyond the well-established Standard Model of particle physics. Phenomena like certain particle decays, the behavior of open quantum systems, and the existence of exceptional states-those with properties not found in traditional physics-fall outside the scope of Hermitian QED. While remarkably accurate within its domain, the theory struggles to accommodate effects stemming from non-conservative interactions or systems where energy isn’t strictly preserved, necessitating the exploration of frameworks that extend or even supersede its current limitations to fully describe the universe’s complexities.
The pursuit of physics beyond the Standard Model increasingly necessitates exploration of non-Hermitian quantum mechanics. While standard quantum electrodynamics relies on Hermitian operators – ensuring probabilities remain real and conserved – this constraint limits the description of systems experiencing gain or loss, or those exhibiting decay and resonances. Non-Hermitian extensions, however, allow for complex-valued energies and wavefunctions, providing a framework to model open quantum systems and phenomena like exceptional points, where conventional quantum behavior breaks down. This approach isn’t merely a mathematical curiosity; it offers a potential pathway to describe unstable particles, decaying states, and interactions with the environment, potentially revealing new physics hidden within seemingly anomalous experimental results and offering insights into the nature of dark matter and other unsolved mysteries.
The persistent success of quantum electrodynamics (QED) belies an underlying rigidity when confronted with phenomena extending beyond well-established particle physics. Current theoretical models struggle to adequately describe interactions involving exotic states of matter, or those hinting at physics beyond the Standard Model, prompting a search for more adaptable frameworks. This necessitates a shift towards approaches capable of accommodating complexities absent in the traditional Hermitian formulation; a versatile system is required to model phenomena like parity-violating interactions or the behavior of particles with short lifetimes. Such advancements aren’t about replacing QED, but rather extending its capabilities, allowing physicists to probe the universe at its most fundamental level and potentially unlock a deeper understanding of reality.
Deconstructing Interactions: The Logic of Non-Hermitian QED
Non-Hermitian Quantum Electrodynamics (QED) represents a departure from standard QED by permitting the use of non-Hermitian operators in the Hamiltonian. This allows for the modification of fundamental particle interactions through the introduction of parameters such as the Axial Mass and Axial-Vector Coupling. The Axial Mass, typically denoted as m_A, introduces a mass term for axial-vector bosons, influencing their propagation and decay rates. Similarly, the Axial-Vector Coupling alters the strength of interactions involving axial-vector currents. These modifications are not simply mathematical extensions; they represent a potential mechanism for describing physics beyond the Standard Model, allowing for interactions that violate conventional constraints like CPT symmetry under specific parameter choices. The inclusion of these terms necessitates a re-evaluation of perturbative calculations and introduces novel phenomena not present in standard Hermitian QED.
Exceptional Points (EPs) arise in non-Hermitian Quantum Electrodynamics (QED) as specific parameter values where two or more eigenvalues of the Hamiltonian coalesce. This eigenvalue coalescence isn’t simply a quantitative change; it signifies a qualitative alteration in the system’s behavior, manifesting as a breakdown of the adiabatic theorem and a sensitivity to perturbations. At an EP, the eigenvectors associated with the coalescing eigenvalues also become indistinguishable, leading to a divergence of the system’s response to external stimuli. Mathematically, an EP is characterized by the vanishing of the gap between eigenvalues and the merging of corresponding eigenvectors; for a 2×2 Hamiltonian H , this occurs when the determinant of (H - \lambda I) and its trace both equal zero, at a specific value of λ. This sensitivity and qualitative change distinguish EPs from typical resonance phenomena and have implications for applications like enhanced sensing and novel device design.
PT-Symmetry, a crucial aspect of non-Hermitian Quantum Electrodynamics (QED), posits invariance under combined Parity (P) and Time-Reversal (T) transformations. This symmetry, when present, allows for a real energy spectrum despite the use of non-Hermitian Hamiltonians. The parameter space of non-Hermitian QED is constrained because maintaining PT-symmetry requires a specific relationship between the gain and loss terms introduced by the non-Hermitian operators. Specifically, the strength of the non-Hermitian terms must satisfy certain conditions to avoid spontaneous symmetry breaking and ensure the stability of the physical states. Deviations from these conditions result in complex eigenvalues, indicating instability and the breakdown of PT-symmetry; therefore, the search for and characterization of PT-symmetric regions within the parameter space is a central focus of research in this field.
The Thermal Universe: Modeling Interactions in a Heat Bath
Thermal Field Dynamics (TFD) addresses the limitations of standard perturbative calculations, which typically assume zero temperature, by providing a framework for computing scattering amplitudes at non-zero temperatures. This is critical for modeling physical systems where thermal effects are significant, such as high-energy heavy-ion collisions, the early universe, or stellar interiors. TFD accomplishes this by treating particles as existing within a thermal bath, where interactions are modified by the presence of thermally excited particles and antiparticles. The resulting amplitudes account for the contributions of all possible thermal states, offering a more accurate representation of scattering processes in realistic, finite-temperature environments. This formalism is particularly useful when dealing with systems where the temperature is comparable to, or exceeds, the mass scales of the participating particles, conditions under which standard perturbative approaches break down.
The Bogoliubov transformation is a canonical transformation used in thermal field dynamics to redefine the creation and annihilation operators for particles in a thermal bath. This transformation mixes these operators, generating new operators that diagonalize the Hamiltonian of the system at finite temperature. Specifically, it relates the original operators, b and b^{\dagger}, to new operators, β and \beta^{\dagger}, such that the new operators obey standard commutation relations. This process inherently incorporates the effects of thermal excitations by introducing contributions from both particles and holes, effectively accounting for the population of excited states at a given temperature and allowing for the calculation of observables in a thermally equilibrated system. The resulting expressions for the transformed operators include terms proportional to the thermal occupation number, dictated by distributions like the Bose-Einstein or Fermi-Dirac statistics, depending on the particle’s nature.
Thermal Field Dynamics employs the concept of a Thermal Vacuum, which represents the ground state of a quantum field at a non-zero temperature, differing from the standard vacuum state at zero temperature. Particle populations within this thermal vacuum are not determined by simple vacuum expectation values, but are instead described by statistical distributions dependent on particle statistics; fermions are governed by the Fermi-Dirac distribution f(E) = \frac{1}{e^{(E-\mu)/T} + 1}, while bosons follow the Bose-Einstein distribution f(E) = \frac{1}{e^{(E-\mu)/T} - 1}, where E is energy, μ is the chemical potential, and T is the temperature. These distributions dictate the average number of particles with a given energy at a specific temperature, directly impacting calculations of thermal correlation functions and scattering amplitudes.
Bhabha Scattering: A Precision Test of Theoretical Boundaries
Bhabha scattering, the process where electrons and positrons collide and scatter, provides a uniquely sensitive arena for probing the boundaries of quantum electrodynamics (QED). Unlike many other particle interactions, Bhabha scattering is readily calculable with high precision, establishing a stringent benchmark against which theoretical extensions can be tested. Specifically, investigations into non-Hermitian QED – a framework exploring physics beyond the standard Hermitian formulation – rely on comparing theoretical predictions for the scattering cross section with experimental observations. Deviations from standard QED predictions in Bhabha scattering would signal the presence of new physics governed by the non-Hermitian terms, potentially revealing previously unknown interactions or the influence of hidden dimensions. The inherent precision and clean signature of this interaction make it an ideal “test case” for validating or refuting theoretical models that venture beyond the well-established confines of conventional quantum field theory.
The theoretical prediction of Bhabha scattering relies on a robust framework of calculations stemming from Feynman diagrams and the scattering matrix, ultimately yielding the Bhabha scattering cross section – a precisely quantifiable value. This cross section represents the probability of electron-positron scattering at a given energy and angle, making it directly comparable to experimental observations. By meticulously calculating contributions from various Feynman diagrams, physicists can predict the expected scattering rate and then assess the validity of theoretical models against real-world data. Discrepancies between prediction and experiment would signal the need for refinements to the underlying theory, while strong agreement validates the model’s predictive power and provides confidence in its application to other physical phenomena. This process of theoretical prediction and experimental verification forms a cornerstone of high-energy physics research, allowing for increasingly precise tests of the Standard Model and the search for new physics beyond it.
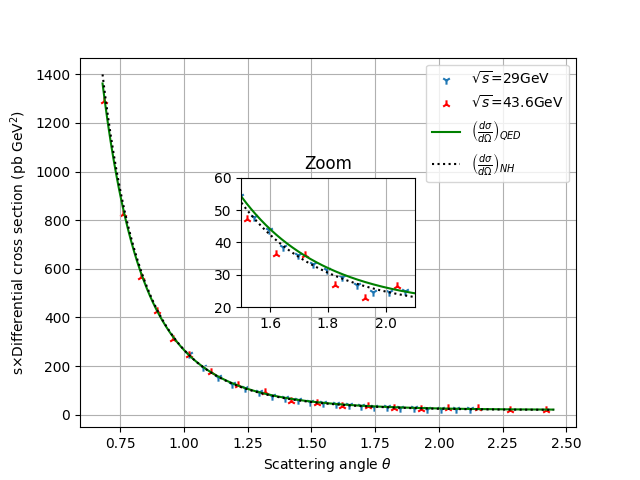
The precision of Bhabha scattering allows for rigorous constraints on theoretical parameters extending beyond the Standard Model. This work leverages the mathematical framework of Mandelstam variables – s, t, and u – to map the possible parameter space of non-Hermitian quantum electrodynamics. By meticulously calculating the scattering cross-section and comparing it to established experimental data, researchers have successfully placed an upper bound on the axial coupling constant, \alpha_a. The derived limit, approximately 1/5494, represents a significant refinement of existing constraints and provides a valuable benchmark for future investigations into physics beyond the Standard Model, demonstrating the power of precision measurements in particle physics.
The exploration of Bhabha scattering under non-Hermitian conditions represents a deliberate disruption of established quantum frameworks. This research doesn’t simply accept the existing rules; it actively probes their limits, seeking to understand where and how they break down under thermal influence. It’s akin to reverse-engineering the very fabric of particle interaction. As Marcus Aurelius observed, “Everything we hear is an echo of an unspoken thought.” This study isn’t merely calculating differential cross sections; it’s listening for the echoes of deeper principles, pushing against the boundaries of Quantum Field Theory to reveal the underlying structure, particularly how axial coupling parameters define the system’s stability and exceptional points.
Where Do We Go From Here?
The exploration of Bhabha scattering within a non-Hermitian framework reveals, predictably, that the universe isn’t quite as symmetrical as it pretends to be. The identification of bounds on axial coupling parameters, while valuable, merely delineates the edges of what remains unknown. A bug is the system confessing its design sins, and here, the ‘bug’ is the persistent tension between theoretical elegance and observed asymmetry. The insistence on Hermitian operators, for so long a bedrock of quantum field theory, now appears less a fundamental truth and more a convenient simplification.
Future work isn’t simply about refining these bounds, but interrogating the very assumptions that led to them. Thermal Field Dynamics, as employed here, offers a potent tool, but its limitations-particularly concerning the applicability of perturbative expansions at extreme temperatures-demand scrutiny. Exceptional points, those singularities where Hermitian symmetry breaks down, deserve a more thorough mapping; are they merely mathematical curiosities, or do they represent genuine physical instabilities within the scattering process?
The true challenge lies in constructing a more complete, inherently non-Hermitian quantum field theory. One that doesn’t treat asymmetry as an anomaly to be explained away, but as a fundamental aspect of reality. Perhaps, in dismantling the comfortable symmetry, a deeper understanding of the universe’s underlying architecture will emerge. Or, more likely, simply reveal a more complex set of rules to be broken.
Original article: https://arxiv.org/pdf/2602.15093.pdf
Contact the author: https://www.linkedin.com/in/avetisyan/
See also:
- Best Controller Settings for ARC Raiders
- How to Get to Heaven from Belfast soundtrack: All songs featured
- 10 Best Anime to Watch if You Miss Dragon Ball Super
- 10 Most Memorable Batman Covers
- Wife Swap: The Real Housewives Edition Trailer Is Pure Chaos
- Star Wars: Galactic Racer May Be 2026’s Best Substitute for WipEout on PS5
- The USDH Showdown: Who Will Claim the Crown of Hyperliquid’s Native Stablecoin? 🎉💰
- These Are the 10 Best Stephen King Movies of All Time
- Best X-Men Movies (September 2025)
- Netflix’s Stranger Things Replacement Reveals First Trailer (It’s Scarier Than Anything in the Upside Down)
2026-02-18 14:04