Beyond the Void: Entanglement’s Role in Vacuum Decay

Author: Denis Avetisyan

New research reveals how entanglement scales during the Sauter-Schwinger effect, a process where intense fields trigger pair creation from the quantum vacuum.

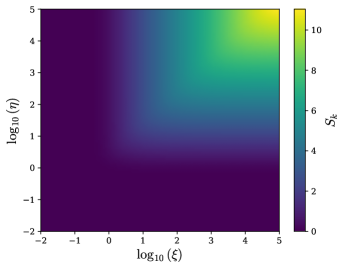
The study of the Sauter-Schwinger effect reveals a pairwise entanglement entropy <span class="katex-eq" data-katex-display="false">S_{\mathbf{k}}</span> that is particularly pronounced for the infrared mode <span class="katex-eq" data-katex-display="false">\omega_{\mathbf{k}}^{+}=\mu</span>, suggesting a fundamental link between vacuum decay and quantum correlations at low frequencies. — The study of the Sauter-Schwinger effect reveals a pairwise entanglement entropy $S_{\mathbf{k}}$ that is particularly pronounced for the infrared mode $\omega_{\mathbf{k}}^{+}=\mu$ , suggesting a fundamental link between vacuum decay and quantum correlations at low frequencies.

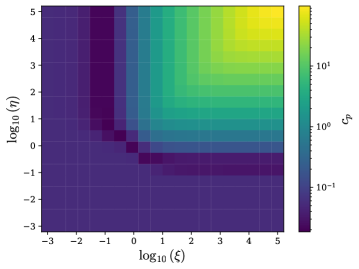
This study investigates the transition from area-law to volume-law scaling of entanglement entropy in scalar quantum electrodynamics during non-perturbative vacuum decay.

Quantum field theory predicts dramatic shifts in correlation structure during strong-field phenomena, yet quantifying these changes remains a significant challenge. This is addressed in ‘Entanglement scaling and dynamics in the Sauter-Schwinger effect’, where we present the first comprehensive numerical study of entanglement entropy-a powerful probe of quantum correlations-during non-perturbative pair creation. Our results demonstrate a transition from area-law to volume-law scaling of entanglement entropy for specific strong-field regimes, signaling a fundamental reorganization of quantum correlations induced by vacuum decay. How might these insights into entanglement scaling inform our understanding of other strongly correlated quantum systems and the emergence of spacetime itself?

Beyond Classical Correlations: Entanglement and the Fabric of Reality

Quantum correlations, far exceeding the bounds of classical physics, represent a cornerstone in the pursuit of fundamental understanding. These correlations are not simply a statement of shared information, but a deeply interwoven connection between quantum systems, even when separated by vast distances. The quantification of these correlations relies heavily on a measure called Entanglement Entropy, which moves beyond traditional correlation metrics to capture the uniquely quantum nature of these connections. By meticulously analyzing Entanglement Entropy, physicists gain critical insights into the underlying structure of quantum systems, paving the way for advancements in fields ranging from quantum computing to the very fabric of spacetime – offering a powerful lens through which to examine the mysteries of the universe and potentially reconcile quantum mechanics with general relativity.

Classical statistical methods, designed to analyze systems where parts are independent or weakly linked, prove inadequate when confronting the deeply interconnected nature of quantum systems. These traditional correlations, like simple covariance, fail to capture the non-local relationships inherent in entanglement – a phenomenon where two or more particles become linked in such a way that they share the same fate, no matter how far apart they are. Consequently, physicists have turned to novel analytical tools, such as entanglement entropy, to quantify these quantum correlations accurately. This shift isn’t merely a mathematical refinement; it represents a fundamental change in how correlations are understood, revealing that the interconnectedness of quantum systems is not just a matter of degree, but of a qualitatively different kind – one demanding entirely new frameworks for description and measurement. The inability of classical measures highlights the necessity of embracing the counterintuitive principles of quantum mechanics to fully grasp the behavior of matter at its most fundamental level.

The manner in which a quantum system’s entanglement scales with its size provides a profound window into the underlying structure of both spacetime and quantum field theories. Traditionally, entanglement entropy – a measure of this entanglement – has been predicted to follow an ‘Area Law’, where entanglement is proportional to the boundary surface area of the system, suggesting a holographic connection to gravity. However, certain quantum systems, particularly those exhibiting exotic phases of matter, can deviate from this law, displaying instead a ‘Volume Law’ where entanglement scales with the system’s volume. Recent findings demonstrate a measurable transition between these two regimes, revealing that entanglement doesn’t simply adhere to one law or the other, but rather undergoes a shift influenced by the system’s internal dynamics and dimensionality. This transition offers a novel approach to characterizing quantum phases of matter and exploring the emergence of spacetime geometry from quantum entanglement, potentially bridging the gap between quantum mechanics and general relativity through the lens of $\text{Entanglement Entropy}$ .

The entanglement entropy scales with system size according to a power law, as demonstrated by time evolution plots showing consistent behavior across varying subsystem sizes <span class="katex-eq" data-katex-display="false">R/20 < r < R/4</span> with parameters <span class="katex-eq" data-katex-display="false">\xi=10^2</span>, <span class="katex-eq" data-katex-display="false">\eta=10</span>, and <span class="katex-eq" data-katex-display="false">\tilde{\mu}=1</span> for a system of <span class="katex-eq" data-katex-display="false">N_{z}=100</span> and <span class="katex-eq" data-katex-display="false">N_{\varrho}=300</span>. — The entanglement entropy scales with system size according to a power law, as demonstrated by time evolution plots showing consistent behavior across varying subsystem sizes $R/20 < r < R/4$ with parameters $\xi=10^2$ , $\eta=10$ , and $\tilde{\mu}=1$ for a system of $N_{z}=100$ and $N_{\varrho}=300$ .

Gaussian States: A Tractable Window into Many-Body Quantum Systems

Multimode Gaussian states provide an analytically tractable framework for investigating many-body quantum systems due to their ability to be fully characterized by first-order and second-order moments. Unlike general quantum states which require exponentially increasing computational resources with system size, Gaussian states can be completely described by the covariance matrix, detailing the correlations between quadrature operators. This simplification enables efficient calculation of key quantum properties and allows for analytical progress in areas where exact solutions are otherwise inaccessible. The approach is particularly useful for bosonic systems, including those found in quantum optics and condensed matter physics, facilitating the study of entanglement, thermalization, and quantum phase transitions without resorting to computationally expensive numerical methods.

Multimode Gaussian states are fully characterized by the σ covariance matrix and the Wigner characteristic function χ. The covariance matrix, a real symmetric matrix, defines the variances and covariances of the quadrature amplitudes of the quantum field modes. Specifically, $\sigma_{ij} = \frac{1}{2} \langle x_i x_j + x_j x_i \rangle$ , where $x_i$ and $x_j$ are quadrature operators. The Wigner function χ is the Fourier transform of the density matrix in phase space and provides a quasi-probability distribution for the quadrature amplitudes; it uniquely determines all measurable quantities for the Gaussian state. Together, these two mathematical objects completely specify the quantum state and allow for the calculation of any relevant observable, circumventing the need to directly manipulate the typically intractable many-body wave function.

Multimode Gaussian states facilitate the efficient computation of entanglement entropy, enabling direct comparison between theoretical predictions and numerical simulations. Analysis within this framework demonstrates that entanglement entropy does not consistently follow the standard area-law scaling, $S \propto A$ , where $A$ represents the boundary area. Specifically, calculations reveal a variable power-law exponent and pre-factor characterizing the entanglement, indicating deviations from this established scaling behavior. These findings suggest a more nuanced relationship between boundary area and entanglement entropy in these systems, potentially driven by the specific characteristics of the Gaussian state and its constituent modes.

Analysis of the Sauter-Schwinger effect reveals a power-law scaling of final-state entanglement entropy with a pre-factor determined by parameters <span class="katex-eq" data-katex-display="false"> \tilde{\mu}=1 </span>, <span class="katex-eq" data-katex-display="false"> N_{z}=100 </span>, and <span class="katex-eq" data-katex-display="false"> N_{\varrho}=300 </span>, as demonstrated by fits with minimal error (<span class="katex-eq" data-katex-display="false"> \Delta p\sim 0.008 </span>) and high goodness of fit (<span class="katex-eq" data-katex-display="false"> R^{2}\sim 0.999 </span>). — Analysis of the Sauter-Schwinger effect reveals a power-law scaling of final-state entanglement entropy with a pre-factor determined by parameters $\tilde{\mu}=1$ , $N_{z}=100$ , and $N_{\varrho}=300$ , as demonstrated by fits with minimal error ( $\Delta p\sim 0.008$ ) and high goodness of fit ( $R^{2}\sim 0.999$ ).

The Sauter-Schwinger Effect: Witnessing Vacuum Instability

The Sauter-Schwinger effect describes a non-perturbative quantum electrodynamic (QED) process wherein a sufficiently strong electric field $\mathcal{E}$ can supply the energy required to create particle-antiparticle pairs from the vacuum. Unlike typical pair production involving high-energy photons interacting with matter, this process occurs even in empty space due to the inherent uncertainty principle and the field’s ability to virtualize particles. The predicted pair creation rate is exponential in the field strength and proportional to $\exp \left( -\frac{\pi m^2 c^3}{e \hbar \mathcal{E}} \right)$ , where $m$ is the particle mass, $c$ is the speed of light, $e$ is the elementary charge, and $\hbar$ is the reduced Planck constant. This rate becomes significant for electric fields approaching the Schwinger limit of approximately $1.3 \times 10^{18} \text{ V/m}$ .

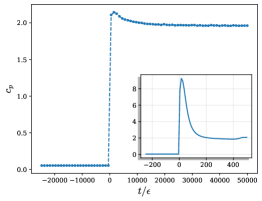
The Sauter-Schwinger effect is mathematically modeled using a complex scalar field, φ, evolving in time under the influence of an external, time-dependent electric field. This field is typically represented by a Sauter pulse, characterized by a time-dependent vector potential $A(t)[latex], allowing for the investigation of non-perturbative quantum electrodynamic effects. The Lagrangian density for this system includes a kinetic term, a mass term, and an interaction term coupling the scalar field to the vector potential, enabling the calculation of vacuum decay rates and particle production probabilities. The time-dependence of the Sauter pulse is crucial, as it drives transitions between the vacuum state and states containing particle-antiparticle pairs, ultimately describing the creation of real particles from seemingly empty space.</p> <p>The Adiabatic Approximation is crucial for calculating vacuum decay rates and particle production in strong electric fields because it allows for a simplified treatment of the time-dependent Schrödinger equation. This simplification reveals a notable shift in entanglement scaling: at low electric field strengths, entanglement between created particles scales with the boundary area - an ‘area-law’ - indicative of low-dimensional behavior. However, as the field strength increases, the entanglement transitions to a ‘volume-law’ scaling, demonstrating a distinctly three-dimensional behavior. This transition, occurring at specific field strengths approximately given by [latex]E_c \approx m^2/e$ , directly correlates with a significant increase in particle-antiparticle pair production rates, confirming the theoretical prediction of vacuum instability.

At a late time of <span class="katex-eq" data-katex-display="false">t/\tau = 10^{20}</span>, the correlation structure reveals nonlocal peaks in the strong-field regime, indicating pair creation via the Sauter-Schwinger effect with parameters <span class="katex-eq" data-katex-display="false">\tilde{\mu}=1</span> and <span class="katex-eq" data-katex-display="false">N\_{\varrho}=300</span>. — At a late time of $t/\tau = 10^{20}$ , the correlation structure reveals nonlocal peaks in the strong-field regime, indicating pair creation via the Sauter-Schwinger effect with parameters $\tilde{\mu}=1$ and $N\_{\varrho}=300$ .

Mathematical Tools: Deciphering the Language of Quantum Fields

The behavior of quantum fields, and consequently the particles they describe, is fundamentally dictated by the Klein-Gordon equation. This equation, a relativistic wave equation, extends the Schrödinger equation to encompass particles that lack mass, such as photons, and accurately predicts their dynamic evolution in spacetime. It posits that particles aren't simply points, but excitations of an underlying field, and the equation governs how these excitations propagate and interact. Solutions to the Klein-Gordon equation, represented by $\left(\partial_{\mu}\partial^{\mu}+m^{2}\right)\phi(x) = 0$ , where $\phi(x)$ represents the field and $m$ is the particle’s mass, define the possible states of the field and, crucially, determine the probabilities associated with detecting a particle at a given point in space and time. This equation, therefore, serves as the cornerstone for understanding the quantum mechanical behavior of bosons and provides a crucial link between quantum field theory and the observed properties of fundamental particles.

The analysis of quantum fields exhibiting cylindrical symmetry-fields that remain unchanged under rotations around a central axis-is significantly streamlined through the application of cylindrical coordinates. This mathematical system, employing coordinates $(\rho, \phi, z)$ representing radial distance, angular position, and axial height respectively, allows for the separation of variables within the field equation. Consequently, a complex problem is reduced to a set of more manageable, independent equations, each dependent on a single coordinate. This simplification isn’t merely computational; it reveals inherent symmetries within the field itself, enabling physicists to more easily identify conserved quantities and understand the field’s behavior. By leveraging the inherent geometry of cylindrical symmetry, calculations become tractable and physical insights are more readily accessible, offering a powerful tool for investigating phenomena like the behavior of particles confined to cylindrical potentials or fields propagating along cylindrical waveguides.

Quantum fields, despite their abstract nature, aren't simply undefined spaces; they are described by solutions to field equations known as mode functions. These functions represent the fundamental building blocks of the field, each corresponding to a distinct possible state of a particle. Much like the different vibrational modes of a guitar string each produce a unique sound, each mode function describes a specific energy and momentum configuration for the quantum field. The complete field is then understood as a superposition of these modes, with the amplitude of each mode determining the probability of observing a particle in that particular state. Mathematically, these mode functions often take the form of plane waves or cylindrical waves - for example, $e^{ik \cdot x}$ - and their properties dictate how particles propagate and interact, ultimately shaping the observable universe at the smallest scales. Therefore, understanding mode functions is crucial to deciphering the behavior of quantum fields and the particles they embody.

A conventional lattice regularization in cylindrical coordinates is dimensionally reduced to an effective <span class="katex-eq" data-katex-display="false">1+1</span>-dimensional lattice theory. — A conventional lattice regularization in cylindrical coordinates is dimensionally reduced to an effective $1+1$ -dimensional lattice theory.

Spatial Partitioning: Dissecting Quantum Systems to Reveal Entanglement

Spatial bipartition represents a cornerstone in the study of quantum many-body systems, offering a method to dissect a complex system into spatially separated subsystems. This technique involves defining a dividing surface within the system, effectively creating two distinct regions and allowing researchers to analyze the correlations between these regions rather than treating the system as a monolithic whole. The principle isn't merely about division; it’s a pathway to understanding entanglement - a uniquely quantum phenomenon - by quantifying how much information about one region is linked to the other. This approach is crucial because many physical properties, such as conductivity or magnetic behavior, emerge from these internal correlations, and spatial bipartition provides a framework to rigorously examine them. Through this partitioning, researchers can then apply concepts like entanglement entropy to measure the degree of quantum connectedness and, ultimately, gain insights into the system’s overall behavior and emergent properties.

Spatial bipartition, while defining how a quantum system is divided, gains analytical power when integrated with the formalism of Gaussian states and the concept of Entanglement Entropy. This combination provides a robust method for quantifying the correlations existing between the resulting subsystems. By characterizing the entanglement-a uniquely quantum form of correlation-across the partition, researchers can move beyond simply knowing a system is divided to precisely measuring the strength and nature of the connections remaining between its parts. The resulting entanglement entropy, often expressed as $S = -Tr(\rho \log \rho)$ , serves as a direct indicator of these correlations; changes in this value reveal how strongly the subsystems remain linked, even when spatially separated, and provide insights into the system’s overall quantum behavior.

A refined approach to spatial partitioning involves decomposing the quantum field into real and imaginary components, a technique that enables the application of quadrature operators for a more nuanced investigation of entanglement. This methodology reveals a strong link between the scaling behavior of entanglement entropy - specifically, the transition from area-law to volume-law scaling - and the onset of substantial particle-antiparticle pair creation. The study demonstrates that this shift in scaling is not merely a topological change, but is directly quantifiable through alterations in the pre-factor governing the entanglement scaling; a larger pre-factor consistently correlates with regimes where pair production is dominant, providing a precise measure of how correlations restructure as particles emerge from the vacuum. This connection offers a pathway to utilize entanglement entropy as a diagnostic tool for probing the dynamics of particle creation in quantum field theory.

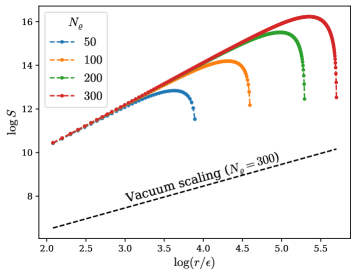
Entanglement entropy scales with system size <span class="katex-eq" data-katex-display="false">N_{\varrho}</span> in both the initial vacuum state and the late-time state (<span class="katex-eq" data-katex-display="false">t/\tau = 10^{20}</span>) for <span class="katex-eq" data-katex-display="false">\xi = 10^2</span> and <span class="katex-eq" data-katex-display="false">\eta = 10</span>, revealing consistent subsystem scaling behavior. — Entanglement entropy scales with system size $N_{\varrho}$ in both the initial vacuum state and the late-time state ( $t/\tau = 10^{20}$ ) for $\xi = 10^2$ and $\eta = 10$ , revealing consistent subsystem scaling behavior.

The study meticulously charts entanglement scaling during vacuum decay, revealing a shift from area to volume law under specific conditions. This mirrors a fundamental tension in understanding complex systems-the desire for simple explanations versus the reality of interwoven dependencies. As Jean-Jacques Rousseau observed, “The more we are connected, the more we are free.” The research demonstrates that while initial entanglement appears constrained by spatial boundaries (area law), increasing particle creation loosens those constraints, leading to a more pervasive, volume-dependent entanglement. This isn't simply about predicting particle behavior; it's acknowledging that predictive power is not causality, and the observed entanglement is a consequence of the dynamic interplay between quantum fields, not a predetermined outcome. The work emphasizes that discerning genuine connections requires rigorous analysis, lest one mistake correlation for causation-a point Rousseau would likely appreciate.

Where Does This Leave Us?

The observation of entanglement transitioning from area to volume scaling in the Sauter-Schwinger effect isn’t a destination, but a particularly clear signpost. It confirms that entanglement entropy, despite its computational challenges, continues to be a reliable, if demanding, probe of quantum field dynamics - particularly when those dynamics veer from the perturbative regime. The real work, predictably, lies in understanding why this transition occurs under specific conditions, and what that implies about the fundamental geometry of vacuum decay. This isn’t about finding the ‘right’ scaling law, but about meticulously mapping the errors in its application.

Future investigations should focus on extending these calculations beyond the simplified scenarios typically employed. Realistically, the clean Gaussian states utilized here are an approximation. The impact of interactions, and the resulting deviations from Gaussianity, remains largely unexplored. More importantly, the connection between this geometric entanglement and the detectability of pair creation-a tangible physical signature-requires significant refinement. A scaling law is merely a mathematical curiosity without a pathway to experimental verification.

Ultimately, the value of this line of inquiry isn’t in predicting the rate of vacuum decay-that remains a daunting task. It’s in forcing a confrontation with the limitations of current calculational techniques, and acknowledging that wisdom, in this context, is knowing precisely where the covariance matrix fails to represent reality. The most fruitful progress will likely come from embracing those failures, not smoothing over them.

Original article: https://arxiv.org/pdf/2601.14390.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/