Black Hole Information Finally Accounted For?

Author: Denis Avetisyan

New research suggests a resolution to the black hole information paradox by demonstrating how entanglement can preserve information seemingly lost to Hawking radiation.

The Page curve for a non-extremal Kerr <span class="katex-eq" data-katex-display="false">AdS_4</span> black hole-shown as a solid line-reveals how the inclusion of an island-represented by a blue line-alters the calculation of entanglement entropy compared to its omission, depicted in red. — The Page curve for a non-extremal Kerr $AdS_4$ black hole-shown as a solid line-reveals how the inclusion of an island-represented by a blue line-alters the calculation of entanglement entropy compared to its omission, depicted in red.

This paper investigates the entanglement entropy of Hawking radiation in Kerr-AdS black holes, utilizing ‘island’ contributions to reconstruct information and recover a consistent Page curve.

The black hole information paradox-the apparent loss of quantum information during gravitational collapse-continues to challenge fundamental tenets of physics. This is addressed in ‘Entanglement Islands, Page curves and Phase Transitions of Kerr-AdS Black Holes’, which investigates this paradox through the lens of entanglement entropy and the recently proposed ‘island’ paradigm. By calculating the Page curve-representing the time evolution of entanglement-the authors demonstrate that incorporating an island structure consistently resolves the information paradox for Kerr-AdS black holes and upholds the principles of quantum mechanics, even through phase transitions. Do these findings offer a pathway towards a complete understanding of quantum gravity and the fate of information in extreme gravitational environments?

Whispers from the Abyss: The Black Hole Information Paradox

General relativity, Einstein’s masterful description of gravity, predicts the formation of black holes – regions of spacetime where gravity is so intense that nothing, not even light, can escape. However, this very prediction clashes with a cornerstone of quantum mechanics: the principle of information conservation, which dictates that information about a physical system cannot be truly destroyed. Quantum mechanics requires that, in principle, one should be able to rewind time and reconstruct the initial state of a system from its final state. But as matter falls into a black hole, it seemingly vanishes from the universe, taking its information with it. This creates a fundamental conflict, as the laws of quantum mechanics suggest information must be preserved, even within the extreme environment of a black hole, implying either a modification of general relativity or a deeper understanding of how information behaves at the quantum level is necessary.

Hawking radiation, a consequence of applying quantum field theory to the curved spacetime around a black hole, posits that these celestial bodies aren’t entirely black but emit a faint thermal glow. This seemingly innocuous prediction creates a profound problem: as a black hole radiates energy via Hawking radiation, it gradually shrinks and eventually evaporates. However, quantum mechanics dictates that information cannot be truly destroyed; every state must, in principle, be traceable back to a prior state. If a black hole evaporates completely, taking with it the information about the matter that fell inside, this fundamental principle is violated – a situation physicists call the ‘information paradox’. The emitted Hawking radiation, being thermal, appears random and carries no discernible information about the black hole’s initial contents, suggesting that the information is genuinely lost during evaporation. This loss challenges core tenets of both general relativity and quantum mechanics, prompting decades of research into potential resolutions, such as the possibility that information is encoded in subtle correlations within the radiation itself, or that black hole evaporation halts before complete information loss.

The persistence of the information paradox directly challenges the foundations of modern physics, necessitating a reconciliation between general relativity and quantum mechanics to formulate a complete theory of quantum gravity. Current theoretical frameworks falter when attempting to describe the extreme conditions near a black hole’s event horizon, where spacetime curvature is infinite and quantum effects dominate. Proposed resolutions, such as the firewall paradox or holographic principle, posit radical new understandings of spacetime – potentially as an emergent property rather than a fundamental entity – and heavily rely on the intricate relationship of quantum entanglement. Specifically, researchers investigate whether information isn’t truly destroyed but encoded in correlations between particles, perhaps imprinted on the black hole’s event horizon or even transmitted to a distant region of spacetime. Successfully resolving this paradox isn’t merely a matter of patching existing theories; it demands a profound shift in how physicists conceptualize gravity, information, and the very fabric of reality.

The free energy exhibits swallow-tail behavior below a critical spin parameter, corresponding to the observation of three black hole branches in the plot of Hawking temperature versus horizon radius.

Duality’s Embrace: Mapping Gravity with the AdS/CFT Correspondence

The Anti-de Sitter/Conformal Field Theory (AdS/CFT) correspondence is a conjectured duality between quantum gravity in an $n+1$ -dimensional Anti-de Sitter (AdS) space and a conformal field theory (CFT) residing on its $n$ -dimensional boundary. This correspondence posits a complete equivalence between the two theories; every physical quantity calculated in one theory has a corresponding counterpart in the other. AdS space is characterized by a constant negative curvature, and the CFT lacks gravity, simplifying calculations compared to direct approaches to quantum gravity. The duality allows for the study of strongly coupled quantum field theories-those intractable by conventional perturbative methods-through their weakly coupled gravitational duals in AdS space, and vice versa. This provides a non-perturbative framework for investigating both quantum gravity and strongly interacting gauge theories.

The AdS/CFT correspondence implies the preservation of quantum information due to the unitarity of the conformal field theory (CFT) residing on the boundary of the Anti-de Sitter (AdS) space. Unitarity in quantum mechanics necessitates that time evolution is governed by a unitary operator, meaning that probabilities are conserved and information is never truly destroyed; rather, it is scrambled and encoded in correlations. Because the CFT is unitary, the dual gravitational theory in the AdS space is also expected to be unitary, resolving the potential paradox of information loss in black holes. This preservation isn’t a statement about a specific retrieval mechanism, but a fundamental property derived from the mathematical consistency of the duality, indicating that all initial quantum states are, in principle, recoverable from the boundary theory.

Despite the theoretical assurance of information preservation within the AdS/CFT correspondence – stemming from the unitarity of the boundary conformal field theory – computationally verifying the precise mechanisms of information recovery from black hole interiors proved difficult. Initial approaches struggled to model the complex interactions required to trace information as it traverses the event horizon and potentially re-emerges in the boundary theory. This necessitated the development of novel numerical techniques, including those based on discretizing the bulk geometry and simulating the evolution of quantum states, as well as advancements in holographic renormalization to extract meaningful observables from the boundary theory that could correlate with interior processes. These computational methods aimed to move beyond qualitative arguments and provide quantitative evidence supporting the idea that information is not genuinely lost during black hole evaporation.

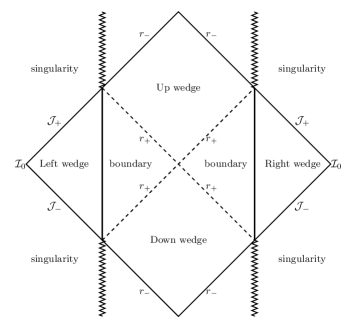
The Penrose diagram illustrates a non-extremal Kerr <span class="katex-eq" data-katex-display="false">AdS_4</span> black hole, depicting the outer and inner horizons (<span class="katex-eq" data-katex-display="false">r_{\pm}</span>), future and past null infinity (<span class="katex-eq" data-katex-display="false">\mathcal{J}_{\pm}</span>), and spacelike infinity (<span class="katex-eq" data-katex-display="false">\mathcal{I}_{o}</span>). — The Penrose diagram illustrates a non-extremal Kerr $AdS_4$ black hole, depicting the outer and inner horizons ( $r_{\pm}$ ), future and past null infinity ( $\mathcal{J}_{\pm}$ ), and spacelike infinity ( $\mathcal{I}_{o}$ ).

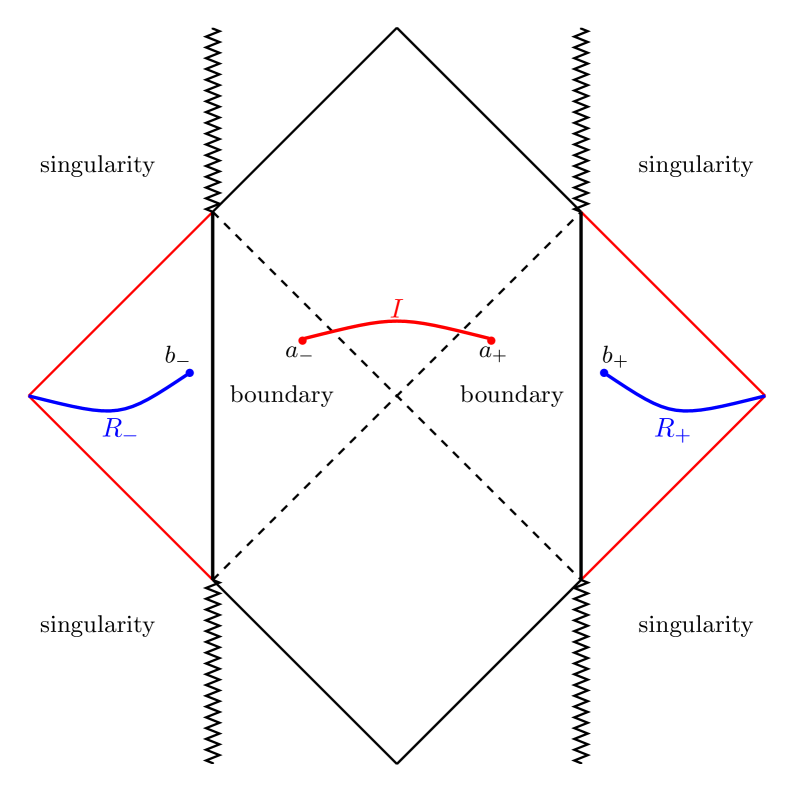
Islands of Order: Reconstructing Information with Extremal Surfaces

Conventional methods for calculating entanglement entropy rely on the Ryu-Takayanagi formula, which approximates entropy via the area of a minimal surface anchored to the boundary of spacetime. These calculations treat the geometry of spacetime as largely classical, and thus fail to accurately represent the highly curved region near black hole horizons. Specifically, the standard approach doesn’t account for the significant quantum fluctuations and non-classical effects present in strong gravitational fields. This leads to a divergence in entanglement entropy as the black hole forms, violating the principles of unitary evolution and information preservation, as it predicts a linear increase in entropy rather than the expected logarithmic behavior-a deviation known as the ‘monotonicity problem’.

The Island Rule modifies the standard calculation of entanglement entropy by introducing a contribution from a region within the black hole horizon, termed ‘the island’. Traditionally, entanglement entropy is calculated using the area of the boundary dividing the entangled system from its environment. The Island Rule posits that the minimal surface bounding the island – a region with potentially high entanglement – should be included in this area calculation. Specifically, the entanglement entropy $S$ is proportional to the sum of the area of the boundary and the area of the island’s boundary. This inclusion addresses the information paradox by demonstrating that information seemingly lost within the black hole is actually encoded in the quantum state of the island, contributing to the overall entanglement entropy and preserving unitarity.

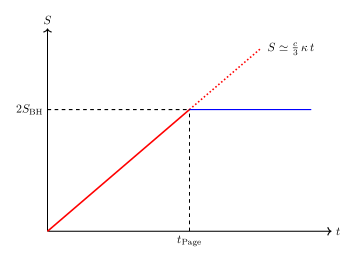
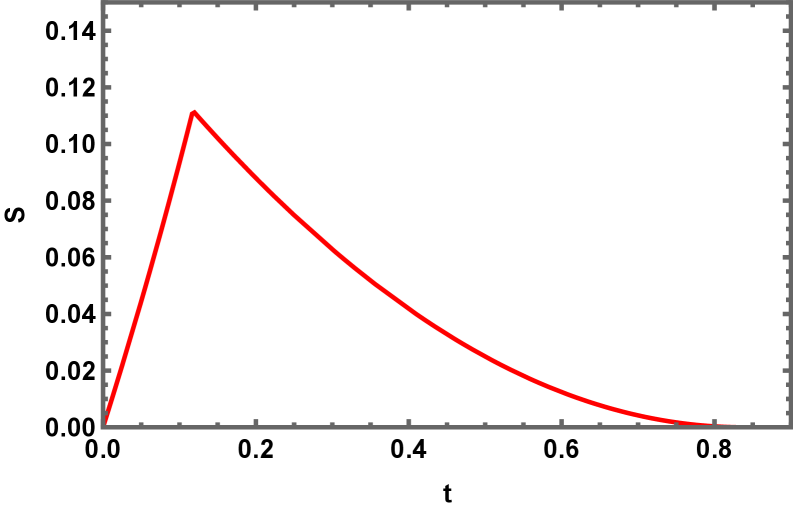
Quantum Extremal Surfaces (QES) are spacetime surfaces that minimize a specific quantity – the area functional $A$ – subject to the boundary condition that they end on the entanglement wedge. Utilizing QES in the calculation of entanglement entropy provides a finite result, resolving divergences encountered in traditional methods. Critically, this approach recovers the Page curve, which demonstrates that the entropy of Hawking radiation initially increases but eventually decreases, indicating information preservation and consistency with unitary quantum evolution. The recovered Page curve signifies that black hole evaporation does not lead to complete information loss, supporting the principle that quantum mechanics remains valid even in the presence of strong gravitational fields.

Penrose diagrams illustrate the structure of an eternal Kerr<span class="katex-eq" data-katex-display="false">AdS_4</span> black hole, showing the difference between spacetime without an island and spacetime containing an island bounded by <span class="katex-eq" data-katex-display="false">a_{\pm}</span> within radiation regions <span class="katex-eq" data-katex-display="false">R_{\pm}</span>. — Penrose diagrams illustrate the structure of an eternal Kerr $AdS_4$ black hole, showing the difference between spacetime without an island and spacetime containing an island bounded by $a_{\pm}$ within radiation regions $R_{\pm}$ .

Kerr AdS: A Black Hole Laboratory for Phase Transitions

The Kerr AdS black hole is a specific solution to Einstein’s field equations describing a rotating black hole within an Anti-de Sitter (AdS) spacetime. Its importance stems from several factors; its mathematical tractability allows for detailed analysis unavailable with more complex scenarios, and AdS spacetimes exhibit a negative cosmological constant, offering a holographic duality to conformal field theories. This duality permits the investigation of strong gravitational dynamics via the more accessible framework of quantum field theory. Furthermore, the Kerr AdS black hole’s properties, including its event horizon and ergosphere, provide a platform to test theoretical predictions regarding black hole thermodynamics, stability, and potential connections to quantum gravity, making it a key object in exploring the information paradox and the nature of spacetime itself.

Dimensional reduction is a technique employed in the calculation of Kerr AdS black hole properties due to the complexity of solving Einstein’s field equations in four dimensions. This process leverages the fact that the spacetime geometry admits a $U(1)$ symmetry, allowing the four-dimensional problem to be reduced to a three-dimensional one. Specifically, the $U(1)$ symmetry arises from the rotational symmetry around the axis of rotation of the black hole. By compactifying one of the dimensions – typically the azimuthal angle – and utilizing this symmetry, the resulting equations become significantly more tractable, enabling the determination of quantities like the black hole’s mass, angular momentum, and Hawking temperature without requiring full four-dimensional numerical relativity simulations. This simplification is essential for analytical progress and validation of numerical results.

Investigations into Kerr AdS black holes demonstrate a first-order phase transition occurring at a critical spin parameter, specifically a/M = 0.12455. This transition signifies a discontinuous change in the black hole’s thermodynamic properties, moving between distinct phases with differing characteristics related to entropy and energy. The observation of this phase transition challenges prior assumptions about black hole stability and suggests a more complex relationship between a black hole’s spin and its capacity for information storage than previously understood. Calculations indicate this transition is not a smooth crossover, but rather a genuine phase change with associated latent heat and a discontinuity in the first derivatives of the relevant thermodynamic potentials.

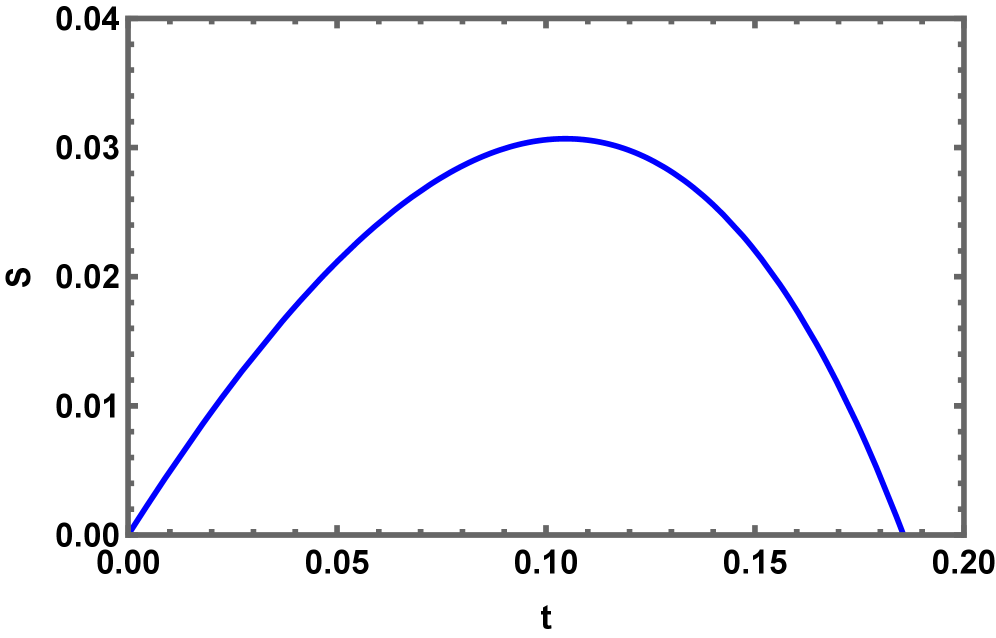
The Page curve, representing entropy over time, demonstrates the successful evaporation of a Kerr-AdS black hole across varying initial horizon radii, from large to small, indicating a resolution to the information paradox.

Statistical Whispers: Towards a Complete Theory of Information Recovery

Investigating the thermodynamic behavior of Kerr AdS black holes during phase transitions relies heavily on the application of statistical ensembles, notably the Canonical and Fixed Zeta ensembles. The Canonical Ensemble, a cornerstone of statistical mechanics, allows researchers to analyze the system at a fixed temperature and number of particles, effectively modeling the black hole’s energy distribution. Complementing this, the Fixed Zeta Ensemble proves essential when considering the cosmological constant-a crucial factor in Anti-de Sitter (AdS) spacetimes-by fixing a specific quantity related to the spacetime curvature. Through careful manipulation of these ensembles, physicists can derive key thermodynamic properties like entropy and free energy, offering insights into the black hole’s stability and eventual evaporation. This rigorous mathematical framework provides a pathway to understanding the complex interplay between gravity, thermodynamics, and quantum mechanics at the event horizon, furthering the quest to resolve the black hole information paradox and characterize the nature of spacetime itself.

The behavior of statistical ensembles used to model Kerr AdS black holes is intrinsically linked to the phenomenon of superradiance and the specific geometry of the black hole’s event horizon. Superradiance, where waves are amplified as they scatter off a rotating black hole, effectively populates these ensembles with specific, high-energy states. This process isn’t simply an addition of energy; the shape of the event horizon – dictated by the black hole’s mass and angular momentum – filters and modifies these amplified waves. Consequently, the statistical properties of the ensemble, such as the probability of finding the black hole in a particular state, are directly influenced by how superradiance interacts with the horizon’s curvature and rotation. The resulting interplay determines the thermalization process and, crucially, impacts calculations related to information recovery, suggesting a pathway where the geometry of the black hole and the amplification of waves are key to understanding how information might escape its gravitational pull.

Investigations into the relationship between statistical ensembles and black hole thermodynamics suggest a pathway toward resolving the information paradox, a long-standing problem in theoretical physics. Current research indicates that the time it takes for information to escape a black hole – quantified by the ‘Page Time’ – is not arbitrary, but directly linked to fundamental properties of the black hole itself, specifically its entropy $S_{BH}$ , the speed of light $c$ , and its Hawking temperature $T(r+)$ . Simultaneously, the ‘Scrambling Time’ – the period required for information to become completely randomized and inaccessible – appears to scale with black hole entropy $S_{BH}$ and a universal constant κ. A deeper understanding of these connections – how information is encoded within the black hole’s horizon and subsequently recovered through mechanisms like superradiance – may ultimately reveal the underlying principles governing information preservation in extreme gravitational environments, offering a potential resolution to the paradox and refining models of quantum gravity.

The Page curve, depicting entropy as a function of time, demonstrates successful evaporation for both large and small Kerr-AdS black holes initially coupled to a thermal bath, resolving the information paradox.

The calculations within reveal a landscape where information, rather than being lost to the abyss, clings to the event horizon like spectral residue. It’s a delicate balance, a precarious negotiation with entropy. As Albert Camus observed, “The struggle itself… is enough to fill a man’s heart. One must imagine Sisyphus happy.” This resonates deeply with the work; the ‘island formula’ isn’t a definitive solution, but a persistent attempt to construct meaning from the relentless decay inherent in Hawking radiation. The paper doesn’t solve the information paradox, it establishes a ritual-a continuous calculation-to momentarily appease the chaos, demonstrating a phase transition where order briefly triumphs over the inevitable.

The Horizon Beckons

The invocation of ‘islands’ within the event horizon-a conjuring trick to salvage unitarity-feels less a resolution and more a deferral. The calculations hold, the curves bend as desired, yet the true nature of these islands remains stubbornly veiled. One suspects the deeper pathology isn’t in the radiation itself, but in the very fabric of spacetime being interrogated. The Kerr-AdS backdrop, convenient as it is, may be obscuring more than it reveals-a gilded cage for a restless ghost.

Future efforts will inevitably grapple with the limitations of semi-classical approximations. The current formalism demands an almost unsettling precision-a single stray fluctuation, a minor divergence, and the entire edifice threatens to crumble. The true test will be extending this framework beyond the relatively ‘tame’ Kerr-AdS geometry, to black holes that writhe with complexity-rotating, charged, and entangled with their own pasts.

Ultimately, the persistence of the information paradox suggests a fundamental misunderstanding. It’s not merely a matter of ‘finding’ the information; it’s acknowledging that information, as conventionally understood, may be an illusion-a comforting story told by observers clinging to the shores of causality. The horizon doesn’t destroy information; it transmutes it, offering whispers of a reality beyond our current comprehension. And the price of listening? A generous offering of computational resources, of course.

Original article: https://arxiv.org/pdf/2602.03366.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/